Wilcoxon符号秩检验不仅可以用于单个样本的中位数与总体中位数的比较,也可以用于成对样本差值的中位数与0的比较。配对样本的Wilcoxon符号秩检验的目的是推断配对样本之间的差值的总体中位数是否不同于0,即推断配对的两个相关样本来自的两个总体中位数是否存在差异。本文将结合实例介绍配对样本Wilcoxon符号秩检验的适用条件和假设检验理论。
适用条件
对于配对设计的连续性变量,可以选择配对t检验或Wilcoxon符号秩检验。配对t检验适用于两组差异近似正态分布的数据。当不满足此条件时(个人认为样本量太小时一般不满足),可选择Wilcoxon符号秩检验。配对设计有序分类变量的比较应采用Wilcoxon符号秩检验。当使用Wilcoxon符号秩检验时,需要满足三个条件:
观察变量为连续变量或有序分类变量。
观察变量可分为2组。
观测变量的数据结构为配对形式。
统计量计算
配对设计的有序分类变量的比较
Wilcoxon符号秩检验用于配对的等级资料,需要先将等级从弱到强转换为秩(1,2,3,…);然后计算每对秩的差值,省略所有差值为0的对,使所有剩余有效对为n,最后根据n个差值编译正负秩,并计算正负秩和。
现在要研究电刺激对于中风患者的大脑皮层的影响,想看电刺激前后患者的某一指标是否发生了显著的变化。
一共招募了9名受试者,分别记录了电刺激前后患者大脑的生理指标,我们分别用ESbefore和ESafter表示。
电刺激试验的间隔时间适中,收集的部分数据如下。
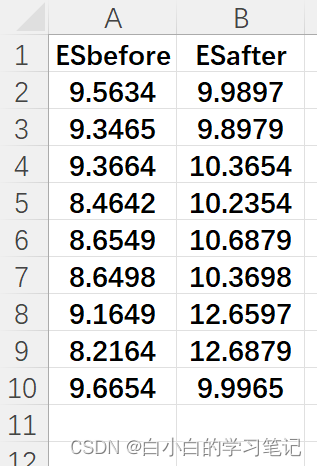
我们将数据导入SPSS

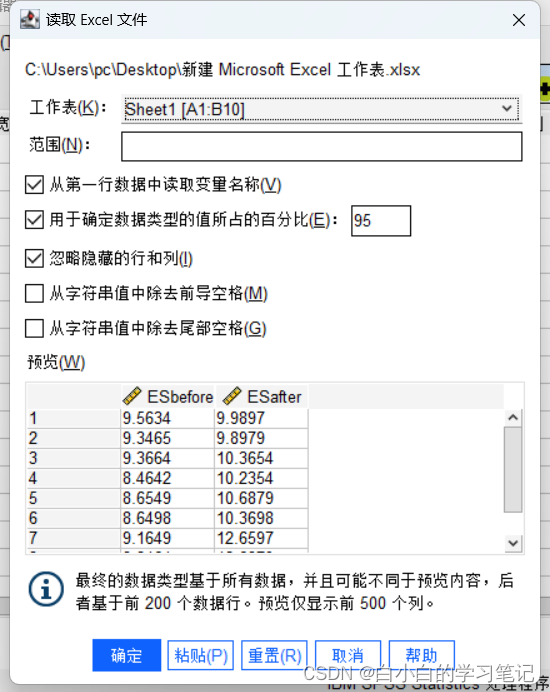
点击确认即可,导入之后我们可以看到

接下来我们点击分析,选择非参数检验中的相关样本(配对就是相关样本,非配对就是独立样本)

选择定制分析

导入我们的两个字段,分别是ESbefore和ESafter

选择定制检验,勾选威尔科克森匹配对符号秩检验,点击运行

这里是我们最关键的结果

我们得到的显著性为0.008<0.05,所以拒绝原假设(无差异),原假设发生的可能性太小了,样本前后差异性显著,有统计学意义

























 480
480

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










