【DOE】--方差、自由度、回归分析

系列文章目录

---

前言

一、假设检验

1.定义

对总体参数分布做假设，根据样本Sample观测值运用统计学技术分析方法检验这种假设是否正确，从而选择接受或拒绝假设的过程。

2.假设检验的类别

假设检验类别	minitab运用	条件和解决的问题
Z检验	1-Sample Z	已知总体u和G，检验单样本均值与总体u是否相同
t检验	1-Samplet	已知总体，末知总体G，检验单个样本均值与总体均值差异
	2-Sample t	检验两个样本均值之间差异
	Pairedt	比较数据成对时的两个总体平均值的差异。
F检验	2Variance	两个总体分布的方差检验
Barlett检验	Test for Equal Variance	样本数据为正态分布的多样木方差检验
Levene检验	Test for Equal Variance	样本数据为非正态分布的多样本方差检验
比例检验	1Proportion 2Proportion

3.假设检验的步骤

• 建立对立假设和原假设
• 选择显著性水平（一般为5%）
• 选择检验方法
• 计算关于样本的Data的P值
• 比较P值和显著性水平导出结论

二、方差分析

1.定义

·方差分析（Analysis of Variance，简称ANOVA），又称“变异数分析"，或“F检验"，是R.A.Fisher发明的，用于两个及两个以上样本均数差别的显著性检验。
·方差分析是要检验各个水平的均值是否相等，采用的方法是比较各水平的方差。

方差分析（Analysis of Variance，缩写为ANOVA）是数理统计学中常用的数据处理方法之一，是工农业生产和科学研究中分析试验数据的一种有效的工具。也是开展试验设计、参数设计和容差设计的数学基础。
一个复杂的事物，其中往往有许多因素互相制约又互相依存。方差分析的目的是通过数据分析找出对该事物有显著影响的因素，各因素之间的交互作用，以及显著影响因素的最佳水平等。
方差分析是在可比较的数组中，把数据间的总的“变差”按各指定的变差来源进行分解的一种技术。对变差的度量，采用离差平方和。方差分析方法就是从总离差平方和分解出可追溯到指定来源的部分离差平方和。这是一个很重要的思想。
回归分析（Regression Analysis）是研究一个变量Y与其它若干变量X之间相关关系的一种数学工具，它是在一组试验或观测数据的基础上，寻找被随机性掩盖了的变量之间的依存关系。粗略地讲，可以理解为用一种确定的函数关系去近似代替比较复杂的相关关系，这个函数称为回归函数，在实际问题中称为经验公式。回归分析所研究的主要问题就是如何利用变量X，Y的观察值（样本），对回归函数进行统计推断，包括对它进行估计及检验与它有关的假设等。

2.方差的引入

观察值之间的差异包括系统性差异和随机性差异
方差分析实际上是用来辨别各水平间的差别是否超出了水平内正常误差的程度

• F统计量
  水平间（也称组间）方差和水平内（也称组内）方差之比是一个统计量。实践证明这个统计量遵从一个特定的分布，数理统计上把这个分布称为F分布。
  F=组间方差/组内方差
  组间方差（SSB）+组内方差（SSw）=总方差（SST）
• F分布的特征
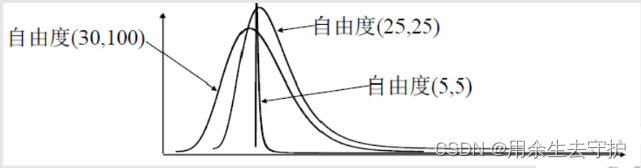
  ·从F分布的式子看出，F分布的形状由分母和分子两个变量的自由度确定，因此F分布有两个参数。
  ·F分布的曲线为偏态形式，它的尾端以横轴为渐近线趋于无穷。

• 方差分析的前提
  ·不同组样本的方差应相等或至少很接近在方差分析之前，我们可利用Minitab对数据作方差一致性检验

3.方差的计算

《》

4.失拟

JMP网站-失拟
“失拟”报表可为评估模型是否良好拟合数据的检验提供详细信息。仅当可以执行该检验时才会显示“失拟”报表。该检验依赖于使用独立于模型的估计值估计响应方差的能力。构造该估计值要求模型效应的重复值处有响应值。该检验涉及纯误差估计值的计算，它基于利用这些重复观测得到的平方和。
在以下情况下，由于无法计算检验统计量，“失拟”报表不会显示：
X 变量没有重复点，所以无法计算纯误差平方和。
模型饱和，这表示估计参数的个数与观测数相同。这种模型完全拟合，所以不可能评估失拟。
模型中的误差平方和与纯误差平方和之间的差值称为失拟平方和。若模型不合适，失拟变异会显著大于纯误差变异。例如，您的预测变量的函数形式可能有误，或是您模型中的交互作用效应可能不足或不正确。
“失拟”报表包含以下列：
源
列出变异的三个来源：失拟、纯误差和总误差。
自由度
记录每个误差源的自由度：

• 总误差的自由度与“方差分析”表的“误差”行中的自由度值相同。根据平方和分解，总误差自由度可分为失拟自由度和纯误差自由度
• 纯误差自由度是每个重复观测组的合并结果。通常情况下，若有 g 个组，每组中每个效应具有相同的设置，则纯误差自由度（表示为 DFPE）计算如下：
  
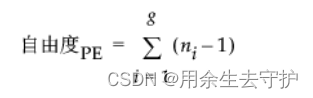
  其中，ni 是第 i 个组中的重复值数目。
• 失拟自由度是总误差自由度与纯误差自由度之间的差值。

平方和
记录每种误差来源关联的平方和 (SS)：

• 总误差平方和是相应的“方差分析”表的误差行中的平方和。
• 纯误差平方和是每个重复的观测组的平方和的总和。用纯误差平方和除以其自由度可估计给定的预测变量设置下的响应方差。该估计值不受模型影响。通常情况下，若有 g 个组，每组中每个效应具有相同的设置，则纯误差平方和（表示为 SSPE）计算如下：
  
  其中，平方和i 是每个观测响应与第 i 个组的响应均值之间差值的平方和。
• 失拟平方和是总误差平方和与纯误差平方和之间的差值。

均方
显示源的均方，它是平方和除以自由度的结果。与纯误差均方相比，较大的失拟均方表明模型拟合不佳。F 比提供正式检验。
F 比
显示失拟均方与纯误差均方之比。F 比检验的是以下假设：失拟估计的方差与纯误差均方相等，这可以解释为表示“无失拟”。
概率>F
列出失拟检验的 p 值。较小的 p 值指示失拟显著。
最大 R 方
列出仅基于这些效应的模型可实现的最大 R 方。纯误差平方和不随模型形式变化而变化。所以包含这些重复效应的模型可以解释的最大变异量等于：

该公式定义了最大 R 方。

5.弯曲

弯曲项: 加入中心点后回归模型引入的额外平方和(加入中心点前后的回归平方和之差)，可以简单看做是平方项的混杂，自由度为1，无法确定是代表哪个项或合并了哪些项。

在回归分析时：
SS=（Y1-Y2）^2/（1/M+1/N）：
1.Y1为Y在中心点所有值的平均值，Y2为Y所有其他因子组合的平均值。
2.M为：中心点的自由度，N为其他因子组合的自由度。
3.初步观察Y1-Y2的大小，如果比较小，表示弯曲的不严重。那个立方体图形里，所有因子的组合不是顶点就是轴点，和中心点的组成的曲面。这个差反映了这个曲面程度

《工程统计学》《Engineering statistics》.Douglas C.Montgomery

6.纯误差

即自变量取值相等时的重复误差。如果只有中心点重复，就是中心点重复误差。实质是模型外因子的波动。当某个主效应因子和所有包含它的项都被删除后(即排除到模型之外)，这些删除项对新模型来讲也是重复误差，全部并入纯误差项。

最初全模型时，纯误差就是剥离了弯曲项的残差，其自由度等于总样本量N减去回归方程系数个数k(因为k个回归系数必须由k个样本值联立方程求得，所以k个系数占用了k个自由度)。考虑要单列弯曲项，因此残差再扣除中心点拟合值一个自由度。

删减后模型中，残差项下的纯误差、不显著的失拟项、弯曲项实质一样，都是误差的估计，只是人为区分。

具体来说：
只有中心点重复时，初始纯误差自由度为中心点个数减1。(减1是因为要减去均值)

各点都有重复时，初始纯误差自由度等于各点重复数分别减1再相加。
有主效应及其全部衍生项被删减后，要并入纯误差项中。

失拟项和弯曲项如果不显著，被移出模型，放入残差项中，实质也是纯误差(噪声)，但常不列入纯误差项，而单列在残差项下。因为主效应或其它相关项未删除干净。
所以这时残差与纯误差只是人为区分。

(注意，扯远一点，在无重复误差的线性回归中，X值或拟合值十分接近的点称为近邻点，近邻点波动也视为纯误差。)
3)简单说，带中心点的二水平因子试验中的失拟项就是当主效应因子存在于模型中时，被删除的相关交互项。
这时弯曲项就是加入中心点后产生的混杂项。

含平方项的响应曲面试验中，增加了轴点数据，总自由度大大增加了，单个因子的自由度也增加了。弯曲效应已经分到各个二次项里，是可分析的，所以软件通常不列出弯曲项。

DOE(包含响应曲面)中很关键的一点是自由度守恒。从统计软件输出表中看模型删减前后自由度的变化就知道删减的项转到哪里去了。
回归分析中的失拟通常指残差波动扣除纯误差后的部分，相当于DOE中弯曲项+失拟项。纯误差一般通过重复误差或近邻点误差(非常靠近的x值看做是相同的x值)来估计。

7.自由度

弯曲项自由度: 加入中心点后回归模型引入的额外平方和(加入中心点前后的回归平方和之差)，可以简单看做是平方项的混杂，自由度为1
纯误差自由度：中心点重复时，初始纯误差自由度为中心点个数减1
失拟自由度：是总误差自由度与纯误差自由度之间的差值
误差自由度： 模型的自由度（s-1）以及误差自由度的自由度（n-s）

说明：
通常df=n-k。其中n为样本数量，k为被限制的条件数或变量个数，或计算某一统计量时用到其它独立统计量的个数。自由度通常用于抽样分布中。
根据模型的自由度（s-1）以及误差自由度的自由度（n-s），可以确定一个F分布。由该F分布的概率密度函数和F0，可以进一步计算出在该F分布中大于F0 的p值，p=pr（x>F0）

方差分析

“方差分析”报表提供用于将拟合模型与所有预测值都等于响应均值的模型进行比较的计算。
注意：若在“拟合模型”启动窗口中输入了“频数”或“权重”变量，“方差分析”报表中的条目将进行调整以符合频数和权重中的说明。
“方差分析”报表包含以下列：
源
列出变异的三个来源：模型、误差和校正总和。
自由度
提供每个变异来源关联的自由度 (DF)。

• 校正总和自由度始终为观测数减 1。
• 校正总和自由度分为模型自由度和误差自由度：
  模型自由度是用于拟合模型的参数数目（截距除外）。

误差自由度是校正总和自由度与模型自由度之间的差值。
平方和
提供每个变异来源关联的平方和 (SS)。

• 总（校正总和）平方和是响应值与样本均值之间的差值平方和。它表示响应值中的总变异。
• 误差平方和是拟合值与实际值之间的差值平方和。它表示拟合模型尚未解释的变异。
• 模型平方和是校正总和平方和与误差平方和之间的差值。它表示模型解释的变异。

均方
列出均方。每个均方都是平方和除以其相应自由度的结果。
注意：误差均方的平方根与“拟合汇总”报表中的 RMSE 相同。
F 比
显示模型均方除以误差均方的结果。F 比是以下检验的检验统计量：检验模型是否与所有预测值都是响应均值的模型显著不同。
概率>F
提供检验的 p 值。“概率>F”值测量在除截距之外的所有参数均为零的情况下，获取与观测到的 F 比同样大的 F 比的概率。较小的“概率>F”值指示观测到的 F 比不太可能。这样的值被视为模型中至少有一个显著效应的证据。

8.模型的理解

第一节：R-Sq的理解
R-Sq一拟合的总效果多元全相关系数，是指总变动中用回归可说明的变动占有比率。此值越接1越好。

R-Sq有一个缺点，当增加一个新的自变量进入模型后，不管新增加的自变量效应是否显著，R-Sq都会增加一些，因而在评价是否该增加此自变量进入回归方程时，使用R-Sq就没有价值了，为此引入了R-Sq（adj）

另外：
学习：《应用回归分析》-人大版.何晓群-自变量与逐步回归
R2=1-SSerror/SStotal R2（adj）=1-（SSerror/（n-p））（SStotal/（n-1），n为总项数，p为回归式中的项数。
两个值越接近越好。两个值越大越好，越大说明你的回归式越好。

当给模型增加自变量时，复决定系数也随之逐步增大，然而复决定系数的增大代价是自由度的减少，因为残差自由度等于样本个数与自变量个数之差。自由度小意味着估计和预测的可靠性低。这表明一个回归方程涉及的自变量很多时，回归模型的拟合在外表上是良好的，而区间预报和区间估计的幅度则变大，以至失去实际意义。这里回归模型的拟合良好掺进了一些虚假的成分。为了克服样本决定系数的这一缺点，我们设法把R2给予适当的修正，使得只有加入“有意义”的变量时，经过修正的样本决定系数才会增加，这才是所谓的自由度调整复决定系数。R（a）2=1-（n-1）（1-R2）/（n-p-1）
可以看出，尽管1-R2随着自变量的增加而减少，但由于其前面的系数（n-1）/（n-p-1）起折扣作用，才使R（a）2随着自变量的增加不一定增大。当所增加的自变量对回归的贡献很小时，R（a）2反而可能减少。

第二节：R-Sq（adj）的理解
R-Sq（adj）一修正的多元全相关系数。

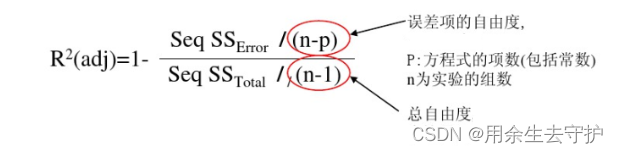
R-Sq（adj）是扣除了回归方程中包含项数的影响的相关系数，因而可以准确的反映模型的好坏。它同样越接近1越好。在实际应用中，回归方程中的项数P总会大于等于1，因而可以看出，R-Sq（adj）总比R-Sq稍小一点，因而判断模型的优劣可以从二者的接近程度，二者之差越小则说明模型越好

第三节：S的理解

在回归分析中，观测值与理论模型之间可以有误差，但我们总是假定，这个误差是服从以0为均值，以o2为方差的正态分布。在ANOVA表中，残差误差（Residual error）
那一行中的平均离差平方和（adjMS）的数值则正好是o2的无偏估计量，我们将其叫做均方误（MSE），所以我们可以认为s是o的估计。因此s在模型好坏分析中起着关键的作用，s值越小表明模型越好。

9.其它问题

1. 回归分析的相关系数大于95%是不是就可以用于生产？
   一般是要求看R-square（aji）是否大于80%，回归拟合就比较好了.
   分析后一般要进行模型优化，比如异常点剔除，leverage作用，最佳子集回归等等.
   还要模型检验，比如残差分析，实际试做.
2. 方差分析之前是不是必须先进行等方差检验，如果标准方差相差较大，是不是就不能使用方差分析
   等方差检验如果显示方差差别显著，就会影响我们认识和判断因素对输出平均值的作用.
   但并不意味着ANOVA就不可用，有时候，所研究的因素里有一个对输出的结果稳定性很显著的话，就会出现上述情况，那也是有价值的.
3. 主效应分析显示某个变量确实后导致输出结果之间变化较大，可以判定为影响因素，即是回归方程的相关系数却非常小，是不是也可以确定为主因素.
   当然，ANOVA中的回归方程R2是告诉你线性回归方程的可解释的比例。
   而ANOVA的分析是基于组内变异来显示某个因素对结果的影响的.如果碰到交互作用或二次项比较显著的话，就会在ANOVA中出现你所说的情形。

三、DOE

1.中心点

用中心点有两点理由：

1. 第一，获得一个曲率的估计，
2. 第二就是提供一个误差项估计以及误差项的自由度.中心点越多，对这两者的估计越准.
   指导原则是，中心点试验个数至少应与实验中因子的个数一样多。

2.模型的简化

• 去除不重要的交互作用
• 也要从模型中去除中心点

备注： 分析全模型的时候，要选上中心点

四、回归与相关

6sq.net

1.直线回归分析

直线回归是用直线回归方程表示两个数量变量间依存关系的统计分析方法，属双变量分析的范畴。
1.直线回归方程的求法
（1）回归方程的概念：
直线回归方程的一般形式是Y（音yhat）-a+bx，其中x为自变量，一般为资料中能精确测定和控制的量，Y为应变量，指在规定范围内随机变化的量。a为截距，是回归直线与纵轴的交点，b为斜率，意为x每改变一个单位时，Y的变化量。
（2）直线回归方程的求法
确定直线回归方程利用的是最小二乘法原理，基本步骤为：
1）先求b，基本公式为b=11kx-SSx/SSx其中，为x，Y的离均差积和。1w为x的离均差平方和；
2）再求a，根据回归方程a等于Y的均值减去均值与b乘积的差值。
（3）回归方程的图示：
根据回归方程，在坐标轴上任意取相距较远的两点，连接上述两点就可得到回归方程的图示。应注意的是，连出的回归直线不应超过x的实测值范围。
2.回归关系的检验
回归关系的检验又称回归方程的检验，其目的是检验求得的回归方程在总体中是否成立，即是否样本代表的总体也有直线回归关系。方法有以下两种：
（1）方差分析
其基本思想是将总变异分解为SS归和SS会，然后利用下检验来判断回归方程是否成立。
（2）t检验
其基本思想是利用样本回归系数b与总体均数回归系数B进行比较来判断回归方程是否成立，实际应用中因为回归系数b的检验过程较为复杂而相关系数r的检验过程简单并与之等价，故一般用相关系数的检验来代替回归系数b的检验。
3.直线回归方程的应用
（1）描述两变量之间的依存关系；利用直线回归方程即可定量描述两个变量间依存的数量关系
（2）利用回归方程进行预测；把预报因子（即自变量x）代入回归方程对预报量（即因变量Y）进行估计，即可得到个体Y值的容许区间。
（3）利用回归方程进行统计控制
规定Y值的变化，通过控制x的范围来实现统计控制的目标。如已经得到了空气中NO，的浓度和汽车流量间的回归方程，即可通过控制汽车流量来控制空气中NO2的浓
4.应用直线回归的注意事项
（1）做回归分析要有实际意义；
（2）回归分析前，最好先作出散点图；
（3）回归直线不要外延。

2.直线相关分析

1.直线相关的概念
直线相关分析是描述两变量间是否有直线关系以及直线关系的方向和密切程度的分析方法。用以描述两变量间相关关系的指标是相关系数（常用表示），两变量间相关关系的种类有正相关（0r<1）、负相关（-1<r<0）、零相关（r=0）、完全相关（r]=1）等。相关分析对资料的要求是两变量（xy）均是符合正态分布的随机变量。
2.相关系数的计算
相关系数是xY的离均差积和、除以X的离均差平方和。与Y的离均差平方和之积的算术平方根的商。故此相关系数又被称为积差相关系数。
3.相关系数的假设检验
相关系数检验的目的是判断两变量的总体是否有相关关系，方法有（检验和查表法，检验法是样本与总体的比较，查表法是直接查相关系数界值表得到相应的概率p。

3.直线相关与回归的区别与联系

区别：
1.相关说明相关关系，回归说明依存关系；
2.r与b有区别：
3.资料要求不同。
联系：
1.r与b值可相互换算；
2.r正负号一致；
3.r与b的假设检验等价；
4.回归可解释相关。相关系数的平方2（又称决定系数）是回归平方和与总的离均差平方和之比，故回归平方和是引入相关变量后总平方和减少的部分。

4.等级相关分析

等级相关分析适用于资料不是正态双变量或总体分布未知，数据一端或两端有不确定值的资料或等级资料。常用的Spearman等级相关系数r，是利用x，Y的秩次来进行直线相关分析的。因此当x，Y的相同秩次较多时，计算出的r。需矫正。同样的，等级相关系数，也需要进行假设检验。
五、相关分析应用中的注意事项
1.相关分析要有实际意义；
2.相关关系不一定都是因果关系；
3.相关系数：假设检验中p的大小不能说明相关的密切程度；
4.直线相关和等级相关有各自不同的适用条件。

---

总结

分享：
我们应该舍弃那种规定的、划一的、被动的强记事实方法，而将这种积极的、滋长的个人快乐定为理想目标。文凭和学分如一旦废除，或仅仅值其所实值，学问的寻求即能趋于积极。因为那时做学生的至少要自问为什么而读书。