无需依赖专家标注，自动识别病理切片的鉴别性形态特征，揭示组织由良性演变为恶性的轨迹

小罗碎碎念

这篇发表于《Nature Communications》的文章提出了一种名为组织形态表型学习（HPL）的自监督学习方法，专门用于从无注释的病理切片中挖掘组织形态学癌症表型。

该方法无需依赖专家标注，通过自动发现病理切片中的鉴别性特征，将切片聚合成形态相似的簇，形成组织形态表型图谱（HP-Atlas），能够揭示从良性到恶性组织的演变轨迹，并关联组织学、分子和临床表型。

HPL的核心流程包括WSI预处理（切片提取与染色标准化）、基于Barlow Twins的自监督学习获取切片特征向量、利用Leiden社区检测构建组织形态表型簇（HPCs），以及将WSI或患者表示为HPCs的组成向量，为后续的临床和分子关联分析奠定基础。

在肺腺癌研究中，HPL识别出46个具有生物学意义的HPCs，这些簇不仅与已知的肿瘤生长模式、淋巴细胞浸润程度等组织学特征高度吻合，还能有效预测患者的总体生存和无复发生存，在外部队列中展现出稳健的性能（如NYU队列总体生存预测的c-index达0.65，无复发生存预测达0.74）。

进一步分析表明，HPCs可与转录组学免疫特征（如TIL密度、增殖信号）、细胞类型分布及病理学家标注的组织学亚型显著关联，例如与良好预后相关的HPCs常富集淋巴细胞浸润和炎症相关分子特征，而与不良预后相关的HPCs则多表现为实体型生长模式和低免疫浸润。

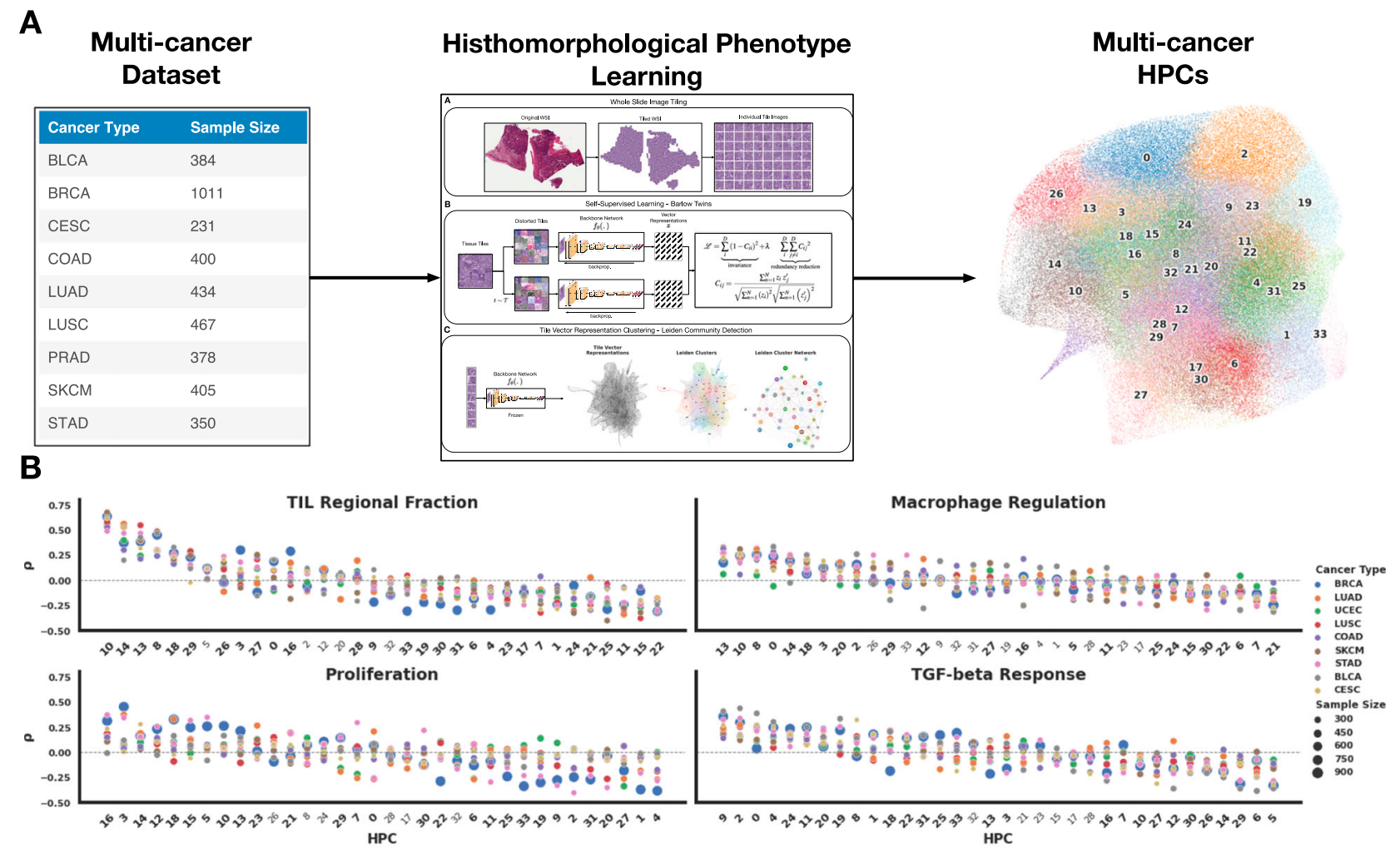
在多癌症研究中，HPL同样表现出色，不仅能以高准确率（AUC达0.99）区分肺腺癌（LUAD）和肺鳞状细胞癌（LUSC），还在10种癌症类型中识别出具有跨癌种普遍性的组织形态模式。

这些模式与免疫特征（如T细胞浸润、TGF-β应答）和患者生存密切相关，例如富含淋巴细胞浸润的HPCs多与良好预后相关，而实体型生长和基质纤维化相关的HPCs则常提示不良结局。

该方法为医学AI研究提供了一种无需标注即可挖掘病理图像深层生物学意义的新范式，尤其在辅助癌症诊断、预后预测和生物标志物发现方面具有重要应用价值。

---

交流群

欢迎大家加入【医学AI】交流群，本群设立的初衷是提供交流平台，方便大家后续课题合作。

目前小罗全平台关注量71,000+，交流群总成员1600+，大部分来自国内外顶尖院校/医院，期待您的加入！！

由于近期入群推销人员较多，已开启入群验证，扫码添加我的联系方式，备注姓名-单位-科室/专业，即可邀您入群。

---

医学AI资料获取

作者是一支以国内外硕博为主的学生团体，覆盖医学AI主流研究领域；团队现有50余人，持续欢迎新的小伙伴加入！

团队官网上传了大量优质的学习资料，包括但不限于每次免费公开课的回放，顶刊复现教程等等！

感兴趣的可以扫码或者点击链接访问作者团队的官网：https://www.lxltx.site/

---

一、文献概述

本文提出了一种名为组织形态表型学习（HPL）的自监督方法，用于从无注释的病理切片中自动发现组织形态学表型，无需专家标注，可应用于癌症诊断、预后预测等领域，且在多癌症研究中表现稳定。

---

1-1：研究背景与问题

• 癌症诊断和治疗决策依赖病理学家从显微镜图像中提取复杂信息，但该过程耗时且易受人为偏差影响。
• 有监督深度学习方法虽强大，但受限于训练所用标注的成本和质量，且可能限制新生物标志物的发现，还存在“黑箱”问题，影响信任和治疗决策。
• 半监督和弱监督方法虽能缓解标注瓶颈，但在提供组织切片的广泛临床和生物学意义方面存在不足。
• 无监督和自监督方法无需标签，仅从图像信息中创建组织图像表示，在组织病理学领域的应用逐渐受到关注。

---

1-2：HPL方法

• 核心原理：通过自监督学习和社区检测，从大量 whole - slide images（WSI）中发现组织形态表型（HP），即不同的形态组织模式，无需专家提供标签或注释。
• 主要步骤
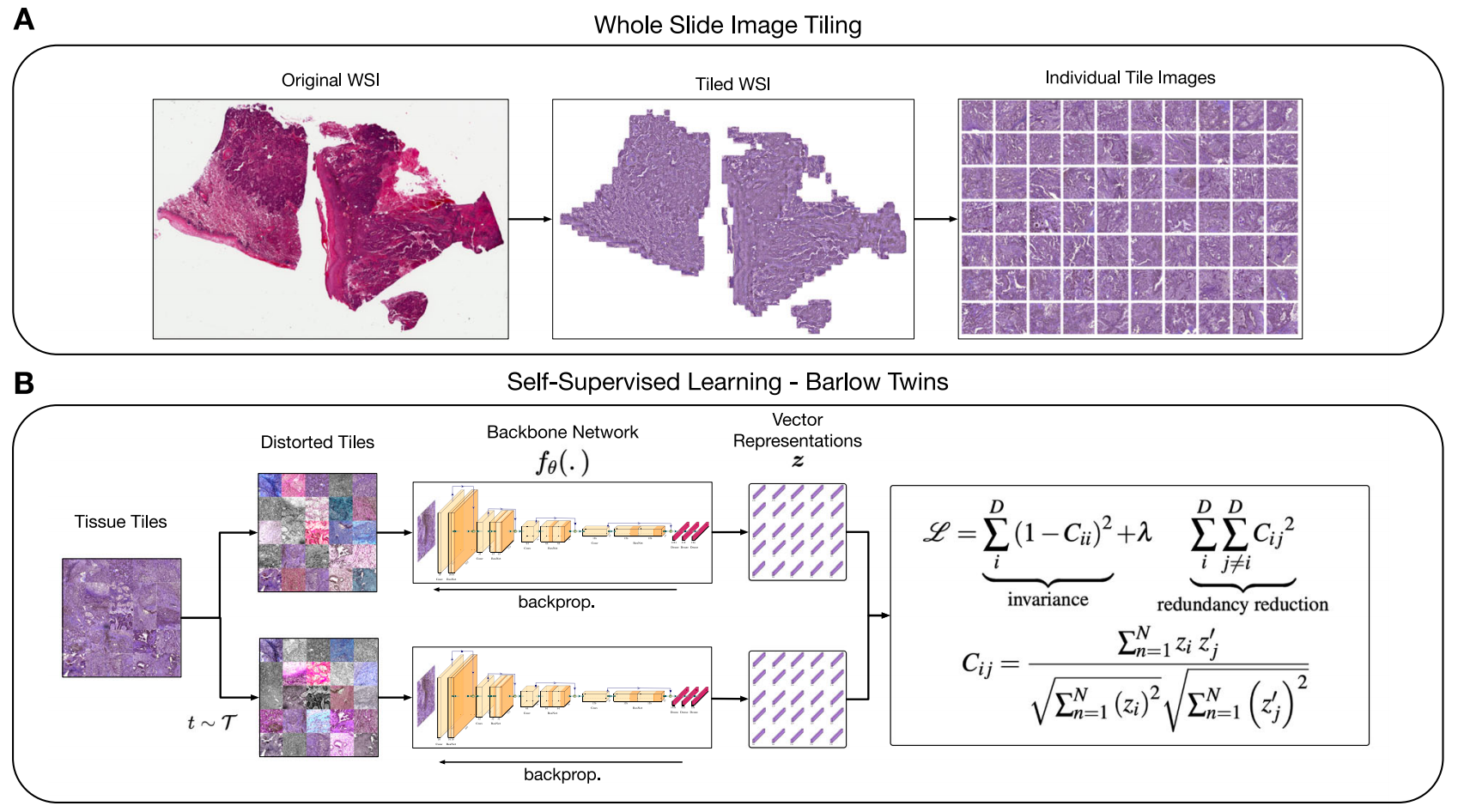
  • WSI预处理：将WSI分割为224×224无重叠的切片，过滤掉组织面积不足60%的切片，并进行染色标准化。
  • 组织切片的自监督学习：使用Barlow Twins在训练集切片上进行自监督学习，捕捉组织中不同的形态模式，并将其表示为向量，且确保表示对颜色和轻微缩放失真具有不变性。
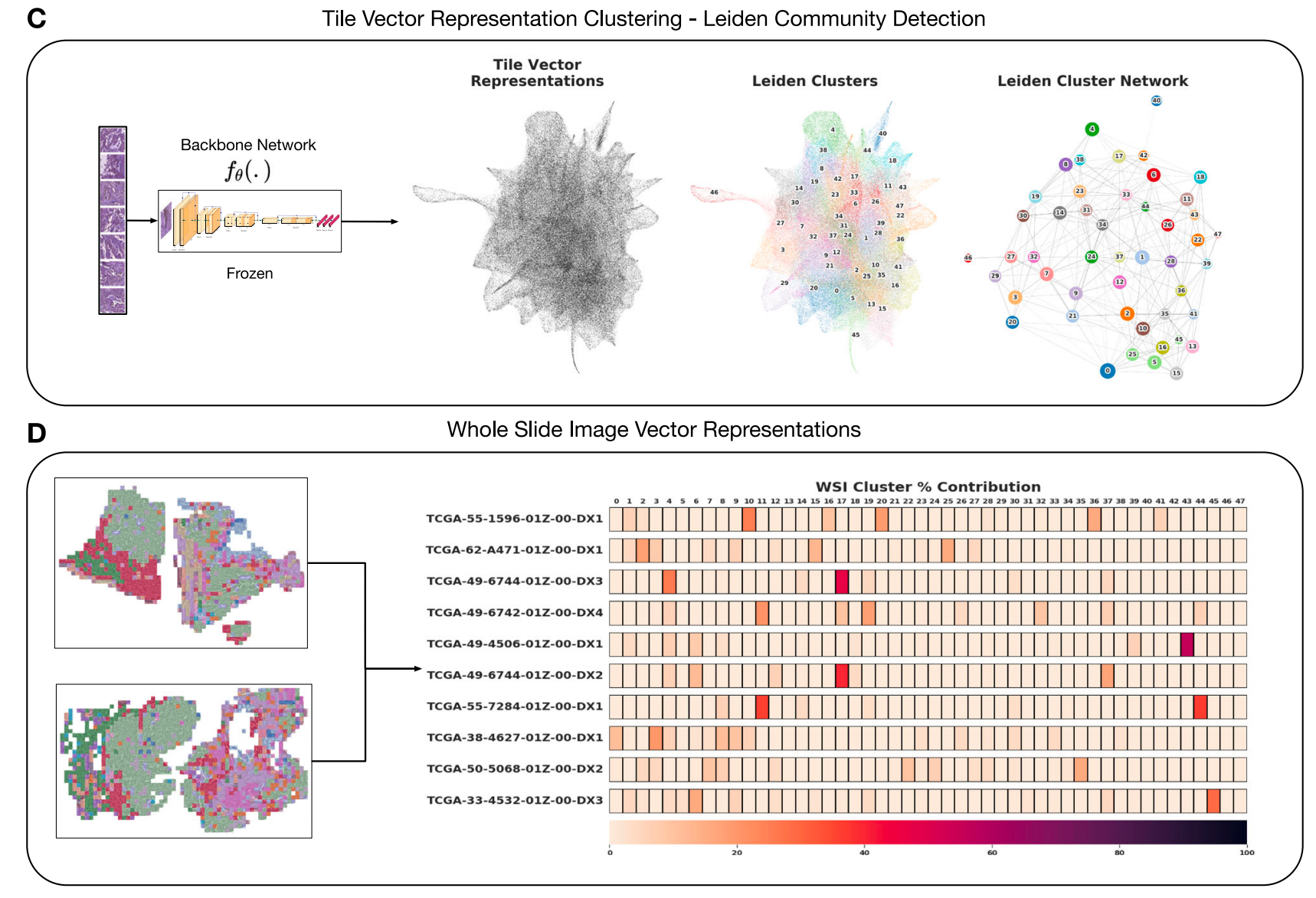
  • 组织切片表示聚类为组织形态表型簇（HPCs）：基于切片向量表示定义最近邻图，然后使用Leiden社区检测找到HPCs，并通过一种自监督方法选择HPCs的数量，该方法权衡了HPC的紧凑性和在不同机构队列中的泛化能力。
  • HPC表征：每个WSI或患者可通过HPC的频率来描述，将其转换为组成向量，该向量的维度等于HPC的总数，每个维度表示每个HPC覆盖的面积占总组织面积的百分比。

---

1-3：实验与结果

• 肺腺癌组织形态表型的从头映射
  • 将HPL应用于TCGA的肺腺癌WSI，经过处理得到约411,000个切片表示向量，使用UMAP进行降维后，通过Leiden社区检测确定了46个HPCs。
  • 测试表明，这些簇不是患者特异性或机构特异性的，具有高度的复现性。
  • 专家病理学家对每个簇的100个随机切片进行注释，结果显示这些簇对应有意义的组织形态表型，在UMAP上按组织成分有明显分离，且能捕捉到从良性到恶性组织的轨迹等。
• HPL识别与临床结果相关的肺腺癌预后组织形态表型
  • 定义患者向量表示，使用Cox比例风险模型测试HPCs在预测总体生存和无复发生存方面的相关性。
  • 在肺腺癌总体生存分析中，在TCGA测试集上的平均一致性指数（c - index）为0.60，在NYU独立集上为0.65；在无复发生存研究中，在NYU队列上的平均c - index为0.74，且结果具有稳健性。
• HPL发现的模式与细胞类型、组织学生长模式和分子表型的系统关联
  • 通过Spearman等级相关、双样本Kolmogorov - Smirnov检验和超几何检验等方法，将HPCs与转录组学免疫特征、细胞类型和组织学亚型注释等关联起来。
  • 结果显示，与较好预后相关的HPCs在组织学上富含淋巴细胞浸润，与多种反映炎症细胞的分子特征呈正相关；与较差预后相关的HPCs淋巴细胞浸润轻微或稀疏，与增殖等分子特征呈正相关等。
• HPL在多癌症中的应用
  • 区分肺腺癌（LUAD）和肺鳞状细胞癌（LUSC）：使用TCGA作为训练集，NYU作为独立测试集，通过逻辑回归在WSI向量表示上进行分类，TCGA测试集的平均AUC为0.930，NYU独立测试集为0.990，且具有稳健性。
  • 多癌症数据集分析：对TCGA中10种癌症类型的数据集应用HPL，发现了与特定分子特征相关的组织形态模式，这些模式可用于区分癌症亚型或识别预测总体生存的通用癌症表型，且一些形态学原理在不同癌症中具有普遍性。

---

1-4：讨论与结论

• HPL是一种自监督方法，能从WSI中从头识别组织形态表型，无需昂贵的注释，并在决策过程中提供清晰的见解。
• 在肺腺癌中的应用表明HPL的HPCs重现了已建立的LUAD生长模式，且在生存预测等方面表现良好。
• 在多癌症分析中，HPL能辅助识别和解释跨癌症类型的HPCs，表现出良好的性能和稳健性。
• 总体而言，HPL有潜力应用于任何癌症类型，为研究跨癌症类型的组织形态表型提供了强大的发现方法，具有预后和生物标志物潜力。

---

二、方法

2-1：数据集

肺肿瘤类型预测任务

对于肺肿瘤类型预测任务，作者使用了癌症基因组图谱（TCGA）以及纽约大学（NYU）的一个独立外部队列，本研究中标记为 $NY{U}_2$ ，包括福尔马林固定石蜡包埋（FFPE）和苏木精-伊红（H&E）染色的全切片图像（WSIs）。

TCGA队列由1021张全切片图像组成，其中513张为腺癌（LUAD），508张为鳞状细胞癌（LUSC）。 $NY{U}_2$ 由138张全切片图像组成，其中72张为LUAD，66张为LUSC，与库德雷等人使用的队列相当。 ${}^8$

必要时，病理学家的诊断会通过免疫组织化学染色（分别用于LUAD和LUSC的TTF-1和p40）进行补充，从而得到一个标签可靠的干净数据集。

---

腺癌总生存分析

腺癌总生存分析使用了TCGA的LUAD队列以及本研究中标记为 ${\mathrm{NYU}}^1$ 、在本研究中标记为 $NY{U}_1$ 的另一个队列。

TCGA队列由442名患者组成，删失率为0.64，涵盖所有阶段（1 - 4期）， $NY{U}_1$ 由276名患者组成，删失率为0.80，仅包括1期病例。

关于这两个队列的更多详细信息，如Kaplan - Meier曲线以及随访时间之间的分布比较，可在补充图28中找到。

---

腺癌无复发生存分析

腺癌无复发生存分析聚焦于来自 $NY{U}_1$ 的全身和局部区域复发类型。

它由三种类型组成：全身、局部区域和新发原发性。由于作者关注的是全身和局部区域复发，因此对新发原发性病例进行了删失。

仅使用纽约大学队列的背后动机是基于更详细的复发信息和更长的随访时间。该数据集由与总生存分析中使用的来自 $NY{U}_1$ 的相同276名患者组成，复发的删失率为0.82。

此外，70张纽约大学全切片图像有病理学家对组织学亚型（实性、乳头状、微乳头状、腺泡状和鳞屑状）的非详尽手动注释，允许对单个切片进行标记。关于无复发生存队列的更多详细信息，可在补充图28中找到。

---

作者的多癌分析使用了癌症基因组图谱（TCGA）中的10种癌症类型。

完整队列由279例膀胱尿路上皮癌（BLCA）患者、364例乳腺浸润性癌（BRCA）患者、187例宫颈鳞状细胞癌和宫颈内膜腺癌（CESC）患者、369例结肠腺癌（COAD）患者、366例肺腺癌（LUAD）患者、367例肺鳞状细胞癌（LUSC）患者、247例前列腺腺癌（PRAD）患者、363例皮肤黑色素瘤（SKCM）患者、278例胃腺癌（STAD）患者和395例子宫内膜癌（UCEC）患者组成。

癌症类型和患者数量是可用的TCGA癌症类型与免疫特征信息 ${}^{54}$ 的交集；

作者还选择了至少有150个注释样本的癌症类型。

结果部分使用的免疫图谱特征来自索尔松等人发表的对33种癌症类型的免疫特征分析。 ${}^{54}$ 这些免疫特征来自TCGA的批量RNA测序数据。

---

2-2：全切片图像预处理

作者使用公开可用的DeepPATH管道 ${}^8$ 将每个全切片图像（WSI）划分为大小为 $224\times 224$ 、放大倍数为 $5\mathrm{X}$ 的非重叠图块（图块重新采样以确保每像素 $2.016\mu \mathrm{m}$ ）以及放大倍数为 $20\mathrm{X}$ 的图块（图块重新采样以确保每像素 $0.504\mu \mathrm{m}$ ），过滤掉总面积中组织占比小于 $60\%$ 的图像（将平均灰度值高于230的背景像素视为组织像素），并使用Reinhard方法 ${}^{42}$ 进行染色归一化，该方法旨在使图像的均值和标准差与目标值匹配。

这里不是将图像归一化到给定的图像参考，而是将来自TCGA数据集的100个随机图块的平均值作为目标值。

---

2-3：自监督学习

自监督学习旨在基于数据的特征创建有用的数据表示，与监督方法不同的是，它无需依赖昂贵的人工标注来实现这一点。这些方法使用一个前置任务作为手段，将相关特征信息捕捉到每个实例表示中。随后，这些表示可用于下游任务。

自监督学习中的一种常见设置是使用数据增强管道 $T$ 以创建对图像失真 ${}^{78}$ 具有不变性的表示，以及使用骨干网络 $f_{\theta }$ 将图像投影到潜在空间 $z$ ，不同的方法在这个潜在空间中定义前置任务目标。

Barlow Twins ${}^{44}$ 旨在创建对失真具有不变性的表示，同时最小化表示中特征维度之间的冗余信息。它使用两种不同的变换对批次中的每个图像进行失真处理 $\left\{{\tilde{x}}_i=t\left(x_i\right),{\tilde{x}}_i^{\prime }=t^{\prime }\left(x_i\right);t\sim T,t^{\prime }\sim T\text{and}{\left[x_n\right]}_{n=1}^N\right\}$ ，并使图像通过骨干网络 $f_{\theta }$ 以获得潜在表示 $z\in R^D/D=128;z_i=f_{\theta }\left({\tilde{x}}_i\right),z_i^{\prime }=f_{\theta }\left({\tilde{x}}_i^{\prime }\right)$ 。

紧接着，对每个变换集的表示进行批归一化 Z∈RNxD;{Z,Z′}Z \in {R}^{NxD};\left\{ {Z,{Z}^{\prime }}\right\}Z∈RNxD;{Z,Z′} ，并计算 $C\in {\left[-1,1\right]}^{DxD}$ 作为沿着批次维度在 {Z,Z′}\left\{ {Z,{Z}^{\prime }}\right\}{Z,Z′} 之间计算的互相关矩阵。

损失由两项定义，不变性项试图创建对失真具有不变性的表示，冗余减少项则将相关矩阵的非对角特征最小化，以防止它们之间存在任何冗余信息（公式(2)）。

参数 $\lambda$ 用作加权因子，以平衡对角项和非对角项数量上的差异：
$$\mathcal{L}=\overline{\sum _i^D{\left(1-C_{ii}\right)}_{\text{invariance }}^2+\lambda \underbrace{\sum _i^D\sum _{j\ne i}^D{C}_{ij}^2{c}_{ij}^2\text{ calundancy reduction }};C_{ij}=\frac{\sum _{n=1}^N{\mathbf{z}}_i{\mathbf{z}}_j^{\prime }}{\sqrt{\sum _{n=1}^N{\left({\mathbf{z}}_i\right)}^2}\sqrt{\sum _{n=1}^N{\left({\mathbf{z}}_j^{\prime }\right)}^2}}}$$

有必要提及Barlow Twins如何避免前置任务的平凡解，即在自监督学习中也称为塌缩的情况，即不同图像的表示保持恒定值。

该方法通过减少冗余来避免塌缩，强制潜在表示的特征之间去相关，并在计算互相关矩阵之前对批次向量表示进行批归一化。已经证明它不像对比方法 ${}^{45,79}$ 那样依赖于批次大小。

---

骨干网络 $f_{\theta }$ 是一个卷积神经网络（CNN），用作组织图像的特征提取器。

在作者的工作中，作者使用了一个由几个ResNet层 ${}^{80}$ 和一个自注意力层 ${}^{81,82}$ 组成的CNN。这种架构与Quiros等人 ${}^{36}$ 使用的架构相似，在他们的工作中已证明该架构是一种有效的特征提取器。

更具体地说，骨干卷积神经网络（CNN）由19层（传统卷积层和残差网络层）组成，并在特征图 $56\times 56\times 32$ 处添加了一个自注意力层。

与传统的 $3\times 3$（例如ResNet-50）相比，卷积核大小范围从 $7\times 7,5\times 5$ 到 $4\times 4$；作者引入这些变化以捕获更大的交互感受野。

整个网络的可训练参数数量为21,197,785。此外，作者使用谱归一化，这是一种已被证明能有效限制梯度更新大小并稳定训练的归一化技术 ${}^{83}$。

作者在补充图29中对CNN层进行了详细描述。

---

作者使用 $250\mathrm{K}$ 切片图像对自监督模型进行了60个轮次的训练，批次大小为64。

作者使用了单个GPU（NVIDIA Titan Xp 12GB/NVIDIA RTX 24GB），训练时间在48到72小时之间。

作者的方法允许在合理的时间内训练自监督模型，而无需大型GPU集群。一旦骨干网络 $f_{\theta }$ 训练完成，就将其冻结，仅用于将组织切片投影到特征表示中。

---

为确保在切片子集上的训练不会影响性能，作者还使用训练集的完整切片运行了训练和高倍镜下病理图像学习（HPL）流程，采用5折交叉验证方法以及与之前发表文章中类似的训练/验证划分 ${}^{30,38}$，详细的划分可在作者的github页面https://github.com/AdalbertoCq/Histomorphological-Phenotype-Learning/tree/master/utilities/files/LUAD上下载。

此外，作者将高倍镜下病理图像学习（HPL）性能中用巴洛双胞胎（Barlow Twins）替换为另一种相关的自监督学习方法——深度信息噪声对比学习（DINO）进行了比较。

补充图13展示了这两种方法在肺腺癌（LUAD）生存性能上的比较。总体而言，两种自监督方法的性能相当。然而，深度信息噪声对比学习（DINO）的一致性指数相对于 Leiden 分辨率参数波动更大（导致聚类更多/更少），而巴洛双胞胎（Barlow Twins）在不同分辨率下保持相当稳定。

---

2-4：聚类表示

Leiden社区检测算法 ${}^{48}$ 已被证明是一种在图结构中发现紧密连接社区的成功算法。

它是作为Louvain算法 ${}^{84}$ 的改进版本推导而来，使用启发式方法在图中找到划分。

该算法首先将图中的每个节点分配到一个不同的社区，然后迭代执行以下步骤，直到网络不再有进一步变化。

首先，对于每个节点，算法会评估当节点从当前社区移动到相邻社区时的模块度增益；如果有正增益，则将节点保留在新社区中。在初始遍历之后，对改变社区的节点重复此过程，直到达到局部最大值，从而找到图的一个划分。其次，通过可能进一步拆分一些先前定义的社区来细化先前的划分。

这是通过如果随机合并一个节点到一个社区会增加模块度来实现的，这允许进一步探索划分空间并避免连接不良的社区，这是Louvain算法 ${}^{48}$ 的一个缺点。

最后，聚合每个社区中的节点，并将社区视为下一次迭代中的节点。

模块度由公式（3）定义，其中 $e_c$ 是社区中的边数， $\mathrm{c},\frac{K_c^2}{2m}$ 是预期的边数，其中 $K_c$ 是社区中节点度数的总和， $c$，并且 $m$ 是网络中的总边数。 $\gamma$ 是分辨率参数，较高的值会导致更多社区，较低的值会导致更少社区：

$$\mathcal{H}=\frac{1}{2m}\sum _c\left(e_c-\gamma \frac{K_c^2}{2m}\right)\text{\hspace{1em}(3)}$$

---

为了从自监督组织表示中找到组织形态学表型簇（HPCs），作者通过对训练集中随机采样的200,000多个切片使用$K$最近邻$\left(K=250\right)$创建了一个图，并使用 Leiden 社区检测来定义簇。

【注意：对于训练数据集的异质性和不平衡导致交叉验证和外部队列表现不佳的研究，可能需要考虑使用更多切片，并使用该领域常用的技术（如对少数数据集进行过采样或对其中一个数据集进行数据增强）来平衡训练数据集】

随后，作者通过再次使用训练集向量与附加集的每个向量之间的$K$最近邻，将簇分配给附加集的向量表示。

---

作者首次执行聚类过程，以识别和去除背景和伪影切片的表示。

一旦去除这些表示，作者再次运行聚类过程，以便这些无信息的切片表示不会干扰从 Leiden 算法中找到的组织群落数量。

最后，作者提出以下方法来设置$\gamma$，从而选择 HPC 的数量。

---

为了平衡 HPC 聚集在一起的紧密程度及其跨不同机构队列的泛化能力，作者在 HPC 紧凑度$(C_{{\gamma }_i}$ - 公式（4））和每个 HPC 中机构的平均出现率$(AI{P}_{{\gamma }_i}$ - 公式（5））之间进行权衡。

这种 Leiden 分辨率选择方法特定于作者在此处要解决的问题，使用 TCGA 多机构数据集作为训练集，并且作者希望识别受其来源机构影响尽可能小的特征。

不同的目标可能需要选择不同的阈值选择策略。

---

对于每个${\gamma }_i$分辨率值（HPC 集），作者将紧凑度$C_{{\gamma }_i}$测量为 HPC $n$ 的质心 ${\mu }_n$ 与属于该 HPC $n$ 的每个切片向量表示 $z_i$ 之间的平均欧几里得距离 $d\left(.,.\right)$。这在公式（4）中显示，其中 $K$ 描述切片向量表示的总数，$M$ 是属于一个 HPC 的切片向量表示的数量。

$$C_{{\gamma }_i}=\frac{1}{K}\sum _{k=1}^{K}d\left(z_k,{\mu }_j\right)\text{ where }{\mu }_n=\frac{1}{M}\sum _{p=1}^M{z}_p\text{\hspace{1em}(4)}$$

同样，对于每个${\gamma }_i$分辨率值，作者将每个$\mathrm{HPC}AI{P}_{{\gamma }_i}$中机构的平均出现率测量为 HPC 的相对大小与 HPC 中存在的机构百分比的加权和。

作者使用 HPC 的相对大小作为加权因子，以便根据其对整个分区的影响相应地惩罚 HPC 偏差：偏差较大的较大 HPC 对任何下游任务的影响将大于较小的 HPC。

在公式（5）中，作者将 $N$ 定义为给定 ${\gamma }_i,t_n$ 的 HPC 数量，将 $n$ 定义为 HPC 中存在的机构数量，将 $T$ 定义为 TCGA 机构的总数。

作者还将 $s_n$ 定义为 HPC $n$ 的相对大小，计算为属于该 HPC 的切片表示数量除以切片总数 $K$。
$$AI{P}_{{\gamma }_i}=\frac{1}{N}\sum _{n=1}^N\left[s_n\ast \frac{t_n}{T}\right];AI{P}_{{\gamma }_i}\in \left(0,1\right)\text{\hspace{1em}(5)}$$

此外，为了实现前面提到的权衡，作者反转紧凑度 $C_{{\gamma }_i}$ 并通过平均机构出现率 $AI{P}_{{\gamma }_i}$ 对其进行加权。

在这种设置下，一组更紧凑的 HPC 将获得更接近最大值 $\max \left(C_{\gamma }\right)$ 的值，并且它们将因其跨机构泛化的能力而受到惩罚 $AI{P}_{{\gamma }_i}$（公式（6））：
$${\text{Score}}_{{\gamma }_i}=\left[\max \left(C_{\gamma }\right)-C_{{\gamma }_i}\right]\ast AI{P}_{{\gamma }_i}\text{\hspace{1em}(6)}$$

最后，作者根据得分函数显示出较大趋势变化并开始饱和的位置（肘部方法或曲线的拐点）选择最佳的 Leiden 分辨率。

在补充图1中，作者展示了本文中提出的三项研究中的每一项的最终得分图，用于识别最佳的 Leiden 分辨率，以及导致该曲线的中间图。

---

2-5：全切片图像和患者向量表示

作者将全切片图像和患者（一个或多个全切片图像）的表示定义为一个向量，其维度等于莱顿聚类$C$（即组织形态学表型聚类（HPC））的数量，其中每个维度描述了一个HPC对总组织面积的贡献百分比（公式（7））：

w={w0,w1,…,wC−1} where {wi∈[0,1]/∑i=0C−1wi=1}(7) w = \left\{ {{w}_{0},{w}_{1},\ldots ,{w}_{C - 1}}\right\} \text{ where }\left\{ {{w}_{i} \in \left\lbrack {0,1}\right\rbrack /\mathop{\sum }\limits_{{i = 0}}^{{C - 1}}{w}_{i} = 1}\right\} \tag{7} w={w0​,w1​,…,wC−1​} where {wi​∈[0,1]/i=0∑C−1​wi​=1}(7)

为了在线性模型中使用这些全切片图像向量表示，作者进行中心对数比变换（公式（8））。逻辑回归或Cox比例风险等模型要求协变量之间相互独立。

全切片图像向量表示的原始定义是组合数据的一个例子，它违反了这个假设$\left(\sum _{i=0}^{C-1}{w}_i=1\right)$，中心对数比变换打破了变量之间的共依赖性，便于使用这些模型${}^{85}$。

此外，在应用中心对数比变换之前，作者使用乘法替换${}^{86}$来避免出现零值。
$$\mathrm{clr}\left(w\right)=\left\{\log \frac{w_0}{g\left(w\right)},\log \frac{w_1}{g\left(w\right)},\dots ,\log \frac{w_{C-1}}{g\left(w\right)}\right\}\text{ where }g\left(w\right)={\left(\prod _{i=0}^{C-1}{w}_i\right)}^{1/C}$$

---

2-6：评估与编码

为了训练自监督模型，作者从所有1021个LUAD和LUSC的TCGA全切片图像中随机选择了678张切片，未使用纽约大学队列的数据。

此外，作者从这些选定的全切片图像中对$250\mathrm{K}$的$583\mathrm{K}$切片进行了二次采样。一旦自监督模型训练完成，作者将其冻结并用于将组织切片投影到表示中。

为确保二次采样不会影响性能，在训练后还使用完整的未二次采样的训练队列（并使用与Chen等人${}^{30,38}$中类似的5折交叉相关分割）进行了LUAD生存分析任务。

作者在训练过程中跟踪模型的训练损失和验证损失，以确保没有过拟合。作者发现两个损失同时收敛且没有过拟合（补充图30）。

---

对于作者的肺腺癌和鳞状细胞癌分类分析，作者执行以下步骤。

作者设置了5折交叉验证，并且为了进一步防止特定部位的偏差${}^{43}$，作者以一种在TCGA训练集、验证集和测试集之间获得不重叠机构的方式来进行。

对于每一折，作者基于TCGA训练集的表示定义莱顿聚类，并根据在训练集中找到的聚类（即HPC）将聚类分配给TCGA验证集和测试集的表示。纽约大学的队列也被用作一个额外的外部测试集，并将那些HPC分配给它。

随后，作者使用来自训练集的全切片图像向量表示拟合逻辑回归，并在TCGA验证集和测试集以及纽约大学队列上评估性能。这个过程背后的动机是确认该方法对于不同机构的不同成像过程具有鲁棒性，保持一致的性能。这些结果可以在补充图31中找到。

一旦作者确定不同训练集上的HPC提供了相似的性能，作者锁定了一个特定的聚类配置，并使用它来评估逻辑回归在5折交叉验证中的性能。作者使用这个过程以便聚类在各折之间是相同的，并且作者可以评估它们对预测肺腺癌或鳞状细胞癌的影响。

---

作者使用SHAP（SHapley加性解释）来评估一个HPC对每个患者对数优势比的影响。

作者在5折交叉验证的每个测试集上计算SHAP值（补充图16D）。这种方法使作者能够检查HPC贡献值与其对各折对数优势比的影响之间关系的一致性；HPC值（红色/蓝色强度）及其与模型输出的关系在各折之间应该是相似的。

作者使用这种方法而不是为每个系数绘制森林图，因为作者的逻辑回归是L1范数惩罚的，并且对于惩罚回归，系数的置信区间可能会过于乐观${}^{87-89}$。

此外，作者不评估切片数量少于100的全切片图像；作者做出这个选择是为了确保作者从组织切片中获得足够的HPC分配。这个操作导致不评估3.8%（39/926）的全切片图像。

---

在进行LUAD总生存期分析时，作者遵循类似的流程，为保持一致性进行了单独的独立聚类。

作者使用TCGA数据集设置了5折交叉验证，将其分为训练集和测试集，并将纽约大学（NYU）作为额外的独立测试集。

由于样本数量有限，并且为了使各折数据平衡，在这种情况下，作者没有考虑TCGA验证集或非重叠机构。对于每一折，作者基于TCGA训练集的表示定义高预后簇（HPC），并根据在训练集中找到的HPC将其分配给TCGA测试集和纽约大学数据集的表示。

之后，作者使用Cox比例风险回归对总生存期进行建模，使用来自训练集的全切片图像（WSI）向量表示来拟合模型，并在TCGA测试集和纽约大学数据集上评估性能。

与肺型分类的情况一样，这种方法的目的是表明即使在跨不同训练集进行聚类时，该方法也是稳健的。这些结果可在补充图31中找到。

然后，作者锁定一种特定的聚类配置，以**找出哪些高预后簇（HPC）会影响Cox模型中总生存期的预测。**作者使用SHAP来评估每个高预后簇（HPC）对每个患者对数风险比的影响。作者在5折交叉验证的每个测试集上计算SHAP值（图6）。

作者使用这种方法而不是森林图，因为作者的Cox比例风险模型是L2范数惩罚的，并且惩罚回归系数的置信区间可能会过于乐观。

此外，作者不评估切片数量少于100的患者；作者做出这个选择是为了确保从组织切片中获得足够的高预后簇（HPC）分配。此操作导致不评估6.5%（28/442）的TCGA患者和2.9%（8/276）的$NY{U}_1$患者。

---

在作者的LUAD无复发生存期分析中，作者对纽约大学队列使用了5折交叉验证。在这种情况下，作者使用与总生存期的TCGA训练集定义的相同高预后簇（HPC）。

最后，作者使用在总生存期分析中选择的相同聚类配置。这使作者能够关联高预后簇（HPC）在无复发生存期和总生存期方面的影响。

作者再次使用SHAP来评估每个高预后簇（HPC）对每个患者对数风险比的影响；在5折交叉验证的每个测试集上计算值（图6C）。

高风险组和低风险组由训练集风险预测的中位数定义。该中位数随后用于划分测试集和额外独立集的风险组。作者使用对数秩检验来衡量风险组之间的统计学显著性，并使用$p$值阈值0.05。

---

对于作者的多癌种总生存期分析，作者直接使用患者的高预后簇（HPC）贡献来对风险进行建模并计算一致性指数（c指数）。

这种方法不需要任何参数拟合，计算出的c指数可以解释为与死亡事件相关的高预后簇（HPC）（c指数 $>0.5$）或与生存相关的高预后簇（HPC）（c指数 $<0.5$）。

对于每种癌症类型，作者通过将患者全集划分为5个大小相等或相似的不同集合，并在每个集合中评估c指数，进行了5折交叉验证。

在补充图23中，作者展示了每种癌症类型在5折交叉验证中c指数值的平均值和95%置信区间。此外，作者只显示高风险组和低风险组的对数秩检验显著（$p$值 $<0.05$）时的c指数值。

代码是用Python编写的，深度学习模型是在TensorFlow中实现的。

作者使用了ScanPy ${}^{91}$ 中的Leiden ${}^{48}$ 和PAGA ${}^{90}$ 算法实现、Lifelines ${}^{92}$ 中的Cox比例风险和Kaplan-Meier模型、SciPy ${}^{93}$ 中的统计检验（Fisher精确检验、超几何检验和Kolmogorov-Smirnov检验）以及statsmodels ${}^{94}$ 中的逻辑回归实现。

---

2-7：聚类特征

通过Spearman等级相关性分析，对每位患者的HPC（以每位患者的HPC百分比的中心对数比表示）和免疫图谱特征（免疫特征表达）进行相关性分析。

首先，构建患者向量表示，其维度等于HPC的数量，其中每个维度描述一个HPC对总组织面积的百分比贡献。其次，通过乘法替换（$1/$的增量（数字$\mathrm{HPC}{)}^2$，以避免零值）和中心对数比变换对患者向量表示进行归一化。

这使得每位患者对于每个免疫特征表达都有一个连续值（例如，肿瘤浸润淋巴细胞区域分数范围为0至35）。对于每对HPC和免疫特征，作者对所有患者进行Spearman相关性分析。

显著性阈值设置为调整后的$p$值的0.01，并且通过Benjamini/Hochberg错误发现率方法${}^{95}$对$p$值进行多重比较调整。结果如图7A所示。

---

通过计算每种癌症类型的相关性平均值，报告了多癌种HPC与免疫图谱特征的相关性。通过Fisher联合概率检验合并各癌症类型的P值，显著性阈值设置为0.01。结果如图9A所示。

为了检查每个HPC的组织切片中细胞类型的富集和耗竭情况，作者使用Hover-Net ${}^{55}$来估计肺腺癌$NY{U}_1$队列中每个切片的肿瘤、结缔组织、炎症和死亡细胞的数量。

这些注释使作者能够测量每个HPC以及整个切片群体中每个切片的细胞类型数量分布。作者通过测量整个切片群体与分配给特定聚类的切片之间的分布偏移，来测量每个HPC中每种细胞类型的过度和不足表示。

作者使用双样本Kolmogorov-Smirnov（K-S）检验来解释这种分布偏移，并使用K-S统计量$D_{n,m}$来量化过度表示和不足表示，如果存在过度表示则赋值$+D_{n,m}$，如果存在不足表示则赋值$-D_{n,m}$。双样本Kolmogorov-Smirnov检验使用统计量$D_{n,m}$来量化经验累积分布之间的距离。该统计量定义为$D_{n,m}=\underset{x}{\sup }\left|F_{1,n}\left(x\right)-F_{2,m}\right|$，其中$F_{1,n}\left(x\right),F_{2,m}$是第一个和第二个样本的经验累积分布函数，$n$是$F_1,m$的样本大小，$F_2$是$F_2$的样本大小，$x$是两个分布的支持集。

显著性阈值设置为调整后p值的0.01，并且通过Benja-mini/Hochberg错误发现率方法${}^{95}$对p值进行多重比较调整。结果如图7B所示。

在补充图32中可以找到过度和不足表示的示例以及它如何转化为统计量$D_{n,m}$。

---

此外，作者测量了每个HPC的肺腺癌亚型（如实体型、腺泡型、乳头型、微乳头型和鳞屑型）的富集情况（图7A - C）。

肺腺癌$NY{U}_1$队列包含3位病理学家对这些组织学亚型的手动注释（使用ImageScope软件在每张幻灯片级别完成；Aperio Technologies，Vista，加利福尼亚州，美国），并且作者将手动区域注释转换为单个切片注释（如果该区域与切片的重叠超过$50\%$，则为每个切片分配病理学家绘制的区域的标签）。

通过使用超几何检验将每个HPC与注释切片的整个群体进行比较来测量亚型富集情况。

---

超几何检验使用超几何分布来衡量在从大小为$N$且有$K$次成功的总体中无放回地抽取$n$次时出现$k$次成功的统计显著性。

在作者的案例中，作者将$k$指定为具有特定组织学亚型的切片数量，HPC中的切片总数为$n,K$，$n,K$是在大小为$N$的注释切片总体中具有相同特定组织学亚型的切片数量。

作者使用一个定义为$k/\mathbb{E}\left[x\right]$的倍数指标来衡量富集情况，其中$\mathbb{E}\left[x\right]$是给定$n$时超几何分布的期望值，$K,N$。特定组织学亚型的富集显示为倍数$>1$，耗竭显示为倍数$<1$，作者对调整后的p值使用0.01的显著性阈值。通过Benjamini/Hochberg错误发现率方法${}^{95}$对p值进行多重比较调整。

关于作者如何使用超几何检验进行富集和耗竭分析的示例可在补充图33中找到。

---

2-8：簇的组织学评估

为LUAD定义的HPC由三位专科诊断组织病理学家（J.L.Q.、N.N.、D.M.）独立检查。

对于每个HPC，每个簇随机选择100个切片图像进行评估。每个切片在$5\mathrm{X}$倍放大率下的分辨率为$224\times 224$像素，覆盖大约$452\mu {\mathrm{m}}^2$的组织（每像素$2.016\mu \mathrm{m}$），基于之前的一项证明，即这样的分辨率和视野对于许多肺部分类目的来说是足够的 ${}^8$。

使用结构化数据收集工具对每个HPC进行形态学描述和分类。每个簇被分类为主要由含肿瘤的切片组成或不是。根据此分类，要求病理学家从一组选项中列出主要和第二主要特征（分别为肿瘤生长模式或非肿瘤成分）。

在任何一种情况下，病理学家都提供了关于淋巴细胞浸润（即浸润性TIL的数量）和坏死的信息，并被鼓励进行自由文本评论。这些专家注释被转换为共识度量，包括一致性得分。

一致性得分给出了就最丰富的模式或特征达成一致的病理学家数量（1 - 3）。小于3的值通常反映两种或更多外观以近乎相等的水平出现的情况，尽管在这种组织病理学判断中也存在相当大的差异。

为每个簇创建了一个简短的总结标题，总结了组织病理学意见并描述了HPC的总体主要外观。结果如图2D、3和4所示。

---

三、HPL系统概述

HPL能够在不需要专家注释或标签的情况下，自动发现病理切片中的鉴别性图像特征。该系统通过对图像块进行聚类来识别形态相似的组织区域，创建一个组织形态表型库，该库可以与组织学、分子和临床表型相关联。

3-1：系统架构

HPL采用模块化设计，具有不同的组件，这些组件处理来自全切片图像（WSIs）的数据，经过各个分析阶段。

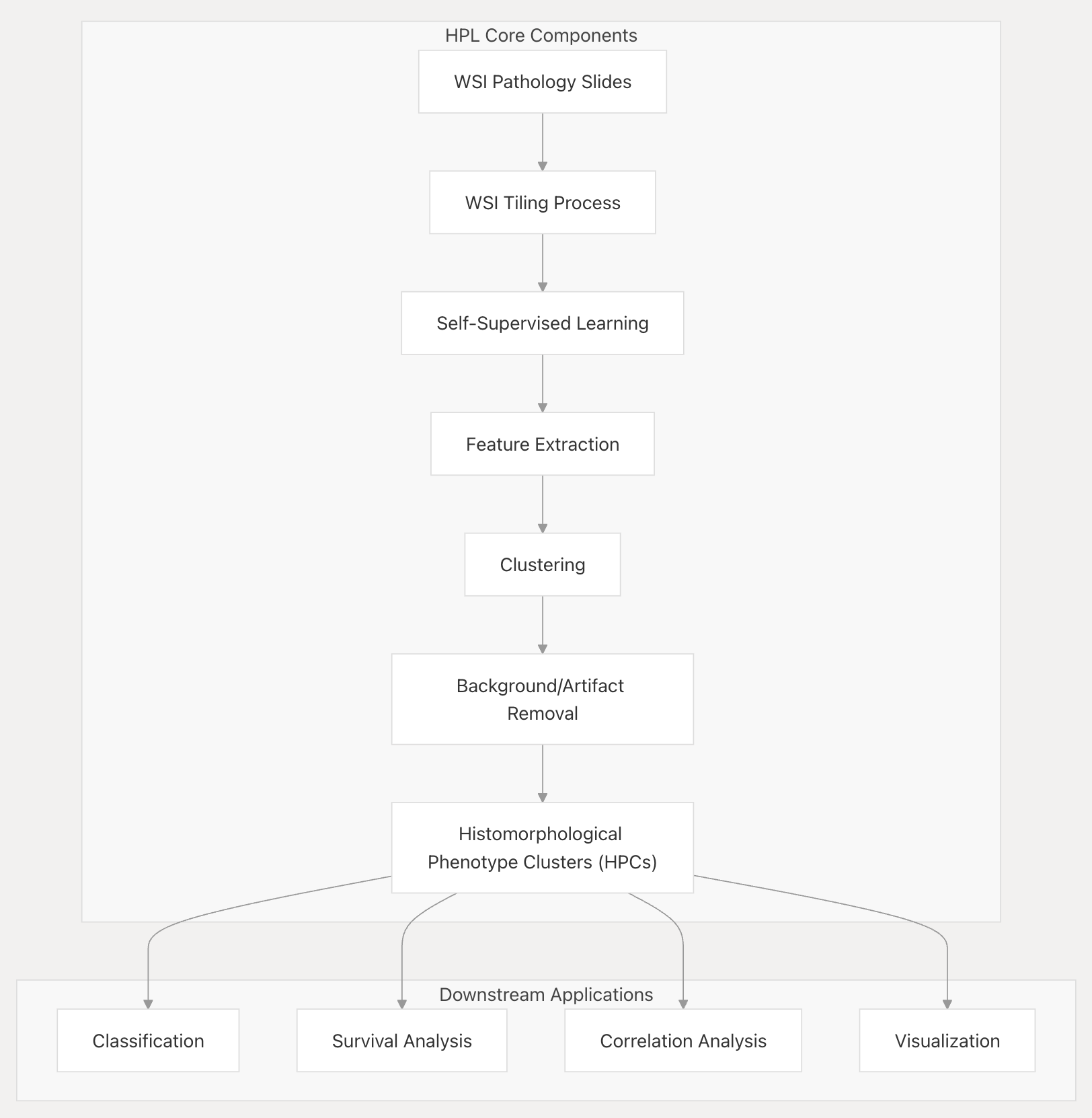
• 核心组件（HPL Core Components）相关：
  • 输入：WSI Pathology Slides（全切片成像病理切片 ）
  • 流程步骤：WSI Tiling Process（全切片成像切片处理 ）、Self - Supervised Learning（自监督学习 ）、Feature Extraction（特征提取 ）、Clustering（聚类 ）、Background/Artifact Removal（背景/伪影去除 ）
  • 输出：Histomorphological Phenotype Clusters (HPCs)（组织形态表型簇 ）
• 下游应用（Downstream Applications）：Classification（分类 ）、Survival Analysis（生存分析 ）、Correlation Analysis（相关性分析 ）、Visualization（可视化 ） ，呈现了从病理切片输入到表型簇输出及后续应用的完整HPL工作流 。

---

3-2：数据流

HPL系统通过一系列转换处理数据，从原始全切片图像到可量化的表型。

Raw WSIs（原始全切片成像 ）→ Tiled Images (H5)（切片图像，H5格式 ）→ Self - Supervised Model（自监督模型 ）→ Feature Vectors (H5)（特征向量，H5格式 ）→ Combined Feature Set (H5)（组合特征集，H5格式 ）→ Leiden Clustering（ Leiden聚类 ）→ Filtered HPCs（过滤后的组织形态表型簇 ）→ Downstream Analysis（下游分析 ） ，呈现从原始病理切片到下游分析的完整数据流转过程 。

---

3-3：关键组件

WSI切片过程

切片过程将大型全切片图像分成较小的224×224像素的图像块，并将它们存储在HDF5（H5）文件中。

这个初始数据处理步骤为所有后续分析奠定了基础。

组件	用途	输出
WSI切片	将全切片图像分成固定大小的图像块	带有图像和元数据的H5文件

---

自监督学习

HPL采用Barlow Twins这种自监督学习方法，从无标签的组织学图像块中学习有意义的表征。

该模型经过训练，可在无监督的情况下提取捕捉重要形态特征的特征。

---

特征提取

训练后，自监督模型用于从所有图像块中提取特征向量。这些特征向量捕捉每个组织区域的基本形态特征。

特征类型	维度	来源
潜在表征	128	模型编码器输出

---

Leiden聚类

使用Leiden聚类（一种用于网络中社区检测的算法）对特征向量进行分组。

这个过程识别出具有相似形态特征的图像块，并将它们分组到组织形态表型簇（HPCs）中。

---

背景去除

识别背景和伪影图像块并将其从分析中移除，以确保HPCs代表真实的生物结构。

---

下游应用

已识别的HPCs支持各种下游分析：

应用	描述	实现
分类	使用逻辑回归进行肺癌亚型分类	作为特征的HPCs
生存分析	使用Cox比例风险模型预测患者结局	作为预后标志物的HPCs
相关性分析	将HPCs与分子和临床表型联系起来	统计相关性
可视化	UMAP、聚类可视化和WSI叠加	交互式可视化工具

---

3-4：目录结构

HPL使用标准化的目录结构来组织数据、模型和结果。

---

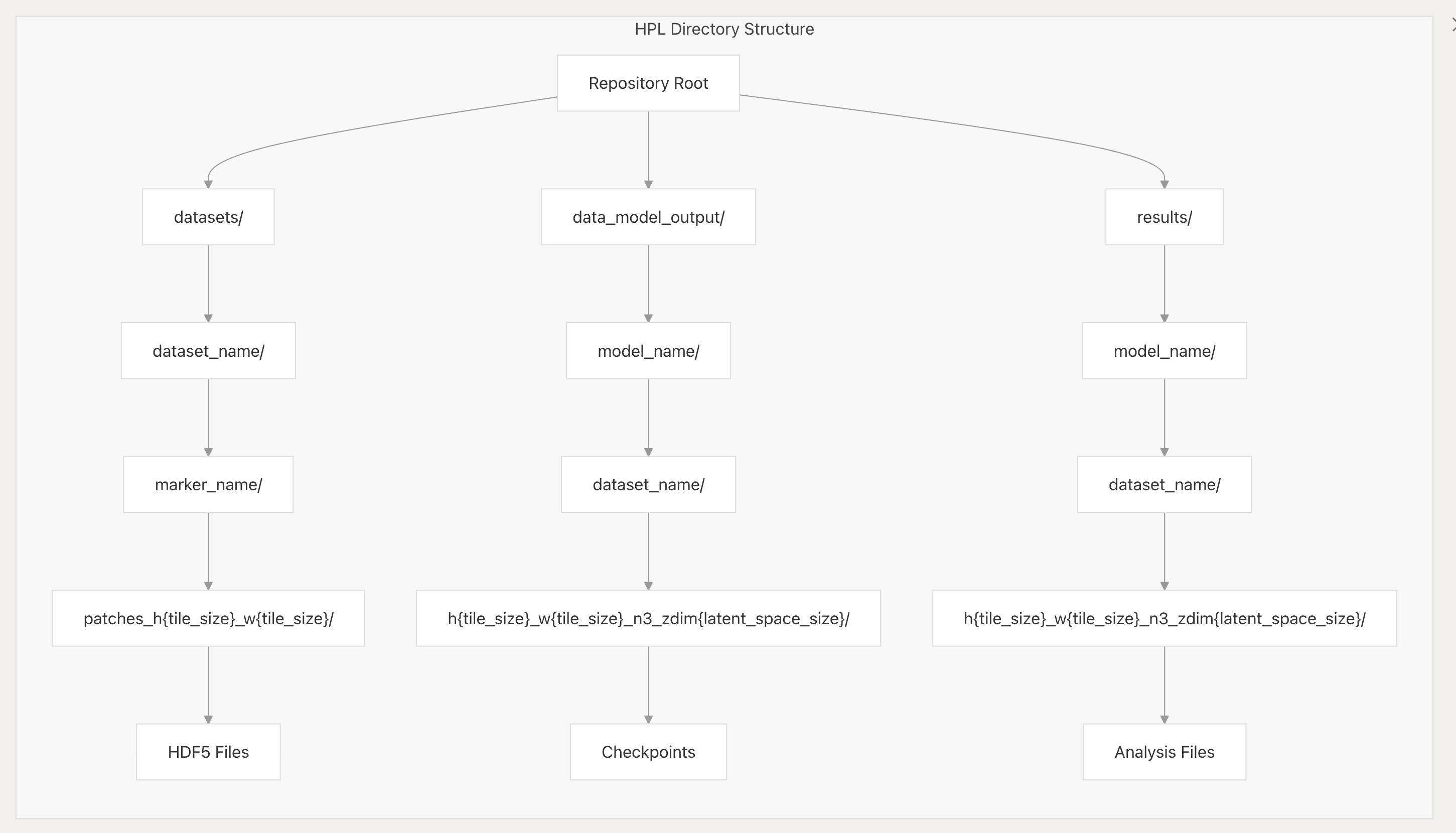
3-5：HDF5文件结构

HDF5文件是HPL工作流程的核心，并遵循标准化结构：

数据集名称	内容	维度
{set}_img	图像块	[样本数，高度，宽度，通道数]
{set}_tiles	图像块坐标	[样本数，2]
{set}_slides	切片标识符	[样本数，1]
{set}_samples	患者标识符	[样本数，1]
{set}_z_latent	特征向量	[样本数，潜在维度]
{set}_h_latent	隐藏表征	[样本数，隐藏维度]

---

3-6：核心技术

HPL依赖于几个关键技术和库：

技术	用途	版本
TensorFlow	深度学习框架	1.15
Scanpy	单细胞分析工具（用于聚类）	1.7-1.8
UMAP	降维	0.5.0
h5py	HDF5文件处理	3.4.0
Lifelines	生存分析	0.26.3
scikit-learn	机器学习工具	0.24.0

---

结束语

本期推文的内容就到这里啦，如果需要获取医学AI领域的最新发展动态，请关注小罗的推送！如需进一步深入研究，获取相关科研服务，欢迎扫码前往我们团队的主页！