波束形成基于对角加载的稳健自适应波束形成

量大龙神魔

已于 2023-11-25 16:48:50 修改

阅读量5.1k

点赞数 16

文章标签：矩阵线性代数算法 matlab

于 2023-03-19 20:57:48 首次发布

本文链接：https://blog.csdn.net/qq_45471796/article/details/129506971

版权

前言

本人刚刚入门阵列信号处理的波束形成方向，因此仿真过程中可能会出现错误，如果诸位大佬发现仿真过程中有错误，请不吝指出谢谢。

对角加载(Diagonal Loading, DL)是一种比较常用的提高Capon波束形成器鲁棒性的方法，通过在样本协方差矩阵的对角元素上加上一个适当的量，可以有效地提高样本协方差求逆(SMI)波束形成算法的稳健性，一般来说，通过在原样本协方差矩阵的基础上加上一个对角加载的量来更新矩阵，实现波束形成器的鲁棒性的方法都可以算作是对角加载法。在经典的对角加载法中，经过对角加载更新的矩阵一般可以定义为：

$LNR=10\lg \left ( \lambda/\sigma_w^2 \right )$

其中 $\sigma_w^2$ 为噪声中白噪声分量的功率， $\lambda$ 为对角加载量， $LNR$ 为加载噪声级，经验表明， $LNR$ 一般取10，由此可以通过噪声功率得到一个较为合适的对焦加载量，因此，根据MVDR的最佳权向量解，可以得到一个较为一般的对角加载波束形成器的权向量解：

$\hat{w}_{LSMI} = \frac{\left ( \hat {R}^{-1} + \lambda I \right )^{-1} \bar{a}_s}{\bar{a}_s^H \left ( \hat {R}^{-1} + \lambda I \right )^{-1} \bar{a}_s}$

早期的鲁棒自适应波束形成器大多可以以对角加载的形式表现出来，比如S. A. Vorobyov等人提出的最坏情况性能最优波束形成器(Worst-case Performance Optimization, WCPO),其等价权向量解为：

$\hat {w}_{WCPO} = \frac{ \lambda_{L} \left ( \hat {R} + \lambda_{L} \varepsilon ^{2} I \right ) ^{-1} \bar {a}_{s}}{ \lambda_{L} \bar {a}_{s}^{H} \left ( \hat {R} + \lambda_{L} \varepsilon ^{2} I \right ) ^{-1} \bar {a}_{s} -1}$

关于这篇文章可以参考YHCANDOU大佬的最差性能最优波束形成算法。

问题的提出与作者的解决方案

在这篇文章中，作者分别考虑了样本协方差矩阵满秩(快拍数大于阵元数)与欠秩(快拍数小于阵元数)两种情况。

对于满秩的情况，作者提出了一个约束来获得导向矢量，该约束可以表示为：

$\max_{\sigma^2, a} \sigma^2,s.t. R- \sigma^2aa^{*} \geq 0,\left ( a - \bar {a} \right )C^{-1}\left ( a - \bar {a} \right )\leq 1$

其中 $\bar a$ 为已知的名义导向矢量， $C$ 为一给定的正定阵，然而在一般情况下， $C= \epsilon I$ ，因而该约束问题可以化为一个球形约束下的二次优化问题，即：

$\min_{a} a^{*} R^{-1} a,s.t. \left \| a-\bar {a} \right \|\leq \epsilon$

对于该优化问题，可以采用CVX求解器进行求解，此处作者采用了拉格朗日乘子法进行解决，构造拉格朗日函数：

$f = a^{*}R^{-1}a+\lambda\left ( \left \| a-\bar {a} \right \| ^{2} -\epsilon\right )$

对 $a$ 求导并令其导数为0，即得：

$R^{-1}\hat {a}_0+\lambda \left ( \hat {a}_0 - \bar {a}\right ) = 0$

化简即得(通过Woodbury矩阵反演公式)：

$\hat {a}_0 = \left ( \frac{R^{-1}}{\lambda} \right )^{-1} \bar {a} = \bar {a} - \left ( I+\lambda R \right )^{-1} \bar {a}$

则

$\bar {a}-\hat {a}_0=\left ( I+\lambda R \right )^{-1} \Rightarrow \left \| \bar {a}-\hat {a}_0 \right \|=\left \| \left ( I+\lambda R \right )^{-1} \right \|$

定义

$g\left ( \lambda \right ) \triangleq\left \| \left ( I+\lambda R \right )^{-1} \right \|^{2} = \sum_{m=1}^{M} \frac{\left | z_{m} \right | ^{2}}{(1+\lambda \gamma_{m})^{2}}= \epsilon$

则可通过牛顿法对该方程的 $\lambda$ 进行迭代求解。

最后的估计得到的导向矢量 $\hat {a}_{0}$ 即为：

$\hat {a}_{0} = \bar {a} - U\left ( I+\lambda \Gamma \right ) ^{-1} U^{*} \bar {a}$

该情况下得到的权向量 $\hat {w}_{0}$ 为：

$\hat {w}_{0} = \frac{\left ( R+\frac{1}{\lambda} \right ) ^{-1} \bar {a}}{\bar {a}^{*}\left ( R+\frac{1}{\lambda} \right ) ^{-1} R \left ( R+\frac{1}{\lambda} \right ) ^{-1} \bar {a}}$

对于欠秩的情况，作者构造了以下的约束来获得导向矢量：

$\max_{\sigma^2, a} \sigma^2,s.t.a=Bu+\bar {a},,\left \| u \right \| \leqslant 1$

其中B是一个 $M \times L$ 的矩阵，且 $L< M$ ,该矩阵为列满秩，构成该矩阵的 $L$ 个列向量分别为其他角度上的名义导向矢量或者其线性组合，而 $u$ 则为各自列向量分量的系数。

和上一种情况的优化问题转换方式一样，该优化问题可以转换为：

$\min _{u} \left ( Bu+\bar {a} \right ) ^{*} R ^{-1} \left ( Bu+\bar {a} \right ) ,s.t.\left \| u \right \| \leqslant 1$

又因为在这种情况下阵列协方差矩阵存在欠秩的情况，所以作者在这里对协方差矩阵进行了降秩的操作以保证变换后的协方差矩阵的满秩性，令：

$\check {R} = B^{*}R^{-1}B, \bar {\check {a}} = B^{*}R^{-1}\bar {a}$

该优化问题即为：

$\min _{\check {a}} \check {a} ^{*} R ^{-1} \check {a} ,s.t.\left \| \check {a}-\bar {\check {a}} \right \| ^{2}\leqslant 1$

对该优化问题的近似求解过程与上一节方法类似，当然，该优化问题也可以用CVX求解器进行快速求解。

阵列权向量为：

$w = \frac{\hat R_{-1} \hat a_0}{\hat a_0^H \hat R^{-1} \hat a_0}$

仿真

部分仿真条件如下所示：

阵元数	10
信噪比	0
扰噪比	20
阵元间距	半波长
信源数	1
干扰数	2
信源到达角	5°
干扰到达角	-30°，45°
信源角度估计误差	[0°,4°]
不确定系数 $\epsilon$	4.5

clc;
clear;
jk = 0;
loop = 50;
SINRO = zeros(1,length(-20:5:40));
snr = 0;
deg_dev_predf = 4;%%预定义的角度最大偏移量
%% 初始化及设定参数
array_num = 10;%%阵元数
snapshot_num = 40;%%快拍数
source_aoa = [5,-30,45];%%信源到达角
tgt_ang = 1;
c = 340;%%波速
f = 1000;%%频率
lambda_wave = c/f;%%波长
d = 0.5*lambda_wave;
inr1 = 20;
inr2 = 20;
source_num = length(source_aoa);%%信源数
sig_nr = [snr,inr1,inr2];%%信号功率dBw
deg_deviate = 2;%%误差角度偏离
source_dev = source_aoa(tgt_ang)+deg_deviate;
epsl = 4.5;
%% 转向矢量
a_bar = exp(-1i*(0:array_num-1)'*pi*sind((source_aoa(tgt_ang)+deg_deviate)));%%实际带有误差的阵列响应矢量
A = exp(-1i*(0:array_num-1)'*2*pi*(d/lambda_wave)*sind(source_aoa));%%阵列响应矩阵
a_real = A(:,1);
tar_sig = wgn(1,snapshot_num,sig_nr(tgt_ang));
inf1 = wgn(1,snapshot_num,sig_nr(2));
inf2 = wgn(1,snapshot_num,sig_nr(3));
n = (randn(array_num,snapshot_num)+randn(array_num,snapshot_num)*1i)/sqrt(2);
rec_sig = A(:,1)*tar_sig+A(:,2)*inf1+A(:,3)*inf2+n;
R = rec_sig*rec_sig'/snapshot_num;%%接收阵的协方差矩阵
if array_num < snapshot_num
    R_inv = inv(R);
    Rs = A(:,1)*tar_sig*(A(:,1)*tar_sig)'/snapshot_num;
    Ri = (A(:,2)*inf1+A(:,3)*inf2)*(A(:,2)*inf1+A(:,3)*inf2)'/snapshot_num;
    Rn = n*n'/snapshot_num;
    [U,Gamma,V] = svd(R);
    Gamma_vec = diag(Gamma);
    z = abs(U'*a_bar);
    lambda = 0;
    while abs(norm(z./(1+lambda*Gamma_vec))^2-epsl)>1e-5
        lambda = lambda+(norm(z./(1+lambda*Gamma_vec))^2-epsl)/ ...
        sum(2*z.^2.*Gamma_vec.*(1+lambda*Gamma_vec)./(1+lambda*Gamma_vec).^4);
    end
    a_est = a_bar-U*diag(1./(1+lambda*Gamma_vec))*U'*a_bar;
    w0 = inv(a_est'*inv(R)*a_est)*inv(R)*a_est;
else
    R_inv = inv(R);
    Rs = A(:,1)*tar_sig*(A(:,1)*tar_sig)'/snapshot_num;
    Ri = A(:,2)*inf1*(A(:,2)*inf1)'/snapshot_num;
    Rn = n*n'/snapshot_num;
    degr(ik,:) = linspace(source_dev(ik)-deg_dev_predf,source_dev(ik)+deg_dev_predf,array_num-1);
    B = exp(-1i*(0:array_num-1)'*2*pi*(d/lambda)*sind(degr(ik,:)));
    R1 =  B'*inv(R)*B;
    a1 = B'*inv(R)*a_bar;
    [U,Gamma,V] = svd(R);
    Gamma_vec = diag(Gamma);
    [Gamma_vec,index_vec] = sort(Gamma_vec,'descend');
    U = U(:,index_vec);
    z = abs(U'*a1);
    if abs(norm(inv(R1)*a1)) <=1
        lambda = 0;
    else
        while abs(norm(z./(1+lambda*Gamma_vec))^2-1)>1e-5
            lambda=lambda+(norm(z./(1+lambda*Gamma_vec))^2-1)/ ...
            sum(2*z.^2.*Gamma_vec.*(1+lambda*Gamma_vec)./(1+lambda*Gamma_vec).^4);
        end
    u_hat = -1*U*inv(Gamma+eye(length(Gamma)))*U'*a1;
    a_est =  B*u_hat+a_bar;
    w0 = inv(a_est'*inv(R)*a_est)*inv(R)*a_est;
    end
end
beam_plot(w0);
 
function [] = beam_plot(input_weight_vector)
array_num = length(input_weight_vector);
theta = -90:0.01:90;
p = exp(-1j*2*pi*(0:array_num-1)'*sind(theta)/2);
y = input_weight_vector'*p;
outputval = 20*log10(abs(y)/max(abs(y)));
figure()
plot(theta,outputval);
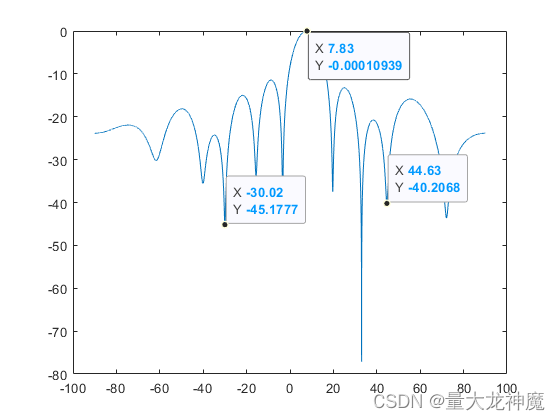
end

仿真运行结果如下图所示：