补码的符号位为什么能参与运算（看这一篇就够了，绝对通俗易懂！！！）

最新推荐文章于 2022-11-07 19:35:40 发布

置顶呆码农梦中识bug，程序员哭求加工资

最新推荐文章于 2022-11-07 19:35:40 发布

阅读量1.6w

点赞数 193

分类专栏：其他知识文章标签：计算机组成原理二进制原码，反码，补码基本原理电子技术基础

本文链接：https://blog.csdn.net/qq_45472866/article/details/114779170

版权

其他知识专栏收录该内容

4 篇文章 2 订阅

订阅专栏

补码 = 反码 + 1 为何成立（针对负数）

前置知识

补码的定义：

所谓补码，英语里又叫two's complement（对2求补），这个2指的是计数系统的容量（模），就是计数系统所能表示的状态数。比如 "1位符号位 + 4位数值位"，那么容量（模）就是 $2^{5}$

因为非负数是[0, $2^{4}$ - 1], 负数是[ - $2^{4}$ + 1, 0), 然后还有一个 -0，一共就是 $2^{5}$ 个；或者“暂时抛弃符号位”这一说法，5位二进制数表示的数最多就是 $2^{5}$ 个

因此，[x]补 = ( $2^{5}$ + x) % $2^{5}$ %x <=> 模x

反码的定义：

所谓反码，英语里又叫ones' complement（对1求补），这里的1，本质上是一个有限位计数系统里所能表示出的最大值，在8位二进制里就是11111111，在1位十进制里就是9，在3位十六进制里就是FFF（再大就要进位了）。求反又被称为对一求补，用最大数减去一个数就能得到它的反，很容易看出在二进制里11111111减去任何数结果都是把这个数按位取反，0变1，1变零，所以才称之为反码

因此，[x]反 = ( $2^{5}$ - 1 + x) % ( $2^{5}$ - 1)

这是计算反码的两个例子：

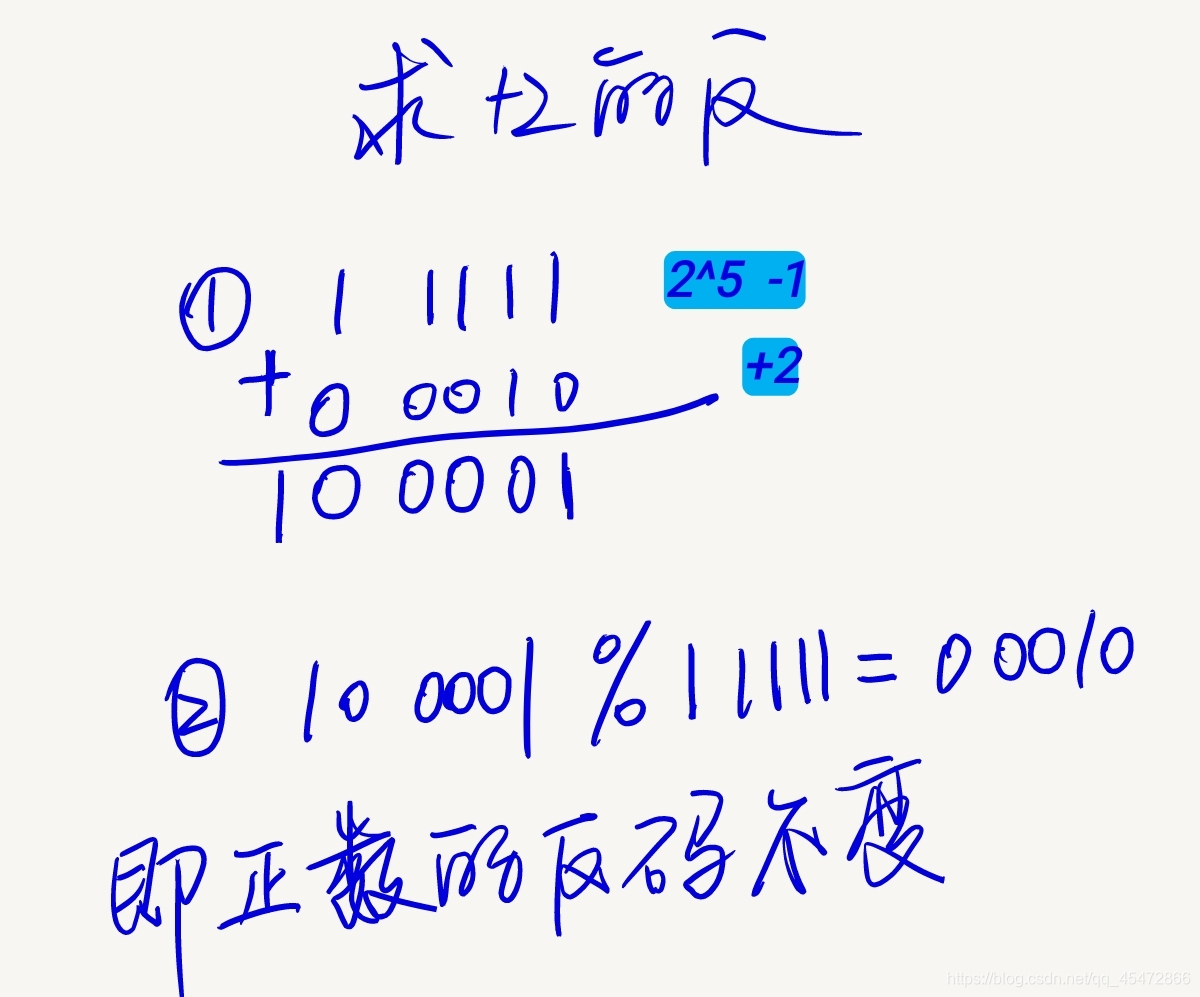
补码 = 反码 + 1 为何成立（针对负数）

由上，

[x]补 = ( $2^{5}$ + x) % $2^{5}$

[x]反 = ( $2^{5}$ - 1 + x) % ( $2^{5}$ - 1)

可推出，补码 = 反码 + 1 成立

补码 = 反码 + 1 只是一种求补码的方式，并不是定义，是由补码和反码的定义推出来的

步入正题

补码的意义

由上可知，[x]补 = ( $2^{5}$ + x) % $2^{5}$

推广到一般，就是 [x]补 = ( $2^{n + 1}$ + x) % $2^{n + 1}$ (n是数值位的位数)

拿经典的钟表为例

假设时针现在指在了3点的位置，我要让指针指向12点，那么我有两种选择（如果规定逆时针为负）

1、逆时针转3格（-3）

2、顺时针转9格（+9）

那么，-3和+9就起到了相同的作用，二者效果一样，都是从3点到12点

那么二者有什么关系呢？

其实二者互为补码（%12） 12恰好是计数系统的容量（即钟表最多表示12个数）

那么在 %12 的情况下，9 就可以 "代替 -3" 运算

如（8 - 3）% 12 = 5 % 12 = 5 (8 + 9) % 12 = 17 % 12 = 5

所以，补码的用处就是： 减一个数等价于加上这个负数的补码

那么就不用进行减法运算了，只要会加法就行

因此，补码的意义就是把负数变成它“对应的正数”，然后参与运算

为何补码的符号位能参与运算

首先，放上结论：补码根本就没有符号位

至于为什么，且听我细细道来！！

根据上面的推导可知，补码就是把负数转换成正数然后参与运算

也就是说，补码都是正数（敲黑板~~~）

都是正数，那么就没有必要区分正负了啊，也就不需要符号位了，所以补码没有符号位

拿-2为例

[-2]原 = 1 0010 [-2]补 = 11110

如我所说，没有符号位，那么11110就是30，也就是说 -2的补码是30 (% $2^{5}$ )，这显然是正确的，因此我上面的结论是正确的（自导自演了，哈哈哈哈）

因此，补码既然都没有符号位（都是数值位，最高位也是），那拿来运算就是理所当然的啦！！！

为何补码的最高位经常“被称作”符号位呢？

正数的补码等于其本身，那么补码的最高位自然就是0

计算负数的补码时

用这个公式：[x]补 = ( $2^{5}$ + x) % $2^{5}$

计算得到的补码最高位刚好为1

所以，事实情况是

补码的最高位和原码的符号位（最高位）是一样的

我们知道，补码是看不出一个数的真实值的，需要转换成原码才能计算出

现在又有了，补码的最高位和原码的最高位一样，而原码的最高位又表示正负

因此，就可以拿补码的最高位快速判定一个数的正负

然后，可能就有人发现了这个“巧合”，但是又不明白原理，就把补码的最高位当作符号位了，然后就给我们这些小白留下了无尽的困惑（QWQ）

总结一句话就是：补码的最高位能起到显示正负的功能（只是能起到符号位的功能），但不是真正的符号位，而是如假包换的数值位

总结

一定要从定义出发，搞清楚因果关系，由因 -> 果；如果搞不明白，就很容易弄混淆了，然后开始怀疑人生？（我可是乱说的啊，hhh）

我在大一下学期上那个电子技术基础的时候，还在课堂上讲过这些（还得感谢梁老师给的机会，哈哈哈），其实那时候也是半懂的状态给大家讲，也不知道其他同学有没有听明白（逃~）；然后这学期学计组，又遇到了这个难题（自我觉得很难！！）。反正总是要弄明白的，逃也逃不掉，所以花了两三天的时间，上网搜了很多别人的讲解，然后综合一下，自己再加以思考，结果就是理解的更深刻了，思路也更清晰了；至少现在，如果有人问我这个问题，我能面对面地把这个问题给他(她？)讲明白

仅仅在逻辑上给出证明而不能从直观上把握感知的话，证了也白证，心里还是很慌觉得知识不属于我 ---华为某大佬

作为一个工科生，基本的数学原理是需要搞明白的，不然总会觉得不舒服 ----交大某大佬

最后

这篇blog应该是我花的时间最多的啦，差不多4h?

我所理解的，都在这篇文章里面了，如果有错误的地方，欢迎指正！！！！

如果能帮到你，不妨给个赞👍？（逃~

呆码农梦中识bug，程序员哭求加工资

关注

193
点赞
踩
322

收藏

觉得还不错? 一键收藏
40
评论
补码的符号位为什么能参与运算（看这一篇就够了，绝对通俗易懂！！！）

前置知识补码的定义：所谓补码，英语里又叫two's complement（对2求补），这个2指的是计数系统的容量（模），就是计数系统所能表示的状态数。比如 "1位符号位 + 4位数值位"，那么容量（模）就是因为非负数是[0, - 1], 负数是[ -+1, 0), 然后还有一个 -0，一共就是个；或者“暂时抛弃符号位”这一说法，5位二进制数表示的数最多就是个因此，[x]补 = ( + x) % %x <=> 模x反码的...
复制链接

扫一扫