MODA 多目标蜻蜓算法

Nicer0815

已于 2023-07-04 18:45:51 修改

阅读量1.8k

点赞数 1

分类专栏：智能优化算法

于 2022-07-24 12:17:56 首次发布

本文链接：https://blog.csdn.net/qq_45555061/article/details/125957861

版权

MODA算法多目标优化蜻蜓算法帕累托最优解密度计算

关键词由CSDN通过智能技术生成

智能优化算法专栏收录该内容

6 篇文章

订阅专栏

MODA 多目标蜻蜓算法

1、算法简介

多目标蜻蜓算法(The DA algorithm for multi-objective problems)与DA算法在同一篇论文中提出。其主要灵感源于自然界中蜻蜓的静态和动态群集行为，具有寻优能力强等特点。

1.1、前置知识点

MODA与DA大体一致，所以接下来的分析都是建立在DA之上。

2、算法原理

与DA一致：

该算法源于自然中蜻蜓动态和静态的智能群行为，对蜻蜓的飞行线路、躲避天敌及寻找食物等生活习性进行数学建模。

在动态群中，为获得更好的生存环境（migration），大量的蜻蜓集群朝着共同的方向进行远距离迁徙；
在静态群中，为寻找其他飞行猎物（fading），由小部分蜻蜓组成的各个小组，在较小的范围内来回飞行。

蜻蜓飞行过程中的局部运动与飞行路径的临时突变是静态群的主要特征。

在自然界中，蜻蜓的生活习性可以归纳为５类行为方式：分离、排队、结盟、寻找猎物和躲避天敌。

3、算法细节

3.1、DA到MODA的分析

先简单思考一下可能存在的问题：

由于多目标的性质，不同解决方案之间的不能直接比大小
MODA最终得到的应该是一个解集合
多目标优化器的最终目标是找到最准确的帕累托最佳解决方案（收敛），并在所有目标中具有均匀分布（覆盖率）

那么可以推出的结论：

DA迭代过程中更新猎物和天敌的方式不再适用（DA源码如下）
- if Fitness(1,i)<Food_fitness %寻找每次迭代的最小值
MODA需要维护一个解集库：archive（repository）

3.2、算法细节（基于DA）

总述：

算法维护了一个解集库：archive，其中存放每轮迭代中的Pareto最优解，关于进archive集合的原则，原文大概是这么说的：
- 被支配的不能进；支配别人的可以进；没被人支配的进；
archive的管理机制：
- 如果archive已满，则可以从人口稠密的段中删除一种或多种解决方案
  - 代码里作者根据Archive_mem_ranks（也就是密度大小！）轮盘赌删除

天敌选择机制：

初始化天敌的各维度适应度为-inf
每轮迭代的时候，对当前的N个蜻蜓先进行一次遍历，先找出支配能力最弱的那只蜻蜓坐标为天敌坐标；
人口稠密的段中删除的解决方案被选为天敌

    % Chose the archive member in the most population area as enemies
    % to improve coverage
    % 概率选取一个rank（相当于密度）较大的当作天敌
    % 注：这里的Archive_mem_ranks相当于密度
    index=RouletteWheelSelection(Archive_mem_ranks);
    if index==-1
        index=1;
    end
    Enemy_fitness=Archive_F(index,:);
    Enemy_pos=Archive_X(index,:)';

这里引用一张原论文的插图：

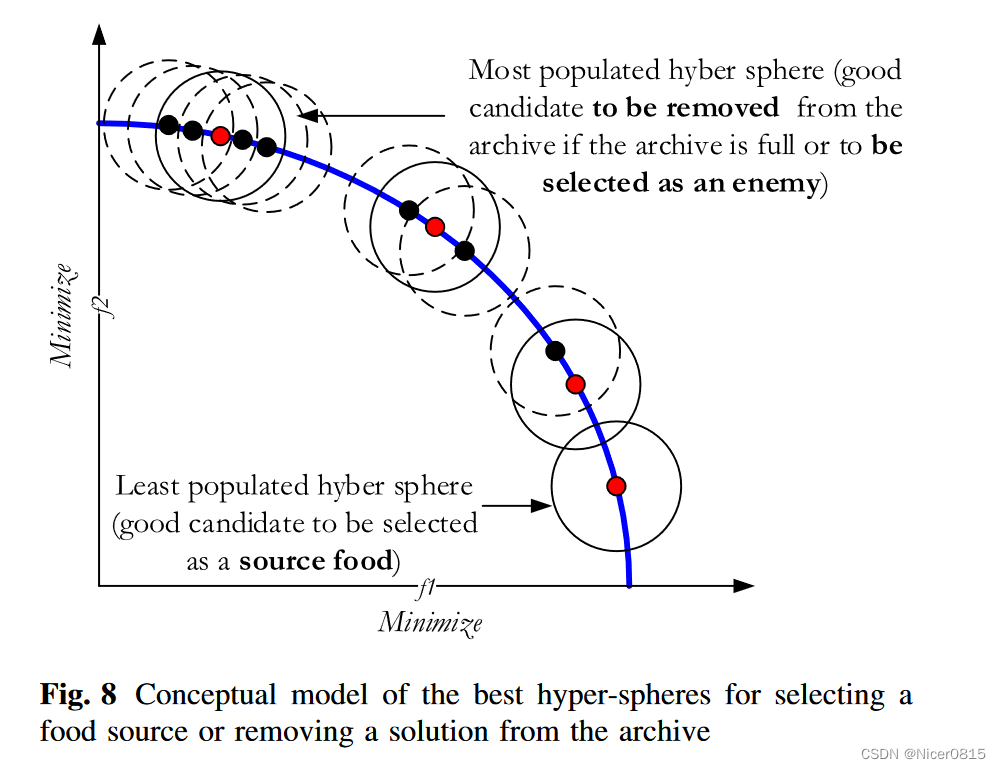
请添加图片描述

食物选择机制：
- 初始化食物的各维度适应度为inf
- 每轮迭代的时候，对当前的N个蜻蜓先进行一次遍历，先找出支配能力最强的那只蜻蜓坐标为食物坐标；
- 周围人口稀疏的解决方案被选为食物

    % Chose the archive member in the least population area as foods
    % to improve coverage
    % 取倒数 这样就rank（相当于密度）越小被选择的概率越大
    % 概率选取一个密度较小的当作食物
    index=RouletteWheelSelection(1./Archive_mem_ranks);
    if index==-1
        index=1;
    end
    Food_fitness=Archive_F(index,:);
    Food_pos=Archive_X(index,:)';

3.3、我之前的一些错误理解–关于密度

在此非常感谢我的大师兄帮我指出了理解上的误区！

主要是RankingProcess函数：

% 【错误理解】非支配排序 计算每个个体rank
% 【正确理解】统计密度 Archive_mem_ranks就是对应个体所在空间的密集程度
Archive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);

% 这个函数当时没仔细看QAQ
% 此rank非Pareto里的rank 而是指密度！
function ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no)

my_min=min(Archive_F);
my_max=max(Archive_F);

if size(Archive_F,1)==1
    my_min=Archive_F;
    my_max=Archive_F;
end
% 邻居半径划分为各维度的空间长度的1/20
r=(my_max-my_min)/(20);

ranks=zeros(1,size(Archive_F,1));
%采用类似NSGA-II中的密度计算方法
for i=1:size(Archive_F,1)
    ranks(i)=0;
    for j=1:size(Archive_F,1)
        flag=0; % a flag to see if the point is in the neoghbourhood in all dimensions.
        for k=1:obj_no
            % 第j个个体的第k个问题维度的坐标距离
            if (abs(Archive_F(j,k)-Archive_F(i,k))<r(k))
                flag=flag+1;
            end
        end
        % 如果所有维度距离都在对应的r(k)之内
        if flag==obj_no
            ranks(i)=ranks(i)+1; %密度++
        end
    end
end
end

4、算法流程

原文MODA算法流程伪码描述：（没啥好说的，跟代码一致，也很容易理解）

请添加图片描述

5、参考文献

[1]Mirjalili S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems[J]. Neural Computing and Applications, 2016, 27(4): 1053-1073.