群智能算法笔记——蚁群算法（ACO）

问题引入

Traveling salesman problem（TSP）
给定一组城市和每对城市之间的旅行成本，旅行者问题（简称 TSP）是找到访问所有城市并返回起点的最便宜的方式。 在我们研究的标准版本中，旅行成本是对称的，即从 X 城市到 Y 城市的旅行成本与从 Y 到 X 的旅行成本相同。(1) 旅行商问题 (TSP)

• P问题：可用多项式表达的问题
• NP问题：不可用多项式表达的问题（TSP为NP问题）
• NP问题不可求但可验证
  

问题分析

其中：

• C为N个城市集合
• L为任意连个城市c_i与c_j之间距离
• d为欧式距离算子
• 则TSP问题可以抽象为求D（x）最小值问题，D（x）中第一项为出发路径，第二项为返回路径

蚁群优化算法

步骤

其中：

• 步骤：1) 初始化参数 2）分配寻找 3）计算最短路径 4）更新信息素
• n ：城市数量
• m ：蚂蚁数量
• p：状态转换策略（单只蚂蚁选择路径概率）
• tao_ij（t+1）：信息素更新函数
• t_max：最大迭代次数

路径选择函数

其中：

• tao:信息素矩阵
• Tabu：路径记录
• n=1/D：启发函数，求解最短路径
• α：信息素参数，描述信息素权重
• β：启发函数参数，描述启发式函数权重

信息素更新函数

信息素更新后值为=残留值+信息素增量
其中：

• p：信息素挥发函数
• Q：信息素残留值
• 增量函数有三种模型：蚁周模型，蚁量模型，蚁密模型（蚁量模型，蚁密模型由于增量过大容易陷入局部最优解，故常用蚁周模型）

实例

用9只蚂蚁验证5个城市的TSP问题

STEP1：初始化参数

• 12345：表示5个城市坐标
  
• D为5个城市距离直积，即表示两两城市之间距离
• inf：无穷大
• 最大迭代次数取100
  
• tao：信息素残留矩阵，维度取决于城市数n
• Tabu：路径记录矩阵
  

STEP2：运行

• 随机将m只蚂蚁放置在n个城市上，放置方法：放置位置[m/n]*n（向上取整），本例中=10，则将1-10随机打乱取九个值置于Tabu出发城市。
  
• 以$P_{ij}^k$计算下一城市，首先计算{$P_{31}^1$，$P_{32}^1$，$P_{34}^1$，$P_{35}^1$}
• 根据$P_{ij}^k$公式可知其概率取决于信息素以及启发函数
  
  故第一只蚂蚁选择1城市概率最大，如果直接选择概率最大的则容易陷入局部最优，不能体现随机选择，故作以下处理
  
• 原概率过小故归一化便于后续操作
• 本例则蚂蚁1选择城市2为下一城市
  
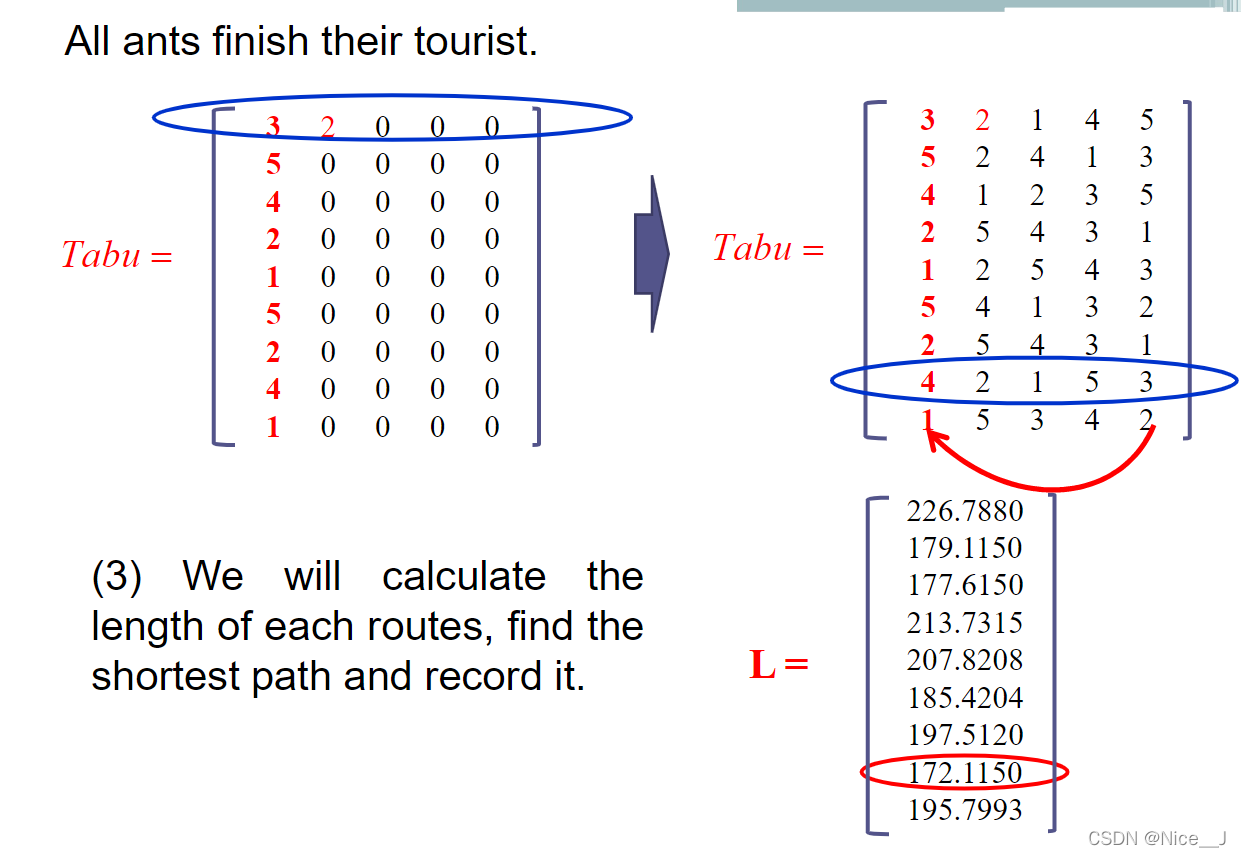
• 所有蚂蚁走完路径后构成完整TaBu表
• 计算每只蚂蚁总路径和构成L
• 本例蚂蚁8路径最小
  
• 本例选用的tao模型为蚁周型，则根据公式计算所有路径的信息素更新值
• 图中以3，4以及1，5路径为例，蚂蚁9从3返回4故也计入
  根据以上步骤则可获得最短路径，即最终所有蚂蚁都会走同一条路径。