数学分析 求极限的方法总结

极限是微积分中的基础概念，求极限是求函数的导数，微分，积分的重要前提条件，对于不同的函数或者数列，需要使用不同的方法求出或快速地求出极限。本文将总结求极限常用的各种方法。

1.数列求极限方法

首先给出数列极限的定义

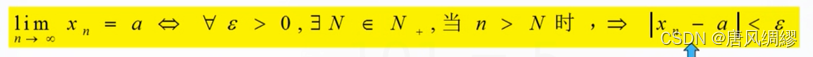
1. 1. 四则运算求极限

 

1.2  夹逼定理求数列极限

给出夹逼定理 证明略

可以得出夹逼推广

求解思想：缩放需要求的数列，得到两个极限相同的数列，从而通过夹逼定理得到原数列的极限，难点在于缩放找到两个极限相同的数列。

1. 1. 单调有界原理

1.3  函数极限与数列极限的关系

1.4 无穷大和无穷小

由此规律可以快速得到某些数列的极限

举例

1.5 重要数列极限

1.6 放缩求极限

1.7 stolz定理求极限

 

1. 函数求极限
   1. 函数极限的分类

单侧极限

此类问题通常使用极限定义求解

2.2.1四则运算求极限

同数列的方法

2.2.2分式求极限，极限由最高次项决定

2.2.3换元法求极限

2.2.4 重要极限

第一类重要极限

第二类重要极限

2.2.5连续函数极限符号换位

对于连续函数，函数符号和极限符号可以交换位置，这对求连续复合函数的极限很有用

                           举例……

2.2.6分母等于零的极限求法

2.2.7 洛必达法则

 

3. 总结

在求极限之前应当先通过如单调有界原理等方法确定极限是否存在以避免不必要的计算。数列，函数的求极限方法繁多，需要具体情况具体分析。通过不断地做题积累提高熟练度。