数学分析 第七章 定积分

定积分：分割近似求和取极限

定积分存在的必要条件：若f(x)在某域内可积，则它在该域内必有界

定积分存在的充分条件：

1. 若连续，则可积；
2. 单调有界函数必可积；
3. 有界，有限个间断点

尽量不要极限号和积分号换位

达布大和：将区间分成无数小区间，每个小区间的极大值记为M，△x为小区间的长度，达布大和S（T）=M△x的累加。达布大和是曲线外界多边形的面积

达布小和同理

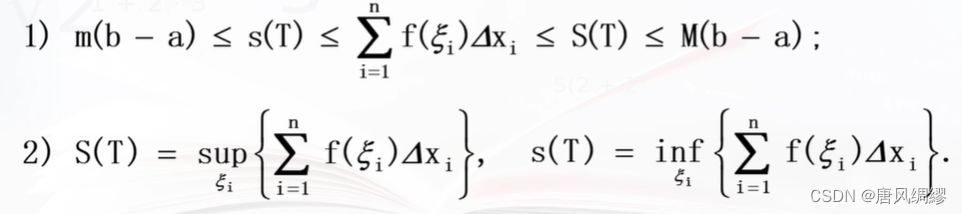
即便采用不同的分割，任一达布大和总是大于等于达布小和

所以：

达布定理：

定积分存在的充分条件

可积函数判别：

f(x)可积->f(x)的绝对值可积，平方可积。   反之不然

绝对值可积<-->平方可积   常用反例 ：  1，有理数-1，无理数

定积分第一中值定理：

注意：g(x)不能变号

例：

变限积分：

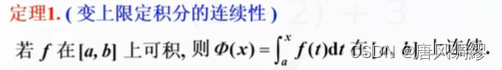
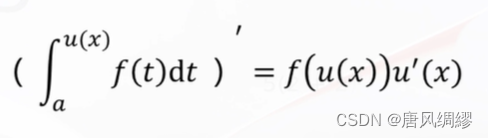注意：变上限积分的f中如果有自变量x,n那么不能直接求导                              例如上面这道题，直接求就错了

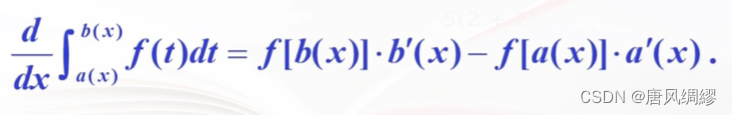
定积分与不定积分的关系

定积分存在不定积分不一定存在，反之亦然

例

cost^2有原函数（因为它连续）但不能用初等函数表示出来，所以不能求出它的积分结果（否则算错，属于混淆定积分与不定积分的概念）

定积分的换元积分法：

定积分的分部积分法使用前提

 使用分部积分时，积分上下限不变

                                 此题如果用这种方法就错了：

                              因为横线处没有用分部积分，积分上下限应该改变

分部积分yyds

做积分之前都应该先考虑能不能化简

施瓦兹不等式

积分应用：  求面积

求平面曲线弧长

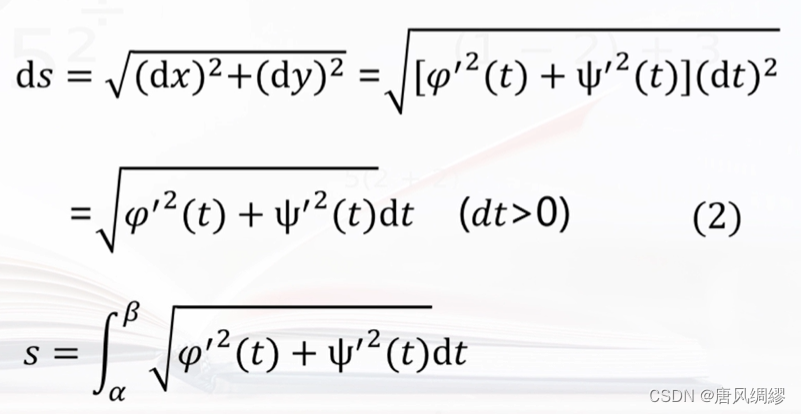
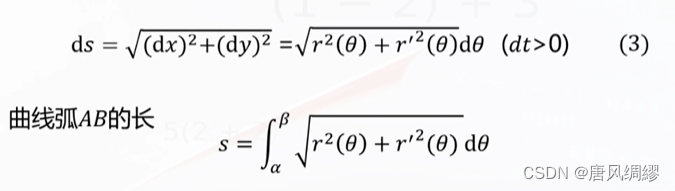
体积：