第七次讨论课个人资料-图的遍历

前言

图遍历又称图的遍历，属于数据结构中的内容。指的是从图中的任一顶点出发，对图中的所有顶点访问一次且只访问一次。图的遍历操作和树的遍历操作功能相似。图的遍历是图的一种基本操作，图的许多其它操作都是建立在遍历操作的基础之上。

写的我头都大了，坐着肝了10小时。

一、欧拉路径与欧拉环路

通俗地说，对于一个图的某条路径，如果能从一个点出发将这个图的所有边都不重复地走一遍，那么这条路径就被称为欧拉路，即小时候玩的一笔画问题;对于一个图的某条路径，如果能从一个点出发将这个图的所有边都不重复地走一遍并回到起点，那么这条路径就被称为欧拉回路。

1. 问题概述

1.1 定义

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。
如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。
具有欧拉回路的图称为欧拉图（简称E图）。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。

1.2 约定

1. 定义 $(A,B)$ 表示从 $A\to B$ 的一条边（若无特别说明，即为无向边）
2. 定义 $(A,B)\to (C,D)$ 表示从 $A\to D$，经过 $(A,B),(C,D)$ 两条边的路径
3. 定义   \: 孤立点   \: 表示一个度为 0 的点
4. 定义   \: 奇顶点   \: 表示一个度数为奇数的点
5. 定义对于有向图 G ，将所有的有向边替换为无向边得到图 G 的基图，若图 G 的基图是连通的，则称图 G 是「弱连通图」。
6. $Stac{k}_a$ 表示标号为 $a$ 的栈。
7. 用 $Stac{k}_x=a]b]c]$ 表示 $Stac{k}_x$ 的层级结构，其中 $a$ 为栈顶， $c$ 为栈底。
8. $Foo\to Bar$ 表示 $Foo$ 里的元素 $Bar$ （表特指）

2. 求解算法思想

2.1 判定

1. 无向图欧拉回路的判定：图G为连通图，所有顶点的度为偶数。
2. 无向图欧拉路径的判定：图G为连通图，除有2个顶点度为奇数外，其他顶点度都为偶数。
3. 有向图欧拉回路的判定：图G的①基图联通，所有顶点的入度等于出度。
4. 有向图欧拉路径的判定：图G的基图联通，存在顶点u的入度比出度小1，v入度比出度大一，其余所有顶点的入度等于出度。（此时u即路径的起点，v即终点）
5. 无孤立点的有向图 G 为欧拉图，当且仅当图 G 弱连通且所有顶点的入度等于出度。
6. 对于连通有向图，所有顶点入度与出度差的绝对值之和为 2k ，则图 G 可以用 k 条路径将图 G 的每一条边经过一次，且至少要使用 k 条路径。

2.2 Hierholzier 算法

2.2.1 算法流程

任选一起点，沿任意未访问的边走到相邻节点，直至无路可走。此时必然回到起点形成了一个回路，此时图中仍有部分边未被访问。在退栈的时候找到仍有未访问边的点，从该点为起点求出另一个回路，将该回路与之前求出的回路拼接。如此反复，直至所有的边都被访问。

2.2 Fluery 算法

2.2.1 算法流程

设 $G$ 为一无向欧拉图，求 $G$ 中一条欧拉回路的算法为：

1. 任取 $G$ 中一顶点 $v0$，令 $P0=v0$;
2. 假设沿 $P_i=v_0{e}_1{v}_1{e}_2{v}_2...e_i{v}_i$ 走到顶点 $v_i$，按下面方法从 E ( G ) − { e 1 , e 2 , … , e i } E(G)-\{ e_1,e_2,…,e_i \} E(G)−{e1​,e2​,…,ei​} 中选 $ei+1$:
   1. $e_{i+1}$ 与 $v_i$ 相关联;
   2. 除非无别的边可供选择，否则$ei+1$不应该是 G i = G − { e 1 , e 2 , … , e i } G_i = G-\{ e1,e2, …,ei\} Gi​=G−{e1,e2,…,ei}中的桥。
3. 当上一项的第二步不能再进行时算法停止。可以证明的是，当算法停止时，所得到的简单回路 $P_m=v_0{e}_1{v}_1{e}_2{v}_2...e_m{v}_m,(vm=v0)$为 $G$ 中一条欧拉回路。

3. 举例说明求解过程

3.1 Hierholzier算法

我们随便取一个点，比如说 $1$ ，把它加入一个栈。
$Stac{k}_1=1]Pat{h}_1=[]$
我们用 $u$ 表示 $Stac{k}_1\to Top$
如果当前的 $u$ 点已没有未访问的出边，就将 $u$ 从 $Stac{k}_1$ 里弹出来，加入到 $Pat{h}_1$ 的前端重复上面的过程，直到 $Stac{k}_1$ 为空。
在这个过程中，
$Stac{k}_1=2]1],Pat{h}_1=[]$

$Stac{k}_1=4]2]1],Pat{h}_1=[]$

$Stac{k}_1=1]4]2]1],Pat{h}_1=[]$

$Stac{k}_1=5]4]2]1],Pat{h}_1=[1]$

$Stac{k}_1=6]5]3]2]1],Pat{h}_1=[1]$

$Stac{k}_1=4]6]5]4]2]1],Pat{h}_1=[1]$

$Stac{k}_1=2]5]4]2]1],Pat{h}_1=[6,4,1]$

$Stac{k}_1=3]2]5]4]2]1],Pat{h}_1=[6,4,1]$

$Stac{k}_1=5]3]2]5]4]2]1],Pat{h}_1=[6,4,1]$

…
所有的边都访问了，开始回溯存路径

$Stac{k}_1=],Pat{h}_1=[1,2,3,4,5,6,4,1]$

最终答案即为$Pat{h}_1$

3.2 Fluery算法

图1为连通图 $G ，现利用Fleury算法求它的欧拉通路。（注意区分：欧拉通路、欧拉回路）

其中一种欧拉通路如下：4 5 8 7 6 8 9 1 5 3 2 4 6，其搜索路径如下图所示：

现在让我们来分析算法实现过程：假设我们这样走： $4,6,8,5$ ，此时在5处有三种选择$(3,4,1)$，那么哪种能走通哪种走不通呢？答案是$(3,4)$通，$1$不通。为什么呢？来看下图：

分析：
因为$(5,1)$之间的边是除去已走过边 E ( G ) − { E 1 ( 4 , 6 ) ,   E 2 ( 6 , 8 ) ,   E 3 ( 8 , 5 ) } E(G)-\{E1(4,6),\:E2(6,8),\:E3(8,5)\} E(G)−{E1(4,6),E2(6,8),E3(8,5)}图$G$的一个桥，所谓桥即去掉该边后，剩下的所有顶点将不能够连通，即无法构成连通图。
而选择$(5,3)$和$(5,4)$则满足定义中第二条$(b)$中的要求。当然当$(5,3)$和$(5,4)$都不存在，即定义中所说“除非无别的边可供选择时”，此时就就可以选择$(5,1)$，其他情况下一定要优先选择非桥的边，否则就可能出现无法走通的情况。也就是说该搜索方法无法构成欧拉通路。如下图是选择$(5,1)$的后果：

而$(5,3)$和$(5,4)$则可以顺利完成欧拉图通路的搜索。

3.3 例题

P2731 [USACO3.3]骑马修栅栏 Riding the Fences

题目背景

Farmer John 每年有很多栅栏要修理。他总是骑着马穿过每一个栅栏并修复它破损的地方。

题目描述

John 是一个与其他农民一样懒的人。他讨厌骑马，因此从来不两次经过一个栅栏。

John 的农场上一共有 mm 个栅栏，每一个栅栏连接两个顶点，顶点用 11 到 500500 标号（虽然有的农场并没有那么多个顶点）。一个顶点上至少连接 11 个栅栏，没有上限。两顶点间可能有多个栅栏。所有栅栏都是连通的（也就是你可以从任意一个栅栏到达另外的所有栅栏）。John 能从任何一个顶点（即两个栅栏的交点）开始骑马，在任意一个顶点结束。

你需要求出输出骑马的路径（用路上依次经过的顶点号码表示)，使每个栅栏都恰好被经过一次。如果存在多组可行的解，按照如下方式进行输出：如果把输出的路径看成是一个 500500 进制的数，那么当存在多组解的情况下，输出 500500 进制表示法中最小的一个 （也就是输出第一位较小的，如果还有多组解，输出第二位较小的，以此类推）。

输入数据保证至少有一个解。

输入格式

第一行一个整数 mm，表示栅栏的数目。

从第二行到第 (m+1)(m+1) 行，每行两个整数 u,vu,v，表示有一条栅栏连接 u,vu,v 两个点。

输出格式

共 (m+1)(m+1) 行，每行一个整数，依次表示路径经过的顶点号。注意数据可能有多组解，但是只有上面题目要求的那一组解是认为正确的。

数据保证至少有一组可行解。

输入输出样例

输入

9
1 2
2 3
3 4
4 2
4 5
2 5
5 6
5 7
4 6

输出

1
2
3
4
2
5
4
6
5
7

说明/提示

对于 $100%100% $ 的数据，$1\le m\le 1024,1\le u,v\le 5001\le m\le 1024,1\le u,v\le 500$。

题目翻译来自NOCOW。

USACO Training Section 3.3

解题思路

这个题是欧拉回路的模板题，那么在这里给出一个hierholzer的做法。

对于求欧拉回路的问题，有Fluery算法和Hierholzers算法，两种算法。

后面一种算法无论是编程复杂度还是时间复杂度好像都比前种算法复杂度更优，但前者的应用广泛性好像比后者更高。

对于Hierholzers算法，前提是假设图G存在欧拉回路，即有向图任意 点的出度和入度相同。从任意一个起始点v开始遍历，直到再次到达 点v，即寻找一个环，这会保证一定可以到达点v，因为遍历到任意一 个点u，由于其出度和入度相同，故u一定存在一条出边，所以一定可 以到达v。将此环定义为C，如果环C中存在某个点x，其有出边不在环 中，则继续以此点x开始遍历寻找环C’，将环C、C’连接起来也是一个 大环，如此往复，直到图G中所有的边均已经添加到环中。

4. 算法具体步骤

4.1 Hierholzier

4.1.1 主要算法的伪代码

While s存在未被删除的无向边(s,t)
{
    delete(s,t); //删除(s,t)
    Hierholzer(t);
}
cnt += 1;
Path[cnt] = s;

5. 性能分析

时间复杂度为$O(M)$

二、哈密尔顿问题与哈密尔顿环

1859年，爱尔兰数学家哈密尔顿（Hamilton）提出下列周游世界的游戏：在正十二面体的二十个顶点上依次标记伦敦、巴黎、莫斯科等世界著名大城市，正十二面体的棱表示连接这些城市的路线。试问能否在图中做一次旅行，从顶点到顶点，沿着边行走，经过每个城市恰好一次之后再回到出发点。

1. 问题概述

哥尼斯堡七桥问题是在寻找一条遍历图中所有边的简单路径，而哈密尔顿的周游世界问题则是在寻找一条遍历图中所有点的基本路径。在无向图G=<V,E>中，遍历G中每个顶点一次且仅一次的路径称为哈密尔顿路径（Hamiltonian path），遍历G中每个顶点一次且仅一次的回路称为哈密尔顿回路（Hamiltonian cycle）。具有哈密尔顿回路的图称为哈密尔顿图（英语：Hamiltonian graph，或Traceable graph）。

2. 求解算法思想

2.1 必要条件与充分条件

1. 必要非充分条件：对V的每个非空真子集 $S$ 均有 $w(G-S)<=|S|$ ，其中$|S|$是$S$中的顶点数， $w(G-S)$表示$G$删去顶点集$S$后得到的图的连通分图个数。
2. 充分非必要条件：如果图 $G=<V,E>$ 是具有$n\ge 3$个顶点的简单无向图，且在图$G$中每一对顶点的度数和都不小于$n$ ，那么 $G$ 中必然存在一条哈密尔顿回路。

2.2 P与NP问题

1. P问题：
   在计算理论中，我们定义P类是确定形 单带图灵机在多项式时间内 可以判定的 语言类，即 $$\prod _{k}TIME(n^k)$$P大致对应于在计算机上实际可以解的问题类。
2. NP问题：
   与之相对应的，还有$NP$类，$NP$类是具有多项式时间验证机的语言类，其中验证机的定义如下：语言A的验证机是一个算法$V$，其中 A = { w ∣ 对 某 个 字 符 串 c , V 接 受 < w , c > } A = \{w | 对某个字符串c, V 接受<w,c>\} A={w∣对某个字符串c,V接受<w,c>}
3. 多项式时间可验证性：
   因为只根据w的长度来度量验证机的时间 ，所以多项式时间验证机在w的长度的多项式时间内运行。如果语言$A$有一个多项式时间验证机，我们就称它是多项式时间可验证的。
4. 成员与成员资格证书：
   验证机利用额外的信息（即上述定义中的符号 $c$ ）来验证字符串 $w$ 是 $A$ 的成员。该信息称为 $A$ 的成员资格证书．或证明。注意，对于多项式验证机，证书具有多项式的长度（ $w$ 的长度），因为这是该验证机在它的时间界限内所能访问的全部信息长度。
5. $NP$ 的意思就是非确定型多项式时间，这也是使用非确定型多项式时间图灵机的一个特征。一个非常重要的定理就是：一个语言在 $NP$ 中，当且仅当它能被某个非确定型多项式时间图灵机判定。

2.1.3 判定方法

2.1.3.1 基本必要条件

设图$G=<V,E>$是哈密顿图,则对于$v$的任意一个非空子集$S$,若以$|S|$表示$S$中元素的数目,$G-S$表示$G$中删除了S中的点以及这些点所关联的边后得到的子图,则$W(G-S)\le |S|$成立.其中$W(G-S)$是$G-S$中联通分支数。

2.1.3.2 Dirac定理(充分条件)

设一个无向图中有N个顶点,若所有顶点的度数大于等于N/2,则哈密顿回路一定存在.(N/2指的是⌈N/2⌉,向上取整)

2.1.3.3 竞赛图(哈密顿通路)

N(N>=2)阶竞赛图一点存在哈密顿通路.

3. 举例说明求解过程

3.1 在Dirac定理的前提下构造哈密顿回路

3.1.1 过程

1. 任意找两个相邻的节点 $S$ 和 $T$ ,在其基础上扩展出一条尽量长的没有重复结点的路径.即如果 $S$ 与结点 $v$ 相邻,而且 $v$ 不在路径$S\to T$ 上,则可以把该路径变成 $v\to S\to T$ ,然后 $v$ 成为新的 $S$ .从 $S$ 和 $T$ 分别向两头扩展,直到无法继续扩展为止,即所有与 $S$ 或 $T$ 相邻的节点都在路径 $S\to T$ 上.
2. 若S与T相邻,则路径 $S\to T$ 形成了一个回路.
3. 若S与T不相邻,可以构造出来一个回路.设路径 $S\to T$ 上有 $k+2$ 个节点,依次为 $S,v_1,v_2,...,v_k,T$ .可以证明存在节点 $v_i(i\in [1,k])$ ,满足 $vi$ 与 $T$ 相邻,且 $v_{i+1}$ 与 $S$ 相邻.找到这个节点 $v_i$ ,把原路径变成 $S\to vi\to T\to v_{i+1}$ ,即形成了一个回路.
4. 到此为止,已经构造出来了一个没有重复节点的的回路,如果其长度为 $N$ ,则哈密顿回路就找到了.如果回路的长度小于 $N$ ,由于整个图是连通的,所以在该回路上,一定存在一点与回路之外的点相邻.那么从该点处把回路断开,就变回了一条路径,同时还可以将与之相邻的点加入路径.再按照步骤1的方法尽量扩展路径,则一定有新的节点被加进来.接着回到路径2.

3.2 N(N>=2)阶竞赛图构造哈密顿通路

3.2.1 过程

设当 $n=k+1$ 时,第 $k+1$ 个节点为 $V_{k+1}$ ,考虑到 $V_{k+1}$ 与 $V_i(1\le i\le k)$ 的连通情况,可以分为以下两种情况.

1. $V_k$与 $V_{k+1}$ 两点之间的弧为 $<V_k,V_{k+1}>$ ,则可构造哈密顿路径 $V_1,V_2,...,V_k,V_{k+1}$ .
2. $V_k$ 与 $V_{k+1}$ 两点之间的弧为 $<V_{k+1},V_k>$ ,则从后往前寻找第一个出现的 $V_i(i=k-1,i\ge 1,)$ ,满足 $Vi$ 与 $V_{k+1}$ 之间的弧为 $<V_i,V_{k+1}>$ ,则构造哈密顿路径 $V_1,V_2,...,V_i,V_{k+1},V_{i+1},....,V_k$ .若没找到满足条件的 $V_i$ ,则说明对于所有的 $V_i(1\le i\le k)$ 到 $V_{k+1}$ 的弧为 $<V_{k+1},V_i>$ ,则构造哈密顿路径 $V_{k+1},V_1,V_2,...,V_k$ .

3.2.2 用图来说明

假设此时已经存在路径$V_1\to V_2\to V_3\to V_4$ ,这四个点与 $V_5$ 的连通情况有16种,给定由0/1组成的四个数,第$i$个数为0代表存在弧 $<V_5,V_i>$ ,反之为1,表示存在弧 $<V_i,V_5>$

$sign[]= { 0, 0, 0, 0 } $.很显然属于第二种情况,从后往前寻找不到1,即且不存在弧$<V_i, V_5>$ .则构造哈密顿路:$V_5\to V_1\to V_2\to V_3\to V_4$.

$sign[]= { 0, 0, 0, 1 } $.
属于第一种情况,最后一个数字为1,即代表存在弧 $<V_i,V_5>$ 且 $i=4$ (最后一个点)则构造哈密顿路: $V_1\to V_2\to V_3\to V_4\to V_5$.

$sign[]= { 0, 0, 1, 0 } $.属于第二种情况,从后往前找到1出现的第一个位置为3.构造哈密顿路:$V_1 \rightarrow V_2 \rightarrow V_3 \rightarrow V_5 \rightarrow V_4$.

$sign[]= { 0, 0, 1, 1 } $.
属于第一种情况,最后一个数字为1,即代表存在弧 $<V_i,V_5>$ 且 $i=4$ (最后一个点)则构造哈密顿路:$V_1 \rightarrow V_2 \rightarrow V_3\rightarrow V_4 \rightarrow V_5 $.

$sign[]= { 0, 1, 0, 0 } $.属于第二种情况,从后往前找到1出现的第一个位置为2.构造哈密顿路:$V_1 \rightarrow V_2 \rightarrow V_5 \rightarrow V_3\rightarrow V_4$.

$sign[]= { 0, 1, 0, 1 } $.属于第一种情况,最后一个数字为1,即代表存在弧$<V_i, V_5>$且$i=4$(最后一个点)则构造哈密顿路:$V_1 \rightarrow V_2 \rightarrow V_3 \rightarrow V_4 \rightarrow V_5$.

$sign[]= { 1, 0, 1, 0 } $.属于第二种情况,从后往前找到1出现的第一个位置为3.构造哈密顿路:$V_1 \rightarrow V_2 \rightarrow V_3 \rightarrow V_5 \rightarrow V_4$.

$sign[]= { 1, 1, 1, 0 } $.属于第二种情况,从后往前找到1出现的第一个位置为3.构造哈密顿路:$V_1 \rightarrow V_2 \rightarrow V_3 \rightarrow V_5 \rightarrow V_4$.

4. 算法具体步骤

void Hamilton(int ans[maxN + 7], bool map[maxN + 7][maxN + 7], int n){
    Init();
    bool visit[maxN + 7] = {false};
    for(i = 1; i <= n; i++) if(map[s][i]) break;
    t = i;//取任意邻接与s的点为t
    visit[s] = visit[t] = true;
    ans[0] = s;
    ans[1] = t;
    while(true){
        while(true){//从t向外扩展
            for(i = 1; i <= n; i++){
                if(map[t][i] && !visit[i]){
                    ans[ansi++] = i;
                    visit[i] = true;
                    t = i;
                    break;
                }
            }
            if(i > n) break;
        }
        //将当前得到的序列倒置,s和t互换,从t继续扩展,相当于在原来的序列上从s向外扩展
        Hreverse(ansi, ans, i, w)
        temp = s;
        s = t;
        t = temp;
        while(true){//从新的t继续向外扩展,相当于在原来的序列上从s向外扩展
            for(i = 1; i <= n; i++){
                if(map[t][i] && !visit[i]){
                    ans[ansi++] = i;
                    visit[i] = true;
                    t = i;
                    break;
                }
            }
            if(i > n) break;    
        }
        if(!map[s][t]){//如果s和t不相邻,进行调整
            for(i = 1; i < ansi - 2; i++)//取序列中的一点i,使得ans[i]与t相连,并且ans[i+1]与s相连
                if(map[ans[i]][t] && map[s][ans[i + 1]])break;
            w = ansi - 1;
            i++;
            t = ans[i];
            reverse(ans, i, w);//将从ans[i +１]到ｔ部分的ans[]倒置
        }//此时s和t相连
        if(ansi == n) return;//如果当前序列包含n个元素,算法结束
        for(j = 1; j <= n; j++){//当前序列中元素的个数小于n,寻找点ans[i],使得ans[i]与ans[]外的一个点相连
            if(visit[j]) continue;
            for(i = 1; i < ansi - 2; i++)if(map[ans[i]][j])break;
                if(map[ans[i]][j]) break;
        }
        s = ans[i - 1];
        t = j;//将新找到的点j赋给t
        reverse(ans, 0, i - 1);//将ans[]中s到ans[i-1]的部分倒置
        reverse(ans, i, ansi - 1);//将ans[]中ans[i]到t的部分倒置
        ans[ansi++] = j;//将点j加入到ans[]尾部
        visit[j] = true;
    }

5. 性能分析

时间复杂度

1. Dirac定理：如果说每次到步骤5算一轮的话,那么由于每一轮当中至少有一个节点被加入到路径 $S\to T$ 中,所以总的轮数肯定不超过n轮,所以时间复杂度为 $O(n^2)$ .空间上由于边数非常多,所以采用邻接矩阵来存储比较适合

三、中国邮递员问题

著名图论问题之一。邮递员从邮局出发送信，要求对辖区内每条街，都至少通过一次，再回邮局。在此条件下，怎样选择一条最短路线？此问题由中国数学家管梅谷于1960年首先研究并给出算法，故名。中国邮递员问题——可以叙述为在一个有奇点的图中，通过增加一些重复边，使新图不含奇点，并且重复边的总权为最小问题！

1. 问题概述

中国邮递员问题是邮递员在某一地区的信件投递路程问题。邮递员每天从邮局出发，走遍该地区所有街道再返回邮局，问题是他应如何安排送信的路线可以使所走的总路程最短。这个问题由中国学者管梅谷在1960年首先提出，并给出了解法——“奇偶点图上作业法”，被国际上统称为“中国邮递员问题”。用图论的语言描述，给定一个连通图G，每边e有非负权)，要求一条回路经过每条边至少一次，且满足总权最小。
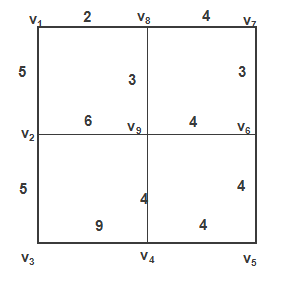
快递员从V1出发给V2、V3、V4、V5、
V6、V7、V8、V9派发快递，求派完所有回到原出发点的最短路径？如下图所示

2. 求解算法思想

1. 建立街区无向网的邻接矩阵;
2. 求各顶点的度数;
3. 求出所有奇度点;
4. 求出每一个奇度点到其它奇度点的最短路径;
5. 找出距离最短的添加方案;
6. 根据最佳方案添加边，对图进行修改，使之满足一笔画的条件;
7. 对图进行一笔画，并输出;

3. 举例说明求解过程

如上图举例

3.1 题目分析

在分析这道题目之前，我们在想这样的一个问题
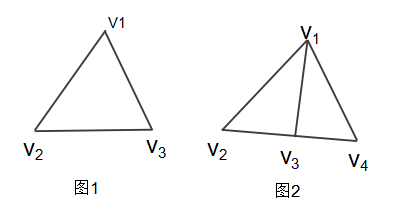
图1和图2当中哪一个图满足从
图中任何一点出发，途径每条边最终还能回到原点？
图1无奇点不需要走重复边；
图2有奇点需要走重复边。

3.2 过程

满足各个结点的度为偶数！在一个多重边的连通图中，从某个顶点出发，经过不同的线路，又回到原出发点，这样的线路必是欧拉图。

定理1：连通的多重图G是欧拉图，当且仅当G中无奇点。

欧拉圈：若存在一个简单圈，过每边一次，且仅一次，则称为欧拉圈。

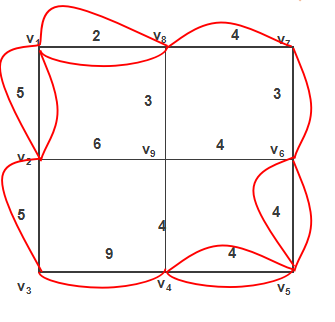
1. 化奇图为偶图，结果如下：
   

   注意：不是将跨越的奇点连接起来！

2. 但是上面这样的连接结果是最优方案？如果不是最优方案，那么什么样的指标才算是最优的方案？应该如果去找到这样的最优方案？最后对化奇图为偶图进行下面两个约束条件调优：

   1. 在最优方案中，图的每一边最多有一条重复边
   2. 最优方案中，图中的每一个圈（环）重复边的总权值不大于该圈总权值的一半

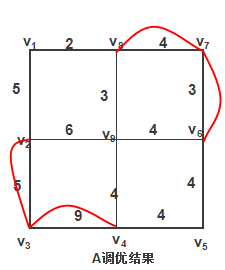
   下面图是经过1约束条件的调优结果：
   

   约束条件调优算法执行的步骤：

   1. 找出图中的一个圈，既一条不存在重复路径的回路
   2. 计算圈中的重复边的总和D，计算圈的所有边的总和S
   3. 如果$D>\frac{S}{2}$，则把这个圈的重复边全部变成单边，单边全部变成重复边
   4. 重复以上的$1,2,3$直到不存在$D>\frac{S}{2}$的情况

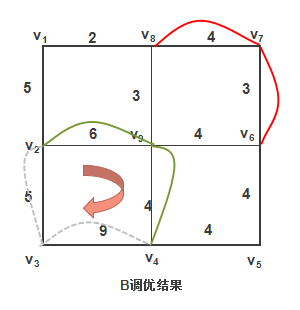
   最优在A的调优结果基础上面，B调优结果如下：
   

3. 圈$(v_2,v_3,v_4,v_9,v_2)$ 的总长度为24，但圈上重复边总权为14，大于该圈总长度的一半，因此可以做一次调整，以 $[v_2,v_9]$, $[v_9,v_4]$ 上的重复边代 $[v_2,v_3]$, $[v_3,v_4]$ 上的重复边，使重复边总长度下降为17。

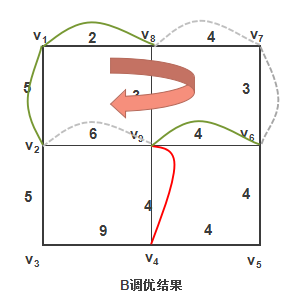
4. 但是上面的图还存在可以调优的情况：
   圈$(v1,v2,v9,v6,v7,v8,v1)$ 的总长度为24，但圈上重复边总权为13，大于该圈总长度的一半，因此可以做一次调整，使重复边总长度下降为15。结果如下图:
   

4. 算法具体步骤

void Chinaemailman(){
    //化奇图为偶图
    transOddToEven(G, n, m);
    //图的每一边最多有一条重复边
    for (int i = 0; i < G.n(); i++)
    {
        for (int j = 0; j < G.node[i].size(); j++)
        {
            if (isEdge(i, j))
            {
                if (i > j)
                {
                    G.nreverse(i, j);
                }
            }
        }
        sort(G.node.begin(), G.node.end(), cmp);
        G.node.del();
    }
    //图中的每一个圈（环）重复边的总权值不大于该圈总权值的一半
    while (true)
    {
        Graph g = G.findCircle();//找出图中的一个圈，既一条不存在重复路径的回路
        if (g._null())
        {
            break;  
        }
        //计算圈中的重复边的总和D，计算圈的所有边的总和S
        int D = 0, S = 0;
        for (int i = 0; i < g.e(); i++)
        {
            if (G.edgeDouble(i))
            {
                D += G.getEdgeW(i);
            }
            s += G.getEdgeW(i);
        }
        //如果D>S/2，则把这个圈的重复边全部变成单边，单边全部变成重复边
        if (D > S / 2)
        {
            G.gotoagainst
        }
        else
        {//重复以上的1,2,3直到不存在D > S/2的情况
            break;
        }
    }

}

5. 性能分析

时间复杂度

根据算法有 $O(N^2)$ 和 $O(N^3)$，上述算法为 $O(N^2)$.

四、旅行推销员问题

一名推销员要拜访多个地点时，如何找到在拜访每个地点一次后再回到起点的最短路径。规则虽然简单，但在地点数目增多后求解却极为复杂。

1. 问题概述

旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

2. 求解算法思想

2.1 动态规划法

2.1.1 算法描述

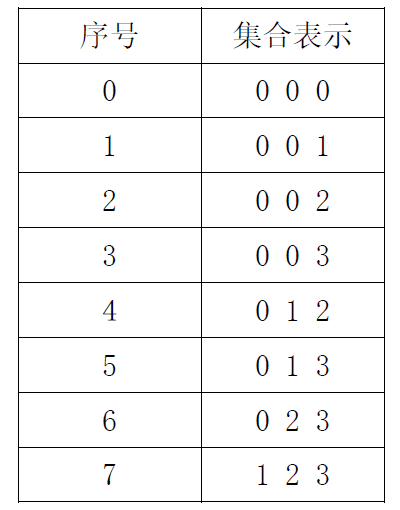
1. 假定我们从城市1出发，经过了一些地方，并到达了城市j。毋庸置疑，我们需要记录的信息有当前的城市j。同时我们还需要记录已经走过的城市的集合。同理，使用S记录未走过的城市的集合也可以的，且运算方便。
2. 于是我们可以得出状态转移方程 g o ( S , i n i t ) = m i n { g o ( S − i , i ) + d p [ i ] [ i n i t ] } ∀ s ∈ S g o ( s , i n i t ) go(S,init)=min \{ go(S−i,i)+dp[i][init] \} ∀s∈S go(s,init) go(S,init)=min{go(S−i,i)+dp[i][init]}∀s∈Sgo(s,init)表示从init点开始，要经过s集合中的所有点的距离
3. 因为是NP问题，所以时间复杂度通常比较大。使用dis[s][init]用来去重，初始化为-1，如果已经计算过init—>S（递归形式），则直接返回即可

2.1.2 数学描述及函数

设从顶点i出发，令 $d(i,V^{\prime })$ 表示从顶点i出发经过 $V^{\prime }$ 中各个顶点一次且仅一次，最后回到出发点 $i$ 的最短路径长度，开始时， $V’＝V - { i } $，于是，TSP问题的动态规划函数为：$ d ( i , V ′ ) = m i n { c i k + d ( k , V − { k } ) } ( k ∈ V ′ ) d(i, V') = min \{ cik + d(k, V - \{ k \}) \} (k∈V') d(i,V′)=min{cik+d(k,V−{k})}(k∈V′)$ d ( k , { } ) = c k i ( k ≠ i ) d(k,\{ \}) = cki(k ≠ i) d(k,{})=cki(k​=i)

2.2 分支界限法

2.2.1 算法介绍

1. 解旅行售货员问题的优先队列式分支限界法用优先队列存储活结点表。
2. 活结点m在优先队列中的优先级定义为：活结点m对应的子树费用下界lcost。
3. lcost=cc+rcost，其中，cc为当前结点费用，rcost为当前顶点最小出边费用加上剩余所有顶点的最小出边费用和。
4. 优先队列中优先级最大的活结点成为下一个扩展结点。
5. 排列树中叶结点所相应的载重量与其优先级（下界值）相同，即：叶结点所相应的回路的费用(bestc)等于子树费用下界lcost的值。
6. 与子集树的讨论相似，实现对排列树搜索的优先队列式分支限界法也可以有两种不同的实现方式：(旅行售货员问题采用第一种实现方式。)

2.2.2 算法描述

1. 要找最小费用旅行售货员回路，选用最小堆表示活结点优先队列。
2. 算法开始时创建一个最小堆，用于表示活结点优先队列。
3. 堆中每个结点的优先级是子树费用的下界lcost值。
4. 计算每个顶点i的最小出边费用并用minout[i]记录
5. 如果所给的有向图中某个顶点没有出边，则该图不可能有回路，算法结束。

3. 举例说明求解过程

3.1 动态规划法

如图

3.2 分支限界法

如图

4. 算法具体步骤

4.1 动态规划法

for (i=1; i<n; i++)     //初始化第0列
	d[i][0]=c[i][0]; 
 for (j=1; j<2n-1-1; j++)  
 	for (i=1; i<n; i++)   //依次进行第i次迭代
		if (子集V[j]中不包含i) 
 			对V[j]中的每个元素k，计算[i][j]=min(c[i][k]+d[k][j-1]);
对V[2n-1-1]中的每一个元素k，计算d[0][2n-1-1]=min(c[0][k]+d[k][2n-1-2]);
输出最短路径长度d[0][2n-1-1];

4.2 分支限界法

void Travel_Backtrack(int t){
    int i,j;
    if(t>N){                         //走完了，输出结果
        for(i=1;i<=N;i++)            //输出当前的路径
            cout<<x[i];
        cout<<endl;
        if(cw < bestw){              //判断当前路径是否是更优解
            for (i=1;i<=N;i++){
                bestx[i] = x[i];
            }
            bestw = cw+City_Graph[x[N]][1];
        }
        return;
    }
    else{
        for(j=1;j<=N;j++){           //找到第t步能走的城市
            if(City_Graph[x[t-1]][j] != NO_PATH && !isIn[j]){ //能到而且没有加入到路径中
                isIn[j] = 1;
                x[t] = j;
                cw += City_Graph[x[t-1]][j];
                Travel_Backtrack(t+1);
                isIn[j] = 0;
                x[t] = 0;
                cw -= City_Graph[x[t-1]][j];
            }
        }
    }
}

5. 性能分析

1. 动态规划法的时间复杂度为$O(N^2)$
2. 分支限界法的时间复杂度为$O(N^2)$
   
   
   
   

参考资料

• [1]Handwer.干货｜欧拉图学习笔记 - 知乎[J/OL]
• [2]青君.欧拉回路与欧拉路径总结[J/OL]
• [3]guomutian911.Fleury (弗罗莱) 算法通俗解释[J/OL]
• [4]USACO3.3.P2731 [USACO3.3]骑马修栅栏 Riding the Fences[J/OL]
• [5]Misaka_Azusa.题解 P2731 【骑马修栅栏 Riding the Fences】[J/OL]
• [6]白马负金羁.从哈密尔顿路径谈NP问题[J/OL]
• [7]itaoer.哈密尔顿回路_百度百科[J/OL]
• [8]肘子zhouzi.[哈密顿图 哈密顿回路 哈密顿通路(Hamilton)]https://blog.csdn.net/zhouzi2018/article/details/81278942()[J/OL]
• [9]老司机的诗和远方.ACM图论算法—邮递员投递问题[J/OL]
• [10]아름다운 밤.中国邮路算法（中国邮递员问题）（详细）[J/OL]
• [11]孙和军.旅行推销员问题_百度百科[J/OL]
• [12]张连明.旅行商问题_百度百科[J/OL]
• [13]与世无争的小正太.动态规划经典问题–TSP问题[J/OL]
• [14]小莫の咕哒君.旅行售货员问题-分支限界法(优先队列式分支限界法)[J/OL]
• [15]VM_Alike.TSP问题，动态规划法[J/OL]
• [16]关关雎鸠儿.【分支限界法】求解TSP问题[J/OL]
  AE%E9%A2%98/840008?fromtitle=%E6%97%85%E8%A1%8C%E6%8E%A8%E9%94%80%E5%91%98%E9%97%AE%E9%A2%98&fromid=10675002&fr=aladdin)[J/OL]
• [12]张连明.旅行商问题_百度百科[J/OL]
• [13]与世无争的小正太.动态规划经典问题–TSP问题[J/OL]
• [14]小莫の咕哒君.旅行售货员问题-分支限界法(优先队列式分支限界法)[J/OL]
• [15]VM_Alike.TSP问题，动态规划法[J/OL]
• [16]关关雎鸠儿.【分支限界法】求解TSP问题[J/OL]