Educoder 头歌【人工智能之决策树算法】

第1关：决策树算法求解分类预测问题

任务描述

本关任务：学习决策树，并基于离散的输入值和输出值数据归纳实现样例的布尔分类。

现有一些是否决定在该饭店等待餐桌吃饭的数据(x,y)，其中x是输入属性的值向量，y是单一布尔输出值，学员需要分析数据，构造一棵决策树，学习目标谓词 WillWait 的预测（ Yes 或者 No ），每一条数据属性如下：

• Alternate ：附件是否有一个更合适的候选饭店（Yes 和 No）；

• Bar ：饭店中是否有舒适的酒吧等待区（Yes 和 No）；

• Fri/Sat ：当今天是星期五或星期六时，该属性为真 Yes ，否则为假 No；

• Hungry ：是否饿了（Yes 和 No）；

• Patrons ：饭店中有多少客人，取值为 None 、 Some 和 Full；

• Price ：饭店价格区间；

• Raining ：是否下雨（Yes 和 No）；

• Reservation ：是否预定（Yes 和 No）；

• Type ：饭店类型（French 、 Italian 、 Thai 和 Burger）；

• WaitEstimate ：对等待时间的估计（010 、 1030 、 30~60 和 >60 分钟）。

相关知识

为了完成本关任务，你需要掌握：1.决策树，2. ID3 算法，3.求解思路。

决策树

决策树表示一个函数，以属性值向量作为输入，返回一个“决策”，对于输入值是离散的和输出值是二值的情况，通常将这称之为布尔分类，其中样例输入被分类为正例（真）或反例（假），决策树在过程中则是通过一系列的计算测试达到决策的目的。

决策树学习的搜索策略是贪婪搜索策略，近似于极小化搜索树的深度，主要思想就是挑选分叉的属性，以便于尽可能对样例进行正确分类。一个完美属性可以将样例全部划分为正例集合和反例集合，这些集合对应决策树的叶子结点，哪些属性优先被选择就是决策树算法的核心，常见的选择算法有 ID3 算法和 C4.5 算法，本关卡重点介绍和学习 ID3 算法。

ID3算法

ID3（Iterative Dichotomiser 3 迭代二叉树三代） 算法是由 Ross Quinlan 发明的，它建立在奥卡姆剃刀理论的基础上，即越是小型的决策树越是优于大型的决策树，实际上也是一个启发式算法，是一种自顶向下增长树的贪婪算法，在每个结点选取能最好地分类样例的属性，重复这个过程，直到这棵树能完美分类训练样本或所有的属性都使用过了，其算法伪代码如下：
奥卡姆剃刀理论阐述了一个信息熵的概念，以此来选择最优分类属性。设随机变量$V$具有值$v_k$，各自的概率表示为$P(v_k)$，则$V$的熵的定义为：举个例子来理解信息熵的定义，随机抛掷一枚硬币，出现正面和反面的概率都为0.5，根据以上熵的定义，可以得出以下式子：
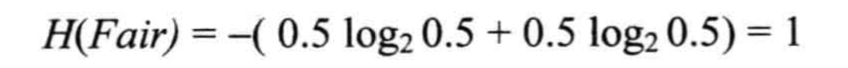借助这个例子，设布尔随机变量以$q$的概率为真，则可定义该变量的熵为：

那么对于拥有多个属性的数据来说，ID3选择属性的方式则是计算该属性的信息增益（收益），信息增益最大的被优先选择作为决策树的分支属性。

带有$d$个不同值的属性$A$将训练集$E$划分为$E_1,...,E_d$，每个子集$E^{}$