数字信号处理_使用MATLAB研究零点分布对于单位脉冲响应的影响

下面四个二阶网络的系统函数具有相同的极点分布：

使用MATLAB研究零点分布对于单位脉冲响应的影响：
①分别画出各系统的零极点分布图；
②分别求出各系统的单位脉冲响应，并画出其波形；
③分析零点分布对于单位脉冲响应的影响。

A=[1,-1.6,0.9425];  %分母多项式，都是相同的
%四个分子多项式
B1=1;
B2=[1,-0.3];
B3=[1,-0.8];
B4=[1,-1.6,0.8];
b1=[1,0,0];
b2=[1,-0.3,0];
b3=[1,-0.8,0];
b4=[1,-1.6,0.8];
p=roots(A)  %求极点
%%%求零点
z1=roots(b1)
z2=roots(b2)
z3=roots(b3)
z4=roots(b4)
%%%计算单位脉冲响应的100个样值
[h1n,n]=impz(B1,A,100);
[h2n,n]=impz(B2,A,100);
[h3n,n]=impz(B3,A,100);
[h4n,n]=impz(B4,A,100);
figure(1)
zplane(B1,A);   %绘制H1的零极点图
figure(2)
stem(n,h1n,'.');    %绘制h1的波形图
line([0,100],[0,0])
xlabel('n');ylabel('h1(n)');
figure(3)
zplane(B2,A);   %绘制H2的零极点图
figure(4)
stem(n,h2n,'.');    %绘制h2的波形图
line([0,100],[0,0])
xlabel('n');ylabel('h2(n)');
figure(5)
zplane(B3,A);   %绘制H3的零极点图
figure(6)
stem(n,h3n,'.');    %绘制h3的波形图
line([0,100],[0,0])
xlabel('n');ylabel('h3(n)');
figure(7)
zplane(B4,A);   %绘制H4的零极点图
figure(8)
stem(n,h4n,'.');    %绘制h4的波形图
line([0,100],[0,0])
xlabel('n');ylabel('h4(n)');

四种系统函数的极点分布一样，只是零点不同。
第一种零点在原点，不影响系统的频率响应，也不影响单位脉冲响应。

第二种的零点在实轴上，但离极点较远。

第三种的零点靠近极点。

第四种的零点非常靠近极点。

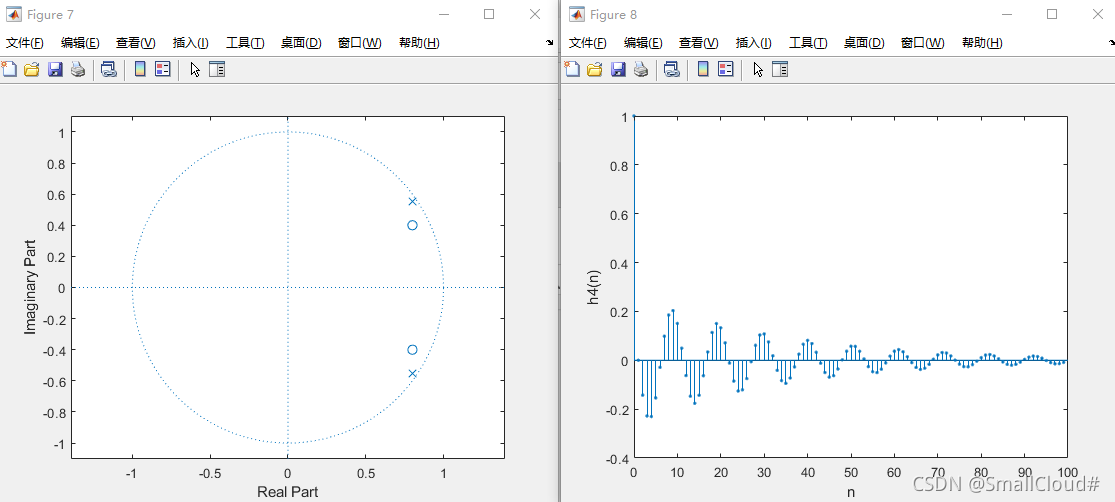
可以发现零点越靠近极点，单位脉冲响应的变化越缓慢，因此零点对极点的作用起抵消作用。（第四种有两个零点，抵消作用更明显）

---

零点分布对单位脉冲响应的影响取决于零点的位置以及数量。

如果零点分布在低频区域，则单位脉冲响应会有较长的持续时间，并且对低频信号的抑制能力较强。相反，如果零点分布在高频区域，则单位脉冲响应的持续时间会缩短，并且对高频信号的抑制能力较弱。

此外，零点的数量也会影响单位脉冲响应的形态。通常，零点越多，单位脉冲响应就越平稳，抑制能力也越强。因此，设计数字滤波器时，需要考虑零点分布的影响，以获得所需的滤波器性能。