两种经典的去噪算法NLM和BM3D

钟屿

已于 2024-12-16 11:42:18 修改

阅读量741

点赞数 5

文章标签：算法人工智能计算机视觉图像处理

于 2024-12-13 20:31:20 首次发布

本文链接：https://blog.csdn.net/qq_45987837/article/details/144459172

版权

噪声模型

图像中噪声的来源有许多种，这些噪声来源于图像采集、传输、压缩等各个方面。噪声的种类也各不相同，比如椒盐噪声，高斯噪声等，针对不同的噪声有不同的处理算法。

对于输入的带有噪声的图像v(x)，其加性噪声可以用一个方程来表示： $\eta (x),\quad x \in \Omega ,$

其中 $u (x)$ 是原来没有噪声的图像。 $x$ 是像素集合， $\eta (x)$ 是加项噪声项，代表噪声带来的影响。 $\Omega$ 是像素的集合，也就是整幅图像。从这个公式可以看出，噪声是直接叠加在原始图像上的，这个噪声可以是椒盐噪声、高斯噪声。理论上来说，如果能够精确地获得噪声，用输入图像减去噪声就可以恢复出原始图像。但现实往往很骨感，除非明确地知道噪声生成的方式，否则噪声很难单独求出来。

工程上，图像中的噪声常常用高斯噪声 ${\rm N}(\mu ,{\sigma ^2})$ 来近似表示，其中 $\mu = 0$ ， ${\sigma ^2}$ 是噪声的方差， ${\sigma ^2}$ 越大，噪声越大。一个有效的去除高斯噪声的方式是图像求平均，对N幅相同的图像求平均的结果将使得高斯噪声的方差降低到原来的N分之一，现在效果比较好的去噪算法都是基于这一思想来进行算法设计。

NL-Means算法

NL-Means的全称是：Non-Local Means，直译过来是非局部平均，在2005年由Baudes提出，该算法使用自然图像中普遍存在的冗余信息来去噪声。与常用的双线性滤波、中值滤波等利用图像局部信息来滤波不同的是，它利用了整幅图像来进行去噪，以图像块为单位在图像中寻找相似区域，再对这些区域求平均，能够比较好地去掉图像中存在的高斯噪声。
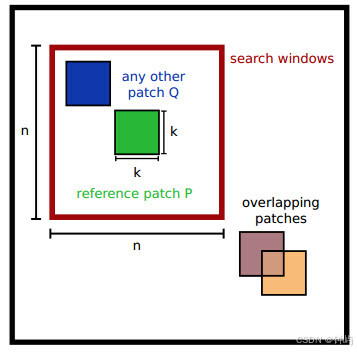
非局部均值充分利用了图像中的冗余信息，在去噪的同时能最大程度地保持图像的细节特征。他的基本思想是当前像素的估计值由图像中与它具有相似邻域结构的像素加权平均得到。在理论上，该算法需要在整个图像范围内判断像素间的相似度，也就是说，每处理一个像素点时，都要计算它与图像中所有像素点间的相似度。但实际上，考虑到效率问题，实现的时候，会设定两个固定大小的窗口，搜索窗口和邻域窗口。邻域窗口在搜索窗口中滑动，根据邻域间的相似性确定像素的权值。
NL-Means的滤波过程可以用下面公式来表示： $\tilde u(x) = \sum\limits_{y \in {\Omega _x}} {w(x,y)v(y)}.$

在这个公式中， $w (x, y)$ 是一个权重，表示在原始图像 $v$ 中，像素 $x$ 和像素 $y$ 的相似度。这个权重要大于0，同时，权重的和为1，用公式表示是这样： $0\quad and\quad \sum\limits_{y \in {\Omega _x}} {w(x,y) = 1}, \quad \forall x \in \Omega ,y \in {\Omega _x} .$

$\Omega _x$ 是像素 $x$ 的邻域。这个公式可以这样理解：对于图像中的每一个像素 $x$ ，去噪之后的结果等于它邻域中像素 $y$ 的加权和，加权的权重等于 $x$ 和 $y$ 的相似度。 这个邻域也称为搜索区域，搜索区域越大，找到相似像素的机会也越大，但同时计算量也是成指数上升。在提出这个算法的文献中，这个区域是整幅图像！导致的结果是处理一幅512x512大小的图像，最少也得几分钟。

衡量像素相似度的方法有很多，最常用的是根据两个像素的亮度值的差的平方来估计。但因为有噪声的存在，单独的一个像素并不可靠。对此解决方法是，考虑它们的邻域，只有邻域相似度高才能说这两个像素的相似度高。衡量两个图像块的相似度最常用的方法是计算他们之间的欧氏距离： $\over {n(x)}}\exp ({{\left\| {{\bf{V}}(x) - {\bf{V}}(y)} \right\|_{2,a}^2} \over {{h^2}}}).$

其中： $n (x)$ 是一个归一化的因子，是所有权重的和，对每个权重除以该因子后，使得权重满足和为1的条件。 $h > 0$ 是滤波系数，控制指数函数的衰减从而改变欧氏距离的权重。 ${\bf{V}}(x)$ 和 ${\bf{V}}(y)$ 代表了像素 $x$ 和像素 $y$ 的邻域，这个邻域常称为块(Patch)邻域。块邻域一般要小于搜索区域。 ${\left\| {{\bf{V}}(x) - {\bf{V}}(y)} \right\|_{2,a}^2}$ 是两个邻域的高斯加权欧式距离。其中 $a > 0$ 是高斯核的标准差。在求欧式距离的时候，不同位置的像素的权重是不一样的，距离块的中心越近，权重越大，距离中心越远，权重越小，权重服从高斯分布。实际计算中考虑到计算量的问题，常常采用均匀分布的权重。
讲了这么多，是时候用图来说明问题了：
请添加图片描述
如上图所示，p为去噪的点，因为q1和q2的邻域与p相似，所以权重 $w (p, q 1)$ 和 $w (p, q 2)$ 比较大，而邻域相差比较大的点q3的权重值 $w (p, q 3)$ 很小。如果用一幅图把所有点的权重表示出来，那就得到下面这些权重图：

请添加图片描述
上面这6组图像是我们所举的六个例子。每个例子的左边是原图，中心的白色色块代表了像素 $x$ 邻域窗口，右边是计算出来的权重 $w (x, y)$ 图，权重范围从0（黑色）到1（白色）。这个邻域在整幅图像中移动，计算图像中其他区域跟这个块的相似度，相似度越高，得到的权重越大。最后将这些相似的像素值根据归一化之后的权重加权求和，得到的就是去噪之后的图像了。

这个算法参数的选择也有讲究，一般而言，考虑到算法复杂度，搜索区域大概取21x21，相似度比较的块的可以取7x7。实际中，常常需要根据噪声来选取合适的参数。当高斯噪声的标准差 $\sigma$ 越大时，为了使算法鲁棒性更好，需要增大块区域，块区域增加同样也需要增加搜索区域。同时，滤波系数 $h$ 与 $\sigma$ 正相关： $h=k\sigma$ ，当块变大时， $k$ 需要适当减小。

NL-Means算法的复杂度跟图像的大小、颜色通道数、相似块的大小和搜索框的大小密切相关，设图像的大小为N $\times$ N，颜色通道数为 $N_c$ ，块的大小为k $\times$ k，搜索框的大小为n $\times$ n，那么算法复杂度为： $O({N^2}{N_c}{k^2}{n^2})$ 。对512 $\times$ 512的彩色图像而言，设置k=7，n=21，OpenCV在使用了多线程的情况下，处理一幅图像所需要的时间需要几十秒。虽然有人不断基于这个算法进行改进、提速，但离实时处理还是比较远。

最后来看一下这个算法的去噪效果：

请添加图片描述

BM3D算法

BM3D（Block-matching and 3D filtering，3维块匹配滤波）可以说是当前效果最好的算法之一。该算法的思想跟NL-Means有点类似，也是在图像中寻找相似块的方法进行滤波，但是相对于NL-Means要复杂得多，理解了NL-Means有助于理解BM3D算法。BM3D算法总共有两大步骤，分为基础估计（Step1）和最终估计（Step2）：

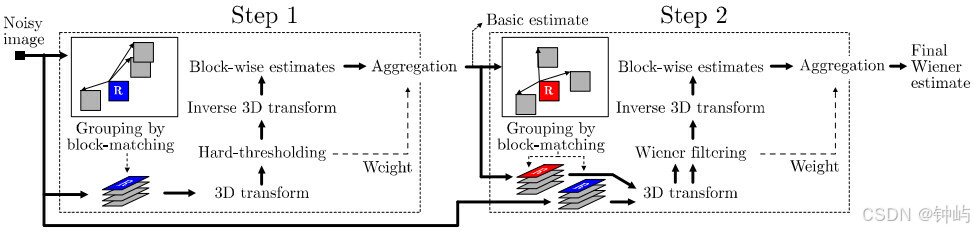
请添加图片描述
在这两大步中，分别又有三小步：相似块分组（Grouping），协同滤波（Collaborative Filtering）和聚合（Aggregation）。上面的算法流程图已经比较好地将这一过程表示出来了，只需要稍加解释。
Stpe1：基础估计
(1) Grouping：有了NL-Means的基础，寻找相似块的过程很容易理解。首先在噪声图像中选择一些 $\times k$ 大小的参照块（考虑到算法复杂度，不用每个像素点都选参照块，通常隔3个像素为一个不长选取，复杂度降到1/9），在参照块的周围适当大小（ $\times n$ ）的区域内进行搜索，寻找若干个差异度最小的块，并把这些块整合成一个3维的矩阵，整合的顺序对结果影响不大。同时，参照块自身也要整合进3维矩阵，且差异度为0。寻找相似块这一过程可以用一个公式来表示： $\{ Q:d(P,Q) \le {\tau ^{step1}}\} .$

d(P,Q)代表两个块之间的欧式距离。最终整合相似块获得的矩阵就是流程图Step1中左下角的蓝色R矩阵。

请添加图片描述
(2) Collaborative Filtering：形成若干个三维的矩阵之后，首先将每个三维矩阵中的二维的块（即噪声图中的某个块）进行二维变换，可采用小波变换或DCT变换等，通常采用小波BIOR1.5。二维变换结束后，在矩阵的第三个维度进行一维变换，通常为阿达马变换（Hadamard Transform）。变换完成后对三维矩阵进行硬阈值处理，将小于阈值的系数置0，然后通过在第三维的一维反变换和二维反变换得到处理后的图像块。这一过程同样可以用一个公式来表达： $T_{3Dhard}^{ - 1}(\gamma (T_{3Dhard}(Q(P)))).$

在这个公式中，二维变换和一维变换用一个 $T_{3Dhard}$ 来表示。 $\gamma$ 是一个阈值操作： $\gamma(x) = \begin{cases} 0, & \text{if } |x| \leq {\lambda_{3D}}\sigma \\ x, & \text{otherwise} \end{cases}$

$\sigma$ 是噪声的标准差，代表噪声的强度。

(3) Aggregation：此时，每个二维块都是对去噪图像的估计。这一步分别将这些块融合到原来的位置，每个像素的灰度值通过每个对应位置的块的值加权平均，权重取决于置0的个数和噪声强度。

Step2：最终估计
(1) Grouping：第二步中的聚合过程与第一步类似，不同的是，这次将会得到两个三维数组：噪声图形成的三维矩阵 ${Q^{basic}}(P)$ 和基础估计结果的三维矩阵 $Q (P)$ 。

(2) Collaborative Filtering：两个三维矩阵都进行二维和一维变换，这里的二维变换通常采用DCT变换以得到更好的效果。用维纳滤波（Wiener Filtering）将噪声图形成的三维矩阵进行系数放缩，该系数通过基础估计的三维矩阵的值以及噪声强度得出。这一过程同样可以用一个公式来表达： $T_{3Dwein}^{ - 1}(w_p \cdot {T_{3Dwein}}(Q(P))).$

在这个公式中，二维变换和一维变换用一个 $T_{3Dwein}$ 来表示。 $w_p$ 是一个维纳滤波的系数： ${w_p}(\xi ) = {{{{\left| {\tau _{3D}^{wien}({Q^{basic}}(P))(\xi )} \right|}^2}} \over {{{\left| {\tau _{3D}^{wien}({Q^{basic}}(P))(\xi )} \right|}^2} + {\sigma ^2}}}$

$\sigma$ 是噪声的标准差，代表噪声的强度。

(3) Aggregation：与第一步中一样，这里也是将这些块融合到原来的位置，只是此时加权的权重取决于维纳滤波的系数和噪声强度。

经过最终估计之后，BM3D算法已经将原图的噪声显著地去除。可以来看一组结果：

请添加图片描述

该算法的主要运算量还是在相似块的搜索与匹配上，在与NL-Means同样大小的相似块和搜索区域的情况下，BM3D的算法复杂度是要高于NL-Means的，应该大概在NL-Means的3倍左右。梦想着实时处理的同学可以死心了。
综上：

BM3D算法详解

BM3D（Block-Matching and 3D filtering）是一种高效且广受赞誉的图像去噪算法，首次提出于2007年。它通过利用图像中的非局部相似性（non-local similarity），即图像中存在许多外观类似的块（patches），来实现卓越的降噪效果，并在保留图像细节方面表现出色。

BM3D的基本步骤

BM3D算法通常分为两个主要阶段：初步估计（Hard Thresholding Step） 和 最终估计（Wiener Filtering Step）。

1. 初步估计（Hard Thresholding Step）

块匹配：遍历整张图像，提取大小为 N x N 的小块（例如8x8像素）。对于每个参考块，在一定搜索窗口内寻找与其最相似的其他块。相似性度量基于欧几里得距离或相关系数。
分组（Grouping）：找到的相似块被堆叠成一个三维矩阵，称为“群”或“group”。每个群由多个相似的二维块组成，形成第三维度。
变换与阈值处理：对每个群应用3D离散余弦变换（3D-DCT）。这一步将数据从空间域转换到频率域，在那里更容易识别哪些成分属于信号，哪些属于噪声。接着，通过设置适当的阈值去除高频噪声成分，即硬阈值化（hard thresholding）。
逆变换与聚合：对经过阈值处理后的群进行3D反向离散余弦变换（3D-IDCT），再将结果投影回原始位置，得到初步去噪后的图像。

2. 最终估计（Wiener Filtering Step）

重新分组：基于初步估计的结果，再次执行块匹配和分组操作。因为已经有一个较为干净的版本作为参考，所以能够更加准确地识别相似块。
维纳滤波：为了进一步提高去噪效果，这次使用了更加精细的滤波方法——维纳滤波。它考虑到了信号和噪声的统计特性，以最小化均方误差为目标，从而实现更好的降噪效果。
权重聚合：完成维纳滤波后，需要将所有修改过的块重新放置到它们原来的位置上，并考虑到不同块之间可能存在的重叠区域。为此，BM3D引入了一种加权方案，确保每个像素点的最终值是由其周围所有相关块共同贡献的结果。

BM3D的特点与优势

非局部自相似性：充分利用图像内部存在的重复模式，即使在复杂的自然场景中也能找到足够多的相似结构，使得去噪更加有效。
多尺度分析：不仅可以应用于单个尺度上的块，还可以扩展到多尺度框架下，进一步提升去噪性能。
高效性与灵活性：尽管BM3D是一个计算密集型算法，但它可以通过并行计算等方式加速执行。此外，由于其模块化的结构设计，BM3D很容易与其他技术结合，比如与深度学习相结合，形成新的混合模型。
良好的视觉质量：能够在去除噪声的同时很好地保持图像的边缘和其他重要特征，避免了过度平滑的问题。

应用领域

BM3D广泛应用于各种图像处理任务中：

医学影像：如MRI、CT扫描等，BM3D有助于提高诊断图像的质量。
卫星遥感：改善从太空拍摄的地表图像，帮助科学家更好地分析地理信息。
数字摄影：增强消费级相机拍出的照片质量，特别是在低光照条件下。
视频处理：用于电影和电视内容的后期制作，减少录制过程中产生的随机噪声。

总结

BM3D作为一种经典的图像去噪算法，以其卓越的性能和广泛的适用性成为了图像处理领域的标杆之一。它不仅在理论上有着坚实的数学基础，而且在实际应用中也证明了其价值。随着计算机硬件的发展和技术的进步，BM3D及其变体将继续在更多领域发挥重要作用。

算法比较

要比较算法效果，必然离不开评价体系。由于人带有主观因素，每个人的评价可能都不一样，因此有必要用几种客观的评价方法来对结果进行评价。目前，用得比较多的评价方式是MSE(Mean-Squared Error，均方误差)和PSNR(Peak Signal-to-Noise Ratio，峰值信噪比)。

两幅 $\times N$ 大小的图像 $u (x, y)$ 和 $v (x, y)$ 的MSE计算公式如下： ${e_{MSE}} = {1 \over {MN}}\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {{{[u(n,m) - v(n,m)]}^2}} } .$

在这个公式里没有表现出像素值范围对结果的影响，同样的均方误差8-bit的图像和12-bit的图像显然没有可比性。因此，又引入了峰值信噪比： $10{\log _{10}}{{{e_{MSE}}} \over {{s^2}}}.$

上式中， $s$ 是图像像素最大值，对于8-bit的图像而言 $s$ =255，PSNR的单位是分贝(dB)。通常 PSNR 值越高表示品质越好，一般而言，当 PSNR<30dB 时，代表以人的肉眼看起来是不能容忍的范围。因此大部分PSNR值都要>30dB。但PSNR高，并不代表图像质量一定好，有时候还是必须要靠人的肉眼去辅助判断图像的质量才较为正确。

不同PSNR对应的视觉效果
我对上面两种方法获得的结果针对原图计算了PSNR，结果如下：

两个算法的PSNR比较
NL-Means 32.0913
BM3D 33.6711

NL-Means和BM3D可以说是目前效果最好的去噪算法，其中BM3D甚至宣称它可以得到迄今为止最高的PSNR。从最终的结果也可以看出来，BM3D的效果确实要好于NL-Means，噪声更少，能够更好地恢复出图像的细节。在效果这一点上BM3D胜。无愧于State-of-the-art这一称号。当然，这里进行测试的样本比较少，可能还不足以完全说明问题。

本文的参考链接