相位解包裹::多频外差法＜保姆级别推导＞

结构光三维重构::相位解包裹(多频外差法)

优质博客链接：

结构光相移法-多频外差原理+实践（上）
相位解包裹（四）两类相位解包裹算法

前言：

​ 自己能力有限啊，看别人写的原理和公式总是觉得一知半解，根本原因是很多论文以及博客给出的公式中间过程都省略了，这让我很苦恼，所以很希望找到一个保姆级别博客。我相信有这种想法的人肯定不止我一人，所以我根据大佬的论文和博客，结合自己的理解，把多频外差法的公式原理一步步推导过程分享给大家！

一、问题提出

​ 以李中伟博士论文中四步相移为例，通过四步相移算法，计算出相位主值：

​ 相移法计算的相位主值如图所示：

​ 从图中可以看出，相位主值$\varphi （x,y)$对应有有多个x解（y对应多个x解)，此时的相位主值在整个测量空间不唯一，由此通过相位主值来确定位置坐标就无法实现，需要找到一种算法去确定相位主值处在哪个周期内，即n=?。

二、解决方法：多频外差法

思路：只要在光栅视野范围内，只存在一个周期，那么相位值与坐标就一一对应了。

实现：已知多个频率的条纹其对应的相位主值，通过不同频率的相位主值相差构造出更低频率的假想条纹，通过调整条纹的频率，使得一个周期占用的像素数（可以理解为波长）大于等于整个视场，那么就可以通过相位来获得唯一的坐标值(x或者y值).

（1）外差原理

​ 外差原理是指将两种频率不同的相位函数${\varphi }_1(x,y)$ 和${\varphi }_2(x,y)$叠加得到一种频率更低的相位函数${\varphi }_{1}2(x,y)$。

博客和论文的原理图：（如侵权联系我删除）

我的理解:

两个频率的相位差：

这个表达式等价于（在图上表达）蓝色和紫色表示的函数相减，即：

是不是很直观，一目了然！ 写代码就用表达式（1），理解就结合我画的图和表达式（2)，简直白给！

接着计算新条纹的波长：

当n1与n2同时取0时：

根据相似三角形：

（2）多频外差

先理解一个重要概念：空间频率(spatial frequency)，又称波数(wavenumber)，其定义是图像函数在单位长度上重复变化的次数。
以三频率外差为例，根据定义，频率可以理解成：

其中公式中的L为条纹方向的空间长度，即视场
所以根据波长的定义，可以计算出三个频率的实际波长，在图像上理解成单个周期占用的像素数

根据外差原理，可以计算出新的波长为：

从这里可以看出，最终三个频率可以得到一个波长等于L的合成条纹，即波长恰好占满整个视场，那么就成功解决了相位值和坐标值一一对应的难点，整个光栅范围内，只存在一个周期！

（以上是我个人理解，特别是空间频率不知道用的是否合适，大家参考即可！）

（3）最高频的相位解包裹

目的：计算出相位主值的所在的周期数n，恢复最高频条纹的连续相位，也就是解包裹。（下图蓝色即为相位展开后）

原因：选择越高频率的条纹进行相位解包裹，信噪比越大，精度越好。

想要求最高频率的周期数，可以结合以下图理解：

红色虚线对应两个三角形，其中：

可以求得频率1解包裹后的相位：

那么周期数n1可以得到,用展开的相位除以一个周期（2pi）：

注：round（）是四舍五入函数，为啥是四舍五入而不是向下取整我还妹整明白，等之后搞懂了再来记录。

最高频率的展开相位：

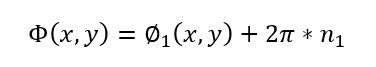
终于编辑完了！

声明：作者水平有限，如有错误，务必留言指正，共同学习进步！（如有帮助，不妨点赞评论。）