【多目标进化优化】 Pareto 最优解集的构造方法

1. 构造 Pareto 最优解的简单方法

1.1 Deb 的非支配排序方法

\quad\quad 设进化群体为 $P$，同时设置一个构造集 $P^{\prime }$。算法开始时将第一个个体放人构造集 $P^{\prime }$ 中，依次将进化群体 $P$ 中的个体 $p（p\notin P^{\prime }）$ 取出并放人构造集 $P^{\prime }$ 中(注意:此时放人 $P^{\prime }$ 中的个体只是临时的，因为有可能在随后的比较中被删除)，同时将当前取出的 $p$ 依次与 $P^{\prime }$ 中所有个体进行比较，删除 $P^{\prime }$ 中所有被力支配的个体，若个体力被 $P^{\prime }$ 中任意一个个体所支配，则将 $p$ 从 $P^{\prime }$ 中删除。具体过程如算法 3.1 所示

1.2 用排除法构造非支配解

\quad\quad 将进化群体 $Pop$ 中的每个个体 $X$ 依次与非支配集 $NDSet$ （开始时为空）中的个体 $Y$ 比较，如果 $X$ 支配 $Y$ ，说明 $Y$ 是被支配个体，将 $Y$ 从$NDSet$ 中删除（即排除掉）。 如果 $X$ 不被 $NDSet$ 中任何一个个体所支配，则将 $X$ 并入 $NDSet$ 中。当 $NDSet$ 为空（初始）时，直接将 $X$ 并入 $NDSet$ 中。具体过程如算法 3.2 所示

\quad\quad 值得说明的是，算法结束之前 $NDSet$ 中的个体不一定是非支配的。例如，设当前非支配集 $NDSet=[Y_1,Y_2,\dots ，Y_k]$, 进化群体 $Pop$ 中尚未参与非支配集个体比较的个体集设为 $Po{p}^{{}^{\prime }}=[X_{r+1}，X_{r+2},\dots ，X_n]$, $\forall Y\in NDSet,\exists X\in Po{p}^{{}^{\prime }}$, $Y$ 有可能受 $X$ 的支配； 此时 $NDSet=[Y_1,Y_2,\dots ，Y_k]$ 是 $[X_1，X_2,\dots ，X_r]$ 的非支配集.但不是 $[X_{r+1}，X_{r+2},\dots ，X_n]$ 的非支配集

\quad\quad 上述两种算法总结： 第一种算法是存在一个空的构造集，依次遍历 Pop，一个一个放进构造集内，每次放进后就与其他个体进行比较，对支配的个体进行删除操作。第二种算法则是将 Pop 中的每个个体与非支配集 NDSet 中的个体进行比较，若 NDSet 中的个体被支配，则删除，并且满足新个体不被 非支配集 NDSet 中的任何一个个体支配，则将此个体添加入非支配集 NDSet 中。很明显，第二种算法缺少了很多的删除操作。综上，第 2 种算法效率高于第 1 种

1.3 用排除法构造非支配解

\quad\quad 将构造集与非支配集分开，初始时设构造集 $NDSet1$ 为进化群体 $Pop$ ,非支配集 $NDSet$ 为空。将构造集 $NDSet1$ 中不同个体 $X$ 依次与其他个体 $Y$ 比较（包括构造集中除自身外的个体以及非支配集中个体），若 $X$ 支配 $Y$，则将 $Y$ 从构造集 $NDSet1$ 中清除；在一轮比较后若 $X$ 不被任何其他个体支配，则 $X$ 是非支配的，将 $X$ 并人非支配集 $NDSet$ 中。具体实现如算法 3.3 所示：这种方法不同于算法 3.2，无论在任何时候，$NDSet1$ 中的 个体一定是非支配的

2 用庄家法则构造 Pareto 最优解集

2.1用庄家法则构造非支配集的方法

\quad\quad 庄家法则是一种非回溯的方法，它每次构造新的非支配个体时不需要与已有的非支配个体进行比较，每一轮比较在构造集中选出一个个体出任庄家（一般为当前构造集的第一个个 体），由庄家依次与构造集中其他个体进行比较，并将庄家所支配的个体淘汰出局；一轮比较后，如果庄家个体不被任何其他个体所支配，则庄家个体即为非支配个体，否则庄家个体在该轮比较结束时也被淘汰出局。按照这种方法进行下一轮比较，直至构造集为空。

\quad\quad 定义3.1 $\forall x,y\in P$，若 $x$ 和 $y$ 之间不存在支配关系，则称 $x$ 和 $y$ 不相关或无关

\quad\quad 定义3.2 对于给定个体 $x\in P$，若 $\neg \exists y\in P$，使得 $y\succ x$ ($y$ 支配 $x$) 则称 $x$ 为集合 $P$ 的非支配个体。 由所有 $P$ 的非支配个体组成的集合称为 $P$ 的非支配集。

\quad\quad 定义3.3 设 $NDSet$ 是 $P$ 的非支配集，$NDSet\subset P$ , $\forall x\in P$,若 $x$ 是 $P$ 的非支配个体，必有 $ x \in NDSet$，则称 $NDSet$ 是 $P$ 的最大非支配集

\quad\quad 定义3.4 若在 $P$ 中不存在任何其他 $x$ 比 $x^{\ast }$ 更小，即 $\neg \exists x\in P$，使得 $x\succ x^{\ast }$ ($z$ 支配 $x^{\ast }$)则称是 $x^{\ast }$ 偏序集 $（P，\succ ）$ 中的最小元素。所有最小元素的集合表示为 $M(P，\succ )$。设 x ∈ M ( P ， ≻ ) , C l u s t e r ( x ) = { y ∣ x ≻ y x \in M(P，\succ), Cluster(x) = \{y|x \succ y x∈M(P，≻),Cluster(x)={y∣x≻y,y \in P}$ 是以7为最小元的族。

\quad\quad 设 $P$ 为一进化群体，$Q$ 为构造集，初始时 $Q=P,NDSet$ 为非支配集，初始时为空。 从 $Q$ 中任取一个个体，依次与所有其他个体比较（包括构造集中除自身外的个体以及非支配集中个体），将被该个体所支配的个体从 $Q$ 中删除， 如果该个体没有被其他任何一个个体所支配，则它是非支配的，将它并入非支配集 $NDSet$ 中，否则也从 $Q$ 中清除该个体；以此下去，直至 $Q$ 为空。

\quad\quad 构造集合P的非支配集的方法可描述如下：
\quad\quad ① 设 $Q$ 为构造集，初始时 $Q=P$； $NDSet$ 为 $P$ 的非支配集，初始时 $NDSet=\varnothing$；
\quad\quad ② 从 $Q$ 中取一个体 $x$，令 Q = Q − { x } Q=Q-\{x\} Q=Q−{x}（即将 $x$ 从 Q 中去掉），$D=\varnothing$；
\quad\quad ③ 令 D = D ∪ { y ∣ x ≻ y , y ∈ P } D = D \cup \{y|x \succ y,y \in P \} D=D∪{y∣x≻y,y∈P}（找出 $P$ 中所有被 $x$ 支配的个体，放入集合 $D$ 中）
\quad\quad ④ 令 $Q=Q-D$，若 $\neg \exists z\in Q$，使得 $z\succ x$ ($z$ 支配 $x$) ，则令 N D S e t = N D S e t ∪ { x } NDSet = NDSet \cup \{x\} NDSet=NDSet∪{x}（再将 $D$ 从 $Q$ 中去掉，如果 $Q$ 中不存在能支配 $x$ 的个体，则将 $x$ 放入非支配集中）
\quad\quad ⑤ 重复步骤 ②~④，直至 Q 为空

庄家法合理性证明（感兴趣的可以了解） 庄家法时间复杂度分析（感兴趣的可以了解） 庄家法实例分析

非支配层级关系说明

$P_1$ 表示第一层非支配集，即当全部个体参与算法时，所筛选出来的非支配集，$P_2$ 表示如果去掉 $P_1$ 中的所有个体，然后将剩余个体参与算法所筛选出来的非支配集，$P_3，P_4$ 以此类推

注： 后面递归构造 Pareto 最优解集时，会涉及到非支配层级关系的分类

3. 上述三个算法的 CPU 时间和处理效率比较

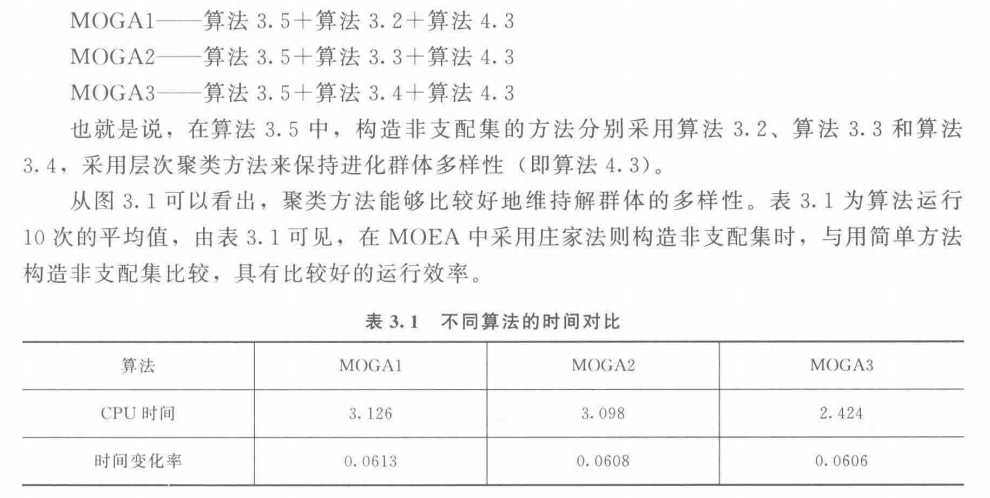
4. 用擂台赛法则构造 Pareto 最优解集

\quad\quad 利用庄家法则构造非支配集时，虽然没有回溯，这在一定程度上提高了构造非支配集的速度，但每一轮比较不一定能构造岀一个新的支配个体。下面讨论的擂台赛法则,每一轮比较均能构造出一个新的非支配个体，因此擂台赛法则比庄家法则具有更高的构造非支配集的效率

\quad\quad 当用擂台赛法则构造一个进化群体的 $Pareto$ 最优解集时，每次搜索新的非支配个体时不需要与已有的非支配个体进行比较，每一轮比较时在构造集中选出一个个体出任擂台主 （一般为当前构造集的第一个个体），由擂台主与构造集中其他个体进行比较，败者被淘汰出局,胜者成为新的擂台主，并继续该轮比较；一轮比较后，最后的擂台主个体即为非支配个 体。按照这种方法进行下一轮比较，直至构造集为空。

4.1 用擂台赛法则构造非支配集的方法

• 注：一轮比较中，擂台赛只有在最后一位擂台主留下后再去掉被最后一位擂台主所支配的个体，在擂台主进行交替的过程中不去掉，可以提高效率

擂台法合理性证明和时间分析 擂台法实例分析

5. 用递归方法构造 Pareto 最优解集

运用了分治的思想，划分为两个部分进行处理

当优化问题只有两个目标时，特殊处理，无须进行递归调用，如下：

代码逻辑解释

\quad\quad 首先，前面已经排好非支配层级关系，排到了 $F_A$，即已有 $A$ 个层级关系了，$if(s_i\ngtr F_A)$ ：若新个体 $S_i$ 不被最后一个层级 $F_A$ 中任意一个个体所支配，说明新个体最差的情况也能插入到 $F_A$ 这个层级中，此时，找出 $F_1,F_2,...,F_A$ 中的 $F_b$ 使得新个体 $S_i$ 不支配 $F_b$ 中的任何一个个体，且标号 $b$ 最小，也即找到一个对 $S_i$ 来说最好的非支配集然后将 $S_i$ 加入进去。否则说明当前情况的最后一层，即 “最不靠谱，级别最低” 的 $F_A$ 层都存在能够支配 $S_i$ 的个体，就需要重新创建一个层级即 $A=A+1$ 操作，将 $S_i$ 放进去，此时最后一个层级就变为了仅有一个个体 $S_i$ 的非支配集

当有两个以上目标时，如下：

\quad\quad Jensen 基于分治技术，采用递归的方法提出了一类构造非支配集的算法，其中 N 为进化群体的规模，M 为目标数。算法 3.7 中，假定在同一目标上没有相同的值，主过程 Non-dominated-sort(S，M）带两个参数，其中 S 为进化群体，M 为目标数。在主过程中（算法 3.7 （a))，对每个个体 $s\in S$ 设置一个函数值 $f[s]$，用于表示该个体所对应的边界层次（即对应的非支配层级）。初始时将 $f[s]$ 的值均置为1，即在初始时认为 S 中所有个体均在第一层边界上。通过调用 ND-helper _ A(S，M) (算法3.7 (b))，使 $f[s]$ 返回个体 $s$ 所对应的边界层次。显然，所有 $f[s]=1$ 的个体 $s$ 均为非支配的。

\quad\quad 在递归过程 ND-helper_ A(S， M) 中（算法3.7 (b) ），$S$ 为进化群体，M 为目标数，M 个子目标分别表示为 $x_1,x_2,...,x_M$ （注意这里是用 $x$ 来表示每个目标函数，并不是 $f$ ）。当 $S$ 中只有两个个体时(即 $|S|=2$ )， 则将这两个个体进行比较。若 $s_1$ 支配 $s_2$，则令 $f[s_2]=max(f[s_1]+1,f[s_2])$,若 $s_2$ 支配 $s_1$ ,则令 $f[s_1]=max(f[s_2]+1,f[s_1])$。 当 $S$ 中个体大于 $2$ 时，则将 $S$ 分割为两个大小相等的子集 $L$ 和 $H$ ，即 $set(L，H)=split(S,x_M^{split}，M)$。分割时，取第 $M$ 个目标的中值 $x_M^{split}$ (也就是所有个体对应最后一个函数 $M$ 目标值的平均值) ，然后将所有第 $M$ 个目标值小于等于 $x_M^{split}$ 的个体放入 $L$ 中，高于 $x_M^{split}$ 的则放入 $H$ 中。由此可知，$L$ 中的任何一个个体均不被 $H$ 中个体所支配，因为有 $\forall s_1\in L\wedge \forall s_2\in H=>x_M(s_1)<x_M(s_2)$ 。这样，通过进一步递归调用 ND-helper_ A(L，M) 来构造 $L$ 的非支配集，且在构造 $L$ 的非支配集时就不需要考虑 $H$（因为 $H$ 中的所有个体第 $M$ 个目标函数对应的目标值均比 $x_M^{split}$ 大，而 $L$ 中的均比 $x_M^{split}$ 小，所有 $H$ 中的个体要么被 $L$ 中的个体支配，要么互不支配），但在构造 $H$ 的非支配集时必须考虑 $L$， 因为 $H$ 中的个体有可能不被 $L$ 中的个体所支配，所以可能存在 $L$ 中的个体与 $H$ 中的个体处在同一非支配层级。要判断 $s2\in H$ 是否被 $s1\in L$ 支配，需要调用 ND-helper_B(L, H, M一1)（算法3.7(c)）来比较 $L$ 和 $H$ 在前 $(M一1)$ 个子目标上的支配关系。若 $s\in L$ 支配 $s2\in H$，则令 $f[s_2]=max(f[s_1]+1，f[s_2])$。此外，还需要判断 $H$ 中个体是否被 $H$ 中其他个体所支配，因此需要调用 ND-helper_A(H，M)

ND-helper_A(S，M)：为 S 个个体划分支配层级 ND-helper_ B(L， H，M)：用于判断前 M-1 个个体的支配关系，具体流程如下：

\quad\quad 在递归过程 ND-helper_ B(L， H，M)中（算法3.7 (c)），通过对 $H$ 中个体与 $L$ 中个体进行比较，从而实现对 $H$ 中个体进行分类(注意：这只是部分分类，要在此语句后调用 ND-helper_ A(H, M)，才能实现对 $H$ 的完全分类)。若 $L$ 或 $H$ 中只有一个个体，则将 $H$ (或 $L$ )中所有个体与 $L$ (或 $H$)中这(唯一的)一个个体比较，如果 $s_1\in L$ 支配 $s_2\in H$，则令 $f[s_2]=max(f[s_1]+1，f[s_2])$。如果此时 $M=2$，则直接调用一个二维分类算法(类似算法3.8)，通过与 $L$ 中个体比较其支配关系，给 $H$ 中个体分配边界数(即调整 $f[s]，s\in H$)，即如果 $s_1\in L$ 支配 $s_2\in H$，则令 $f[s_2]=max(f[s_1]+1，f[s_2])$。

\quad\quad 在其他的过程中，处理要复杂一些

\quad\quad ① 如果 $max(x_M(l_1)，...x_M(l_{|L|}))\le min(x_M(h_1)，...x_M(h_{|H|})$，表明在第 $M$ 个目标上，$L$ 中个体比 $H$ 中个体具有小的值。则直接调用 ND-helper_ B(L, H, M - 1)。（此时 $L$ 在第 $M$ 个目标肯定是整体支配 $M$ 的，所以只需继续比较前 M - 1 个目标的情况）

\quad\quad ② 如果 $min(x_M(l_1),...,x_M(l_{|L|}))>max(x_M(h_1)，...x_M(h_{|H|})$，表明在第 $M$ 个目标上，$H$ 中个体比 $L$ 中个体具有小的值，这种情况下算法不需要做任何处理。

\quad\quad ③ 如果 $max(x_M(l_1),...,x_M(l_{|L|}))>min(x_M(h_1)，...x_M(h_{|H|})$，且 $min(x_M(l_1),...,x_M(l_{|L|}))\le max(x_M(h_1)，...x_M(h_{|H|})$，表明在第 $M$ 个目标上，$H$ 中部分个体的值比 $L$ 中个体小，同时 $H$ 中部分个体的值又比 $L$ 中个体大，即 $H$ 中个体与 $L$ 中个体的大小关系存在着交迭，这种情况下，需要在 $H$ 或 $L$ 中针对第 $M$ 个目标选取一个中值 $x_M^{split}$，并将 $H$ 分割为 $H_1$ 和 $H_2$，将 $L$ 分割为 $L_1$ 和 $L_2$。然后分别递归调用 ND-helper _ B($L_1$, $H_1$, M)、ND-helper_ B($L_1$, $H_2$, M-1) 和 ND-helper_ B($L_2$, $H_2$, M)。值得说明的是，这里不需要针对 $L_2$ 来调整 $H_1$，即不需要调用 ND-helper_ B($L_2$, $H_1$, M)，是因为 $H_1$ 中的个体不可能被 $L_2$ 中的个体所支配。

6. 用快速排序方法构造 Pareto 最优解集

6.1 个体之间的关系

\quad\quad 性质 3.1 \quad 如果 $x$ 和 $y$ 不相关，且 $y\succ z$，则要么 $x\succ z$ 要么 $x$ 和 $z$ 不相关

\quad\quad 性质3.2 \quad 如果 $x\succ y$，且 $y$ 和 $z$ 不相关，则要么 $x\succ z$，要么 $x$ 和 $z$ 不相关。

\quad\quad 性质3.3 \quad 非支配集中的不同个体之间是彼此不相关的（废话）

\quad\quad 定义 3.5 \quad $\forall x,y\in Popx{\succ }_{d}y$，表示 $x\succ y$ 或者 $x$ 与 $y$ 不相关两种情况

\quad\quad 性质 3.4 \quad 关系 “${\succ }_d$” 不具备传递性

\quad\quad 性质 3.5 \quad 关系 “$\succ$” 具备传递性

\quad\quad 性质 3.5 \quad 设 $Pop=y_1,y_2,...,y_m,\forall x\in Pop,x$ 将 $Pop$ 分为两部分， { x 1 , x 2 , . . . , x k } \{x_1, x_2, ..., x_k\} {x1​,x2​,...,xk​} 和 { x k + 2 , x k + 3 , . . . , x m } \{x_{k +2}, x_{k +3}, ..., x_{m}\} {xk+2​,xk+3​,...,xm​}, 使 ∀ y ∈ { x 1 , x 2 , . . . , x k } , ∀ z ∈ { x k + 2 , x k + 3 , . . . , x m } \forall y \in \{x_1, x_2, ..., x_k\}, \forall z \in \{x_{k +2}, x_{k +3}, ..., x_{m}\} ∀y∈{x1​,x2​,...,xk​},∀z∈{xk+2​,xk+3​,...,xm​}，有 $y{\succ }_{d}x$，且 $x\succ z$，则：（注意 $x$ 为单个个体，将 $Pop$ 分为了 $y$ 和 $z$）

\quad\quad ① { x k + 2 , x k + 3 , . . . , x m } \{x_{k +2}, x_{k +3}, ..., x_{m}\} {xk+2​,xk+3​,...,xm​} 中的个体均为支配的

\quad\quad ② 若 ∀ y ∈ { x 1 , x 2 , . . . , x k } \forall y \in \{x_1, x_2, ..., x_k\} ∀y∈{x1​,x2​,...,xk​}，$x$ 不被 $y$ 支配，则 $x$ 是 $Pop$ 的非支配个体。（$x$ 支配 $z$，$x$ 又 不被 $y$ 支配，肯定是 $Pop$ 的非支配个体了）

\quad\quad ③ ∀ y ∈ { x 1 , x 2 , . . . , x k } \forall y \in \{x_1, x_2, ..., x_k\} ∀y∈{x1​,x2​,...,xk​}，若 $y$ 是 { x 1 , x 2 , . . . , x k } \{x_1, x_2, ..., x_k\} {x1​,x2​,...,xk​} 的非支配个体，则 $y$ 也是 $Pop$ 的非支配个体。（很好理解，此时 y 是 { x 1 , x 2 , . . . , x k } \{x_1, x_2, ..., x_k\} {x1​,x2​,...,xk​} 中的一个个体，由于原本 $y$ 要么支配 $x$，要么与 $x$ 不相关，但 $x$ 支配 $z$，所以由支配的传递性，$y$ 也支配 $z$，两边合并起来，便是 $Pop$ 所以 $y$ 支配 $Pop$）

\quad\quad 性质 3.6 \quad 按照关系 “${\succ }_d$” ，用快速排序算法排序后的有序序列，第一个个体是非支配的。

\quad\quad 定理 3.2 \quad 设 P o p = { x 1 , x 2 , . . . , x n } Pop = \{x_1, x_2, ..., x_n\} Pop={x1​,x2​,...,xn​}, 对 $r$ 个目标按照关系 “${\succ }_d$” 用快速排序算法排序后的有序序列为 { y 1 , y 2 , . . . , y n } \{y_1, y_2, ..., y_n\} {y1​,y2​,...,yn​}, 则 $\exists k$，使有序序列 { y 1 , y 2 , . . . , y k } \{y_1, y_2, ..., y_k\} {y1​,y2​,...,yk​} 为 $Pop$ 的非支配集

\quad\quad 定理 3.3 \quad 设 P o p = { y 1 , y 2 , . . . , y n } Pop = \{y_1, y_2, ..., y_n\} Pop={y1​,y2​,...,yn​} 为按关系 “${\succ }_d$” 用快速排序算法排序后的有序序列， { y 1 , y 2 , . . . , y k } \{y_1, y_2, ..., y_k\} {y1​,y2​,...,yk​} 为 $Pop$ 的非支配集，则 ∀ y ∈ { y k + 1 , y k + 2 , . . . , y n } \forall y \in \{y_{k +1}, y_{k +2}, ..., y_n\} ∀y∈{yk+1​,yk+2​,...,yn​}， ∃ y ′ ∈ { y 1 , y 2 , . . . , y k } \exists y^{'} \in \{y_1, y_2, ..., y_k\} ∃y′∈{y1​,y2​,...,yk​}，使 $y^{{}^{\prime }}\succ y$

\quad\quad 定理 3.4 \quad 设 P o p = { y 1 , y 2 , . . . , y n } Pop=\{y_1, y_2, ..., y_n\} Pop={y1​,y2​,...,yn​}，为按关系 “${\succ }_d$” 用快速排序算法排序后的有序序列，存在 $k_1<k_2<\cdot \cdot \cdot <k_m$，使 P 1 = { y 1 , y 2 , . . . , y k 1 } ， P 2 = { y k 1 + 1 , y k 1 + 2 , . . . , y k 2 } , ⋅ ⋅ ⋅ , P m = { y k m − 1 + 1 , y k m − 1 + 2 , . . . , y k m } P_1=\{y_1, y_2, ..., y_{k_1}\}， P_2 = \{y_{k_1 + 1}, y_{k_1 + 2}, ..., y_{k_2}\}, ···, P_m = \{y_{k_{m-1} + 1}, y_{k_{m-1} + 2}, ..., y_{k_m}\} P1​={y1​,y2​,...,yk1​​}，P2​={yk1​+1​,yk1​+2​,...,yk2​​},⋅⋅⋅,Pm​={ykm−1​+1​,ykm−1​+2​,...,ykm​​}

\quad\quad ① ∪ P i ∈ { 1 , 2 , . . . , m } = P o p ; \cup P_{i \in \{1, 2, ..., m\}} = Pop; ∪Pi∈{1,2,...,m}​=Pop;

\quad\quad ② ∀ i , j ∈ { 1 , 2 , . . . , m } \forall i, j \in \{1, 2, ..., m\} ∀i,j∈{1,2,...,m}，且 $i\ne j,P_i\cap P_j=\varnothing ;$

\quad\quad ③ $P_1\succ P_2\succ \cdot \cdot \cdot \succ P_2$，即 $\forall y\in P_{i+1},\exists x\in P_i$，使 $x\succ y(i=1,2,...,m-1)$

用 ${\succ }_d$ 可以对多目标群体进行分类的实例说明：

6.2 用快速排序发构造非支配集

\quad\quad 这里采用快速排序的方法将非支配个体从进化群体中分类出来。如算法 3.9 所示，Quick-pass() 对表 $Pop[s..t]$ 进行一趟快速排序，并将支配 $Pop[s]$ 的个体或与 $Pop[s]$ 不相关的个体存放到 $Pop[s..i-1]$ 中，将被 $Pop[s]$ 支配的个体存放到 $Pop[i+\mathrm{1..}t]$ 中，$s\le i\le t$

快排的非递归实现 快排构造非支配解的实例

6.3 用改进的快速排序方法构造 Pareto 最优解集

改进后快排构造非支配解的实例

Reference

[1] 《多目标进化优化》. 郑金华. 邹娟著