1. 概述
\quad\quad 对一个多目标进化算法的性能进行评价时,一方面需要有一套能够客观地反应 MOEA 优劣的评价工具或方法;另一方面需要选取一组比较有代表性的测试问题,通常选取有已知解的问 (benchmark test problem) 作为测试用例,有关讨论可参见博客。对 MOEA 的评价主要考虑两个指标:一个是 MOEA 的效果 (effectiveness),另一个是 MOEA的效率(efficiency)。MOEA 的效果是指它所求得的 Pareto 最优解集的质量,主要是指 MOEA 的收敛效果和分布效果。MOEA 的效率主要指它在求取一个多目标优化问题的 Pareto 最优解集时所需要的 CPU 时间,以及它所占用的空间资源。此外,MOEA的鲁棒性、求解问题的范围,以及方便使用等也是考察 MOEA 性能的重要指标。有关MOEA 评价工具后面会详细介绍
\quad\quad 可以用两类不同的方法来评价 MOEA 的性能,一类是从理论上对 MOEA 的性能进行分析,另一类是采用实验的方法来对 MOEA 的性能进行测试和比较分析。 一个 MOEA 的运行效率和收敛特性是可以通过理论方法解决的,MOEA 设计者一般也对自己所设计的算法进行有关理论分析和论证。但目前对 MOEA 收敛性的论证主要局限于时间趋向于无穷大时算法的收敛性,对 MOEA 在有限时间内的收敛性分析结果极少。此外,当前大多数的 MOEA 所釆用的进化机制没有本质上的差异,故而很难从理论上判断哪个 MOEA 更好。因 此,目前多采用实验方法对 MOEA 的性能进行测试和比较分析。实践中,可以釆用理论分析与实验手段相结合的方法,来评价一个MOEA的性能。
\quad\quad 当釆用实验手段对 MOEA 进行性能测试时,往往具有一定的局限性。一方面是因为所选取的测试用例通常具有一定的局限性,另一方面是只能对有限的 MOP 进行测试。可见, 用枚举方法对 MOEA 的性能测试,不能够得岀诸如 “某某 MOEA 是最好的” 这样的结论。 因此,当采用实验手段对 MOEA 的性能进行测试时,重在对实验结果的比较与分析。例如,当一个 MOEA 对某类 MOP 表现出比其他 MOEA 更好的实验结果时,需要分析产生这个结果的原因。此外,为了使实验数据具有很好的说服力,实验过程的设计十分重要,一般地,一个好的实验过程应包括下列步骤(Barr et aL 1995):
\quad\quad ① 确定实验的目的
\quad\quad ② 选取合适的 MOEA 性能评价工具(或方法)
\quad\quad ③ 选取具有代表性的测试用例
\quad\quad ④ 实验及实验结果分析
\quad\quad ⑤ 采用合适的方式(如图和表)描述实验结果
\quad\quad 另外,在实验报告中,一定要比较清楚地说明所使用的实验环境,以便于实验结果的 再现。
2. 实验设计与分析
\quad\quad 科学实验无论对科学研究还是对工程实践都具有十分重要的作用。在设计实验时,设计者通常具有很大的自由度来决定诸如测试用例、MOEA 具体的实现方法、实验环境、 MOEA 性能评价工具、算法的参数设置,以及实验结果的描述等与实验有关的要素。这些实验要素的选取,对实验结果具有十分重要的作用和影响。因此,在确定各项实验要素时, 要考虑可行性,同时也要考虑公平和公正性。只有这样,才能使实验结果具有意义和价值。 下面对实验过程的主要环节进行讨论(Barret al, 1995)。
2.1 实验目的
\quad\quad MOEA 测试实验主要包括两个方面的内容,一是针对相同的测试问题对不同的 MOEA 进行比较实验,二是针对某个具体 MOEA 所做的关于它的性能特征的实验。对于比较实验,其目的在于比较一个新 MOEA 与已有 MOEA 的性能差异,所参照的 MOEA 应该是当前最具有代表性的。如 NSGA-II 、SPEA2、MOEA/D 等。通常可以考虑以下几个方面:
\quad\quad ① 与已有算法在收敛性、所求解集分布性方面的比较实验
\quad\quad ② 与已有算法在求解能力方面的比较实验。
\quad\quad ③ 与已有算法在鲁棒性方面的比较实验,如对所求解问题特征的敏感性、对待处理数据质量的敏感性、对不同参数设置的敏感性等。
\quad\quad ④ 与已有算法在应用范围方面的比较实验。
\quad\quad ⑤ 与已有算法在效率上的比较实验。
\quad\quad 对于 MOEA 的性能特征测试实验,主要目的在于通过实验获得 MOEA 的行为特征, 以及影响 MOEA 行为的参数。实验的具体内容类似于对比实验,只不过是这类实验更侧重于某个具体 MOEA 的性能描述。
2.2 MOEA 评价工具的选取
\quad\quad MOEA 的主要性能指标可以概括为 3 个方面:所求解集的质量、计算效率和鲁棒性。 对每一类性能指标,都有多种评价工具与之相对应。可以根据实验的目的来选取合适的评价工具,有关评价工具的详细讨论可参见第 3 节
\quad\quad 1. 所求解集的质量
\quad\quad 当运行一个 MOEA 后,它所求得的解集的质量是我们最关心的,因为这是最根本的东西。如果一个 MOEA 不能求得高质量的解集,那么该 MOEA 的其他性能无论有多么好, 也是没有意义的。
\quad\quad 评价解集质量时,对于有已知最优解的标准问题,如 benchmark 测试问题,通常的做法是比较所求解集与最优解集的偏差(deviation)。而对于那些没有已知最优解的优化问题, 可以釆用趋近度评价方法(Deb et al, 2002b),通过计算所求解集到参照集的最小距离来衡量,该距离越小,表明趋近程度越高。其中,参照集为历代非支配集并集的非支配集。当然,也可以与已公开发表的结果进行比较。
\quad\quad 2. 计算效率
\quad\quad 在确保所求解集质量的前提下,MOEA 的运行效率是考察的一项重要性能指标。可以用 MOEA 运行的 CPU 时间,也可以以关键操作的迭代次数来衡量 MOEA 的时间效率。在一个 MOEA 的收敛过程中,它所求解集的质量往往是随着时间的变化而变化的。一般情况下,解集的质量会随着时间的增加而变好,这一变化规律可以用 “质量-时间” 曲线来描述。 如果一个 MOEA 的鲁棒性不好,它的收敛性能可能是不稳定的,这在 “质量-时间” 曲线上 一定会表现出来。
\quad\quad 在考察一个 MOEA 的计算效率时,要注意区分几个不同的时间概念
\quad\quad ① MOEA 运行的终止时间、终止条件往往是人为设定的
\quad\quad ② MOEA 找到高质量解集所用的时间,这是通过对解集质量的评价后确定的
\quad\quad ③ MOEA 在一次迭代中不同的阶段所用的时间
\quad\quad 因为不同的 MOEA 所采用的进化策略、非支配集的构造方法等可能存在较大差异,对不同阶段的时间分析有利于深入研究 MOEA 的进化特性。
\quad\quad 3. 鲁棒性
\quad\quad 如果一个 MOEA 只对某一个具体问题具有很好的求解能力,那么这个 MOEA 称不上是鲁棒的。一个鲁棒的 MOEA 应该具有比较广泛的应用领域,且在求解领域问题时应具有很好的稳定性。一个 MOEA 对所求解问题特征的敏感性、对待处理数据质量的敏感性,以及对不同参数设置的敏感性等,也是衡量其鲁棒性的重要指标。如果一个 MOEA 不能求解具有不同特征的问题,那么它不是鲁棒的;如果它对于质量较差的输入数据或初始数据,不能得到理想的解或者收敛性能随之下降,这样的 MOEA 也不是鲁棒的;同样地,如果一个 MOEA 对于不同的参数设置,所求解集的质量和收敛性能具有较大的差异,那么该 MOEA 也不是鲁棒的。
2.3 实验参数设置
\quad\quad 在 MOEA 实验中,不同的参数设置可能会影响到它的性能。一般地,可能影响 MOEA 性能的因素主要有三个方面:测试问题中的参数、MOEA 自身的参数和实验环境参数。
\quad\quad 1. 测试问题中的参数
\quad\quad 一般地,不同的测试问题具有不同的特征。同类型的测试问题往往也因为问题规模的不同 (如决策变量的数量和目标函数的数量) 和数据表示方法的不同而影响 MOEA 的性能。 因此,在 MOEA 测试时应尽可能多地选取不同类型的测试用例,并对可能影响 MOEA 性能的不同参数设置运行 MOEA
\quad\quad 2. MOEA自身的参数
\quad\quad 不同的 MOEA 在进化策略、非支配集的构造方法等方面往往存在着较大的差异。对于同一个 MOEA,不同的参数设置也可能影响它的性能,如进化群体规模 (population size)、 限制交配操作 (mating restriction)、个体适应度值的分配策略 (fitness assignment)、共享机制(sharing mechanism),以及进化个体的表示 (individual representation) 等。针对不同的参数设置对同一个 MOEA 的测试,是 MOEA 参数敏感性分析的一个重要方面。
\quad\quad 3. 实验环境参数
\quad\quad 实验环境参数主要指 MOEA 运行的软件和硬件环境。硬件方面主要有机器的品牌、机 型、内存大小、CPU、处理器的个体,以及处理器的通信方式等。软件方面主要有操作系统、编程语言、编程语言的编译器及其设置等。此外,不同编程人员所完成的 MOEA 代码也有可能影响一个 MOEA 的性能。
2.4 实验结果分析
\quad\quad 完成实验后,一个很重要的工作就是实验结果分析。在分析时,针对预定的实验目的, 通过统计技术或非统计技术,将在实验中釆集到的数据进行整理并做出解释。考虑到 MOEA 运行过程中存在随机性,实验结果一般是 10〜30 次 MOEA 独立运行的平均结果。 分析时,要重点分析不同的参数设置对 MOEA 性能的影响,如目标数的增加对 MOEA 求解质量和效率的影响。尤其要注意对 “负结果” 的分析,例如,当一个 MOEA 对众多的 试问题具有很好的实验结果,但对某个测试问题的实验结果不理想,一定要对这样的 “负结果” 做出理性的分析。
\quad\quad 对实验结果进行分析时,比较直观的表现形式是图或表,如质量-时间、速度-鲁棒性 等,都可以用合适的图表形式直观地描述。
3. MOEA 性能评价方法
3.1 评价方法概述
\quad\quad 设计 MOEA 性能评价方法时,应该考虑以下特征:
\quad\quad ① 函数值的范围应当在 0〜1 之间,因为函数要用于不同代之间的比较,0〜1 之间的函数可以更方便地比较算法不同代之间的变化
\quad\quad ② 期望函数值应当是可知的,也就是说理论上的非支配集的分布度是可以计算出来的
\quad\quad ③ 评价曲线应当是随着代数的增加成递增或递减的,这样更有利于不同集合之间的比较
\quad\quad ④ 评价函数应适用于任意多个目标。尽管这不是绝对需要的,但这使得算法能在不同目标维上进行比较
\quad\quad ⑤ 函数的计算复杂度不能太高
\quad\quad 目前,研究者们已经提出了许多种 MOEA 性能评价工具或方法,归纳起来可以分为三大类:第一类用来评价所求解集与真正的 Pareto 最优面的趋近程度,主要用于评价 MOEA 的收敛性;第二类用来评价解集的分布性;第三类是综合考虑解集的收敛性和分布性,用来评价解的综合性能。
\quad\quad 要针对问题的特征,并根据实验目标在众多的评价方法中选取合适的评价方法。本小节将讨论一些具有代表性的评价工具或方法。
3.2 收敛性评价方法
\quad\quad 在理想情况下,MOEA 的求解过程是一个不断逼近最优边界,最终达到最优边界的过程。但在实际应用中,对于特別复杂的 MOP, MOEA 很难找到真正的 Pareto 最优面。也就是说,MOEA 并不能保证一定可以找到 Pareto 最优解,而是尽可能地找到一个很好的近似解。因此,如何判断一组近似解的好坏就变得非常重要。
\quad\quad 对 MOP 解集的趋近程度进行评价时,有两个参数非常重要: P F k n o w n PF_{known} PFknown 与 P F t r u e PF_{true} PFtrue ,即已知的 Pareto 面和真正的 Pareto 面,如图 10.1 所示。下面讨论几种具有代表性的趋近度评价方法,并对具体例子进行计算,虽然大部分例子都是在 2 维目标空间上的,但是这些评价方法是可以扩展到任意维空间的。
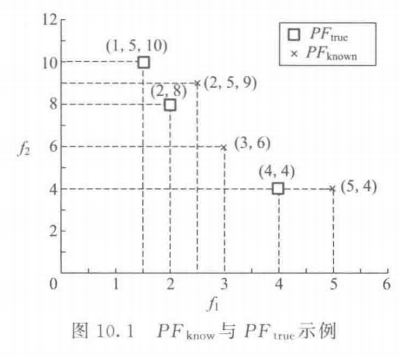
\quad\quad 1. 错误率
\quad\quad 运行一个 MOEA 后,得到 P F k n o w n PF_{known} PFknown,但可能存在某些解向量不在 P F t r u e PF_{true} PFtrue 中。如果存在这样的向量,那么说明这些向量是没有被覆盖的。定义没有被覆盖的解向量与群体规模的比率为错误率(error ratio, ER),表示如下(Coello Coello et al,2002):
E R ≜ ∑ i = 1 n e i n ER \triangleq \frac{\sum_{i=1}^n e_i}{n} ER≜n∑i=1nei
式中, n n n 是 P F k n o w n PF_{known} PFknown 中的向量数目, P F k n o w n = { X 1 , X 2 , . . . , X n } PF_{known} = \{X_1, X_2, ..., X_n\} PFknown={X1,X2,...,Xn}。 定义 e i e_i ei 如下:
e
i
=
{
0
,
若向量
X
i
∈
P
F
t
r
u
e
(
i
∈
{
1
,
2
,
.
.
.
,
n
}
)
1
,
否则
e_i = \begin{cases} 0, & \text{若向量 $X_i \in PF_{true}(i \in \{1, 2, ..., n\})$ } \\ 1, & \text{否则} \\ \end{cases}
ei={0,1,若向量 Xi∈PFtrue(i∈{1,2,...,n}) 否则
\quad\quad
例如,ER = 0 表明 MOEA 所求的
P
F
k
n
o
w
n
PF_{known}
PFknown 中,每一个向量都在
P
F
t
r
u
e
PF_{true}
PFtrue 中;
E
R
=
1
ER=1
ER=1 则表示没有一个向量在
P
F
t
r
u
e
PF_{true}
PFtrue 中。在图 10.1 中,根据错误率的定义,可以计算出其值为
E
R
=
2
/
3
ER = 2/3
ER=2/3。与之相似的方法有 Zitzler 等提出的采用参照集中非支配个体的比率来衡量算法的趋近程度。
\quad\quad 2. 两个解集之间的覆盖率
\quad\quad Zitzler 在 2000 年提出了一种评价方法 (Zitzler et al, 2000) 用来实现 MOEA 中两解集相对覆盖率的比较。在该方法中,假设 P ′ ⊆ P P^{'} \subseteq P P′⊆P 和 P ′ ′ ⊆ P P^{''} \subseteq P P′′⊆P 是目标空间中两个解集( P P P 为 F k n o w n F_{known} Fknown 或 P F k n o w n PF_{known} PFknown),将 ( P ′ , P ′ ′ ) (P^{'},P^{''}) (P′,P′′) 映射到 [0, 1] 之间,则得 P ′ P^{'} P′ 和 P ′ ′ P^{''} P′′ 之间的覆盖率(tow set coverage, CS),计算公式为
C S ( P ′ , P ′ ′ ) ≜ ∣ { a ′ ′ ∈ P ′ ′ ∣ ∃ a ′ ∈ P ′ , a ′ ≻ a ′ ′ 或 a ′ = a ′ ′ } ∣ ∣ P ′ ′ ∣ CS(P^{'}, P^{''}) \triangleq \frac {| \{ a^{''} \in P^{''} | ~ \exists a^{'} \in P^{'},a^{'} \succ a^{''} 或~ a^{'} = a^{''} \} |}{| P^{''} |} CS(P′,P′′)≜∣P′′∣∣{a′′∈P′′∣ ∃a′∈P′,a′≻a′′或 a′=a′′}∣
\quad\quad 如果 P ′ P^{'} P′ 中所有的点都支配或等于 P ′ ′ P^{''} P′′ 中所有的点,那么可以定义 C S = 1 CS = 1 CS=1,反之 C S = 0 CS=0 CS=0。 一般来说,由于 P ′ P^{'} P′ 与 P ′ ′ P^{''} P′′ 这两个解集的交集并不为空,所以在评价一个 MOEA 时, C S ( P ′ , P ′ ′ ) CS(P^{'}, P^{''}) CS(P′,P′′) 与 C S ( P ′ ′ , P ′ ) CS(P^{''}, P^{'}) CS(P′′,P′) 必须同时考虑。这种评价方法的优点是计算简单,能够提供 MOEA 不同代之间在支配关系上的相对比较关系。同时也要注意这种方法并不是距离上的比较,而是解集上的比较,可以说是一种特殊的评价方法。
\quad\quad 3. 世代距离
\quad\quad Van Veldhuizen 与 Lamont 在 1998 年提出来一种评价方法世代距离 (generational distance, GD) (Veldhuizen et al, 1998),用来表示 P F k n o w n PF_{known} PFknown 与 P F t r u e PF_{true} PFtrue 之间间隔距离,其计算公式如下:
G D ≜ ( ∑ i = 1 n d i p ) 1 / p n GD \triangleq \frac {(\sum_{i=1}^n d ^p_i)^{1/p}}{n} GD≜n(∑i=1ndip)1/p
式中, n n n 是 P F k n o w n PF_{known} PFknown 中的向量个数, p = 2 p=2 p=2, d i d_i di 表示目标空间上每一维向量与 P F t r u e PF_{true} PFtrue 中最近向量之间的欧几里得距离。若结果为 0,则表示 P F t r u e = P F k n o w n PF_{true} = PF_{known} PFtrue=PFknown;而其他的值都表示 P F k n o w n PF_{known} PFknown 偏离 P F t r u e PF_{true} PFtrue 的程度。以图 10.1 为例,计算可得:
d
1
=
(
2.5
−
2
)
2
+
(
9
−
8
)
2
d_1 = \sqrt{(2.5 - 2)^2 + (9 - 8)^2}
d1=(2.5−2)2+(9−8)2
d
2
=
(
3
−
3
)
2
+
(
6
−
6
)
2
d_2 = \sqrt{(3 - 3)^2 + (6 - 6)^2}
d2=(3−3)2+(6−6)2
d
3
=
(
5
−
4
)
2
+
(
4
−
4
)
2
d_3 = \sqrt{(5 - 4)^2 + (4 - 4)^2}
d3=(5−4)2+(4−4)2
因此, P F k n o w n PF_{known} PFknown 与 P F t r u e PF_{true} PFtrue 之间间隔距离为 G D = 1.11 8 2 + 0 2 + 1 2 / 3 = 0.5 GD = \sqrt{1.118^2 +0^2 + 1^2}/3 = 0.5 GD=1.1182+02+12/3=0.5
\quad\quad Schott 于 1995 年提出了一种称为 “七点” 平均距离的评价方法(Schott, 1995),这与计算世代距离的思想是一样的。Schott 认为,在实际问题中, F t r u e F_{true} Ftrue 或 P F t r u e PF_{true} PFtrue 都是很难求得其准确值的,因此想直接釆用 F t r u e F_{true} Ftrue 或 P F t r u e PF_{true} PFtrue 的值来对 MOEA 进行评价是很难实现的,所以,他在目标空间生成七个点来代替 F t r u e F_{true} Ftrue 或 P F t r u e PF_{true} PFtrue 用于比较,这样可以提高评价方法的准确性。 假设针对一个 2 维的最小化多目标优化问题, f 1 f_1 f1 和 f 2 f_2 f2 是两个目标向量,且 ( f 1 f_1 f1, f 2 f_2 f2) 的起点是 (0, 0),首先计算岀每一维目标的最大值,然后在每一维原点到最大点之间选择两个点,这样就选出了七个点。通过计算七个点与 P F k n o w n PF_{known} PFknown 中最近向量之间的欧几里得距离的平均值,实现评价。假设一个 2 维最小化最优问题为 F ( x ) = ( f 1 ( x ) , f 2 ( x ) ) F(x) = (f_1(x), f_2(x)) F(x)=(f1(x),f2(x)),七个点可以这样选取:
{ ( 0 , ( m a x f 2 ( x ) ) / 3 ) , ( 0 , 2 ∗ ( m a x f 2 ( x ) ) / 3 ) , ( 0 , ( m a x f 2 ( x ) ) ) , ( 0 , 0 ) , ( ( m a x f 1 ( x ) ) / 3 , 0 ) , ( 2 ∗ ( m a x f 1 ( x ) ) / 3 , 0 ) , ( ( m a x f 1 ( x ) ) , 0 ) } \{(0, (maxf_2(x))/3), (0, 2 * (maxf_2(x))/3), (0, (maxf_2(x))), (0, 0), \\ ( (maxf_1(x))/3, 0), (2 * (maxf_1(x))/3, 0), ((maxf_1(x)), 0)\} {(0,(maxf2(x))/3),(0,2∗(maxf2(x))/3),(0,(maxf2(x))),(0,0),((maxf1(x))/3,0),(2∗(maxf1(x))/3,0),((maxf1(x)),0)}
\quad\quad 4. 最大出错率
\quad\quad 当对一个解集进行评价时,很难估计一个解集的一些向量优于其他解集的程度。例如,在比较 P F k n o w n PF_{known} PFknown 和 P F t r u e PF_{true} PFtrue,有的人希望同时比较两个解集的趋近程度以及两个解集的覆盖程度。这种比较特殊的评价要求考虑 P F k n o w n PF_{known} PFknown 在 P F t r u e PF_{true} PFtrue 中的每一维向量上的最大出错率(maximum pareto front error, ME) 。换句话说,就是要考虑 P F k n o w n PF_{known} PFknown 中的每一维向量与 P F t r u e PF_{true} PFtrue 中最近向量的最小距离的最大者。以 2 维为例,这种评价方法定义如下(Coello Coello et al, 2002):
M E ≜ max j ( min i ∣ f 1 i ( x ) − f 1 j ( x ) ∣ p + ∣ f 2 i ( x ) − f 2 j ( x ) ∣ p ) 1 / p ME \triangleq \max_j(\min_{i} |~ f_1^i(x) - f_1^j(x) ~|^p + |~ f_2^i(x) - f_2^j(x)~ |^p )^{1/p} ME≜jmax(imin∣ f1i(x)−f1j(x) ∣p+∣ f2i(x)−f2j(x) ∣p)1/p
式中, i i i 和 j j j 分别是 P F k n o w n PF_{known} PFknown 与 P F t r u e PF_{true} PFtrue 的向量标识, ( i = 1 , . . . , n 1 ) , ( j = 1 , . . . , n 2 ) , p = 2 。 (i=1, ..., n_1), (j=1, ..., n_2),p=2。 (i=1,...,n1),(j=1,...,n2),p=2。 若结果为 0,表明 P F k n o w n PF_{known} PFknown ⊆ P F t r u e \subseteq PF_{true} ⊆PFtrue 而其他的值则表示 P F k n o w n PF_{known} PFknown 中至少有一个向量不在 P F t r u e PF_{true} PFtrue 中。以图 10.1 为例,求得图中的 P F k n o w n PF_{known} PFknown 中的向量离 P F t r u e PF_{true} PFtrue 最近的分别是 1.118、0 和 1。 因此, M E = 1.118 ME = 1.118 ME=1.118。
\quad\quad 5. 高维空间及其比率
\quad\quad Zitzler 与 Thiele 在 1998 年提出了一种多目标进化算法的评价方法(Zitzler et al, 1998),称为高维空间(hyperarea)。高维空间是指在目标空间中被 P F k n o w n PF_{known} PFknown 所覆盖的那一部分空间 (或者称为曲线下空间)。例如,在一个 2 维优化问题中, P F k n o w n PF_{known} PFknown 中的一个向量定义了一个由原点与 ( f 1 ( 1 ) , f 2 ( x ) ) (f_1(1), f_2(x)) (f1(1),f2(x)) 所围成的矩形空间。这种由 P F k n o w n PF_{known} PFknown 中每一维向量所围成的矩形空间的集合就是该方法所说的高维空间,其定义如下:
H ≜ { ∪ i a i ∣ v i ∈ P F k n o w n } H \triangleq \{\underset{i}{\cup} a_i~|~ v_i \in PF_{known}\} H≜{i∪ai ∣ vi∈PFknown}
式中, v i v_i vi 是 P F k n o w n PF_{known} PFknown 中的非支配向量,而 a i a_i ai 就是由原点及 v i v_i vi 所形成的高维空间。以图 10.1 为例可知,由(0, 0)和 Pareto 面上的点(4, 4)所围成的矩形区域有 16 个单位的面积, 由(0, 0)及(3, 6)围成的矩形区域有 3 × ( 6 − 4 ) = 6 3 × (6 - 4) = 6 3×(6−4)=6 个单位的空间。所以, P F t r u e PF_{true} PFtrue 的 H = 16 + 6 + 4 + 3 = 29 H = 16 + 6 + 4 + 3 = 29 H=16+6+4+3=29 个单位,而 P F k n o w n PF_{known} PFknown 的 H = 20 + 6 + 7.5 = 33.5 H = 20 + 6 + 7. 5 = 33. 5 H=20+6+7.5=33.5 个单位。
\quad\quad 同时 Zitzler 与 Thiele 注意到,当 P F k n o w n PF_{known} PFknown 非凸时,这种评价方法存在着一些误差。并且在进行评价时,他们预先假设了 MOP 的原点是 ( 0 , ⋅ ⋅ ⋅ , 0 ) (0,···, 0) (0,⋅⋅⋅,0), 但是并不是所有的情况都是这样的。虽然 P F k n o w n PF_{known} PFknown 中的向量都能映射到以原点为中心的区域,但是不同的优化问题其每一维向量映射的范围是不同的,这样最优的 H H H 值的变化范围就会很大。为了解决这个问题,他们又对该方法进行改进,提出了高维空间比率(hgperarea ratio, HR),其定义如下:
H R ≜ H 1 H 2 HR \triangleq \frac{H_1}{H_2} HR≜H2H1
式中, H 1 H_1 H1 和 H 2 H_2 H2 分别是 P F k n o w n PF_{known} PFknown 与 P F t r u e PF_{true} PFtrue 的高维空间。在最小化问题中,该比率为 1 表示 P F k n o w n = P F t r u e PF_{known}=PF_{true} PFknown=PFtrue,大于 1 则表示 P F k n o w n PF_{known} PFknown 中覆盖的高维空间要大于 P F t r u e PF_{true} PFtrue 中的高维空间。以图 10.1 为例:
H R = 33.5 29 = 1.155 HR = \frac{33.5}{29} = 1.155 HR=2933.5=1.155
\quad\quad 6. 基于距离的趋近度评价方法
\quad\quad Deb 于 2002 年提出一种趋近度评价方法(Deb et al, 2002b)。该方法采用计算解集到参照集或 Pareto 最优解集的最小距离来衡量算法的趋近程度,距离越小,表示趋近程度越高。
\quad\quad 该方法在评价一个 MOEA 的收敛性时需要用到参考集 P ∗ P^* P∗ ,参考集 P ∗ P^* P∗ 要么是已知的 Pareto 最优解集,要么为历代非支配集并集的非支配集,即 P ∗ = N o n − d o m i n a t e d ( ∪ t = 0 T N d s ( t ) ) P^* = Non-dominated(\cup^T_{t=0}Nds^{(t)}) P∗=Non−dominated(∪t=0TNds(t)),其中, N d s ( t ) Nds^{(t)} Nds(t) 为第 t t t 代进化 P ( t ) P^{(t)} P(t) 所对应的非支配集, ( t = 0 , 1 , … , T ) (t=0, 1,…, T) (t=0,1,…,T)。 因为 MOP 的 Pareto 最优解集一般是很难得到的,所以参考集 P ∗ P^* P∗ 通常为历代非支配集并集的非支配集。
\quad\quad ① 计算当前非支配集中每个个体 i i i 到 P ∗ P^* P∗ 的最短欧几里得距离:
p d i = min j = 1 ∣ P ∗ ∣ ∑ k = 1 m ( f k ( i ) − f k ( j ) f k m a x − f k m i n ) 2 pd_i = \min_{j=1}^{|P^{*}|} \sqrt{\sum_{k=1}^{m} \left( \frac {f_k(i) - f_k(j)} {f_k^{max} - f_k^{min}} \right)^2} pdi=j=1min∣P∗∣k=1∑m(fkmax−fkminfk(i)−fk(j))2
式中, f k m a x f_k^{max} fkmax 和 f k m i n f_k^{min} fkmin 分别为参考集 P ∗ P^* P∗ 中第 k k k 个目标的最大和最小值, m m m 为子目标的数目。
\quad\quad
② 计算
p
d
i
pd_i
pdi 的平均值:
C
(
P
(
t
)
)
=
∑
i
=
1
∣
N
d
s
(
t
)
∣
p
d
i
/
∣
N
d
s
(
t
)
∣
C(P^{(t)}) = \sum_{i=1}^{|Nds^{(t)}|} pd_i / |Nds^{(t)}|
C(P(t))=i=1∑∣Nds(t)∣pdi/∣Nds(t)∣
\quad\quad 为满足 C ( P ( t ) ) ∈ [ 0 , 1 ] , C(P^{(t)}) \in [0,1], C(P(t))∈[0,1], 对式(10.9)做处理:
C ‾ ( P ( t ) ) = C ( P ( t ) ) / C ( P ( 0 ) ) (10.9) \overline{C}(P^{(t)}) = C(P^{(t)}) / C(P^{(0)}) \tag{10.9} C(P(t))=C(P(t))/C(P(0))(10.9)
C ( P ( t ) ) \quad\quad C(P^{(t)}) C(P(t)) 就是衡量 MOEA 所求的解集趋近程度的值,值越小,表明解集趋近于 Pareto 最优面的程度越高;反之,值越大,解集趋近于 Pareto 最优面的程度越低。 C ‾ ( P ( t ) ) \overline{C}(P^{(t)}) C(P(t)) 的值处于 0〜1 之间,当用于表达 MOEA 收敛速度时,其值越小,表明解集收敛越快,而其值越大,则表明解集收敛越慢。
\quad\quad
另外,对于一些特殊的测试问题,如 Deb 提岀的 DLTZ2 或 DLTZ3,其 Pareto 最优解集
P
F
t
r
u
e
PF_{true}
PFtrue 是已知的,因此可以计算趋近度值:
p
d
i
=
∣
∣
r
A
∣
∣
−
1
pd_i = ||r_A|| - 1
pdi=∣∣rA∣∣−1
式中, r A r_A rA 为 A ∈ N d s A \in Nds A∈Nds 到 P t r u e P_{true} Ptrue 的正交距离。
3.3 分布性评价方法
\quad\quad 在设计 MOEA 时,除了考虑算法的收敛性外,算法解集的多样性也是需要考虑的一个重要指标,即所得解集中的非支配个体应均匀分布在整个解空间中。对于解集分布性的评价,研究者普遍认为解集的分布度应当包括两个方面:解集分布的均匀程度和解集分布的广度。并且认为对于解集中被支配的个体,可以不考虑其分布情况,也就是说只考虑解集中的非支配个体。
\quad\quad 1999年,Zitzler 等提出一种基于小生境的分布性评价方法(Zitzler et al, 1999),这种方法要求设定一个小生境半径,通过计算每一个小生境半径范围内非支配解的个数来评价分布度。但由于小生境半径非常难以设定和调整,因此这种方法在实践中很少被采用。2000 年,Zitzler 等提出基于距离的评价方法(Zitzler et al, 2000),通过计算非支配集中每一个个体到其他个体的距离的平均值的方差来评价种群的分布度。方差值越小,种群的分布度越好,但是这种方法所得的值并不能反映解集的实际分布情况,特别是当目标数较多时(大于 3)。近年来,研究者们提出了很多种分布度评价方法,下面比较详细地讨论几种有代表性的方法,并分析其优缺点。
\quad\quad 1. 空间评价方法
\quad\quad 空间评价方法 (spacing metric) 是由 Deb 等于 2002 年提出的 (Deb et al, 2002b),用来评价近似解集中个体在目标空间的分布情况。
评价函数定义如下:
Δ = ∑ i = 1 ∣ P F ∣ d i − d ‾ ∣ P F ∣ \Delta = \sum_{i=1}^{|PF|} \frac{d_i - \overline d}{|PF|} Δ=i=1∑∣PF∣∣PF∣di−d
式中, P F PF PF 代表已知的 Pareto 最优面, d i d_i di 是指解集中非支配边界上两个连续向量的欧几里得距离, d ‾ \overline d d 是这些距离的平均值。值得说明的是,这种评价方法比较适用于 2 维目标空间, 而在高维目标情况 (特别当目标大于 3 时) 效果不理想。
\quad\quad 类似地,Schott 提岀了一种计算分布性的方法(Schott Jason, 1995),定义如下:
Δ
′
=
1
n
−
1
∑
i
=
1
n
(
d
‾
−
d
i
)
2
\Delta^{'} = \sqrt{ \frac{1}{n-1} \sum_{i=1}^{n} {(\overline d - d_i )^2}}
Δ′=n−11i=1∑n(d−di)2
d
i
=
m
i
n
j
(
∣
f
1
i
(
x
)
−
f
1
j
(
x
)
∣
+
∣
f
2
i
(
x
)
−
f
2
j
(
x
)
∣
)
,
(
i
,
j
=
1
,
2
,
⋅
⋅
⋅
,
n
)
d_i = min_j(| f_1^i(x) - f_1^j(x)| + | f_2^i(x) - f_2^j(x)|),(i, j = 1, 2, ···, n)
di=minj(∣f1i(x)−f1j(x)∣+∣f2i(x)−f2j(x)∣),(i,j=1,2,⋅⋅⋅,n)
\quad\quad 式中, d ‾ \overline d d 是所有 d i d_i di 的平均值, n n n 是已知的 Pareto 边界的大小。如果这种评价方法能和其他方法结合起来,它能提供所得解的分布信息,使得结果更为准确。与上一种方法不同的是, 这种方法能够适用于 2 维以上的 MOP,但这种方法计算复杂度较高。
\quad\quad 2. 基于信息熵的评价方法
\quad\quad Farhang-Mehr 在 2002年 提出了一种依靠个体信息的分布性评价方法 (Far hang-Mehr et al, 2002),它是采用个体的信息嫡来评价解集的分布情况。为便于讨论,下面先介绍影响函数和密度函数。
\quad\quad (1) 影响函数
\quad\quad 对一个 m m m 维 MOP,与人类社会一样,种群中的每两个个体必定会互相影响,困难的是如何来测量它们之间的影响程度。因此,人们定义了一个函数来描绘它,这个函数就称为影响函数 (influence function) 。在目标空间中,定义个体 i i i 对个体 y y y 的影响值为
ψ ( l i → y ) : R → R \psi (l_{i \to y}):R \to R ψ(li→y):R→R
\quad\quad 显然,影响函数是随着个体 i i i 到个体 y y y 的距离的增加而减小的,这样的函数有很多种, 例如抛物线、波浪线或高斯函数。高斯函数的定义为:
ψ ( r ) = ( 1 / ( σ 2 π ) ) e − r 2 / 2 σ 2 \psi (r) = (1/(\sigma \sqrt {2 \pi}))~ e^{-r^{2}/2\sigma^2} ψ(r)=(1/(σ2π)) e−r2/2σ2
式(10.14)中, σ \sigma σ 为分布度的标准方差。如果 σ \sigma σ 值很小,影响函数的变化就非常快,因此很可能距离很近的点之间的影响也不是很大,这样,个体的密度值就不能正确地反映其分布情况。相反, σ \sigma σ 值太大,使得影响函数变化平稳,密度值同样也不能反映个体分布,所以如何选取合适的 σ \sigma σ 值是非常重要的。
\quad\quad (2) 密度函数
\quad\quad 按照个体的空间距离得出影响函数之后,就可以得到每个个体的密度值。一个个体的密度值 (density) 是指目标空间中其他个体对它的影响函数值的总和。假设可行空间包含 N N N 个个体,点 y y y 是其中的一个个体,则个体 y y y 的密度值可表示为
D ( y ) = ∑ i = 1 N ψ ( l ( i , y ) ) D(y) = \sum_{i=1}^{N} \psi(l(i, y)) D(y)=i=1∑Nψ(l(i,y))
\quad\quad 在对一个算法进行评价时,首先将解集中的非支配个体映射到一个合适的超平面上,这样就可以考虑一维的信息,然后将映射平面分为若干个网格(或者是 m − 1 m - 1 m−1 维的盒子),计算网络中个体的密度值,然后根据 Shannon 函数计算个体信息熵值。
如当目标为 2 维时,将映射空间划分为 a 1 × a 2 a_1 × a_2 a1×a2 的网络,计算公式为:
ρ i j = D i j ∑ k 1 = 1 a 1 ∑ k 2 = 1 a 2 D k 1 k 2 \rho_{ij} = \frac{D_{ij}}{\sum_{k_1 = 1}^{a1}\sum_{k_2 = 1}^{a2} D_{k1k2}} ρij=∑k1=1a1∑k2=1a2Dk1k2Dij
显然:
∑ K 1 = 1 a 1 ∑ K 2 = 1 a 2 ρ k 1 k 2 = 1 ; ∀ k 1 , k 2 ρ k 1 k 2 ≥ 0 \sum_{K_1 =1}^{a_1} \sum_{K_2 =1}^{a_2} \rho_{k_1k_2} = 1;\forall k_1, k_2~~~~~~~ \rho_{k_1k_2} ≥ 0 K1=1∑a1K2=1∑a2ρk1k2=1;∀k1,k2 ρk1k2≥0
H = − ∑ K 1 = 1 a 1 ∑ K 2 = 1 a 2 ρ k 1 k 2 l n ( ρ k 1 k 2 ) H = -\sum_{K_1 =1}^{a_1} \sum_{K_2 =1}^{a_2} \rho_{k_1k_2} ~ ln(\rho_{k_1k_2}) H=−K1=1∑a1K2=1∑a2ρk1k2 ln(ρk1k2)
\quad\quad 一般的,对于 m m m 维的目标空间来说,可行空间被划分为 a 1 × a 2 × ⋅ ⋅ ⋅ × a n a_1 × a_2 × ··· × a_n a1×a2×⋅⋅⋅×an, 个体信息嫡值计算如下:
H = − ∑ K 1 = 1 a 1 ∑ K 2 = 1 a 2 ⋅ ⋅ ⋅ ∑ K m = 1 a m ρ k 1 k 2 ⋅ ⋅ ⋅ k m l n ( ρ k 1 k 2 ⋅ ⋅ ⋅ k m ) H = -\sum_{K_1 =1}^{a_1} \sum_{K_2 =1}^{a_2} ··· \sum_{K_m =1}^{a_m} \rho_{k_1k_2 ··· k_m} ~ ln(\rho_{k_1k_2 ··· k_m}) H=−K1=1∑a1K2=1∑a2⋅⋅⋅Km=1∑amρk1k2⋅⋅⋅km ln(ρk1k2⋅⋅⋅km)
\quad\quad 当解集的分布性越好时, H H H 的值越大;分布性越差时, H H H 的值越小
\quad\quad 这种方法存在的不足是:第一,信息嫡值在很大程度上取决于标准方差 σ \sigma σ 的选取;第二,对于 Pareto 最优面不连续的情况,该方法不适用。
\quad\quad 3. 网格分布度评价方法
\quad\quad Deb 于 2002 年提出了网格分布性评价方法(Debet al, 2002b),其方法是首先将解集中的非支配个体映射到一个合适的超平面上,这样就可以少考虑一维的信息,然后将映射平面分成一些网格(或者是 m − 1 m -1 m−1 维的盒子),根据格子里包含的非支配个体的情况来计算分布度函数。如果所有的格子都有非支配个体,那么这是分布最好的情况。如果有些网格没有 一个非支配个体,那么其分布性就比较差。这种方法需要选择一些参数,如映射的超平面、 网格的大小等。
\quad\quad 具体过程如下。
\quad\quad ① 从种群 p ( t ) p^{(t)} p(t) 中选出非支配集 F ( t ) F^{(t)} F(t), F ( t ) F^{(t)} F(t) 对 P ∗ P^* P∗ 是非支配的。
\quad\quad ② 对于每个网格 ( i , j , ⋅ ⋅ ⋅ ) (i, j, ···) (i,j,⋅⋅⋅),通过下面两个等式计算 H ( i , j , ⋅ ⋅ ⋅ ) H(i, j, ···) H(i,j,⋅⋅⋅); 和 h ( i , j , ⋅ ⋅ ⋅ ) h(i, j, ···) h(i,j,⋅⋅⋅):
H ( i , j , ⋅ ⋅ ⋅ ) = { 1 , 若在对应网络中有一个代表个体 X ( X ∈ p ∗ ) 0 , 其他 H(i, j, ···) = \begin{cases} 1, & \text{若在对应网络中有一个代表个体 $X(X \in p^*)$} \\ 0, & \text{其他} \\ \end{cases} H(i,j,⋅⋅⋅)={1,0,若在对应网络中有一个代表个体 X(X∈p∗)其他
h ( i , j , ⋅ ⋅ ⋅ ) = { 1 , 若 H ( i , j , ⋅ ⋅ ⋅ ) = 1 且在对应网络中有一个代表个体 X ( X ∈ F ( t ) 0 , 其他 h(i, j, ···) = \begin{cases} 1, & \text{若 $H(i, j, ···) = 1$ 且在对应网络中有一个代表个体 $X(X \in F^{(t)}$} \\ 0, & \text{其他} \\ \end{cases} h(i,j,⋅⋅⋅)={1,0,若 H(i,j,⋅⋅⋅)=1 且在对应网络中有一个代表个体 X(X∈F(t)其他
\quad\quad ③ 对于每个网格,根据 h ( i , j , ⋅ ⋅ ⋅ ) h(i, j, ···) h(i,j,⋅⋅⋅) 和与它相邻的 h ( ) h() h() 值计算 m ( h ( i , j , ⋅ ⋅ ⋅ ) ) m(h(i, j, ···)) m(h(i,j,⋅⋅⋅)) 的值。同样地,根据参照集中 H ( ) H() H() 的值计算 m ( H ( i , j , ⋅ ⋅ ⋅ ) ) m(H(i, j, ···)) m(H(i,j,⋅⋅⋅))
\quad\quad ④ 通过 m ( h ( i , j , ⋅ ⋅ ⋅ ) ) m(h(i, j, ···)) m(h(i,j,⋅⋅⋅)) 和 m ( H ( i , j , ⋅ ⋅ ⋅ ) ) m(H(i, j, ···)) m(H(i,j,⋅⋅⋅)) 的平均值计算分布性函数:
D ( P ( t ) ) = ∑ ( i , j , ⋅ ⋅ ⋅ ) ( H ( i , j , ⋅ ⋅ ⋅ ) ≠ 0 ) m ( h ( i , j , ⋅ ⋅ ⋅ ) ) ∑ ( i , j , ⋅ ⋅ ⋅ ) ( H ( i , j , ⋅ ⋅ ⋅ ) ≠ 0 ) m ( H ( i , j , ⋅ ⋅ ⋅ ) ) D(P^{(t)}) = \frac{\sum_{(i, j, ···) (H(i, j, ···)≠ 0)} m(h(i, j, ···))}{\sum_{(i, j, ···) (H(i, j, ···)≠ 0)} m(H(i, j, ···))} D(P(t))=∑(i,j,⋅⋅⋅)(H(i,j,⋅⋅⋅)=0)m(H(i,j,⋅⋅⋅))∑(i,j,⋅⋅⋅)(H(i,j,⋅⋅⋅)=0)m(h(i,j,⋅⋅⋅))
\quad\quad 简单地说,网格的函数 m ( ) m() m() 是通过该网格的 h ( ) h() h() 值和与之相邻的两个网格的 h ( ) h() h() 值求得的。连续 3 个 h ( ) h() h() 组成的一组总共有 8 种可能,应该注意:
\quad\quad ① 在这些情况中,111 应当是分布最好的情况,000 则是最差情况。
\quad\quad ② 010 或 101 表示有较好分布的周期性的情况,它们的值应当比 110 或 011 的值更大些。例如,1010101010 和 1111100000 这两种情况都覆盖了 50% 的网格,但显然 1010101010 的分布度要比 1111100000好。
\quad\quad ③ 110 或 011 的值要比 001 或 100 的值要大,因为前者覆盖的网格要多些。
\quad\quad 基于上面的讨论, m ( ) m() m() 和 h ( ) h() h() 的值可以进行如表 10.1 所示的定义。

\quad\quad 同样,H()的取值也和上表一样。显然这只是 2 维的取值情况,如果函数的目标数越多,表 10.1 的函数值就越难定义。
\quad\quad 图 10.2 是一个 2 维计算分布度的例子,为了避免边界的影响(如图 10.2 中使用假定的网格的影响),一般采用下面的公式计算:
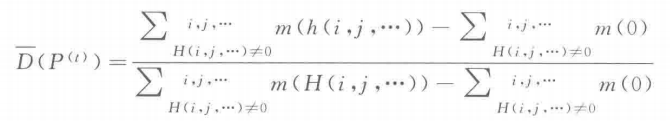
式中, m ( 0 ) m(0) m(0) 中的 0 是一个赋值为 0 的数组。
\quad\quad 如果 Pareto 最优边界不是已知的,目标集 P ∗ P^* P∗ 定义如下:
P ∗ = n o n − d o m i n a t e d ( ∪ t = 0 T N d s ( t ) ) , ( t = 0 , 1 , ⋅ ⋅ ⋅ , T ) P^* = non-dominated(\cup_{t=0}^T Nds^{(t)}),(t = 0, 1, ···, T) P∗=non−dominated(∪t=0TNds(t)),(t=0,1,⋅⋅⋅,T)
式中, T T T 为 MOEA 运行代数, N d s ( t ) Nds^{(t)} Nds(t) 为第 t t t 代进化种群 P ( t ) P^{(t)} P(t) 所对应的非支配集。
\quad\quad 在计算高维(目标数超过 2)时,釆用的是将所得解集的最后一维作为映射面,只考虑 了其他 n − 1 n-1 n−1 维的分布信息,即将 f n = 0 f_n=0 fn=0 这个平面作为映射面。
这种方法在目标数为 2 时,是非常准确的,但是当目标数比较多时,由于映射方法太简 单,丢失了一维的信息,使得计算出来的分布度值与实际情况并不完全相符。
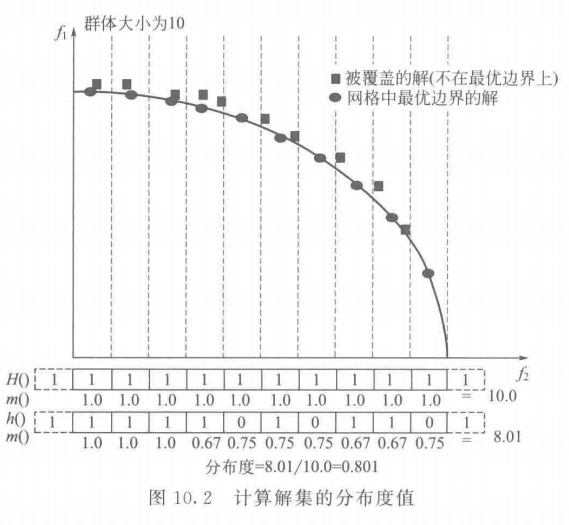
\quad\quad 4. 个体空间的分布性评价方法
\quad\quad Deb 于 2003 年提出了一种基于个体空间的分布性评价方法(sparsity measure) (Deb et al, 2003)。将求得的 Pareto 最优解通过一个标准化的单位向量 η \eta η 映射到一个适当的超平面 上,如图 10.3 所示,每个个体在超平面上均有一个映射,以映射点为中心形成一个边长大小为 d d d 的超盒,所有超盒覆盖的总空间大小被用来评价解集的分布性。如果解集中有许多聚集在一起的个体,则它们的映射后对应的超盒会互相重叠,所获得的分布度的评价值会较小。反之,如果解集分布得很好,那么其个体映射后对应的超盒所覆盖的空间就越大,分布度评价值也越大。显然,当超盒覆盖所有空间时,分布度达到最大值 1.000。图 10.3 中, “X” 表示个体,个体周围的方框表示个体映射后对应的超盒所覆盖的区域。
\quad\quad 在这种方法中,参数 d d d 是很重要的。选取的 d d d 太小,解集中个体之间的距离就有可能都比 d d d 大,这样会让所有算法求岀的解集都有 1.000 的分布度值。相反, d d d 值太大的话,就会使所有的解集的分布度值很小。那么如何得到参数 d d d 的值呢,在该方法中,参数 d d d 选择按以下方法求得:首先选取需要比较的算法所得出的最终解集,然后对每个解集计算它们的 个体之间的最小距离,选取其中值最大者作为参数 d d d 的值。实验证明,这样选取的参数 d d d 是比较合适的。
\quad\quad 然而,这种方法存在的不足如下:
\quad\quad ① 算法的时间复杂度较高,因此在进行分布度评价时往往只计算最后一代的分布度值, 这样一来,就不能对 MOEA 的进化过程进行分析。
\quad\quad ② 在计算个体空间时,遇到个体之间覆盖的空间重叠时,计算时会比较困难,且计算复杂度较高。
\quad\quad 5. 分布度逐步评价方法
\quad\quad 李密青等提出了分布度逐步评价方法(李密青等,2008), 该方法定义了一种基于角度的坐标,避免了算法因收敛性不同对分布性评价的影响。利用解集均匀分布具有的对称性, 把整个目标空间从大到小划分成不同的对称区域,逐步进行分布度评价。
\quad\quad (1)定义角度坐标
\quad\quad 首先定义一种基于个体角度的坐标,这种坐标只考虑个体的角度分量.不考虑个体之间 的距离,这样避免了算法因收敛性不同而对分布性评价造成的影响,坐标定义如下。
\quad\quad 当目标为 2 维时,坐标向量定义为
α = ( a r c s i n f 2 f 1 2 + f 2 2 ) \alpha = \left( arcsin \frac {f_2}{\sqrt{f_1^2 + f_2^2}} \right) α=(arcsinf12+f22f2)
\quad\quad 当目标为 3 维时,坐标向量定义为
α = ( a r c s i n f 2 f 1 2 + f 2 2 , a r c s i n f 3 f 2 2 + f 3 2 , a r c s i n f 1 f 3 2 + f 1 2 ) \alpha = \left( arcsin \frac {f_2}{\sqrt{f_1^2 + f_2^2}} , arcsin \frac {f_3}{\sqrt{f_2^2 + f_3^2}}, arcsin \frac {f_1}{\sqrt{f_3^2 + f_1^2}} \right) α=(arcsinf12+f22f2,arcsinf22+f32f3,arcsinf32+f12f1)
\quad\quad m 维目标空间的个体坐标 α \alpha α 是 C M 2 C_M^2 CM2 维向量,定义为
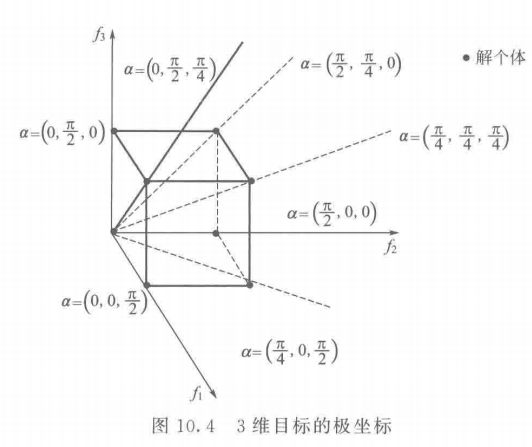
α = ( a r c s i n f 2 f 1 2 + f 2 2 , a r c s i n f 3 f 2 2 + f 3 2 , ⋅ ⋅ ⋅ , a r c s i n f M f M − 1 2 + f M 2 , a r c s i n f 1 f M 2 + f 1 2 , a r c s i n f 3 f 1 2 + f 3 2 , ⋅ ⋅ ⋅ ) \alpha = \left( arcsin \frac {f_2}{\sqrt{f_1^2 + f_2^2}} , arcsin \frac {f_3}{\sqrt{f_2^2 + f_3^2}}, ···, arcsin \frac {f_M}{\sqrt{f_{M-1}^2 + f_M^2}}, arcsin \frac {f_1}{\sqrt{f_{M}^2 + f_1^2}}, arcsin \frac {f_3}{\sqrt{f_1^2 + f_3^2}}, ···\right) α= arcsinf12+f22f2,arcsinf22+f32f3,⋅⋅⋅,arcsinfM−12+fM2fM,arcsinfM2+f12f1,arcsinf12+f32f3,⋅⋅⋅
\quad\quad 按以上定义确定的 3 维目标的极坐标如图 10.4 所示。
\quad\quad (2) 坐标变换
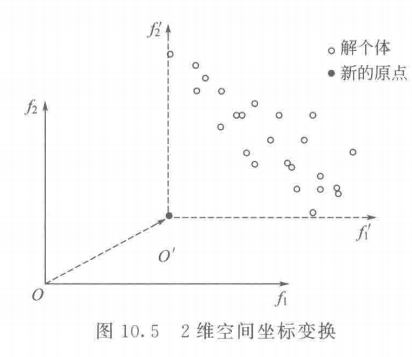
\quad\quad 一般地,测试问题的解个体并不能覆盖整个目标空间,为能在目标空间中准确地评价分布情况,需要对其进行变换。首先求出解群体中 各个目标上的最小值,然后以这些最小值组成的向量作为新原点,坐标变换过程如图 10.5 所示。
\quad\quad 原点 O ′ O' O′ 是由 f 1 f_1 f1 和 f 2 f_2 f2 上最小的值确定,根据点 O ′ O' O′ 形成了新的坐标轴 f 1 ′ f_1^{'} f1′ 和 f 2 ′ f_2^{'} f2′,这样经过坐标 变换的解个体就覆盖了整个目标空间。
\quad\quad (3) 分布度逐步评价方法
\quad\quad 分布度逐步评价方法利用了均匀分布的解集具有的对称性,先把整个目标空间 A 划分成两个对称区域 A 1 A_1 A1 和 A 2 A_2 A2,统计这两个区域的个体数目, 由数目的多少得出两个区域整体的分布关系,然后对区域 A 1 A_1 A1 和 A 2 A_2 A2 重复以上操作得到一些更小的区域 A 11 , A 12 , A 21 , A 22 A_{11}, A_{12}, A_{21}, A_{22} A11,A12,A21,A22 ,如此进行下去,直到每个区域只有一个个体或者区域大小已经足够小。具体过程如算法 10.1 所示。

\quad\quad 最终解集的分布度为 final _ diversity = all _ rank/all _ area,其中,all _ rank 为分布情况,all _ area 为总分布区域。
\quad\quad 实验结果表明,该方法能精确地评价解集的分布情况。但是在处理高维问题时,计算开销大。另外,该方法不适用于真实 Pareto 面不对称的非连续问题。
\quad\quad 6. 解集分布广度评价指标
\quad\quad MOEA 性能评价中,除了关注解集与 Pareto 最优面的逼近程度(收敛性)和解集在目标空间的分布的均匀程度(分布均匀性)外,解集在目标空间分布的广泛程度(分布广泛性)也是评价 MOEA 的重要指标。李密青等提出了一种独立评价解集分布广度的评价方法 (spread indicator, SI)(李密青等,2011)。
\quad\quad 不同于考虑极端个体的评价方法,该方法利用边界解集对非支配集分布范围进行评价, 通过对非支配集中边界解的性质和特点的分析,讨论了边界解与极端解之间的联系和区别, 并根据边界解级数区分不同边界解对分布范围的影响,进而利用低维空间超立方体进行分布范围的估计。同时,引入了与质心超体积的比较关系,避免了 MOEA 因收敛度不同对分布 广度评价结果的影响。
\quad\quad 首先确定解集中能准确反映其分布范围的个体集,即边界解集,定义如下。
\quad\quad 定义 10.1(超出关系) \quad ∀ p , q ∈ N D S , N D S \forall p, q \in NDS, NDS ∀p,q∈NDS,NDS 为 r r r 个目标的非支配集,若对其中的 m m m 个目标(不失一般性记为 f 1 ( X ) , f 2 ( X ) , ⋅ ⋅ ⋅ , f m ( X ) ( m ≤ r ) f_1(X), f_2(X), ···, f_m(X)(m ≤ r) f1(X),f2(X),⋅⋅⋅,fm(X)(m≤r),有 f k ( p ) ≥ f k ( q ) ( k = 1 , 2 , ⋅ ⋅ ⋅ , m ) f_k(p) ≥ f_k(q)(k = 1, 2, ···, m) fk(p)≥fk(q)(k=1,2,⋅⋅⋅,m) 并且 ∃ l ∈ { 1 , 2 , ⋅ ⋅ ⋅ , m } , f t ( p ) > f l ( q ) \exists l \in \{1, 2, ···, m\},f_t(p) > f_l(q) ∃l∈{1,2,⋅⋅⋅,m},ft(p)>fl(q) ,则称 p p p 在 f 1 ( X ) , f 2 ( X ) , ⋅ ⋅ ⋅ , f m ( X ) f_1(X), f_2(X), ···, f_m(X) f1(X),f2(X),⋅⋅⋅,fm(X) 中超出 q q q.
\quad\quad 定义 10.2 (边界解和边界解集) \quad 设有 r r r 个优化目标的非支配集 N D S NDS NDS,对 p ∈ N D S p \in NDS p∈NDS, 若存在 r − 1 r-1 r−1 个目标的目标集 F r − 1 ( X ) = ( f 1 ( X ) , f 2 ( X ) , ⋅ ⋅ ⋅ , f r ( X ) ) ∈ Ψ r , ∄ q ∈ N D S F_{r-1}(X) = (f_1(X), f_2(X), ···, f_r(X)) \in \Psi_r,\not \exists q \in NDS Fr−1(X)=(f1(X),f2(X),⋅⋅⋅,fr(X))∈Ψr,∃q∈NDS 在 F r − 1 ( X ) F_{r-1}(X) Fr−1(X) 上超岀 p p p, 则称 p p p 为非支配集 N D S NDS NDS 的边界解, N D S NDS NDS 中边界解构成的子集称为 N D S NDS NDS 的边界解集(boundary set, BS),即 B S = { p ∣ p ∈ N D S , ∃ F r − 1 ( X ) ∈ Ψ r , ∄ q ∈ N D S 在 F r − 1 ( X ) 上超出 p } BS = \{p ~| ~p \in NDS, \exists F_{r-1}(X) \in \Psi_r, \not \exists q \in NDS ~~在 ~~F_{r-1}(X) ~~上超出~~ p\} BS={p ∣ p∈NDS,∃Fr−1(X)∈Ψr,∃q∈NDS 在 Fr−1(X) 上超出 p} 。其中, Ψ r \Psi_r Ψr 为由其中任意目标构成的目标集的非空集合。
\quad\quad 对于 r r r 个优化目标的非支配集 N D S NDS NDS,若 ∣ N D S ∣ ≥ r |NDS| ≥ r ∣NDS∣≥r, 则 N D S NDS NDS 中至少存在 r r r 个边界解 (李密青 等2011)。
\quad\quad 确定边界集后,需要区分边界解集中不同个体对分布范围的不同影响,为此,需要给出边界解级数的概念。
\quad\quad 定义 10.3 (边界解级数) \quad 若边界解仅满足一个 r − 1 r-1 r−1 维目标集,称为一级边界解;若满足 m m m 个 r − 1 r-1 r−1 维目标集,则称为 m m m 级边界解。
\quad\quad 级数不同的边界解集对分布范围的影响不同,边界解满足的目标集数目越多对解集分布范围的影响越大。将满足所有 r − 1 r-1 r−1 维目标集的边界解称为完全边界解。
\quad\quad 最后,根据边界解的定义设计一种评价边界解集的方法,该方法能反映不同个体对分布范围的影响程度。
\quad\quad 由于空间中解集分布的范围很难测定,不同问题的解集有着不同形状的分布。因此, I S IS IS 利用超立方体对不同形状的解集进行分布广度估计.具体过程如算法 10.2 所示。

\quad\quad 算法 10.2 通过计算在低一维目标集中边界解集与参考点的超体积来估计非支配集分布的广泛程度, V V V 值越大表明非支配集分布得越广泛。由于边界解评价次数与级数相对应,因此级数大的边界解将更多地影响着最终评价结果。在步骤 4 中,采用 hypervolume 来估计边界解集分布广度。在步骤 3 参考点的选择中,用超棱锥来模拟非支配集形状, 然而由于非支配集通常为曲面分布,因此决定参考点的单位距离通常会略大于非支配集中邻近个体的平均距离,但正是这种“略远”的参考点将有利于 hypervolume 的正确评价。在实验中发现, hypervolume 的计算结果受解集收敛性的影响,收敛性差的解集有着更大 hypervolume 值。对此,引入了计算质心与参考点围成的超体积。由于同一非支配集中的个体通常拥有相同的收敛度,因此对于拥有分布性相同,但收敛性不同的非支配集, 由边界解集和参考点围成的超体积与由质心和参考点围成的超体积之比为基本恒定的值, 这样就很好地避免了收敛性差异对分布广度评价结果造成的影响。图 10.6 为算法 10.2 的一个直观示例。图 10.6 (a) 中浅色圆点为非支配集 N D S NDS NDS 中个体,黑色圆点为 N D S NDS NDS 中个体在 f 3 ( X ) = 0 f_3(X)=0 f3(X)=0 上的映射,即 N D S 3 NDS_3 NDS3;图 10.6 (b) 中三角形为 KaTeX parse error: Expected group after '_' at position 4: NDS_̲ 中边界解集 B S 3 ′ BS_3^{'} BS3′ ,空心圆点为 N D S 3 NDS_3 NDS3 中非边界解集,即 N D S 3 − B S 3 ′ NDS_3-BS_3^{'} NDS3−BS3′,实心圆点为参考点 r e f 3 ref_3 ref3,五角星为 N D S 3 NDS_3 NDS3 的质心 c c c。 则它们在 f 1 − f 2 f_1 - f_2 f1−f2 平面上的评价结果为 B S 3 ′ BS_3^{'} BS3′ 和 r e f 3 ref_3 ref3 围成的面积与 c c c 和 r e f 3 ref_3 ref3 围成的面积之比。

\quad\quad 通过实验验证, S I SI SI 在解集分布广度上的评价是非常有效的,但是由于 S I SI SI 引入质心消除了收敛性的影响,因此在评价质心相对位置差异较大的非均匀问题的分布广度时可能会存在偏差。另外, S I SI SI 的评价指标是基于 hypervolume 的,它也具有所有基于 hypervolume 的评价方法的共同缺点,即对参考点敏感,并具有较高的时间复杂度。
4. 综合评价指标
\quad\quad 综合评价指标通过一个标量值来同时反映 MOEA 的收敛性和分布性。近年来被广泛运用的综合评价指标有超体积评价指标 (hypervolume, HV) (Zitzler et al, 1999) 和反转世代距离评价指标 (inverted generational distance, IGD) (Czyzzak et al, 1998) 。
4.1 超体积指标
\quad\quad
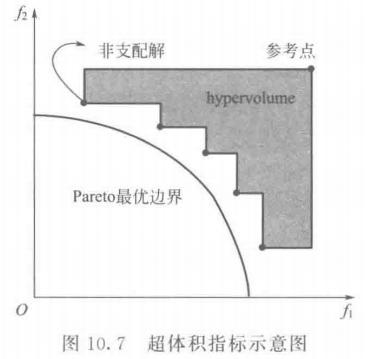
超体积指标因为其良好的理论支撑,已成为比较流行的评价指标。通过计算非支配解集与参考点围成的空间的超体积的值实现对 MOEA 综合性能的评价。如图 10.7 所示,对于 2 维问题来说,非支配解集与参考点构成的区域为灰色阴影部分。这里,参考点的设置有两种:最差点(非支配解集每维上的最大值组成的向量)和松散形式的最差点(Debet al, 2010) 。计算公式为
H
V
=
λ
(
∪
i
=
1
∣
S
∣
v
i
)
HV = \lambda(\cup_{i=1}^{|S|} v_i)
HV=λ(∪i=1∣S∣vi)
式中, λ \lambda λ 代表勒贝格测度, v i v_i vi 代表参考点和非支配个体 p i p_i pi 构成的超体积,S代表非支配集。
\quad\quad 超体积指标值是严格遵守 Pareto 支配原则的,以最小化问题为例,如果个体 A 支配个体 B,则个体 A 的超体积指标值一定大于个体 B 的超体积指标值,该结论推广到两个解集之间的支配关系,也是成立的。同时,因为超体积指标的计算过程不需要知道 Pareto 最优面,所以具有很好的实用性。但是,超体积指标还有两个缺陷:第一,超体积指标的计算时间非常大;第二,参考点的选择在一定程度上决定超体积指标值的准确性。
源码实现
4.2 反转世代距离
\quad\quad 在 3.2 节收敛性评价方法中对世代距离评价指标进行了详细的介绍。世代距离是指算法所求得的非支配解集 P F k n o w n PF_{known} PFknown 中所有个体到 Pareto 最优解集 P F t r u e PF_{true} PFtrue 的平均距离。而反转世代距离则是世代距离的逆向映射,它采用 Pareto 最优解集 P F t r u e PF_{true} PFtrue 中的个体到算法所求得的非支配解集 P F k n o w n PF_{known} PFknown 的平均距离表示 (Czyzzak et al, 1998)。因此,其计算公式为
I G D = ∑ j ‾ ∈ P F ∗ d j ‾ ′ n IGD = \frac{\sum_{\overline{j} \in PF^*} d^{'}_{\overline{j}}}{n} IGD=n∑j∈PF∗dj′
其中, d j ‾ ′ = m i n i ‾ ∈ P ∣ j ‾ − i ‾ ∣ d^{'}_{\overline{j}} = min_{\overline{i}\in P} |\overline{j} - \overline{i}| dj′=mini∈P∣j−i∣ 表示 Pareto 最优面上的点 j ‾ \overline{j} j 到最终解集 P P P 中个体 i ‾ \overline{i} i 的最小欧几里得距离。IGD 值越小,就意味着算法的综合性能越好。
\quad\quad 另外,为了更直观地体现 IGD 指标对解集综合性能的评价,分别给出了用 GD 和 IGD 指标评价解集 S S S 的性能的示意图,如图 10.8 所示。在解集 S S S 中包含 5 个非支配解,如图 10.8 (a) 所 示,它们非常接近 Pareto 最优解集,因此通过 G D GD GD 计算公式可以发现,它的收敛性较好。同时可以观察到该解集的分布性能不好,通过 10.8 (b) 计算得到的 IGD 值相对比较大。如果解集收敛好且分布均匀广泛,则计算得到的 IGD 值必然很小。因此可以说明 IGD 指标除了能反映 MOEA 的收敛性外,还能很好地反映 MOEA 的分布均匀性和广泛性。

源码实现
function Score = IGD(PFKnown,PFTrue)
% <metric> <min>
% Inverted generational distance
%------------------------------- Reference --------------------------------
% C. A. Coello Coello and N. C. Cortes, Solving multiobjective optimization
% problems using an artificial immune system, Genetic Programming and
% Evolvable Machines, 2005, 6(2): 163-190.
%------------------------------- Copyright --------------------------------
% Copyright (c) 2018-2019 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------
% 通过 pdist 计算 PFTrue 与 PFKnown 两两欧式距离,通过 min 取每一行的最小值作为列向量
% 最后再取所有距离的平均值,越小说明分布性和收敛性越好
Distance = min(pdist2(PFTrue,PFKnown),[],2);
Score = mean(Distance);
end





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








