基于遗传编程的符号回归（gplearn 介绍）

0 前言

作为一种监督学习方法，符号回归（symbolic regression）试图发现某种隐藏的数学公式，以此利用特征变量预测目标变量。

符号回归的具体实现方式是遗传算法（genetic algorithm）。一开始，一群未经历选择的公式会被随机生成。此后的每一代中，最「合适」的公式们将被选中。随着迭代次数的增长，不断繁殖、变异、进化，从而不断逼近数据分布的真相。

Gitee 源码： https://gitee.com/futurelqh/symbolic-regression/tree/master/gplearn

gplearn包括了一系列不同的函数，以供用户选择。它们的关键词是：

• ‘add’：加法，二元运算
• ‘sub’：减法，二元运算
• ‘mul’：乘法，二元运算
• ‘div’：除法，二元运算
• ‘sqrt’：平方根，一元运算
• ‘log’：对数，一元运算
• ‘abs’：绝对值，一元运算
• ‘neg’：相反数，一元运算
• ‘inv’：倒数，一元运算
• ‘max’：最大值，二元运算
• ‘min’：最小值，二元运算
• ‘sin’：正弦（弧度），一元运算
• ‘cos’：余弦（弧度），一元运算

函数表示方法（Representation）

假设有两个特征 $X_0$ 和 $X_1$，需要预测目标 $y$。一个可能随机产生的公式是：

$$y=X_0^2-3\times X_1+0.5$$

也可以写作：

$$y=X_0\times X_0-3\times X_1+0.5$$

同时，把它转化成一个 S-表达式：
$$y=(+(-(\times X_0{X}_0)(\times 3X_1))0.5)$$

把这个公式表示成一棵语法树，其中函数是内部节点，用深蓝色表示，而变量和常量构成叶节点，用浅蓝色表示。

对于 GP 来说很重要的一点是，公式中的例如 $X_0\times X_0$ 子表达式，或者树中的任意子树，都能够被任意有效的表达所替换

事实上，在程序中，需要进一步简化 S-表达式 并且去掉所有的括号：
$$y=+-\times X_0{X}_0\times 3X_{1}0.5$$

有了上述这个表达式，就可以递归的实现这棵二叉树，底层主要是利用栈实现。（Python 中可以利用列表实现）

个体评价：适应度（Fitness）

和其他机器学习算法一样，遗传算法的核心在于衡量公式的适应度（fitness function）。在符号回归里，适应度的地位类似于目标函数、score、loss 和 error。

gplearn 的主要组成部分有两个：SymbolicRegressor 和 SymbolicTransformer。两者的适应度有所不同。

SymbolicRegressor 是回归器。它利用遗传算法得到的公式，直接预测目标变量的值。

SymbolicTransformer是转换器。它并不直接预测目标变量，而是转化原有的特征、输出新的特征，这在特征工程的阶段尤为有效。

SymbolicRegressor的适应度有三种，都是机器学习里常见的 error function：

• mae: mean absolute error
• mse: mean squared error
• rmse: root mean squared error

gplearn中的评价标准通过metric参数设置，对于SymbolicRegressor包括mse，rmse，对于SymbolicTransformer包括pearson，spearman，对于SymbolicClassifier包括log loss等。如果有自定义的适应度可以通过fitness.make_fitness()实现，比如想要使用MAPE (mean absolute percentage error)误差

def _mape(y, y_pred, w):
    """Calculate the mean absolute percentage error."""
    diffs = np.abs(np.divide((np.maximum(0.001, y) - np.maximum(0.001, y_pred)),
                             np.maximum(0.001, y)))
    return 100. * np.average(diffs, weights=w)
    
mape = make_fitness(function=_mape, greater_is_better=False)
est = SymbolicRegressor(metric=mape, verbose=1)

SymbolicTransformer 会最大化输出的新特征与目标变量之间的相关系数的绝对值：（并非相关系数本身，因为很大的负相关反而有利于预测）

• pearson：皮尔逊积矩相关系数（Pearson product-moment correlation coefficient），默认设置。因为它衡量线性相关度，所以适用于下一个预测器（分类或回归）是线性模型的情况。
• spearman：斯皮尔曼等级相关系数（Spearman’s rank correlation coefficient）。因为它衡量单调相关度，所以适用于下一个预测器（分类或回归）是决策树类模型的情况。

当然，用户也可以自定义适应度的标准。

遗传算法内，耗时最大的部分无疑是适应度的计算。所以，gplearn允许用户通过修改n_jobs参数控制并行运算。在数据量和公式数量较大时，并行计算的速度优势最为明显。

特殊情况限制

因为输入值很可能是随机产生的，所以这些函数需要处理诸如「除以零」的问题。因此，gplearn 中的许多函数并不符合它们原本的数学定义，而是「受保护」的修改版：

• 除法的分布在 -0.001 到 0.001 之间，则返回 1
• 平方根下的式子取绝对值 $\sqrt{|a|}$
• log 的参数也取绝对值 $lo{g}_a|b|$，或者当参数小于 0.001，直接返回 1
• 如果一个数在 -0.001 到 0.001 之间，则它的倒数返回零。

对目标变量进行标准化（standardization）和区间缩放（min-max-scaling）可以有效避免常数值区间不符的问题。

个体初始化（Initialization）

当执行一个遗传编程算法的实时，第一代并不知道需要最大化那一种表达式，通常是随机任意的将变量和函数进行混合，这样普遍会得到比较差的效果，这个时候可以通过人为的提供一个较好的初始化参数来初始化种群，从而增加算法性能，其中最重要的一个影响因素是，数据集的特征数量。

第一个要注重的参数是初始化数的深度 init_depth ，init_depth 是一个表示范围的整数二元组，第一代的深度，在这个范围内随机产生。默认 2-6 的范围通常是一个很好的起点，但是如果数据集有很多特征，可以把这个范围扩大，深度加深。

接下来要考虑的参数为种群的大小，如果特征比较少，并且函数集比较少，可以初始化一个较小的种群，相反，初始化一个交大的种群。

最后，需要决定出适合数据集的方法 init_method，'grow', 'full', or 'half and half' 中的一个

• grow： 公式树从根节点开始生长。在每一个子节点，gplearn 会从所有常数、变量和函数中随机选取一个元素。如果它是常数或者变量，那么这个节点会停止生长，成为一个叶节点。如果它是函数，那么它的两个子节点将继续生长。用 grow 策略生长得到的公式树往往不对称，而且普遍会比用户设置的最大深度浅一些
• full： 从函数集中选择作为内部节点，直到达到最大深度，然后再选择从常数或者变量中选择叶节点。倾向于生长对称的满树。
• half and half： 一般的种群执行 ‘grow’ 方法，另一半的种群执行 ‘full’

个体选择（Selection）

现在需要决定哪些种群将被进化到下一代。在 gplearn 中，是通过锦标赛完成的。从群体中随机选择一个较小的子集进行竞争，其规模由 tournament_size 参数控制。然后在这个子集中选择适应的最好的公式进入下一代。

锦标赛中，当设置一个较大的 tournament_size ，通常会更快地找到更合适的公式，进化过程将倾向于在更短的时间内收敛到一个解决方案。较小的 tournament_size 可能会在群体中保持更多的多样性，因为更多的公式被给予了进化的机会，而且群体可能会以花费更长时间为代价找到更好的解决方案。这被称为选择压力，选择可能受计算时间的制约。

交叉（Crossover）

优胜者内随机选择一个子树，替换为另一棵公式树的随机子树。此处的另一棵公式树通常是剩余公式树中适应度最高的。

变异

子树变异（Subtree Mutation）

由 p_subtree_mutation 参数控制。这是一种更激进的变异策略：优胜者的一棵子树将被另一棵完全随机的全新子树代替。

hoist 变异（Hoist Mutation）

由 p_hoist_mutation 参数控制。hoist 变异是一种对抗公式树膨胀（bloating，即过于复杂）的方法：从优胜者公式树内随机选择一个子树 A ，再从 A 里随机选择一个子树 B，然后把 B 提升到 A 原来的位置，用 B 替代 A。hoist 的含义即「升高、提起」。

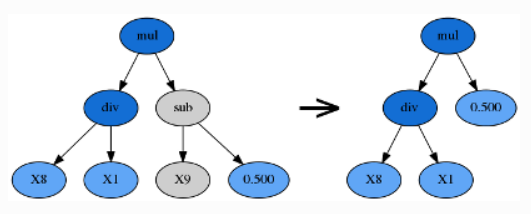
点变异（Point Mutation）

由 p_point_replace 参数控制。一个随机的节点将会被改变，比如加法可以被替换成除法，变量 X0 可以被替换成常数 -2.5。点变异可以重新加入一些先前被淘汰的函数和变量，从而促进公式的多样性。

由于进化过程的黑箱属性，调参很大程度上依赖于用户的直觉和经验。对于实际问题本身的理解也必不可少，如：最终的公式可能有多复杂？

在使用 SymbolicRegressor 时，对目标变量进行标准化（standardization）和区间缩放（min-max-scaling）可以有效避免常数值区间不符的问题。（假如目标变量的区间是 [-1000, 4000]，那么区间为 [-1, 1] 的常数恐怕不会有多大帮助，最终得出的公式只会是一串几乎毫无意义的加法和乘法。）

迭代终止（Termination）

有两种方式可以使进化过程停止。第一种是达到由参数 generation 控制的最大迭代数。第二种方式是，种群中至少有一个公式的适应度超过了某个阈值。如果在处理现实生活中的数据，可能需要做一些测试运行来确定阈值的选择。

膨胀现象（Bloat）

一棵公式树的复杂度有两个方面：深度（树的深度）和长度（节点的总数量）。当公式变得越来越复杂，计算速度也越发缓慢，但它的适应度却毫无提升时，我们称这种现象为膨胀（bloating）。

对抗膨胀的方法如下：

在适应度函数中加入节俭系数（parsimony coefficient），由参数 parsimony_coefficient 控制，惩罚过于复杂的公式。节俭系数往往由实践验证决定。如果过于吝啬（节俭系数太大），那么所有的公式树都会缩小到只剩一个变量或常数；如果过于慷慨（节俭系数太小），公式树将严重膨胀。不过，gplearn 已经提供了 ‘auto’ 的选项，能自动控制节俭项的大小。
使用 hoist 变异，削减过大的公式树。
每一代的进化中，只有一部分样本会被随机选取，用于衡量公式的适应度。此处样本的数量由参数 max_samples 控制。这种做法不仅提升了运算速度、保证了公式的多样性，还允许用户查看每一个公式的 out-of-bag fitness，更为客观。

tips：

1. 遗传编程和遗传规划或遗传程序设计是指代同一类（Genetic Programming，GP）
2. 基因表达式编程（Gene Expression Programming, GEP， 2001 年 F. Candida 提出）

Reference

[1] gplearn 官方文档： https://gplearn.readthedocs.io/en/stable/intro.html#closure

https://blog.csdn.net/weixin_45526117/article/details/129884549