一、树的概念与性质
(一)、树的概念与应用
1、树的概念
定义1 不含圈的图称为无圈图,树是连通的无圈图。( T 3 T_3 T3 是平凡图,即度为 0)

定义2 称无圈图 G G G为森林。
注:
(1) 树与森林都是单图; (单图即简单图,无重边无环的图)
(2) 树与森林都是偶图。

2、树的应用
树是图论中应用最为广泛的一类图。在理论上,由于树的简单结构,常常是图论理论研究的“试验田”。在实际问题中,许多实际问题的图论模型就是树。




(二)、树的性质
定理1 每棵非平凡树至少有两片树叶。
证明 设 P = v 1 v 2 … v k P=v_1v_2…v_k P=v1v2…vk是非平凡树 T T T中一条最长路,则 v 1 v_1 v1与 v k v_k vk在 T T T中的邻接点只能有一个,否则,要么推出 P P P不是最长路,要么推出 T T T中存在圈,这都是矛盾!即说明 v 1 v_1 v1与 v k v_k vk是树叶。(树中最长路的两个端点,所以一定至少两片叶子)
定理 2 图 G G G是树当且仅当 G G G中任意两点都被唯一的路连接。
证明:
“必要性”(图 G G G是树 一定有 G G G中任意两点都被唯一的路连接)
(反证法)若不然,设 P 1 P_1 P1与 P 2 P_2 P2是连接 u u u与 v v v的两条不同的路。则由这两条路的全部或部分将构成一个圈,这与G是树相矛盾。
“充分性”(已知 G G G中任意两点都被唯一的路连接,则图 G G G是树)
首先,因 G G G的任意两点均由唯一路相连,所以 G G G是连通的。
其次,若 G G G中存在圈,则在圈中任取点 u u u与 v v v,可得到连接 u u u与 v v v的两条不同的路,与条件矛盾。
定理 3 设 T T T是 ( n , m ) (n, m) (n,m)树,则: m = n − 1 m = n - 1 m=n−1
证明: “必要性” ( T T T是 ( n , m ) (n, m) (n,m)树 一定有 m = n − 1 m = n - 1 m=n−1)
对 G G G 的顶点作数学归纳,当 n = 1 n=1 n=1 时 m = 0 m=0 m=0 ,等式显然成立;
设 n = k n=k n=k时等式成立。考虑 n = k + 1 n=k+1 n=k+1的树 T T T。 由定理 1 T T T 中至少有两片树叶,设 u u u是 T T T中树叶,考虑 T 1 = T − u T_1=T-u T1=T−u(即去掉一个树叶,顶点变为了 n = k n=k n=k), 则 T 1 T_1 T1为 k k k阶树,于是 m ( T 1 ) = k − 1 m(T_1)=k-1 m(T1)=k−1, 得 m ( T ) = k m(T)=k m(T)=k( 在 T 1 T_1 T1 的基础上加上了 u u u 叶节点对应的边)。这就证明了定理 3。


推论 1 具有 k k k个分支的森林有 n − k n-k n−k条边。
每个分支都满足定理 3: m = n − 1 m = n - 1 m=n−1

定理 4 每个 n n n 阶连通图的边数至少为 n − 1 n-1 n−1. ( m = n − 1 m = n - 1 m=n−1 是说的树的性质,从而树是最小连通图)
握手定理,度之和是边的两倍,如果存在一度顶点,比如树为 m = n − 1 m = n - 1 m=n−1, m ( G ) = 1 2 ∑ v ∈ V ( G ) d ( v ) = n − 1 < n m(G)=\frac12\sum_{v \in V(G)}d(v) = n - 1 < n m(G)=21∑v∈V(G)d(v)=n−1<n ; 又比如两个顶点之间连接了两条边,此时 m ( G ) = 1 2 ∑ v ∈ V ( G ) d ( v ) = n m(G)=\frac12\sum_{v \in V(G)}d(v) = n m(G)=21∑v∈V(G)d(v)=n;所以如果没有一度顶点,则 m ( G ) = 1 2 ∑ v ∈ V ( G ) d ( v ) ≥ n m(G)=\frac12\sum_{v \in V(G)}d(v)\geq n m(G)=21∑v∈V(G)d(v)≥n

定理5 任意树 T T T的两个不邻接顶点之间添加一条边后,可以得到唯一圈。



其中的 2 m ( G ) = ∑ v ∈ V ( G ) d ( v ) ≥ k − 1 + k + 2 ( n − k ) = 2 n − 1 > 2 n − 2 2m(G)=\sum_{v \in V(G)}d(v)\geq k-1+k+2(n-k)=2n-1>2n-2 2m(G)=∑v∈V(G)d(v)≥k−1+k+2(n−k)=2n−1>2n−2 其中的 k − 1 + k + 2 ( n − k ) k-1+k+2(n-k) k−1+k+2(n−k) 的由来如下:
- 至多 k − 1 k - 1 k−1 个一度顶点,则取 k − 1 k - 1 k−1 个一度顶点
- Δ ≥ k \Delta ≥ k Δ≥k 则取一个度为 k 的顶点。
- 剩下全部认为是度为 2 2 2 的顶点, 2 ( n − k ) 2(n - k) 2(n−k)
- 因此三项相加组成了最小的度 k − 1 + k + 2 ( n − k ) k-1+k+2(n-k) k−1+k+2(n−k)

树的度序列问题:
在第一章中,介绍了判定一个非增非负序列是否为简单图的度序列定理。下面介绍一个判定非增非负序列是否为树的度序列的简单方法。
定理 6 设 S = { d 1 , d 2 , … , d n } S=\{d_1,d_2,…,d_n\} S={d1,d2,…,dn} 是 n n n 个正整数序列,它们满足: d 1 ≧ d 2 ≧ … ≧ d n d_1≧ d_2 ≧ … ≧ d_n d1≧d2≧…≧dn , ∑ d i = 2 ( n − 1 ) ∑d_i=2(n-1) ∑di=2(n−1). 则存在一颗树 T T T,其度序列为 S S S。(树 T T T 满足 m = n − 1 m = n - 1 m=n−1, ∑ d i = 2 m = 2 ( n − 1 ) ∑d_i = 2m = 2(n - 1) ∑di=2m=2(n−1) )
证明: 对 n n n作数学归纳。
当 n = 1 n=1 n=1和2时,结论显然。
假设对 n = k n=k n=k时结论成立。设 n = k + 1 n=k+1 n=k+1
首先, 序列中至少一个数为 1,否则,序列和大于 2k,与条件相矛盾!
所以, d k + 1 = 1 d_{k+1}=1 dk+1=1. 我们从序列中删掉 d 1 d_1 d1 和 d k + 1 d_{k+1} dk+1, 增加数 d ∗ = d 1 − 1 d^* =d_1-1 d∗=d1−1 放在它应该在的位置。得到序列 S 1 S_1 S1 . 该序列含 k k k个数,序列和为 2 ( k − 1 ) 2(k-1) 2(k−1), 由归纳假设,存在树 T 1 T_1 T1,它的度序列为 S 1 S_1 S1.
现在,增加结点 v v v,把它和 T 1 T_1 T1中点 d ∗ d^* d∗相连得到树 T T T。树 T T T为所求。
(三)、树的中心与形心(形心自行了解,不做要求)
1、树的中心概念与性质
(1) 图的顶点的离心率
e
(
v
)
=
max
{
d
(
μ
,
v
)
∣
u
∈
V
(
G
)
}
e(v)=\max\left\{d(\mu, v)\big|u\in V(G)\right\}
e(v)=max{d(μ,v)
u∈V(G)}
(2) 图的半径(最小离心率)
r
(
G
)
=
min
{
e
(
v
)
∣
v
∈
V
(
G
)
}
r(G)=\min\left\{e(v)|v \in V(G)\right\}
r(G)=min{e(v)∣v∈V(G)}
(3) 图的直径:最大离心率。
(4) 图的中心点:离心率等于半径的点。
(5) 图的中心:中心点的集合。
定理7 每棵树的中心由一个点或两个相邻点组成。

2、树的形心概念与性质
设 u u u是树 T T T的任意一个顶点,树 T T T在顶点 u u u的分支是指包含 u u u作为一个叶点的极大子树,其分支数为顶点 u u u的度数;树 T T T在 u u u点的分支中边的最大数目称为点 u u u的权;树 T T T中权值最小的点称为它的一个形心点。全体形心点的集合称为树 T T T的形心。

定理 8 每一棵树有一个由一个点或两个邻接的点组成的形心。
P43 习题2 : 1,2,3,4,5,6
二、生成树
(一)、生成树的概念与性质
1、生成树的概念
定义 1 图 G G G的一个生成子图 T T T如果是树,称它为 G G G的一棵生成树;若 T T T为森林,称它为 G G G的一个生成森林。
生成树的边称为树枝, G G G中非生成树的边称为弦。

2、生成树的性质
定理 1 每个连通图至少包含一棵生成树。
证明: 如果连通图 G G G是树,则其本身是一棵生成树;
若连通图 G G G中有圈 C C C,则去掉 C C C中一条边后得到的图仍然是连通的,这样不断去掉 G G G中圈,最后得到一个 G G G的无圈连通子图 T T T,它为 G G G的一棵生成树。
定理1 的证明实际上给出了连通图 G G G的生成树的求法,该方法称为破圈法。
利用破圈法,显然也可以求出任意图的一个生成森林。
推论 若 G G G是 ( n , m ) (n, m) (n,m)连通图,则 m ≥ n − 1 m ≥ n-1 m≥n−1
证明: G G G 包含一颗生成树 T T T,因此
连通图 G G G的生成树一般不唯一!
(二)、生成树的计数
1、凯莱递推计数法
定义2 图 G G G的边 e e e称为被收缩,是指删掉 e e e后,把 e e e的两个端点重合,如此得到的图记为 G . e G.e G.e

用 τ ( G ) τ(G) τ(G) 表示 G G G 的生成树棵数。
定理 2 (Cayley) 设
e
e
e是
G
G
G的一条边,则有:
τ
(
G
)
=
τ
(
G
−
e
)
+
τ
(
G
∙
e
)
\tau\left(G\right)=\tau\left(G-e\right)+\tau\left(G\bullet e\right)
τ(G)=τ(G−e)+τ(G∙e)
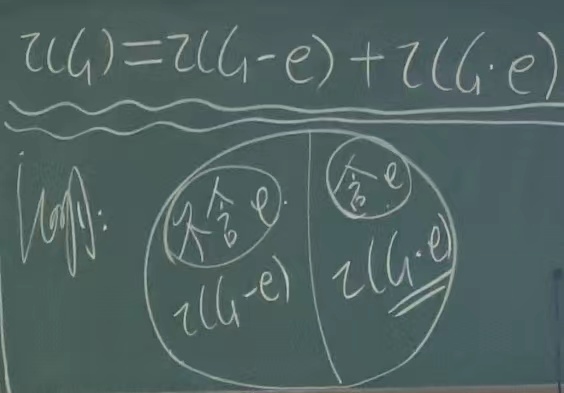
实际上公式中的两个加和表示:所有生成树中,含有 e e e 这条边,与不含这条边的所有和
证明: 对于 G G G的一条边 e e e来说, G G G的生成树中包含边 e e e的棵数为 τ ( G . e ) τ(G.e ) τ(G.e),而不包含 e e e的棵数为 τ ( G − e ) τ (G-e) τ(G−e).
注意:在画图过程中,什么时候停止:(1)如果继续划分 G − e G-e G−e导致不连通。(2)环无法再继续 G ⋅ e G·e G⋅e

定理: τ ( K n ) = n n − 2 τ(K_n) = n^{n - 2} τ(Kn)=nn−2
凯莱公式的缺点之一是计算量很大,其次是不能具体指出每棵生成树。
2、关联矩阵计数法
定义3 : n × m n×m n×m 矩阵的一个阶数为 m i n { n , m } min\{n, m\} min{n,m}的子方阵,称为它的一个主子阵;主子阵的行列式称为主子行列式。
显然,当 n < m n<m n<m时, n × m n×m n×m矩阵 C m n C_m^n Cmn个主子阵。(主子阵即方阵)
非奇异表示行列式不能等于0,于是将所有主子阵中行列式等于 0 的去掉,剩下的主子阵的个数即为生成树个数。
定理 3 设 A m A_m Am 是连通图 G G G 的基本关联矩阵的主子阵,则 A m A_m Am 非奇异的充分必要条件是相应于 A m A_m Am 的列的那些边构成 G G G 的一棵生成树。
该定理给出了求连通图G的所有生成树的方法:
(1) 写出G的关联矩阵,进一步写出基本关联矩阵,记住参考点;
(2) 找出基本关联矩阵的非奇异主子阵,对每个这样的主子阵,画出相应的生成树。





3、矩阵树定理
定理4 (矩阵树定理) 设 G G G 是顶点集合为 V ( G ) = { v 1 , v 2 , … , v n } V(G)=\{v_1, v_2,…, v_n\} V(G)={v1,v2,…,vn},的图,设 A = ( a i j ) A=(a_{ij}) A=(aij)是 G G G的邻接矩阵, C = ( c i j ) C=(c_{ij}) C=(cij)是 n n n阶方阵,其中:
c i j = { d ( v i ) , i = j − a i j , i ≠ j c_{ij}=\begin{cases}d(v_i),i=j\\-a_{ij},i\neq j\end{cases} cij={d(vi),i=j−aij,i=j
则 G G G的生成树棵数为 C C C的任意一个余子式的值。
矩阵树定理的证明很复杂,在此略去证明;
定理中的矩阵
C
C
C又称为图的拉普拉斯矩阵,又可定义为:
C
=
D
(
G
)
−
A
(
G
)
\begin{aligned}C&=D\left(G\right)-A\left(G\right)\end{aligned}
C=D(G)−A(G)
其中, D ( G ) D(G) D(G)是图的度对角矩阵,即主对角元为对应顶点度数,其余元素为0。 A ( G ) A(G) A(G)是图的邻接矩阵。
余子式: 设 ∣ A ∣ |A| ∣A∣是一个 n n n 阶行列式,划去的第 i i i行及第 j j j列,剩下的 ( n − 1 ) 2 (n-1)^2 (n−1)2个元素按照原来的顺序组成了一个 n − 1 n-1 n−1行列式,这个行列式称为 ∣ A ∣ |A| ∣A∣的第 ( i , j ) (i,j) (i,j)元素的余子式,记为 M i j M_{ij} Mij .
代数余子式: 设 ∣ A ∣ |A| ∣A∣是一个 n n n 阶行列式, M i j M_{ij} Mij是 ∣ A ∣ |A| ∣A∣的第 ( i , j ) (i,j) (i,j)元素的余子式,定义 ∣ A ∣ |A| ∣A∣的第 ( i , j ) (i,j) (i,j)元素的代数余子式为: A y = ( − 1 ) i + j M i j A_y=(-1)^{i+j}M_{ij} Ay=(−1)i+jMij
三阶行列式
D
3
=
∣
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
∣
\mathrm{D}_3=\begin{vmatrix}\mathrm{a}_{11}&\mathrm{a}_{12}&\mathrm{a}_{13}\\\mathrm{a}_{21}&\mathrm{a}_{22}&\mathrm{a}_{23}\\\mathrm{a}_{31}&\mathrm{a}_{32}&\mathrm{a}_{33}\end{vmatrix}
D3=
a11a21a31a12a22a32a13a23a33
①将第一、二列平移到行列式右侧
②如图做出六条斜对角线
③对角线上的元素相乘,红色相加的和 减去 蓝色相加的和
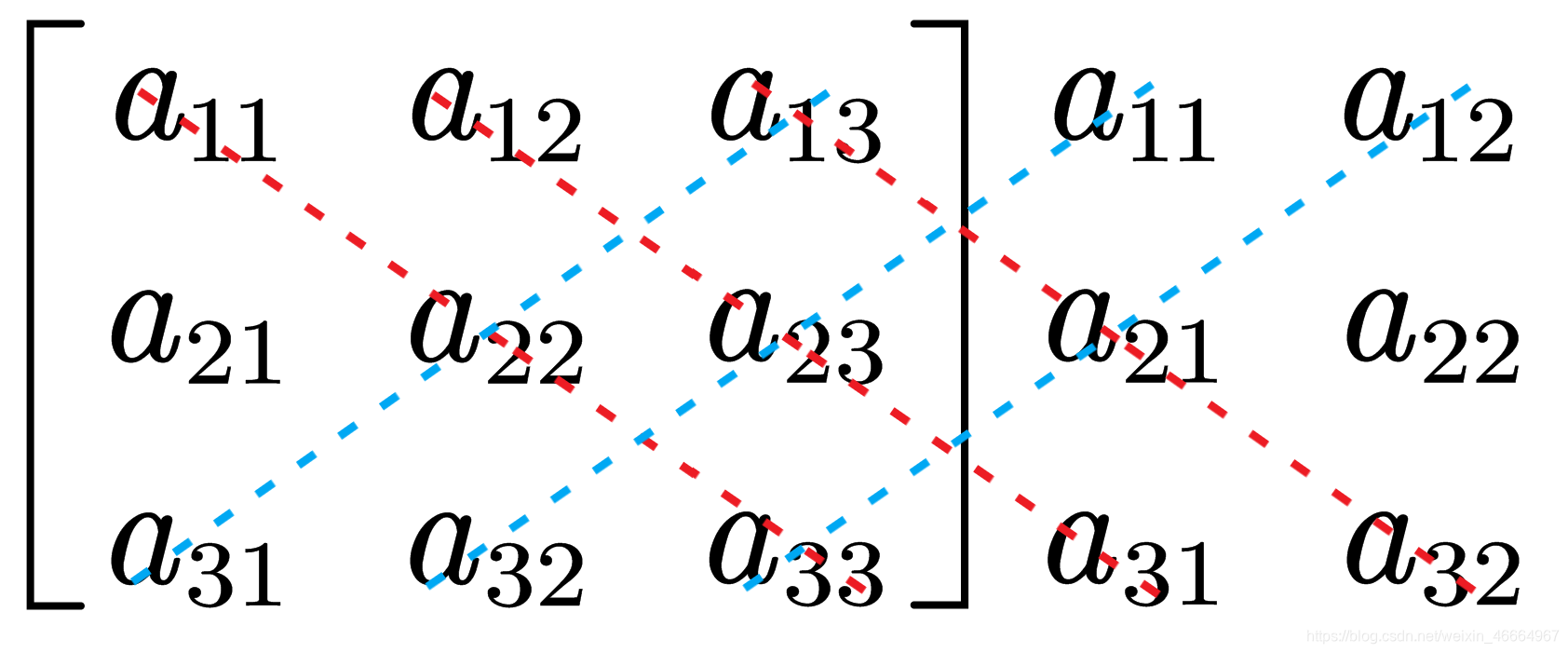
D 3 = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 − a 11 a 23 a 32 − a 12 a 21 a 33 \mathrm{D}_3=\mathrm{a}_{11}\mathrm{~a}_{22}\mathrm{~a}_{33}+\mathrm{~a}_{12}\mathrm{~a}_{23}\mathrm{~a}_{31}+\mathrm{~a}_{13}\mathrm{~a}_{21}\mathrm{~a}_{32}-\mathrm{a}_{13}\mathrm{a}_{22}\mathrm{a}_{31}-\mathrm{a}_{11}\mathrm{a}_{23}\mathrm{a}_{32}-\mathrm{a}_{12}\mathrm{a}_{21}\mathrm{a}_{33} D3=a11 a22 a33+ a12 a23 a31+ a13 a21 a32−a13a22a31−a11a23a32−a12a21a33
代数余子式法
例: D
3
=
∣
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
∣
以第一行展开
,
得
D
3
=
=
(
−
1
)
1
+
1
a
11
M
11
+
(
−
1
)
1
+
2
a
12
M
12
+
(
−
1
)
1
+
3
a
13
M
13
=
a
11
∣
a
22
a
23
a
32
a
33
∣
−
a
12
∣
a
21
a
23
a
31
a
33
∣
+
a
13
∣
a
21
a
22
a
31
a
32
∣
\begin{gathered} \text{例: D}_3=\begin{vmatrix}\mathrm{a}_{11}&&\mathrm{a}_{12}&&\mathrm{a}_{13}\\\mathrm{a}_{21}&&\mathrm{a}_{22}&&\mathrm{a}_{23}\\\mathrm{a}_{31}&&\mathrm{a}_{32}&&\mathrm{a}_{33}\end{vmatrix} \\\\ 以第一行展开,得D_3= \\\\ =\left(-1\right)^{1+1}\mathrm{a}_{11}\mathrm{M}_{11}+\left(-1\right)^{1+2}\mathrm{a}_{12}\mathrm{M}_{12}+\left(-1\right)^{1+3}\mathrm{a}_{13}\mathrm{M}_{13} \\\\ =\mathrm{a}_{11}\left.\begin{vmatrix}\mathrm{a}_{22}&\mathrm{a}_{23}\\\mathrm{a}_{32}&\mathrm{a}_{33}\end{vmatrix}\right.-\mathrm{a}_{12}\left.\begin{vmatrix}\mathrm{a}_{21}&\mathrm{a}_{23}\\\mathrm{a}_{31}&\mathrm{a}_{33}\end{vmatrix}\right.+\mathrm{a}_{13}\left.\begin{vmatrix}\mathrm{a}_{21}&\mathrm{a}_{22}\\\mathrm{a}_{31}&\mathrm{a}_{32}\end{vmatrix}\right. \end{gathered}
例: D3=
a11a21a31a12a22a32a13a23a33
以第一行展开,得D3==(−1)1+1a11M11+(−1)1+2a12M12+(−1)1+3a13M13=a11
a22a32a23a33
−a12
a21a31a23a33
+a13
a21a31a22a32
对于任一行(列)都可进行展开

上图的拉式矩阵如下可得:

对于下面余子式的求解:首先将第二列到最后一列加到第一列,从而,第 1 列元素变为全为 1,然后将第 1 列依次加到后面每列,使得除了第一行第一列的剩下矩阵只有对角线上有元素 n,然后进一步对第一行使用代数余子式法求行列式。

(三)、回路系统简介
定义 4 设 T T T是连通图 G G G的一棵生成树,把属于 G G G但不属于 T T T的边称为 G G G关于 T T T的连枝, T T T中的边称为 G G G关于 T T T的树枝。
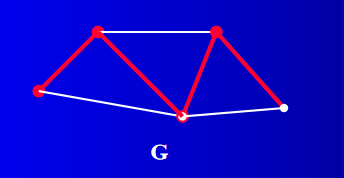
在上图中,红色边导出图的一棵生成树。则红色边为 G G G对应于该生成树的树枝,白色边为 G G G对应于该生成树的连枝。
定义5 设 T T T是连通图 G G G的一棵生成树,由 G G G的对应于 T T T一条连枝与 T T T中树枝构成的唯一圈 C C C,称为 G G G关于 T T T的一个基本圈或基本回路。若 G G G是 ( n , m ) (n, m) (n,m)连通图,把 G G G对应于 T T T的 m − n + 1 m-n+1 m−n+1个基本回路称为 G G G对应于 T T T的基本回路组。记为 C f C_f Cf .

基本回路的性质:
定理4 设 T T T是连通图 G = ( n , m ) G=(n, m) G=(n,m) 的一棵生成树, C 1 , C 2 , … , C m − n + 1 C_1, C_2,…,C_{m-n+1} C1,C2,…,Cm−n+1 是 G G G对应于 T T T的基本回路组。定义: 1. G i = G i , 0. G i = Φ , G i 1.G_i=G_i , 0.G_i=Φ,G_i 1.Gi=Gi,0.Gi=Φ,Gi是 G G G的回路。则 G G G的回路组作成的集合对于该乘法和图的对称差运算来说作成数域 F = { 0 , 1 } F=\{0,1\} F={0,1} 上的 m − n + 1 m-n+1 m−n+1 维向量空间。
说明: 连通图 G G G的所有回路作成子图空间的一个子空间,该空间称为回路空间或回路系统。

P43 习题2 : 12, 14, 15
三、最小生成树


(一)、克鲁斯克尔算法
1、算法思想
从 G G G中的最小边开始,进行避圈式扩张。
2、算法


定理1 由克鲁斯克尔算法得到的任何生成树一定是最小生成树。(证明略)

(二)、管梅谷的破圈法
破圈法求最小生成树的求解过程是:从赋权图G的任意圈开始,去掉该圈中权值最大的一条边,称为破圈。不断破圈,直到G中没有圈为止,最后剩下的G的子图为G的最小生成树。

(三)、Prim算法
对于连通赋权图 G G G的任意一个顶点 u u u,选择与点 u u u关联的且权值最小的边作为最小生成树的第一条边 e 1 e_1 e1;
在接下来的边 e 2 , e 3 , … , e n − 1 e_2, e_3 ,…, e_{n-1} e2,e3,…,en−1 , 在与一条已经选取的边只有一个公共端点的的所有边中,选取权值最小的边。
用反证法可以证明该算法。即证明:由Prim算法得到的生成树是最小生成树。(证明略)

(四)、根树简介
定义2: 一棵树 T T T,如果每条边都有一个方向,称这种树为有向树。对于 T T T的顶点 v v v来说,以点 v v v为终点的边数称为点 v v v的入度,以点 v v v为起点的边数称为点 v v v的出度。入度与出度之和称为点 v v v的度。
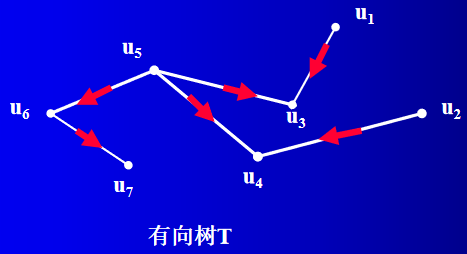
注: 指出上图中顶点的入度、出度和度。
定义3: 一棵非平凡的有向树 T T T,如果恰有一个顶点的入度为 0,而其余所有顶点的入度为1,这样的的有向树称为根树。其中入度为0的点称为树根,出度为0的点称为树叶,入度为1,出度大于1的点称为内点。又将内点和树根统称为分支点。
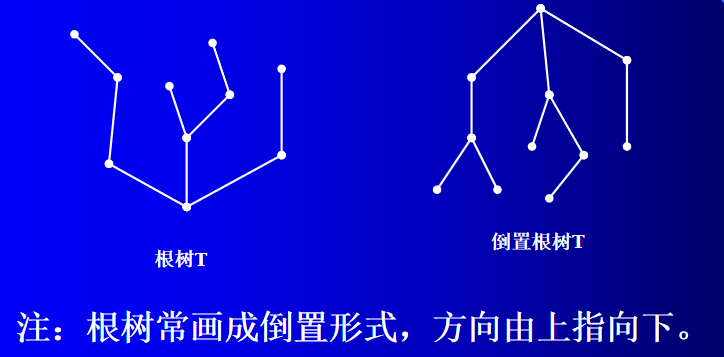
定义4: 对于根树 T T T,顶点 v v v到树根的距离称为点 v v v的层数;所有顶点中的层数的最大者称为根树 T T T的树高。
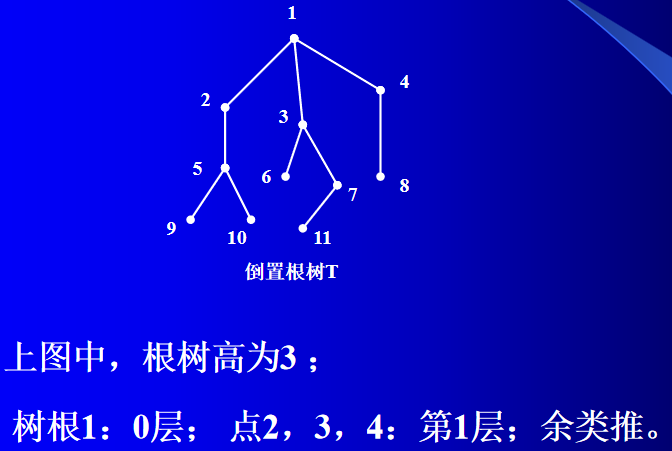
计算机中数据结构常采用根树结构。族谱图是根树。
定义5: 对于根树 T T T,若规定了每层顶点的访问次序,这样的根树称为有序树。
注: 一般次序为从左至右。有时也用边的次序代替顶点次序。
定义6: 对于根树 T T T,由点 v v v及其 v v v的后代导出的子图,称为根树的子根树。
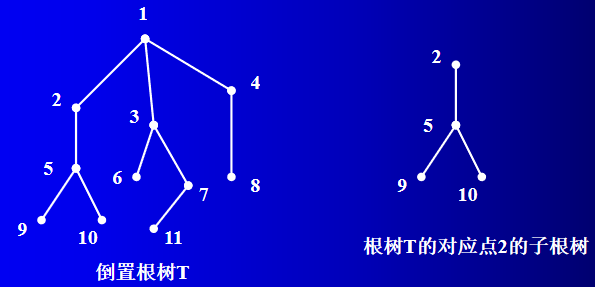
定义7: 对于根树 T T T,若每个分支点至多 m m m个儿子,称该根树为 m m m元树;若每个分支点恰有 m m m个儿子,称它为完全 m m m元树。

对于完全 m m m元树 T T T,有如下性质:
定理2 在完全 m m m 元树 T T T 中,若树叶数为 t t t , 分支点数为 i i i , 则:
( m − 1 ) i = t − 1 (m - 1) i = t - 1 (m−1)i=t−1
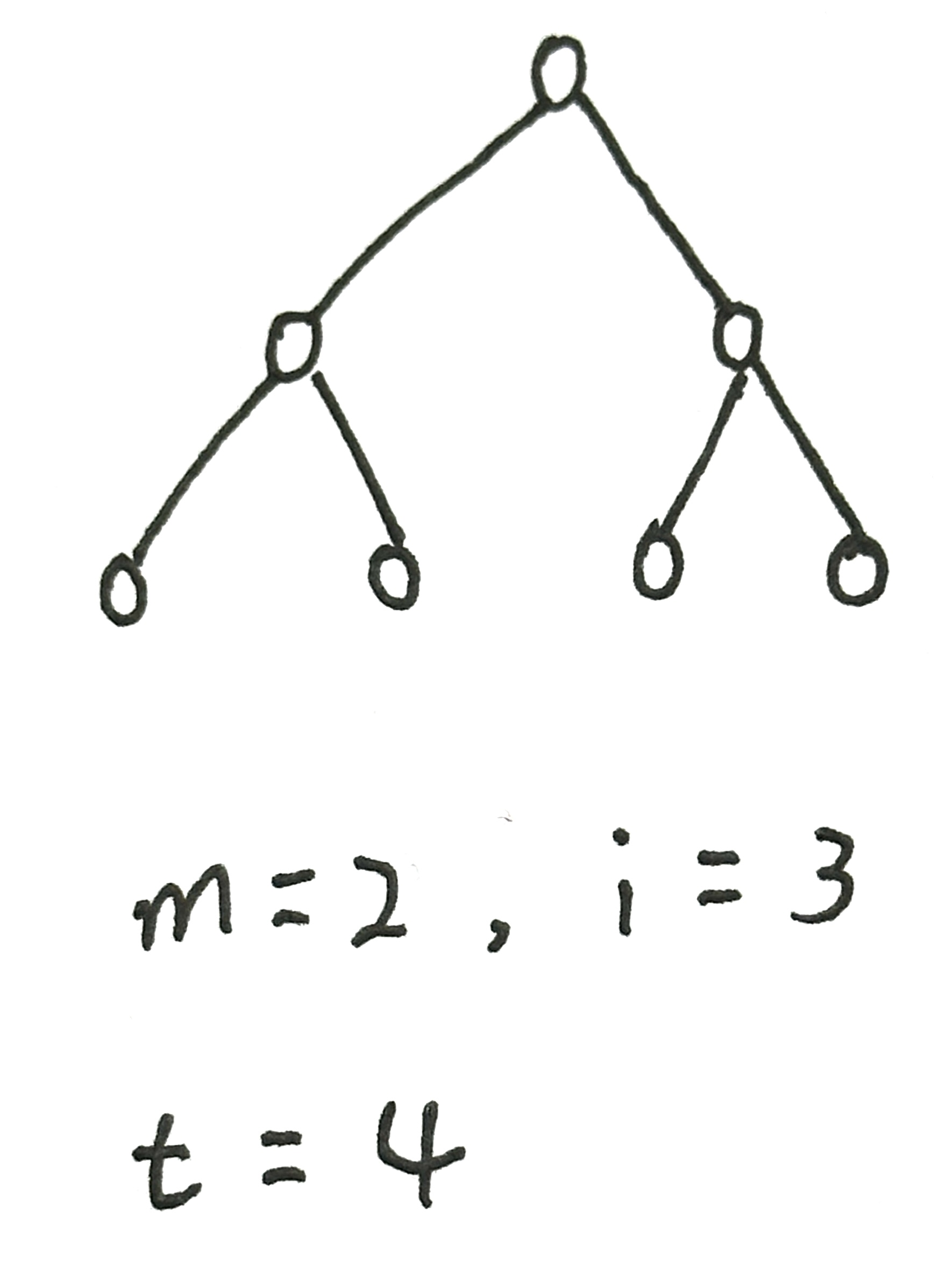
证明: 一方面,由树的性质得:(注意:下述的 m ( T ) m(T) m(T) 表示树 T T T 的边数, m m m 表示 m m m 元)
m ( T ) = ( i + t ) − 1 ( 1 ) 树的性质, m ( T ) = n − 1 \begin{aligned}m(T)=(i+t)-1 &&&&&&&&(1)\end{aligned} \text{ 树的性质, $m(T) = n - 1$} m(T)=(i+t)−1(1) 树的性质, m(T)=n−1
另一方面,由握手定理得:
2 m ( T ) = t + m + ( i − 1 ) ( m + 1 ) ( 2 ) 2m(T) = t + m + (i-1)(m+1) ~~~~~~~~~~~ (2) 2m(T)=t+m+(i−1)(m+1) (2)
- t t t 表示 t t t 个叶子
- m m m 表示树根, m m m 元所以树根度为 m m m
- 剩下的内点 i − 1 i - 1 i−1 个,每个内点的入度为 1 1 1,出度为 m m m,因此度为 m + 1 m + 1 m+1,总度数为 ( i − 1 ) ( m + 1 ) (i-1)(m+1) (i−1)(m+1)
由(1)与(2)消去m (T)得:
( m − 1 ) i = t − 1 \left.\left(\begin{array}{cc}m-1\end{array}\right.\right)i=\begin{array}{cc}t-1\end{array} (m−1)i=t−1
例 5 一台计算机,它有一条加法指令,可以计算3个数的和。如果要求9个数的和,问至少执行多少次加法指令?(求内点 i i i 的数量,即为执行次数)

在 m m m元树中,应用最广泛的是二元树,原因是它在计算机中容易处理。
1、有序树转换为二元树
对于一棵有序树,常要转化为二元树。方法是: (左子有兄弟的方式构建二元树)
- (1) 从根开始,保留每个父亲同其最左边儿子的连线,撤销与别的儿子的连线;
- (2) 兄弟间用从左至右的有向边连接;
- (3) 按如下方法确定二元树中结点的左右儿子:直接位于给定结点下面的儿子,作为左儿子,对于同一水平线上与给定结点右邻的结点,作为右儿子,依此类推。

2、二元树的遍历问题
找到一种方法,能系统访问根结点,使得每个结点恰好访问一次。有三种常用方法:
(1) 先根次序遍历:
- 1) 访问根;
- 2)按先根次序遍历根的左子树;
- 3)按先根次序遍历根的右子树;

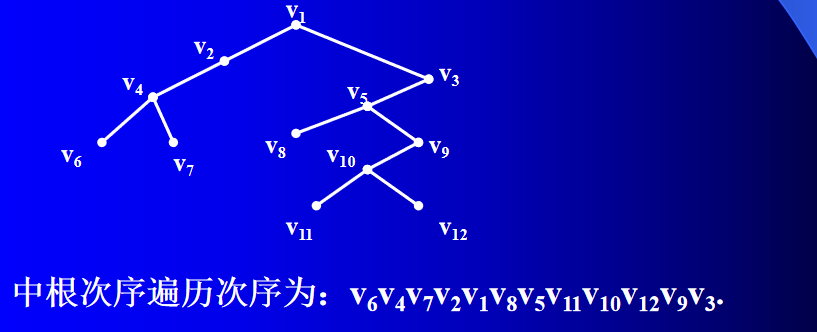
(2) 中根次序遍历:
- 1)按中根次序遍历根的左子树;
- 2) 访问根;
- 3)按中根次序遍历根的右子树;
(3)后根次序遍历:
- 1)按后根次序遍历根的左子树;
- 2)按后根次序遍历根的右子树;
- 3) 访问根;

3、最优二元树
定义8 设 T T T是一棵二元树,若对所有 t t t片树叶赋权值 w i ( 1 ≦ i ≦ t ) w_i(1≦i≦t) wi(1≦i≦t), 且权值为 w i w_i wi 的树叶层数为 L ( w i ) L(w_i) L(wi), 称:
W ( T ) = ∑ i = 1 t w i L ( w i ) \begin{aligned}W\left(T\right)&=\sum_{i=1}^{t}w_{i}L\left(w_{i}\right)\end{aligned} W(T)=i=1∑twiL(wi)
为该赋权二元树的权。而在所有赋权为 w i w_i wi的二元树中 W ( T ) W(T) W(T)最小的二元树称为最优二元树。
4、哈夫曼算法


为什么要依次选择最小的???
因为最优二元树满足 W ( T ) = ∑ i = 1 t w i L ( w i ) \begin{aligned}W\left(T\right)&=\sum_{i=1}^{t}w_{i}L\left(w_{i}\right)\end{aligned} W(T)=i=1∑twiL(wi),其中 W ( T ) W(T) W(T) 最小, L ( w i ) L(w_i) L(wi) 为树叶层数,因此让层数大的权重尽可能小,所以依次选择更小的从底层逐步构建。
作业
P43 习题2 : 16, 17, 18
























 291
291

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








