本文详细介绍了数据流分析的基础，包括迭代算法的视角、偏序集的概念、上界与下界、格的类型以及全格。通过格理论，阐述了不动点定理在数据流分析中的应用，特别是如何关联迭代算法与不动点定理，确保算法能到达不动点。此外，文章还探讨了May和Must分析的差异，以及常量传播和工作列表算法的优化。
🔗 课程链接：李樾老师和谭天老师的：
南京大学《软件分析》课程05（Data Flow Analysis - Foundations I）_哔哩哔哩_bilibili
目录
4.1 从另一个视角看迭代算法（Iterative Algorithm）
4.1.1 回顾 May&Forward Analysis 的迭代算法
4.3 上界和下界（Upper and Lower Bounds）
4.4.3 全格（Complete Lattice）⭐==》 top and bottom
4.6.2 不动点定理 Fixed-Point Theorem
4.8 从Lattice的视角看 May/ Must 分析⭐⭐
4.9 Distributivity(分配性) and MOP
4.10 Constant Propagation 常量传播
4.11 Worklist 算法，一种迭代算法的优化（更常用）
第四章 数据流分析——基础
4.1 从另一个视角看迭代算法（Iterative Algorithm）
4.1.1 回顾 May&Forward Analysis 的迭代算法
首先来回顾一下上一章节里介绍的Reaching Definitions的算法，是may analysis，正向传播，如下图所示：
4.1.2 从另一视角看迭代算法
1. 接下来，我们从数学的视角来看迭代算法，文字定义如下：
- 给定一个具有k个节点的CFG，迭代算法对每次迭代中的每个节点n更新OUT[n]；
- 假设数据流分析中的值域(domain)为V，那么我们可以定义一个k元组(k-tuple)以保存每次迭代后的分析值。
- 这个k元组 内容为
表示为
， 记作
- 例如说Reaching definitions分析中，值域V就是所有程序中的definitions，有了这个值域，我们就可以定义k元组：k对应k个节点，然后k元组的值域就是每个节点的OUT值，每个OUT值对应的就是1个V，所以k元组对应的值域就是V的product，也就是(V1 × V2 ... × Vk)，记为V的k次方。
- 这个k元组 内容为
- 每一次迭代都可以看作是一个动作：通过应用传递函数和控制流处理，将
的元素映射为
。
- 然后，该算法以迭代的方式输出一系列k元组，直到k元组与最后一个连续迭代的k元组相同。
2. 下一步，我们用具体的例子和符号来进一步理解上边的文字，：
如下图所示的分析流程的代码
我们用符号来表示每一次迭代如下图所示：
将其做了批注如下图所示：
所以根据这个例子来看，可以很直观地看出，最后达到了不动点(fixed point)，理解了这个过程，会对我们后续理解不动点定理，非常有帮助。
3. 关于这个不动点，这个X = F(X) 数学表达形式，提出三个问题：
- 算法是否一定会终止或到达不动点，或者说一定会给数据流分析一个解决方案？
- 如果可以，那么是否只有一个解决方案或不动点？如果不止一个，我们的方案是否是最好最精确的？
- 算法何时到达不动点，或者说我们何时得到解决方案？
为了回答这三个问题，我们需要先学习一些数学知识：
4.2 偏序（Partial Order）
从这节开始，是很多离散数学方面的知识点，如果离散忘掉了或者还不是很懂，一定还是要好好看的，这里的所有数学知识，后续都会用到。
1. 定义
意思就是：我们定义一个偏序集(poset)为一个对(P, ⊑)，其中二元关系符⊑定义了在数据集P上一种偏序关系，并且⊑拥有以下3个性质：
- ∀ x ∈ P, x ⊑ x（自反性，Reflexivity）
- ∀x, y ∈ P, x ⊑ y ∧ y ⊑ x ⟹ x = y （反对称性，Antisymmetry）
- ∀x, y, z ∈ P, x ⊑ y ∧ y ⊑ z ⟹ x ⊑ z（传递性, Transitivity）
如果⊑满足这三个性子，就说明构成一个偏序集。
2. 举个例子
① 整数集上的小于等于关系≤ ，满足这三个性质，所以是偏序关系
② 整数集上的小于关系＜，不满足自反性，所以不是偏序关系
③ 英文字符串中的子串关系，是偏序关系
3. 进一步理解偏序
但是其实如例3中的 pin 和sin ，他们之间就没有这个子串关系，但是这并不妨碍定义的正确。实际上，偏序(partial)为什么不叫全序呢，可以这么理解，对于集合P中的一对集合元素来说，它们也可以是incomparable(不互相比较)的；换句话说，并不是P中的每对元素都必须满足偏序关系。
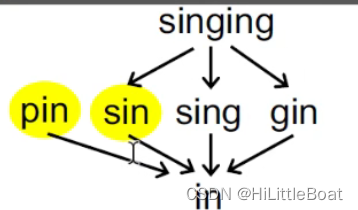
再举个例子：
④ 子集关系⊆ 也是偏序关系
上边这个图要记住，后续会经常拿出来用。在后续的内容离，可以将偏序关系粗略地理解为小于等于关系，这样方便理解，而且基本上不影响证明含义。
4.3 上界和下界（Upper and Lower Bounds）
1. 定义
① 给定偏序集(P, ⊑)及子集S，满足S⊆P，则有
- 若∀x ∈ S, x ⊑ u,那么u ∈ P是子集S的上界 upper bound
- 若∀x ∈ S, l ⊑ x,那么 l ∈ P是子集S的下界 lower bound
如下图所示，灰色区域S即为P的一个子集，其上界和下界分别是{a,b,c} 和 {}
因为上界和下界可以不只是1个，所以有了如下概念：
② 最小上界⊔S(lub / join)和最大下界⊓S(glb / meet)：
- 如果对每一个S的上界，都有⊔S⊑ u，则称其为最小上界（least upper bound, 简称lub or join）记作⊔S
- 如果对每一个S的下界，都有 l ⊑⊓S，则称其为最大下界（greatest lower bound, 简称glb or meet）记作⊓S
如下图所示，最小上界、最大下界
③ 通常来说，如果S仅包含两个元素a, b （S={a, b}），那么：
- ⊔S能被写作 a ⊔ b (a join b)
- ⊓S能被写作 a ⊓ b (a meet b)
2. 性质
- 并不是所有偏序集都有最小上界和最大下界
- 如果有最小上界或者最小下界，则是唯一的
证明：
假设有两个最小上界，根据反对称性，这两个上界是相同的
4.4 格， 半格，全格，乘积格
4.4.1 格（Lattice）⭐
1. 定义
给定一个偏序集(P，⊑ )，对 ∀ a, b∈P，如果a ⊔ b和a ⊓ b都存在，则这个偏序集(P，⊑)称为一个格（Lattice）。
“格” 可能是描述这种上下都有边界的抽象格子
2. 例子：
① 小于等于关系≤ 是“格”吗？—— 是的，因为⊔就是max，⊓就是min，且都存在
② 英文字符串中的子串关系是格吗？——不是。
③ 子集关系，是格吗？—— 是。join 就是∪，meet就是∩
4.4.2 半格（Semilattice）
1. 定义
给定一个偏序集(P，⊑ )，对 ∀ a, b∈P，
- 如果只有 a ⊔ b 存在，则称偏序集为一个join semilattice
- 如果只有 a ⊓ b 存在，则称偏序集为一个meet semilattice
4.4.3 全格（Complete Lattice）⭐==》 top and bottom
1. 定义
给定一个Lattice格 (P，⊑ )，对于P的任意子集S，如果集合S的最小上界⊔S和最大下界⊓S都存在，则(P，⊑)称为一个全格（Complete Lattice）。
格是说任意两个元素之间，而全格是说任意两个子集之间
“全格”可能是在描述一个完整的格，而每个子格，都是一个格。
2. 例子
① 小于等于关系≤ 是全格吗？—— 不是全格，假如说子集S包含所有正整数，它就没有上界（+∞），但是是格，因为任意两个元素，室友上下的。
② 子集关系，是全格吗？——是！
3. 引入两个重要概念：top和bottom ⭐
对每一个全格 (P，⊑ )，都有
- 一个最大(greatest)的元素 ⊤ = ⊔ P， 称为 top
- 一个最小(least) 的元素 ⊥= ⊓ P ，称为 bottom
如下图，还是这个子集的经典例子，top就是{a,b,c}，bottom为{}
4. 性质
任意有穷(finite)的lattice格，都是complete lattice全格
注意：反过来说，全格一定是有穷的吗？
——不一定，比如说，0和1之间，所有的实数的小于等于关系，虽然有边界，但是是无穷的
在数据分析中，基本上用到的都是finite 也是 complete的，即 有穷的全格
4.4.4 乘积格（Product Lattice）
1. 定义
意思就是：给定n个lattice，L1 = (P1, ⊑1), L2 = (P2, ⊑2), …, Ln = (Pn, ⊑n)，如果每个lattice都存在对应的⊔i(最小上界)和⊓i(最大下界)，那么我们得到一个Product Lattice（乘积格） Ln = (P, ⊑)（n是上标，代表n个lattice的乘积 ），可以有如下定义：
- P = P1 × … × Pn （集合域）
- (x1, …, xn) ⊑ (y1, …, yn) ⟺ (x1 ⊑ y1) ∧ … ∧ (xn ⊑ yn) （偏序关系）
- (x1, …, xn) ⊔ (y1, …, yn) = (x1 ⊔1 y1, …, xn ⊔n yn) （最小上界）
- (x1, …, xn) ⊓ (y1, …, yn) = (x1 ⊓1 y1, …, xn ⊓n yn) （最大下界，乘积格任意两个元素的最大下界，就是每个格的两个元素的最大下界）
2. 性质
- 乘积格也是格
- 如果构成L的是一系列complete lattice(全格)的乘积，那么L也是complete lattice。
4.5 基于格的数据流分析框架
有了上述数学的基础，就可以正式进入到数据流分析的理论部分。
1. 数据流分析主要由三个部分组成(D, L, F)
- D: 数据流的方向(direction)：forwards 或 backwards
- L: 包含值域V和一个meet ⊓ 或 join ⊔ 操作符的格(lattice)
- F: 一系列值域V到V的转换函数(transfer funtion)
如下图所示，左边是一个may分析的某一步骤，可以看出分析的过程其实就是右侧的，从bottom 往上走的过程。
所以，数据流分析可以被看做是迭代地在格上使用转换函数和meet/join操作。
2. 再来回顾一下我们之前提出的一些问题：
- 算法一定能停止或者一定可以达到不动点吗？或者说总有一个解吗？
——回忆“OUT never shrinks” ，这与单调性有关
- 如果一定会停下，那会由多个不动点吗？如果会有多个，那我们的不动点是最精确的吗？
- 什么时候算法可以达到不动点？
由此，我们需要学习单调性与不动点定理，非常重要
4.6 单调性与不动点定理⭐
4.6.1 单调性 Monotonicity
定义：如果对于 ∀ x, y ∈ L，x ⊑ y ⟹ f(x) ⊑ f(y)，函数 f：L->L (L是一个格)是单调的。
4.6.2 不动点定理 Fixed-Point Theorem
定义：对于全格 (L, ⊑)，如果
1）f: L->L是单调的
2）L是有限的，
则 f 的最小不动点(least fixed point)可以通过迭代f(⊥), f(f(⊥)), …, (⊥) 来获得。
最大不动点(greatest fixed point)可以通过迭代f(T), f(f(T)), …, (T) 来获得。
注意：对于 may analysis ，它是从 bottom 向 top 变化的，不动点原理告诉我们从 ⊥ 出发不断的迭代函数 f ，最后得到的不动点是最小不动点，也就是最优的一个不动点。对于 may analysis ，它一定存在一个最大的不动点 T，在前面的示例中为 11111…111。must analysis 刚好相反，它一定存在一个最小的不动点 ⊥，在前面的示例中为 0000…000。
4.6.3 不动点定理的证明
这里，我们需要证明两点：
（1）不动点是存在的 （2）不动点是最小的
1. 不动点证明的存在性 Existence of Fixed Point
2. 不动点是最小的 Least Fixed Point
4.6.4 回顾之前提出的一些问题：
- 算法一定能停止或者一定可以达到不动点吗？或者说总有一个解吗？
——回忆“OUT never shrinks” ，这与单调性有关，会达到不动点
- 如果一定会停下，那会由多个不动点吗？如果会有多个，那我们的不动点是最精确的吗？
——对于一个函数来讲，只要满足 x = f(x) 即可称 x 为不动点，所以不动点并不唯一。目前我们知道的是根据不动点原理得到的不动点是最优的，但是并不不知道，迭代算法是否满足不动点定理。
- 什么时候算法可以达到不动点？
4.7 关联迭代算法与不动点定理
在上一小节中，我们证明了不动点定理，但是那是纯数学上的一个关于lattice中的函数的一个性质，是针对单个偏序集和单个传递函数的定理，对应到CFG中，就是针对单个节点（一个块B）的。因此我们不能直接说我们的迭代算法也有这个属性，除非我们能将算法与不动点定理关联起来。
本小节中，就是要将不动点定理与整个迭代算法关联起来，或者说将其与整个数据流分析关联起来。
1. 关联已知条件
如下图所示，我们将迭代算法与不动点定理的已知条件关联起来。
绿色部分的意思是：
- 每一个节点就对应一个lattice，整个CFG的域就是product lattice，又因为product lattice也是lattice，所以，整个CFG的域也是一个lattice，
- 并且如果构成L的是一系列complete lattice(全格)的乘积，那么L也是complete(and finite)，所以整个CFG的域的lattice 也是finite的
红色部分：
- 在每次迭代中，我们所应用的行为定义为一个函数 function F ，可以包含两个部分：
- (1) 转换函数transfer function
for every nodes
- (2) 每次控制流汇合的 join/meet function。
- (1) 转换函数transfer function
- 接下来要证明的就是：这个function F 是单调的（monotonic）
- (1) 转换函数transfer function
- 在这个转换函数中，使用到的是 gen 和 kill 是单调的（这个函数设计的时候，本身就是单调的，因为经过操作，只会让某元素从0变成1 ，而不会从1变成0）
- (2) join/meet function ⊔/ ⊓ : L × L → L for control-flow confluence (这里将很多个L的合并操作看作一次，这里我们只需要证明这个二元关系的join或meet操作时单调的即可)
- 这里有一些很严谨的步骤来证明⊔是单调的，如下图所示
- 前三行是很容易理解的，利用偏序关系的传递性，得到y ⊔ z 是y的上界也是x的上界；
- 又因为 x ⊔ z 是x 和z 的最小上界，根据最小上界定义，可以得到x ⊔ z ⊑ y ⊔ z
- 这里有一些很严谨的步骤来证明⊔是单调的，如下图所示
- (1) 转换函数transfer function
2. 回顾提出的问题
由此，我们就可以回答前两个问题了，算法一定能够达到不动点，要么是最大不动点，且一定是best one，要么是最小不动点，要么是最小不动点（待会还会去系统地理解什么是best）
还剩下一个问题就是到底什么时候能够达到不动点，实际上是在探讨算法的复杂度，最次多少次迭代可以达到不动点。
3. 什么时候算法到达不动点？
如下图所示，lattice的从top到bottom的路径长度为高度h，假设CFG中的节点数为k，最坏情况下，每一步只改变了一个node里的一个0，则最坏情况下，需要迭代 i=h*k 次才能到达不动点。（其中高度h可以理解为有多少个需要分析的变量/定义等，也就是多少位字节表示。）
所以，这里就可以算出来最坏情况下的迭代次数，就是路径的长度与CFG中节点个数的乘积
4.8 从Lattice的视角看 May/ Must 分析⭐⭐
这节的图都非常重要，方便以后用到的时候查阅。
4.8.1 总体映射
首先将左侧的图，映射到右侧的椭圆中，假设我们设的这个格是我们之前所介绍的乘积格，但是我们仍把他当成一个格来处理
其实不管是must 还是may，都是从一个不安全的状态，一步步迭代，到达最安全的状态，只不过，不同的分析，起始可能不一样，具体分析如下。
4.8.2 MAY 分析
对于may analysis，目的是查错，bottom 就是初始的unsafe状态，也就是说，所有的都没错，这显然分析结果是不安全的，而top则是所有的都可能有错，这显然分析很安全，但是也没什么用。
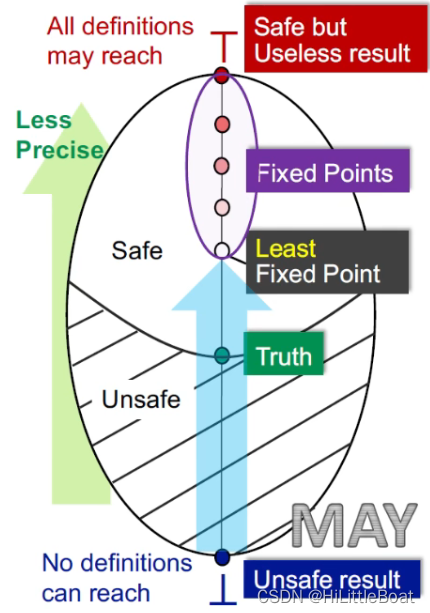
如下图所示，以可达性分析为例：
- bottom就是全0，意味着，所有的定义都不可达，这是一个不安全的结论，（因为这个分析的应用目的是为了查错，查看变量是否需要初始化。首先在Entry中给每个变量一个假定义，标记所有变量为都为未初始化状态，bottom表示所有的假定义都无法到达，说明所有变量在中间都进行了赋值，那就不需要对任何变量进行初始化，这是不安全的，可能导致未初始化错误）
- top就是all dummy definition may reach。从查错角度来说，需要对每个变量都进行初始化，这显然非常安全，但是没有什么用！
- Truth代表最准确的验证结果，假设{a,c}是truth，那么包括其以上的都是safe的，以下的都是unsafe，如图中的阴影和非阴影。
所以，对于may analysis而言，从unsafe → safe 的路径就是从 bottom → top。因为函数是单调的，所以经过一次次迭代，算法会停在safe中最接近truth的不动点，即最小不动点（Least Fixed Point）。
4.8.3 MUST 分析
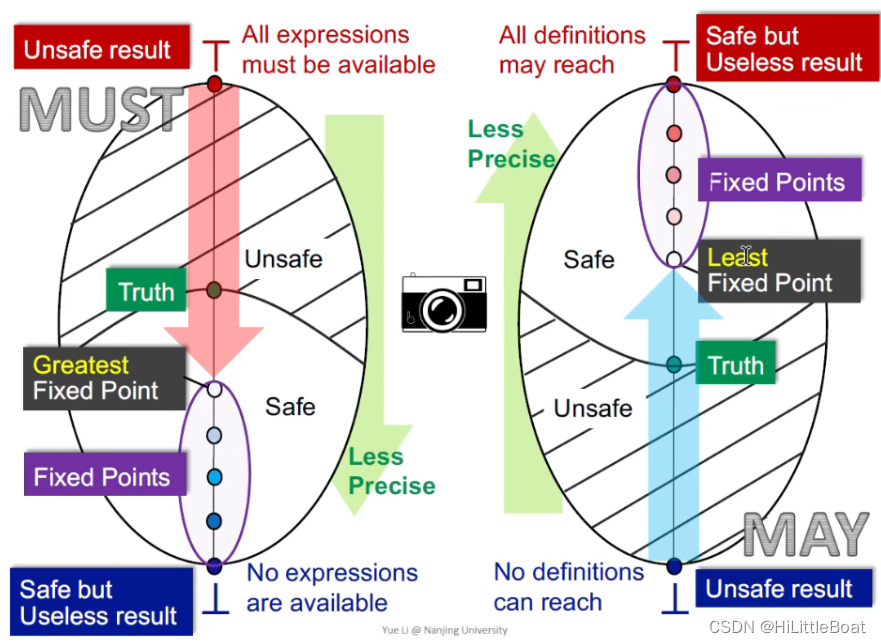
对于must analysis，目的是优化，top是初始的unsafe状态，意味着所有的都能优化，这显然不安全，bottom 则是safe的，也就是说，所有的都不能被优化，这显然分析很安全，但是也没什么用。
所以，对于must analysis而言，从unsafe → safe 的路径就是从top→ bottom 。因为函数是单调的，所以经过一次次迭代，算法会停在safe中最接近truth的不动点，即最大不动点（Greatest Fixed Point）。
4.8.4 精华图，截图保存⭐
4.9 Distributivity(分配性) and MOP
我们前边提到了精度，但是我们的精度到底怎么样？谈到分析精度，这里介绍一些很经典的概念，Meet-Over-All-Paths Solution(MOP)，可以用来衡量迭代算法的精度
4.9.1 MOP的基本概念
目的：衡量迭代算法的精度
概念：Meet-Over-All-Paths Solution(MOP)，就是所有路径在汇聚到一点的时候，把结果meet或join（meet是用来求最大下届，join是求最小上界，名字中只用meet 来代表 meet 和join 两种合并操作）
具体来看，如下图所示：
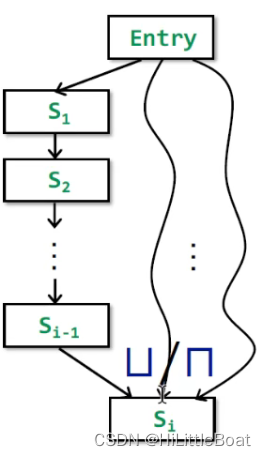
这里有几个概念：
- 路径P： 代表CFG上，从Entry到Si 节点的一条路径
- 路径P上的转换函数Fp： 代表路径P上所有语句的转移函数的组合fs1，fs2，... ，fsi-1，从而构成Fp
- MOP[si]：表示从Entry节点到Si节点上的所有路径P应用转换函数Fp之后再进行meet操作（控制流处理）。本质是求这些值的最小上界/最大下界。
MOP计算每个路径末端的数据流值，并对这些值应用join/meet运算符，以找到它们的lub/glb。（lub是最小上界，glb是最大下界，详见4.3）。
MOP准确性：
- 实际上，有些路径可能不会被执行，在某些路径不执行的情况下仍进行控制流处理是不精确的，not executable → not fully precise
- 若路径包含循环，或者路径爆炸，所以实操性不高，只能作为理论的一种衡量方式。
not enumberable → impractical
4.9.2 Ours(迭代算法) vs. MOP
如下图所示，我们的方法是在所有的merge的地方，都进行控制流合并操作，但是MOP是在路径算完之后，对每条路径进行merge。
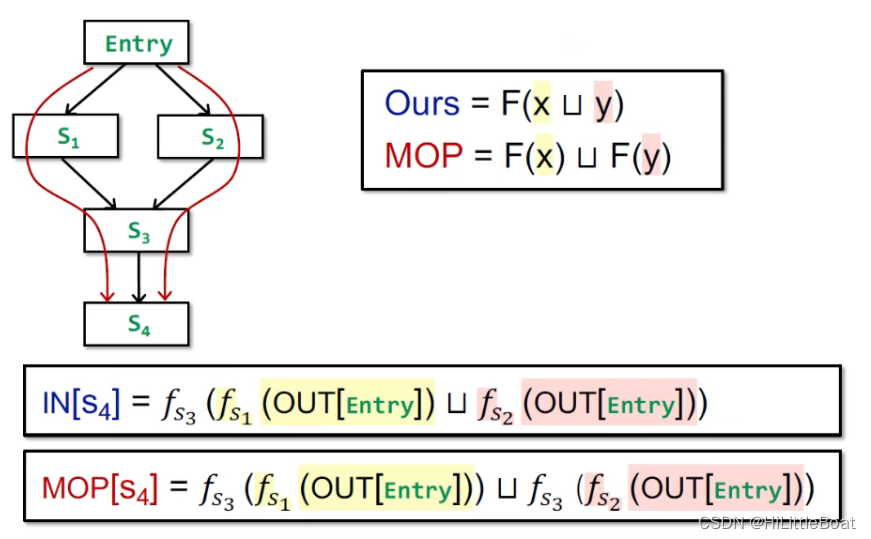
观察这两种方法，可以找到两部分相同的元素，黄色部分用x代替，红色部分用y代替。可以抽象出两种方法的结论，如图右上方所示。接下来，我们将分析两者之间的关系。
如上图所示，是迭代算法与MOP精度的比较，具体解释如下：
证明部分：
-
根据最小上界的定义，有x⊑x⊔y和 y⊑x⊔y。
-
由于转换函数F是单调的，则有F(x)⊑F(x⊔y)和F(y)⊑F(x⊔y)，所以F(x⊔y)就是F(x)和F(y)的上界。
-
根据定义，F(x)⊔F(y)是F(x)和F(y)的最小上界。
-
所以F(x)⊔F(y)⊑F(x⊔y)
结论：
- MOP的精度比迭代算法更高一些。
- 当转换函数F是distributive（可分配）的时候，F(x)⊔F(y)=F(x⊔y)，MOP=Ours，我们的方法与MOP一样精确
前边讲的那些 Bit-vector or gen/kill problems（可以用join/meet，是进行集合的交或并操作的），都满足分配律distributive。
但是也存在一些转换函数，不是distributive的，见4.10
4.10 Constant Propagation 常量传播
1. 定义
Given a variable x at program point p, determine whether x is guaranteed to hold a constant value at p. 在程序点p处给定一个变量x，确定x是否能保证在p处保持是一个常量。
根据定义，有强调“保证，一定”的意味，所以是must分析，是要考虑经过p点所有的路径上，x的值都必须是一样的，才算是保持常量。
这里的CFG中每个节点的OUT是比较特殊的，包含了一对值(x, v)，其中x代表一个变量（名），v是x经过这个节点之后的值
2. 组成
在4.5 中讲到，数据流分析主要由三个部分组成(D, L, F)
- D: 数据流的方向(direction)：forwards 或 backwards
- L: 包含值域V 和 一个meet ⊓ 或 join ⊔ 操作符的格(lattice)
- F: 一系列值域V到V的转换函数(transfer funtion)
所以我们依照这个思路，首先确定一下改数据流分析主要的组成.
（1）方向(direction, D)
因为我们最开始我们并不知道各种情况，我们想知道某个点，过去发生了什么，需要往前看，所以可以确定D(direction)为forwards，正向。
（2）格(lattice， L)
- V的值域
先确定lattice，可以看到变量的取值是所有实数都可以，并且是must分析，其方向是从top(unsafe)→bottom(safe)，所以top定义的是undefined（所有变量都未定义）；bottom就是NAC（就是所有变量都是非常量），如下图所示。
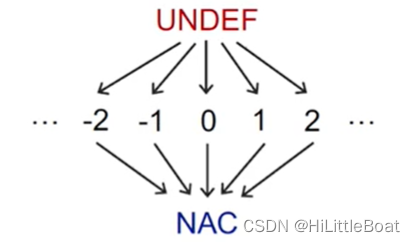
这里的top定义为undefined “所有的变量都未定义” ，而不是定义成 “所有变量都是常数” ，是因为前边曾说到，这里的值是比较特殊的，是一对值(x,v)，我们在初始化的时候，程序还没有运行起来，所以将初始值定义为undefined。
- meet操作符⊓
再确定meet，在控制流合并的时候，不同的路径如何combine？因为是must-analysis，所以是⊓，可能会出现如下情况：（所以不是常见的交和并）
◆ NAC ⊓ v = NAC
◆ UNDEF ⊓ v = v //未初始化的变量不是我们分析的目标，这里不考虑未定义的变量被忽略
◆ c ⊓ v = ? c ⊓ c = c; c1 ⊓ c2 =NAC
在每个路径汇聚点PC上，我们应该对该PC上流入的所有变量进行meet操作，但并非常见的交和并，所以不满足分配律。
（3）转换函数(transfer funtion, F)
转换函数定义如下：（和之前遇到的迭代算法类似）
意思是输入的减去BB中相关变量值已经不是f常量的部分；并上在BB中新被赋值的。 其中，s 为一个语句：x=... 我们使用val(x) 表示变量x所持有的lattice值)。
接下来，分析将所有可能遇到赋值的语句，具体情况如下图所示： 
注意，如果不是赋值语句，就没影响。
3. 为什么是Nondistributivity
4.11 Worklist 算法，一种迭代算法的优化（更常用）
1. 回顾迭代算法
如上图所示，是之前我们学到的算法，算法停下来的要求是，所有的OUT都不再发生改变，但是每次都需要对所有已经不变的在遍历一次。
worklist算法的核心就是将有变化的值挑出来，再去利用转换函数和控制流操作。
2. Worklist 算法 
🦄总结:
终于搞定了这两节课，其中4.8里的图是非常重要的，值得后续反复观看，也需要自己能画出来。理解不动点定理、MOP与迭代算法的精度。尝试完成一下constant propagation analysis的实验，通过迭代算法和worklist算法。
🦄写在后边:
上个月期末考试+外出，进度慢了些。这几节课还挺难的，幸好还是坚持下来了，希望这个月内能够把这个课程学完，欢迎各位小伙伴一起学习交流。
老师的PPT真的做的非常精细，很多时候写出来自己的理解（翻译），还是想贴出来老师的ppt，有的时候会将自己的理解进行批注，有不正确的地方，欢迎交流。
也希望能够做到像老师所说的，在面对未来的工作时，能够更加自信，处理起来更加从容！
其他的写的很好的博主的文章：
软件分析——数据流分析2_zcc今天好好学习了吗的博客-CSDN博客
【课程笔记】南大软件分析课程4——数据流分析基础（课时5/6） - 简书
【软件分析/静态程序分析学习笔记】5.数据流分析基础(Data Flow Analysis-Foundations)_may analyses must analyses_童年梦的博客-CSDN博客
扫一扫
3813
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
