前言
本节将介绍线性代数中的基本数学对象、算术和运算,并用数学符号和相应的代码实现来表示它们。
线性代数
以下为线性代数的基本知识,不作过多阐述。

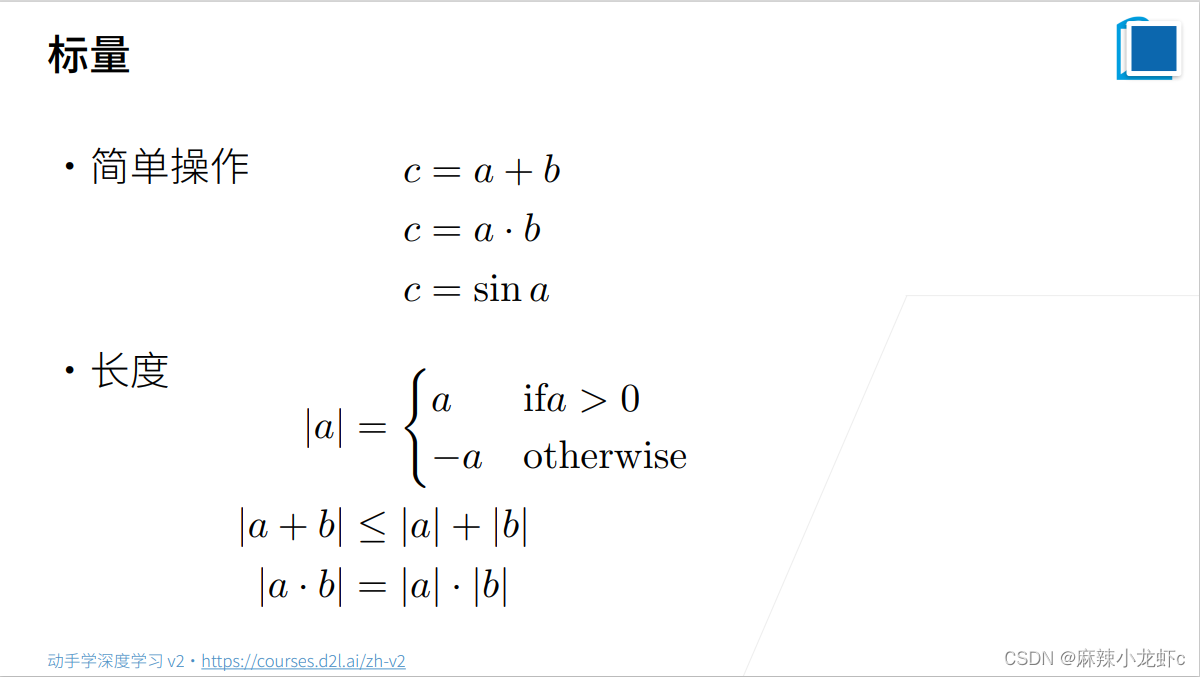



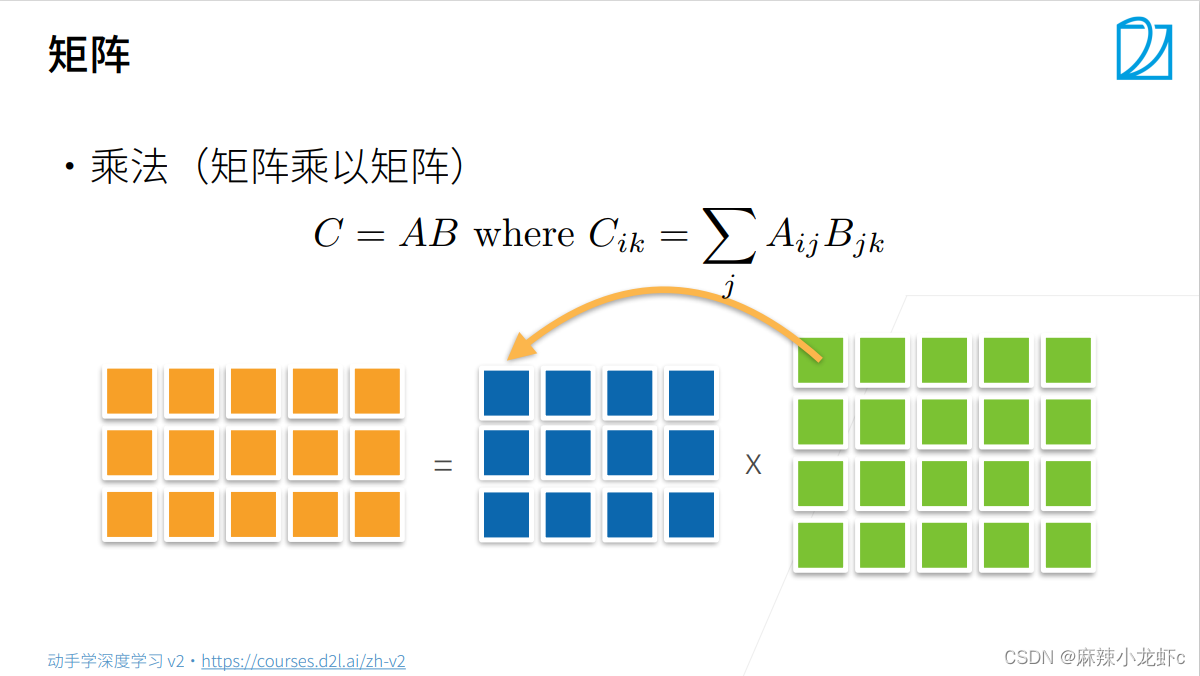



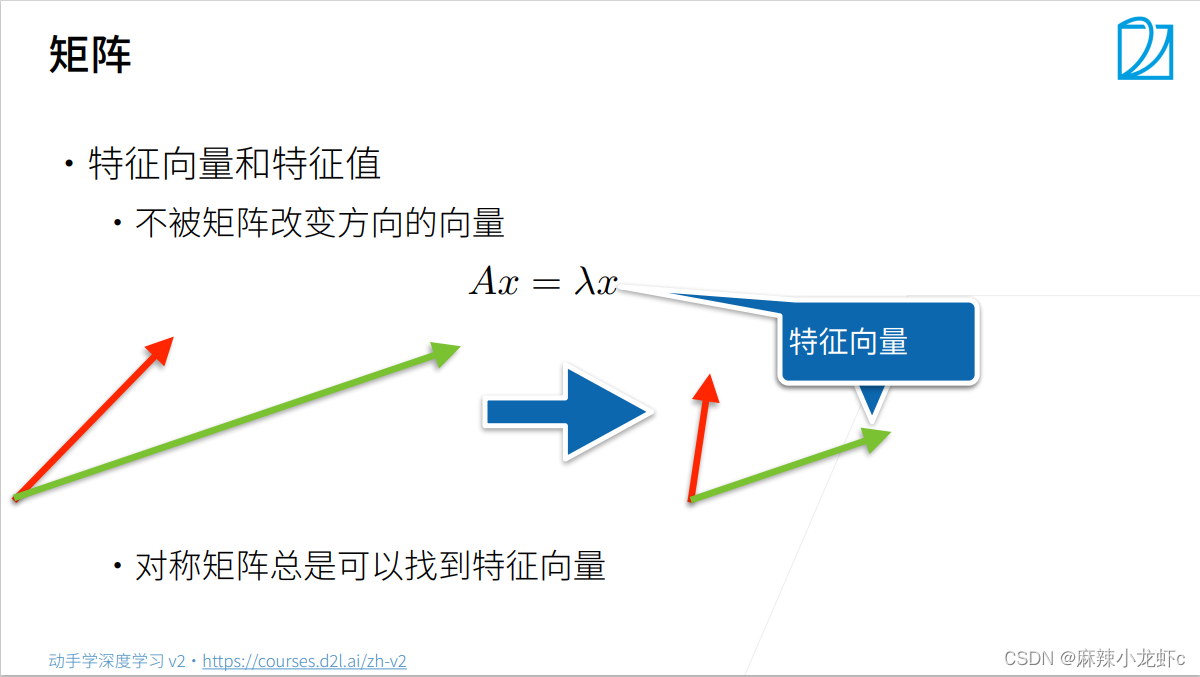
线性代数实现
标量
标量由只有一个元素的张量表示。 下面的代码将实例化两个标量,并执行一些熟悉的算术运算,即加法、乘法、除法和指数。

()内直接是数字,没有[],表示是一个0维的张量,也就是向量。
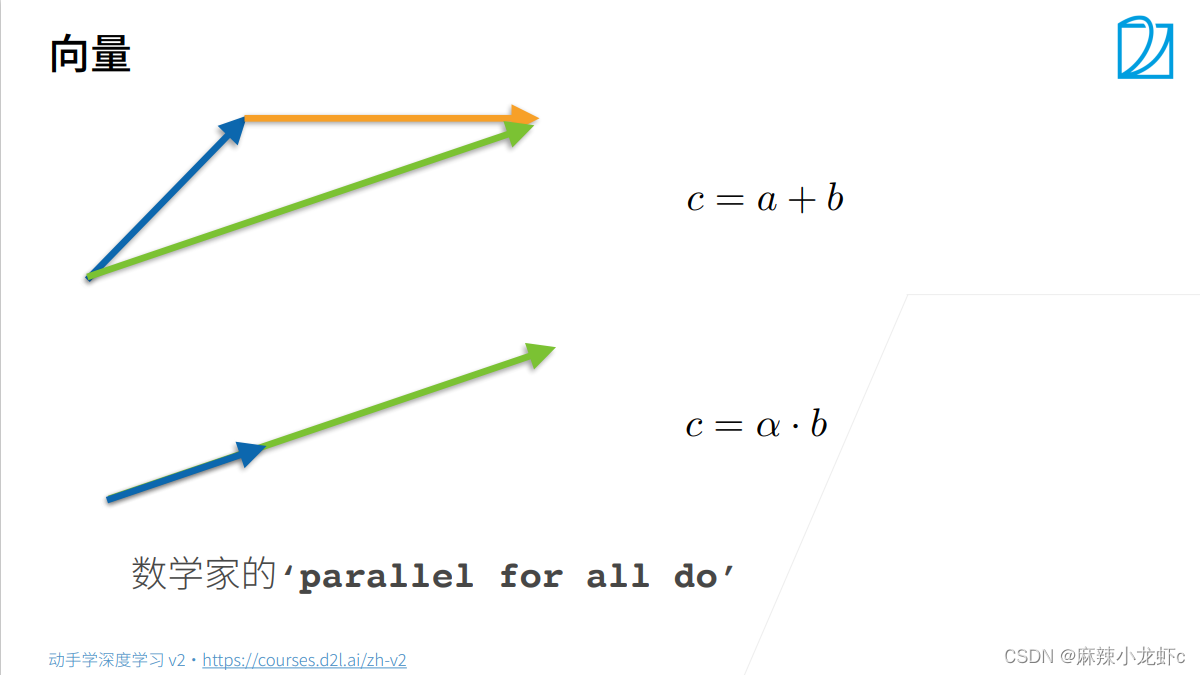
向量
人们通过一维张量表示向量。一般来说,张量可以具有任意长度,取决于机器的内存限制。



长度、维度和形状
向量只是一个数字数组,就像每个数组都有一个长度一样,每个向量也是如此。
与普通的Python数组一样,我们可以通过调用Python的内置len()函数来访问张量的长度。

当用张量表示一个向量(只有一个轴)时,我们也可以通过.shape属性访问向量的长度。 形状(shape)是一个元素组,列出了张量沿每个轴的长度(维数)。 对于只有一个轴的张量,形状只有一个元素。
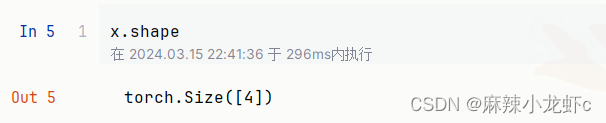
请注意,维度(dimension)这个词在不同上下文时往往会有不同的含义,这经常会使人感到困惑。 为了清楚起见,我们在此明确一下: 向量或轴的维度被用来表示向量或轴的长度,即向量或轴的元素数量。 然而,张量的维度用来表示张量具有的轴数。 在这个意义上,张量的某个轴的维数就是这个轴的长度。
矩阵

当调用函数来实例化张量时, 我们可以通过指定两个分量m和n来创建一个形状为m × n的矩阵。



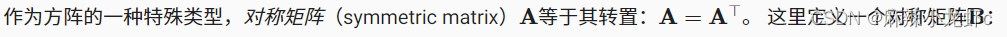

现在我们将B与它的转置进行比较。

张量
当我们开始处理图像时,张量将变得更加重要,图像以n维数组形式出现, 其中3个轴对应于高度、宽度,以及一个通道(channel)轴, 用于表示颜色通道(红色、绿色和蓝色)。 现在先将高阶张量暂放一边,而是专注学习其基础知识。

张量算法的基本性质
标量、向量、矩阵和任意数量轴的张量(本小节中的“张量”指代数对象)有一些实用的属性。 例如,从按元素操作的定义中可以注意到,任何按元素的一元运算都不会改变其操作数的形状。 同样,给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。 例如,将两个相同形状的矩阵相加,会在这两个矩阵上执行元素加法。
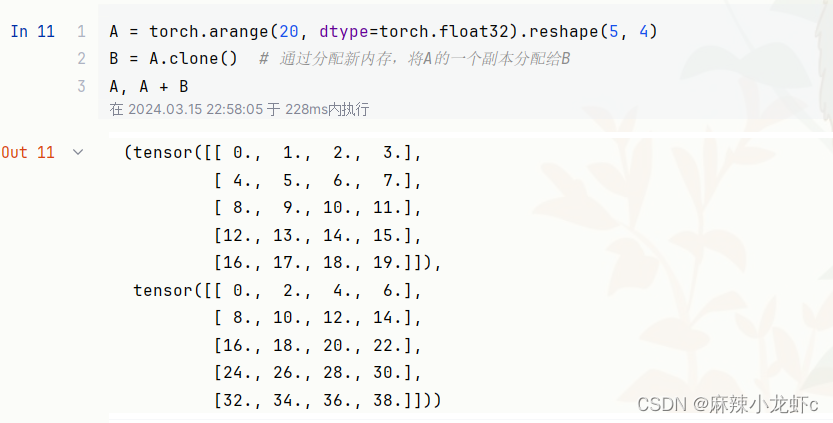


将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘。

降维
我们可以对任意张量进行的一个有用的操作是计算其元素的和。

我们可以表示任意形状张量的元素和。

默认情况下,调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。 我们还可以指定张量沿哪一个轴来通过求和降低维度。 以矩阵为例,为了通过求和所有行的元素来降维(轴0),可以在调用函数时指定axis=0。 由于输入矩阵沿0轴降维以生成输出向量,因此输入轴0的维数在输出形状中消失。

指定axis=1将通过汇总所有列的元素降维(轴1)。因此,输入轴1的维数在输出形状中消失。

沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和。

一个与求和相关的量是平均值(mean或average)。 我们通过将总和除以元素总数来计算平均值。 在代码中,我们可以调用函数来计算任意形状张量的平均值。

同样,计算平均值的函数也可以沿指定轴降低张量的维度。

非降维求和
但是,有时在调用函数来计算总和或均值时保持轴数不变会很有用。
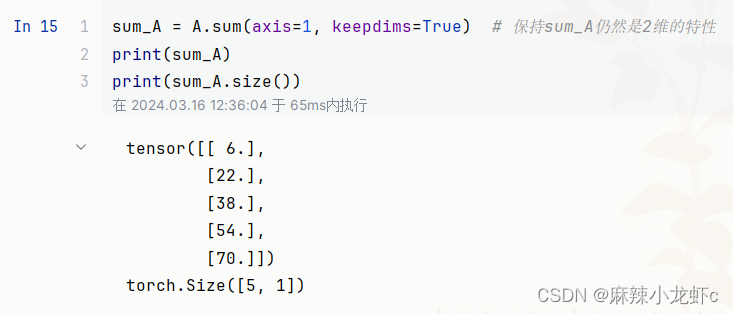
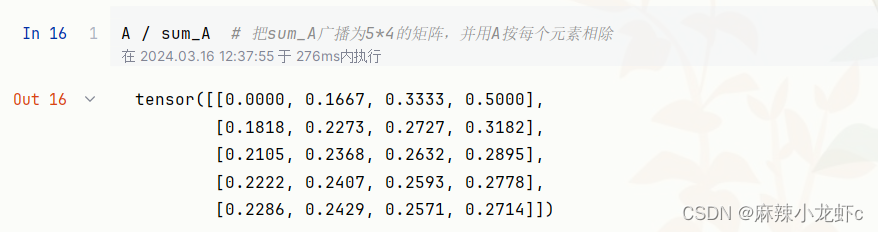
例如,由于sum_A在对每行进行求和后仍保持两个轴(注意这里axis=1实际是按列求和,但理解起来是对每行进行求和),我们可以通过广播将A除以sum_A。
如果我们想沿某个轴计算A元素的累积总和, 比如axis=0(按行计算),可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

点积(Dot Product)


注意,我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积:


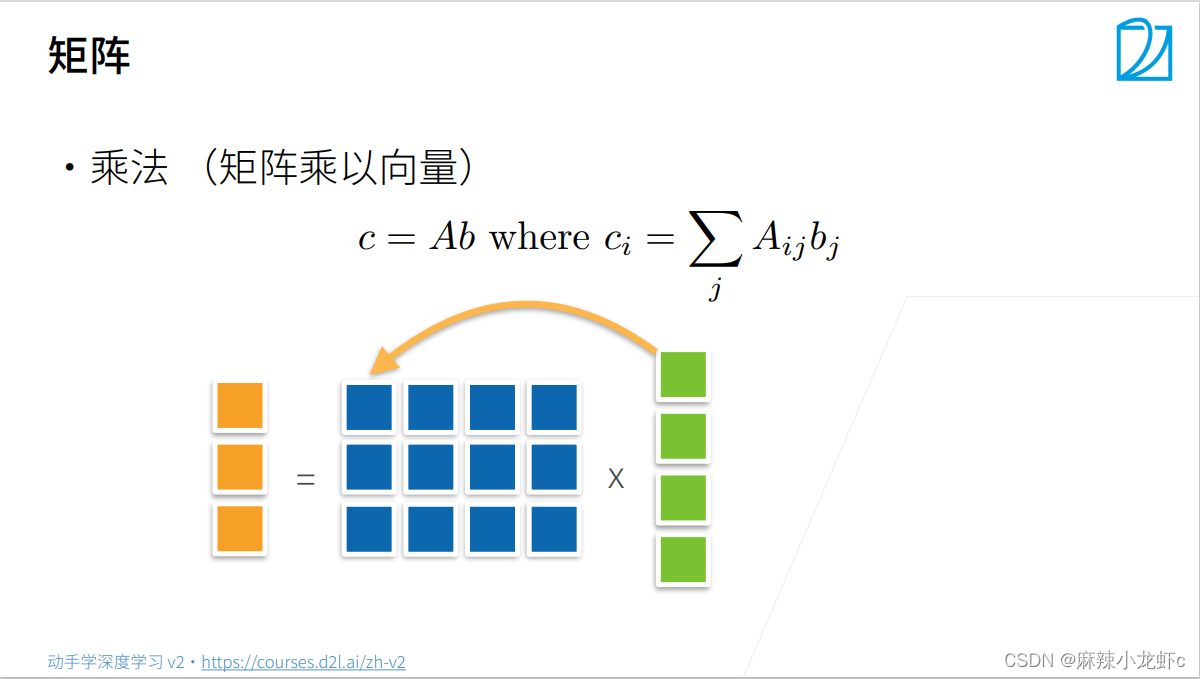
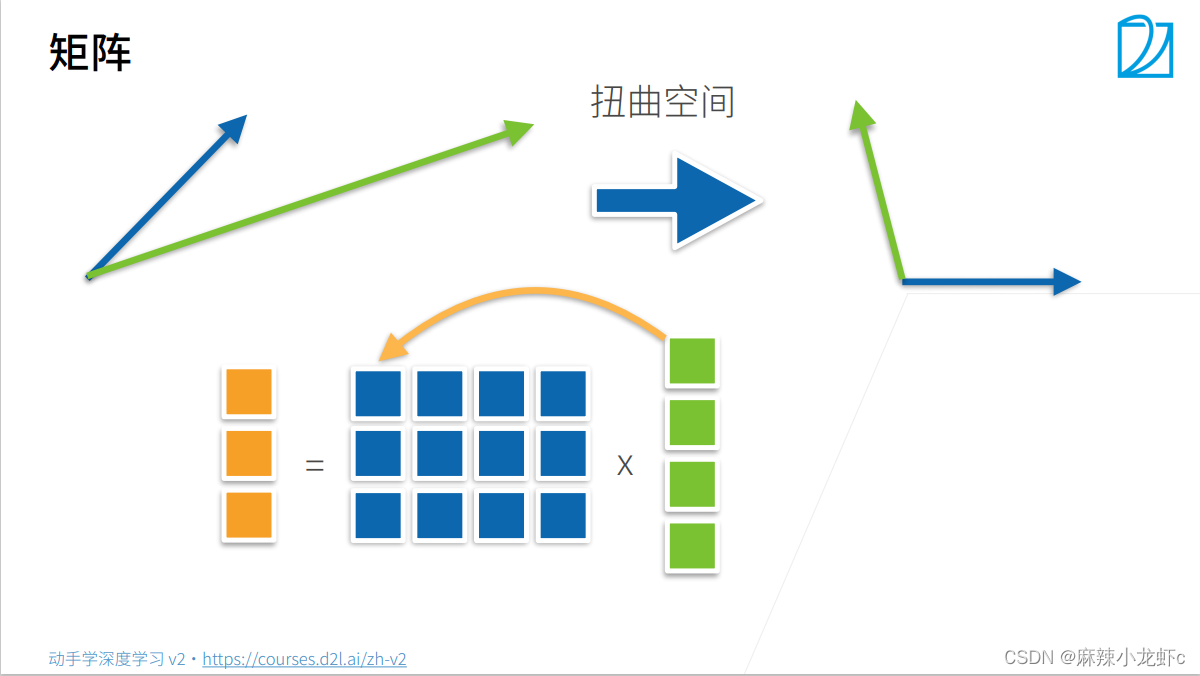
矩阵-向量积
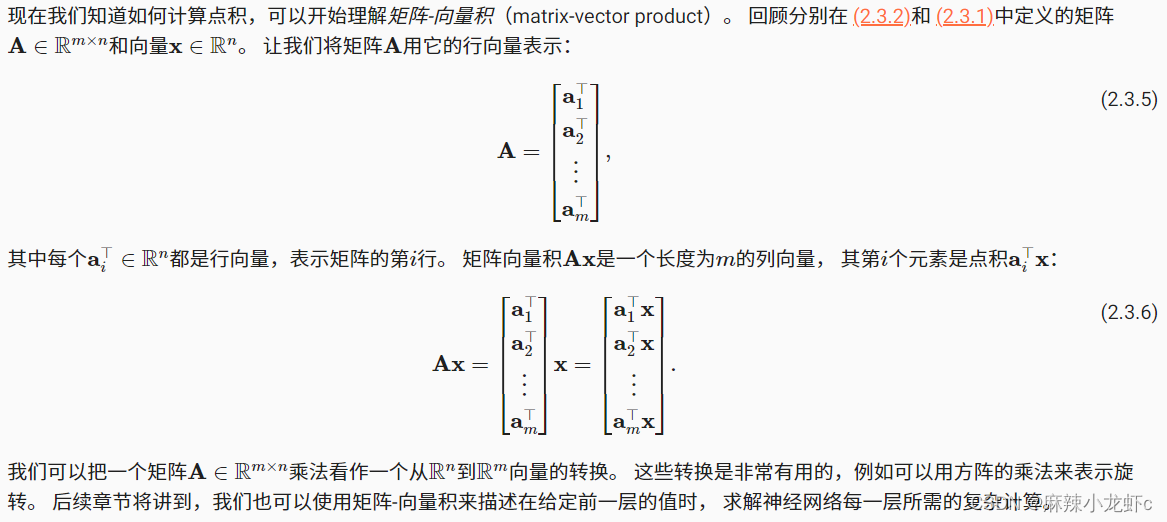
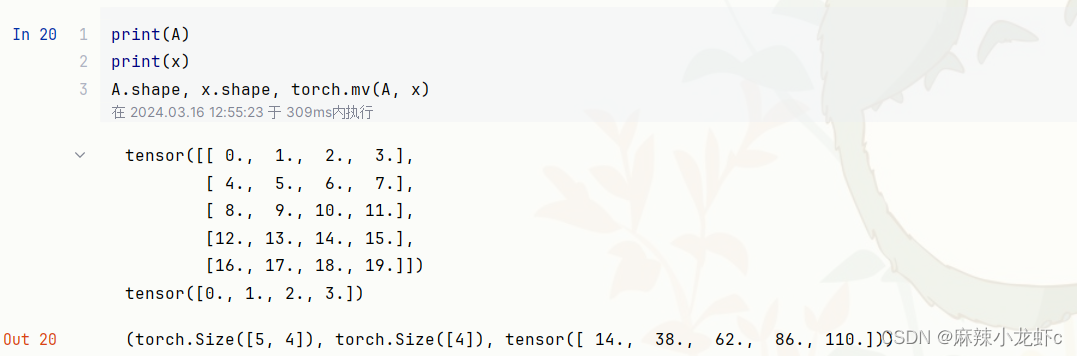
在代码中使用张量表示矩阵-向量积,我们使用mv函数。 当我们为矩阵A和向量x调用torch.mv(A, x)时,会执行矩阵-向量积。 注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
矩阵-矩阵乘法

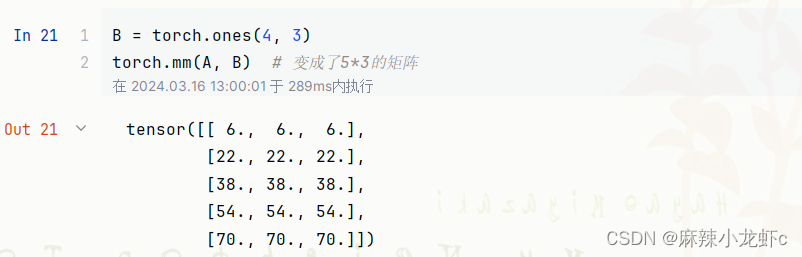
矩阵-矩阵乘法可以简单地称为矩阵乘法,不应与“Hadamard积”混淆。
范数






小结
- 标量、向量、矩阵和张量是线性代数中的基本数学对象。
- 向量泛化自标量,矩阵泛化自向量。
- 标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴。
- 一个张量可以通过sum和mean沿指定的轴降低维度。
- 两个矩阵的按元素乘法被称为他们的Hadamard积。它与矩阵乘法不同。
- 在深度学习中,我们经常使用范数,如第一范数、第二范数和Frobenius范数。
- 我们可以对标量、向量、矩阵和张量执行各种操作。
练习

前三个证明不作过多阐述,直接从问题四开始。

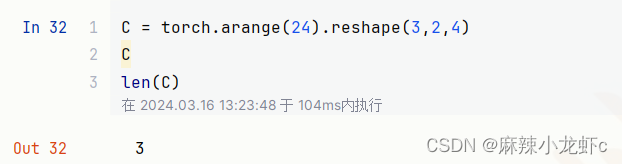
可以发现长度是第一个维度——0维度的长度
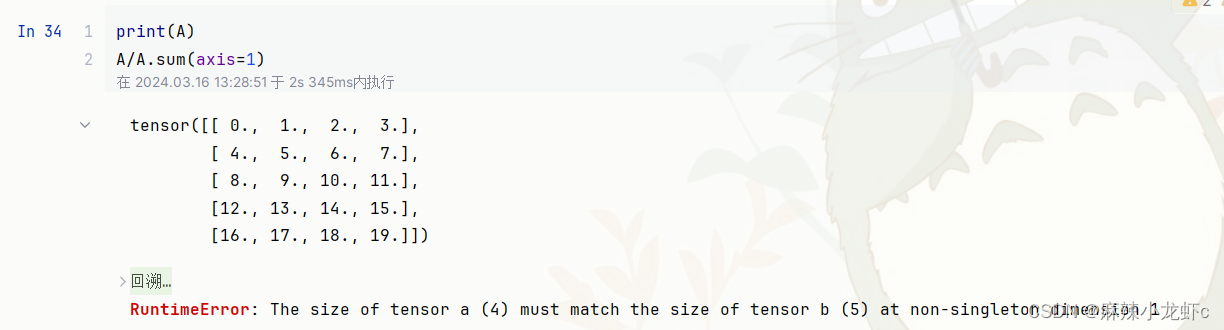
无法相除,原因是因为A.sum(axis=1)求出来的是一个形状为[5]的张量,维度变成了一维,无法做广播。
当保留维度后就可以做广播机制,也就可以相除了

下面详细叙述以下按固定轴求和

求和后的值是一个标量,注意这里的标量值的是张量中的0维标量,实际上还是一个张量

可以看到,按维度1求和后,维度1上的5直接被压缩,形状由254的三维张量变成了2*4的二维张量

同理,按0维度求和,则0维度上的2直接被压缩,变成了5*4的张量。这里可以发现一个规律,按哪个维度求和,最终的值是按照维度上的值来计算的(比如5和2)

也可以批量设置维度,可以看到0维度和2维度都被压缩,最终变成了长度为5的向量,这里值都变成了8,可以理解成先按照维度0的数值2相加成2,再按照维度2的数值4相加得到8。

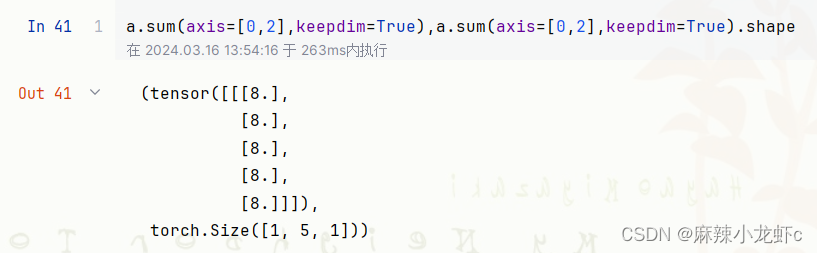
当保留维度后,原本的维度不变——还是一个三维张量,但是形状变了,数值仍然是8不变。这种处理可以做广播,方便后续处理。






















 786
786











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








