python求解经典汉诺塔问题、多塔汉诺塔问题

一、经典汉诺塔

汉诺塔是根据一个传说形成的数学问题：
有三根杆子A，B，C。A杆上有 N 个 (N>1) 穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆：
1、每次只能移动一个圆盘；
2、大盘不能叠在小盘上面。
问：如何移？最少要移动多少次？

1、基本想法

用$f(n,A,B)$来表示把n个圆盘从A移到B的方法；
ABC三根杆子，B作为缓存区，n个圆盘从A到C。
分为三步：
1、先把n-1个盘从A移到B，$f(n-1,A,B)$
2、再把第n个圆盘从A移到C，$f(1,A,C)$
3、最后把之前移到B的圆盘从B移到C，$f(n-1,B,C)$
得到$f(n,A,C)=f(n-1,A,B)+f(1,A,C)+f(n-1,B,C)$

2、python实现

def f(s,from_,to_,trans_): #输入一个圆盘list，从哪（from_）移到哪（to_），缓存区是哪个（trans_）
	if len(s) == 1:
		return [tuple([s[0],from_,to_])]  #一次移动用元组表示
	else:
		method = f(s[:-1],from_,trans_,to_)+\
		f([s[-1]],from_,to_,trans_)+\
		f(s[:-1],trans_,to_,from_)
		return method   #最后的方法储存在列表里
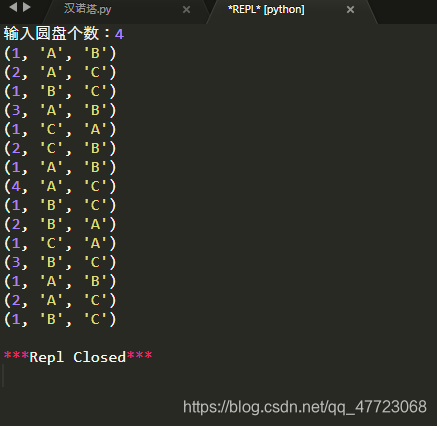
def main():
	n = int(input('输入圆盘个数：'))
	s = [i+1 for i in range(n)]
	for j in f(s,'A','C','B'):
		print(j)
main()

运行结果示例：

3、伪可视化

from time import sleep

def f(s,from_,to_,trans_):
	if len(s) == 1:
		return [tuple([s[0],from_,to_])]
	else:
		#注意，f的第一个参数必须是列表
		method = f(s[:-1],from_,trans_,to_)+\
		f([s[-1]],from_,to_,trans_)+\
		f(s[:-1],trans_,to_,from_)
		return method
def pr(n,A,B,C):
	A_,B_,C_ = A[:],B[:],C[:] #副本，不要直接修改A，B，C
	for i in (A_,B_,C_,):
		if len(i) < n:
			for j in range(n-len(i)):
				i.insert(0,'*') #不足n个圆盘的柱子用*填满
	for j in range(n):
		print('{}\t{}\t{}'.format(A_[j],B_[j],C_[j])) #格式化输出一下
def show(n,method,A,B,C):
	pr(n,A,B,C)
	count = 1
	for i in method:
		print('——————————————\n这是第%d次移动：'%count)
		sleep(0.5)
		eval(i[1]).remove(i[0])  #只有一个元素所以可以用remove：（remove删去第一个匹配项）
		eval(i[2]).insert(0,i[0])  #放在最上面，不同append
		pr(n,A,B,C)
		count +=1
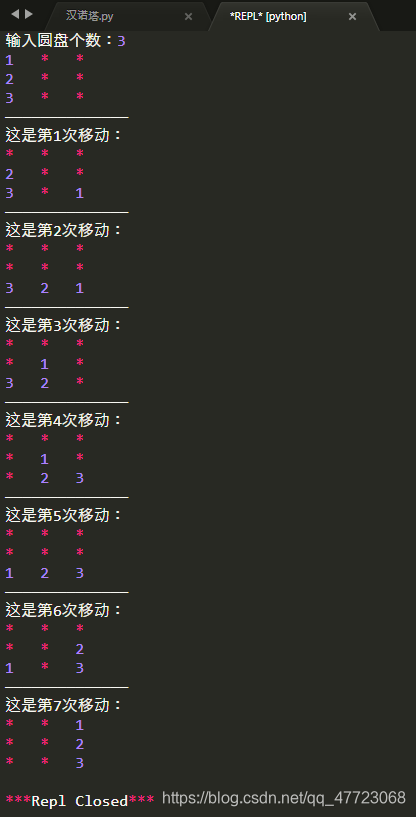
def main():
	n = int(input('输入圆盘个数：'))
	s = [i+1 for i in range(n)]
	method = f(s,'A','C','B')
	A = [i+1 for i in range(n)]
	B = []
	C = []
	show(n,method,A,B,C)
main()

运行结果示例：

二、多个柱子的汉诺塔

1、算法：

（来自WIKI百科）
Frame-Stewart 演算法本质上上也是递归的，可简答敘述如下：
令$f(n,k)$为在有$k$个柱子时，移动n个圆盘到另一柱子上至少需要的步数，则：
对于任何移动方法，必定会先将$m(1\le m\le n-1)$个圆盘移动到一个中间柱子上，再将第 $n$到第 $n-m$个圆盘通过剩下的$k-1$个柱子移到目标柱子上，最后将$m$个在中间柱子上的圆盘移动到目标柱子上。这样所需的操作步数为$2f(m,k)+f(n-m,k-1)$。
进行最优化，易得:$f(n,k)={min}_{m\in [1,n-1]}(2f(m,k)+f(n-m,k-1))$。
显然这里有$$f(n,2)=\{\begin{array}{ll}1& \text{if n=1}\\ \infty & \text{else}\end{array}$$

2、如何理解上面的必定？

首先任何一种移动方法，必然会$m(1\le m\le n-1)$个移到一个柱子上；
$m=1$很好理解，视为这一步只移动了一个；
$1\le m\le n-1$，则理解为把m个圆盘按照大小顺序移到另外一个柱子，形如

变到

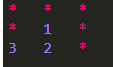
这两种都满足$f(n,k)$
然后剩下$n-m$个圆盘，先移动的都是较小的圆盘，故而剩下的$n-m$个较大的圆盘就只能移动到其余的$k-1$个柱子上，也就是递归到了在有$k$个柱子的情况下把$n-m$个圆盘移到目标柱子的问题。

3、python递归求解次数

数学推导递归出口：
$n=1$时，$f(1,k)=1$
$k=3$时，
$$\begin{gathered} f(n,3) \\ ={min}_{m\in [1,n-1]}(2f(m,3)+f(n-m,2)) \\ （这里注意到f(n,2)=\infty :ifn>1） \\ =2f(n-1,3)+f(1,2) \\ =2f(n-1,3)+1 \\ =2^{2}f(n-2,3)+2+1 \\ =\dots \dots \\ =2^{n-1}f(1,3)+{\sum }_{k=0}^{n-2}{2}^k \\ =2^n-1 \end{gathered}$$

def f(n,k):
    if  n == 1:#关于n的递归出口
        return 1
    elif k == 3:#关于k的递归出口
        return pow(2,n)-1
    else:
        F = min([2*f(m,k)+f(n-m,k-1) for m in range(1,n)])
        return F
for i in range(1,13):
    for j in range(3,15):
        print('f({},{})={}'.format(i,j,f(i,j)))

运行结果示例：
可以看到$f(n,k)$随着$k$的增大最终收敛于$2n-1$
实际上很容易知道，$k\ge n-1$时$f(n,k)=2n-1$,此时的最少移动次数方法为把所有的圆盘依次分别放到不同的柱子上再依次移到目标柱子上。

3、递推求解移动步骤（在时间复杂度上，递归显然不如递推，不过递推的空间复杂度更高）

def 

待续