【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】模型选择

模型选择是机器学习中比较重要的问题，选择的不同的模型会造成不同的后果：

• 拟合能力强的模型一般复杂度较高，容易过拟合
• 如果限制模型复杂度，降低拟合能力，可能会欠拟合
  在模型训练的过程中越复杂的模型对应的训练错误率越低，但是并不能以训练时的错误率去评判模型的优劣，要用与训练过程无关的测试集来判断，这也就意味着在选择模型时，测试集不可见。那么在训练时，要如何判断哪个模型更优秀呢？为此，需要引入验证集（Validation Set或Development Set）。
  验证集可以是单独的数据集，也可以从原训练集中选择部分作为验证集。当使用不同的模型在训练集上完成训练后，接着验证模型在验证集上的错误率，以此来评价哪个模型更优秀。
  但是当训练集数据很少时，如果再从中拿出足够量的训练集，就会加剧数据稀疏问题。为此，可以通过交叉验证（Cross-Validation） 方式来尽可能的使验证集与训练集比例相当，尽可能提高数据利用率。
  所谓交叉验证就是指将训练集分为S组，每次使用S-1组作为训练集，剩下一组作为验证集。然后最终选择验证集上平均性能最好的一组作为最后的模型。
  

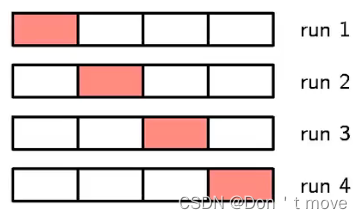
如上图将训练集分为4组，每次选择3组作为训练集、剩下1组作为验证集。

除了上面所说通过验证集来进行模型选择之外，还可以在一些准则的指导下进行模型选择，常用的准则有：

• 赤池信息量准则（Akaike Information Criterion，AIC）
• 贝叶斯信息准则（Bayesian Information Criterion，BIC）¹

偏差-方差分解（Bais-Variance Decomposition）

模型选择的实质是在期望风险与模型复杂度之间做平衡，二者之间的关系可以从期望风险入手，将期望风险分为方差（Variance） 和偏差（Bais） 来进一步解释期望风险与模型复杂度的关系。
仍然以线性回归为例，设当前选择的模型为$f(x)$，损失函数仍然是平方损失函数，则对应的经验风险为
$$\begin{array}{rl}\mathcal{R}(f)& ={\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(y-f(x){)}^2]\\ & =(y-f(x){)}^{2}p(x,y)\\ & =(y-f(x){)}^{2}p(x)p(y\mid x)\\ & =((y-f(x){)}^{2}p(y\mid x))p(x)\\ & ={\mathbb{E}}_{y\sim p_r(y\mid x)}[(y-f(x){)}^2]p(x)\\ & ={\mathbb{E}}_{x\sim p_r(x)}[{\mathbb{E}}_{y\sim p_r(y\mid x)}[(y-f(x){)}^2]]\end{array}$$
下面为了方便看，把${\mathbb{E}}_{x\sim p_r(x)}$简写成${\mathbb{E}}_x$，把${\mathbb{E}}_{y\sim p_r(y\mid x)}$简写成${\mathbb{E}}_y$，另外把$y$ given $x$下$y$的期望记作$\mu (x)$也即$\mu (x)={\mathbb{E}}_{y\sim p_r(y\mid x)}[y]$ 。

$$\begin{array}{rl}\mathcal{R}(f)& ={\mathbb{E}}_x[{\mathbb{E}}_y[(y-f(x){)}^2]]\\ & ={\mathbb{E}}_x[{\mathbb{E}}_y[(y-\mu (x)+\mu (x)-f(x){)}^2]]\\ & ={\mathbb{E}}_x[{\mathbb{E}}_y[(y-\mu (x){)}^2+(\mu (x)-f(x){)}^2+2(\mu (x)-f(x))(y-\mu (x))]]\\ & ={\mathbb{E}}_x[{\mathbb{E}}_y[(y-\mu (x){)}^2+(\mu (x)-f(x){)}^2]+2(\mu (x)-f(x)){\mathbb{E}}_y[(y-\mu (x))]]\\ & ={\mathbb{E}}_x[{\mathbb{E}}_y[(y-\mu (x){)}^2+(\mu (x)-f(x){)}^2]+2(\mu (x)-f(x))({\mathbb{E}}_y[y]-{\mathbb{E}}_y[\mu (x)])]\\ & ={\mathbb{E}}_x[{\mathbb{E}}_y[(y-\mu (x){)}^2+(\mu (x)-f(x){)}^2]+2(\mu (x)-f(x))(\mu (x)-\mu (x))]\\ & ={\mathbb{E}}_x[{\mathbb{E}}_y[(y-\mu (x){)}^2+(\mu (x)-f(x){)}^2]\end{array}$$

对于模型$f(x)$来说，要想让经验风险最小，必须要让上式中与$f(x)$有关的项最小，也就是说当$(\mu (x)-f(x){)}^2$最小即$f(x)=\mu (x)={\mathbb{E}}_{y\sim p_r(y\mid x)}[y]$时，经验风险最小。也就是说，机器学习能学到的最优模型为：
$$f^{\ast }(x)={\mathbb{E}}_{y\sim p_r(y\mid x)}[y]$$
这表明当机器学习取最优模型时，模型的预测值将正好与样本中实际的取值相等。将$f^{\ast }(x)$代回原期望函数：
$$\begin{array}{rl}\mathcal{R}(f)& ={\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(y-f^{\ast }(x)+f^{\ast }(x)-f(x){)}^2]\\ & ={\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(y-f^{\ast }(x){)}^2+(f^{\ast }(x)-f(x){)}^2+2(f^{\ast }(x)-f(x))(y-f^{\ast }(x))]\\ & ={\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(y-f^{\ast }(x){)}^2+(f^{\ast }(x)-f(x){)}^2]\\ & ={\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(y-f^{\ast }(x){)}^2]+{\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(f^{\ast }(x)-f(x){)}^2]\\ & ={\mathbb{E}}_{x\sim p_r(x)}[{\mathbb{E}}_{y\sim p_r(y\mid x)}[(y-f^{\ast }(x){)}^2]]+{\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(f^{\ast }(x)-f(x){)}^2]\\ & ={\mathbb{E}}_{x\sim p_r(x)}[(f(x)-f^{\ast }(x){)}^2]+ϵ\end{array}$$
其中$(y-f^{\ast }(x){)}^2$是模型与最优模型差的平方。$ϵ={\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(y-f^{\ast }(x){)}^2]$表示包含噪声的样本中的$y$与预测出的最优的$y$的损失的期望，也就是期望风险中的噪声，有时候由于样本中的$y$包含噪声从而导致$ϵ$过大，进一步导致期望风险过大，这样的情况是无法通过优化模型来降低的。
在实际训练一个模型时，不同的训练集会得到不同的模型，为了评价机器学习算法（包括模型以及优化算法）的能力，可以用不同训练集上的模型的平均性能评价。令$f_{\mathcal{D}}(x)$表示在训练集$\mathcal{D}$上学习到的模型，只看经验风险函数中跟模型有关的项（也就是暂时不看$ϵ$），对其期望风险进一步做与上面同样方式的配方：
$$\begin{array}{rl}{\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-f^{\ast }(x){)}^2]& ={\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]+{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2]\\ & ={\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]{)}^2+({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2\\ & +2(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)])({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x))]\\ & ={\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]{)}^2+({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2]\\ & +2{\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)])({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x))]\\ & ={\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]{)}^2+({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2]\\ & ={\mathbb{E}}_{\mathcal{D}}[({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2]+{\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]{)}^2]\\ & =({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2+{\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]{)}^2]\end{array}$$
其中，前项$({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2$叫做偏差（bias），记作$(bias.x{)}^2$，表示训练集上模型的期望（模型预测值$y$在数据集上的平均水平）与最优模型期望（数据集上真实值$y$的平均水平）之间的偏差，也就是模型的预测值与训练集上的真实值之间的差距。
后项${\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]{)}^2]$叫做方差（variance），记作$variance.x$，表示训练集上给定$x$模型的预测值与模型的期望之间的偏差，模型的期望表示预测的平均值，与数据集$\mathcal{D}$有关但与给定的$x$无关，是个定值，因此方差实际上表示预测模型不同$x$取值下对应$y$的预测值与数据集上$y$的平均值之间的差异，也就是在该模型下预测值的波动程度。
最后，给出经过偏差-方差分解后完整的期望风险：
$$\begin{array}{rl}\mathcal{R}(f)& =(bias{)}^2+variance+ϵ\\ (bias{)}^2& =({\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]-f^{\ast }(x){)}^2\\ variance& ={\mathbb{E}}_{\mathcal{D}}[(f_{\mathcal{D}}(x)-{\mathbb{E}}_{\mathcal{D}}[f_{\mathcal{D}}(x)]{)}^2]\\ ϵ& ={\mathbb{E}}_{(x,y)\sim p_r(x,y)}[(y-f^{\ast }(x){)}^2]\end{array}$$
在经过上述分解后，在对模型进行选择时，就可以根据偏差和方差来选择最合适的模型。根据不同情况，可以将机器学习模型分为：

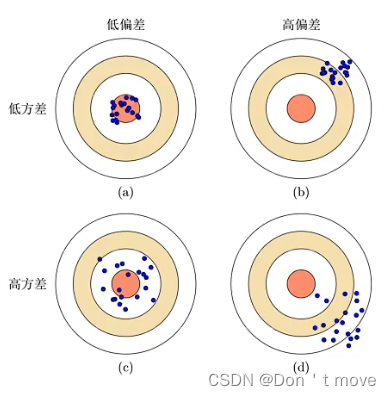
• 低偏差、低方差：模型预测值与真实值相差较小且模型预测值波动幅度不大，是理想的模型
• 高偏差、低方差：模型预测值与真实值相差较大，模型在训练集上预测能力较差，而模型预测值之间的波动幅度较小，模型能力较弱，发生欠拟合现象。
• 低偏差、高方差：模型预测值与真实值相差较小，模型在训练集上预测能力较好，而模型预测值之间的波动幅度较大，模型能力较强，发生过拟合现象。
• 高偏差、高方差：模型预测值与真实值相差较大，模型在训练集上预测能力较差，且模型预测值之间的波动幅度较大，模型能力较强但预测能力差。

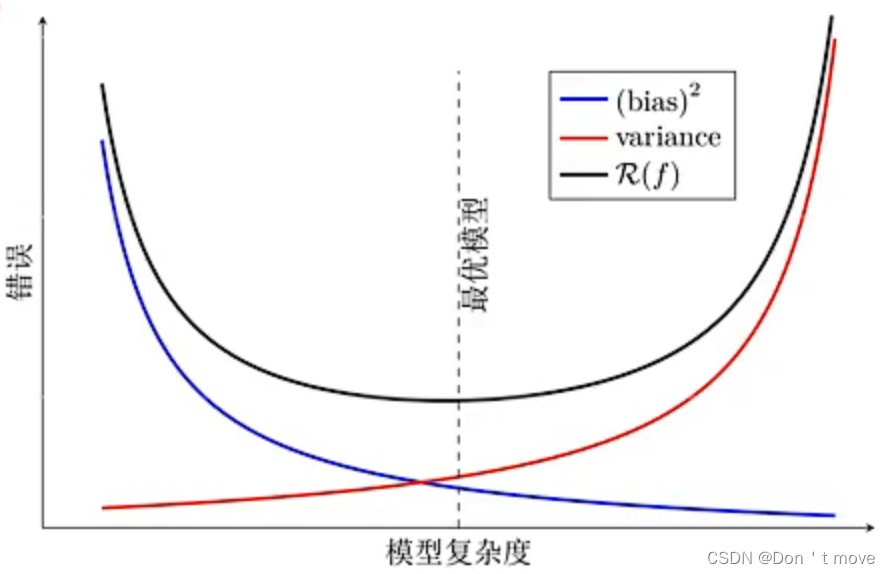
因此，期望风险最小化等价于方差和偏差的最小化。如下图所示，一般来说，随着模型复杂度的增加，模型的偏差会逐渐减小（在训练集上的预测能力增强）、方差会逐渐增大（模型预测的波动增大），若要期望风险最小，就需要取得一个合适的模型，使得二者的和最小。

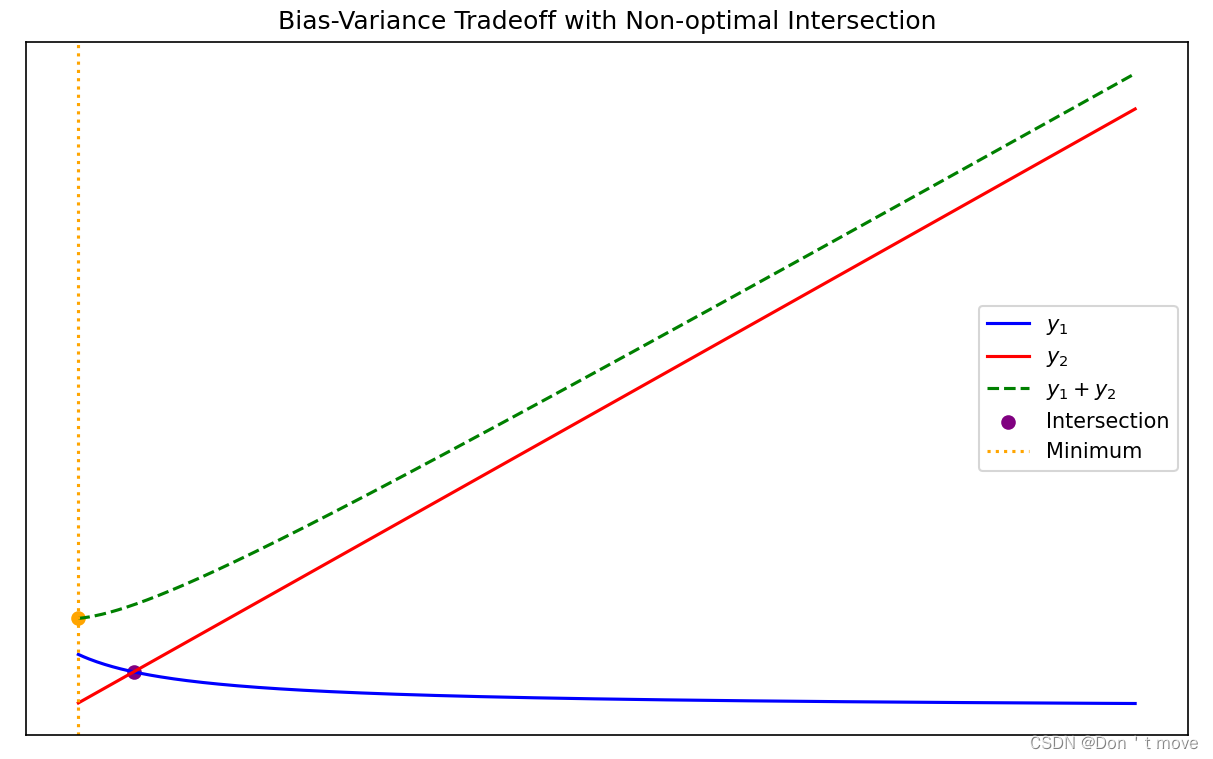
此外还要注意，两曲线的交点不一定是函数最小值点，不知道怎么解释，但是举个反例：
$$\begin{array}{rl}{y}_1& =\frac{1}{x+1}\\ y_2& =x\\ y_1+y_2& =\frac{1}{x+1}+x\end{array}$$
图像如下

---

1. 赤池信息量准则（AIC）和贝叶斯信息准则（BIC）_赤池信息准则-CSDN博客 ↩︎