概率论

概率论

概率的性质

减法公式

·A-B=AB的逆·

应用

画图更简单
abc至少有一个发生表示 P(A并B并C)
P（ABC）《P（AB）=0

条件概率的性质

应用

古典概型

应用:

不放回抽样

全概率公式和贝叶斯公式

全概率公式的使用条件:A事件可以被多个事件分割

一直结果判断情况用贝叶斯公式

应用:

全概率公式


题目10:

事件的独立性

独立性:积的概率等于概率的积

应用

例题12:

解:

离散型随机变量与分布函数

离散型分布函数 是求和，连续型分布函数是求积分

应用：

分布函数

相邻区间变化的概率就是左端点的概率

二项分布和泊松分部

应用：

二项分布


泊松分布：直接套用公式

连续型分布函数

应用：

求概率：

题19：

均匀分布：

应用

正态分布

应用：

画图最简单

离散型随机变量的分布

应用

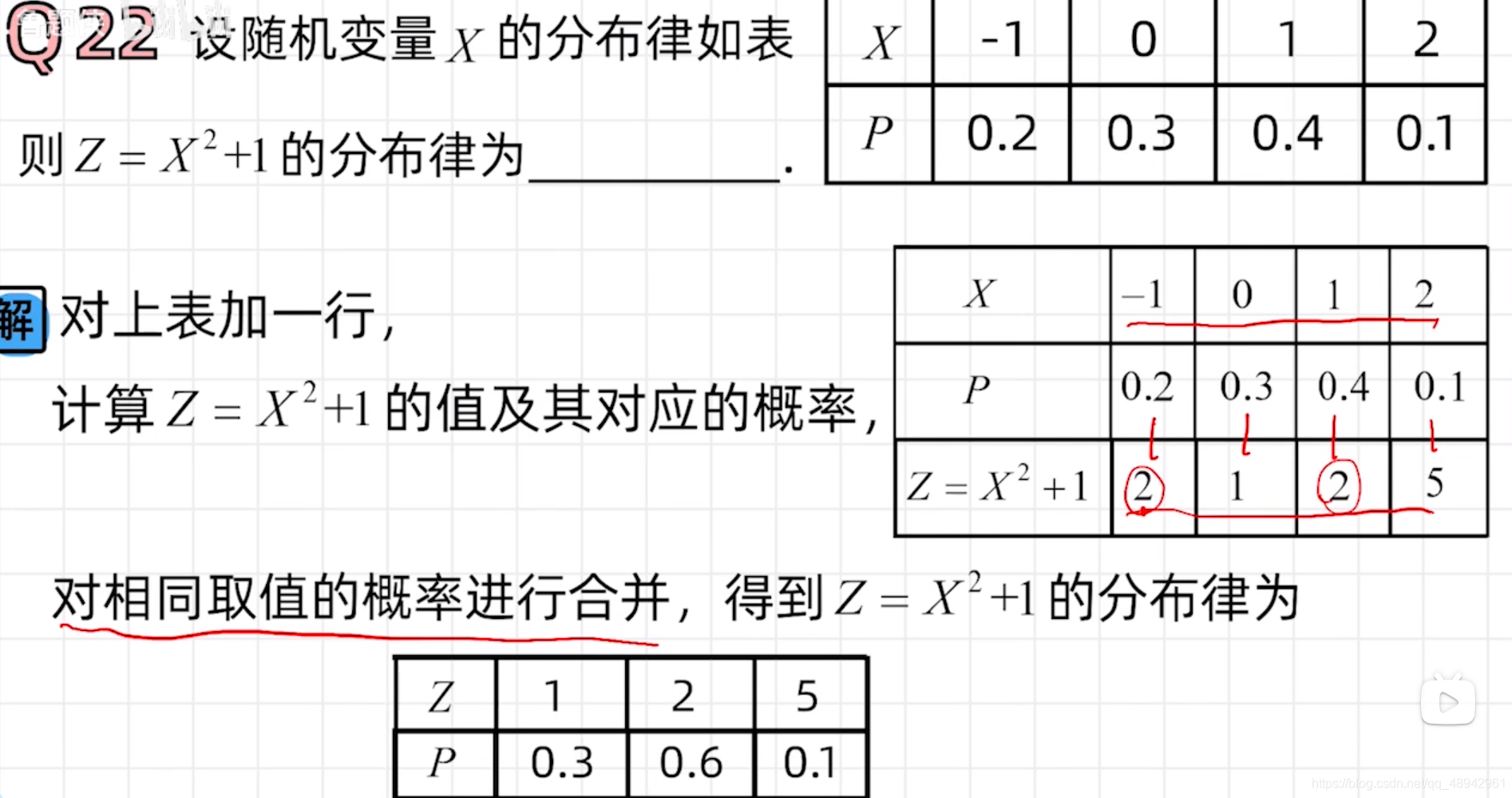
连续型随机变量的函数求导

解法：将Y看做常数，将X由Y表示

应用：

问题23：

问题24 用到了连续型随机变量函数极限为 0 和 1 的性质

二维离散型随机变量的分布

判断X和Y是否独立的条件：p(x=0,y=0)=p(x=0)*p(y=0)

应用：

二维连续型随机变量的分布

应用：

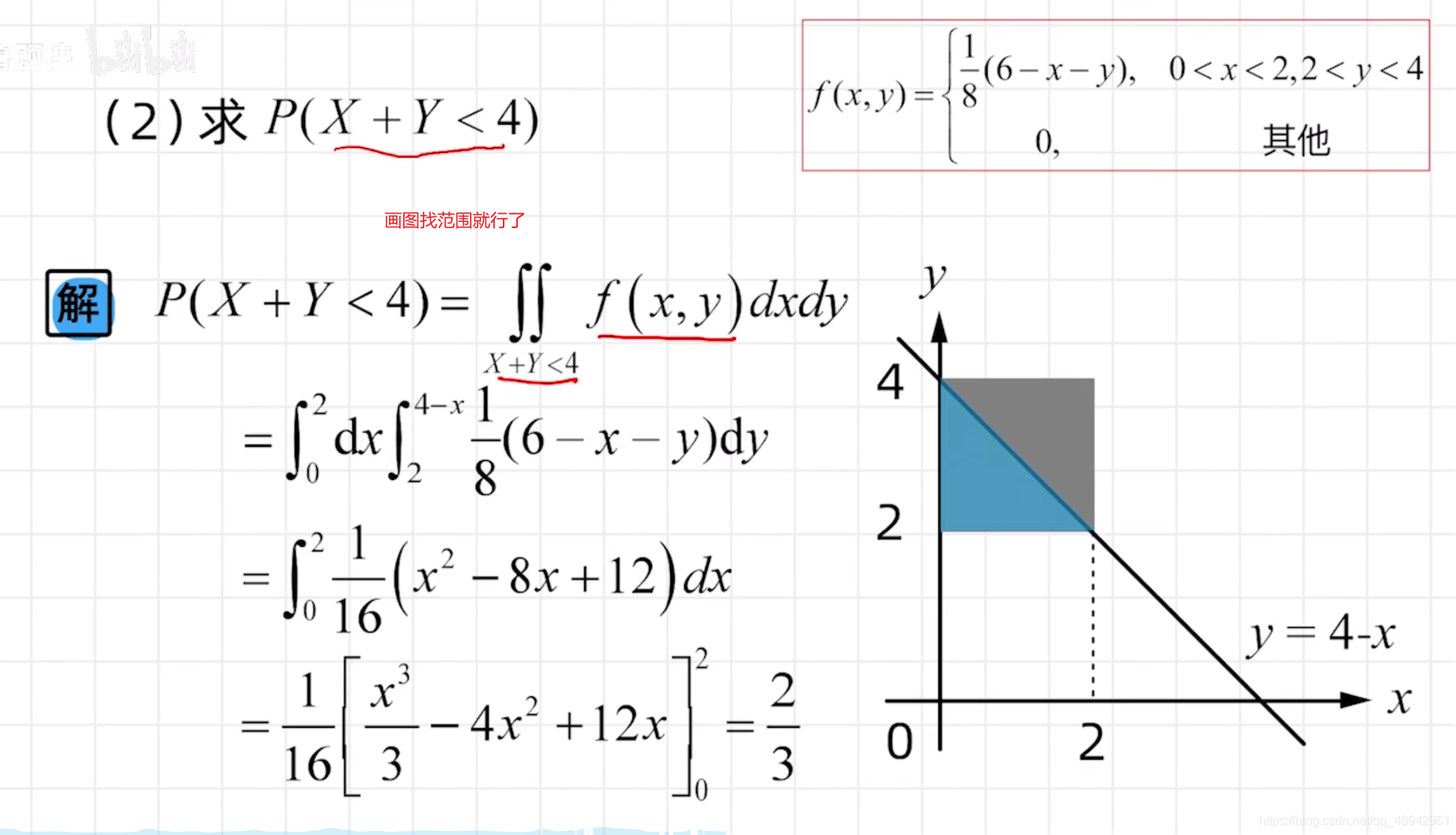
求条件概率

题27：
求边缘密度和联合密度

判断独立性：联合密度等于 边缘密度的积

题目：

二维连续型分布的结合考点

1：求二维连续型分布的密度函数

2.独立性：

应用：

题三十一

正态分布独立性

数学期望

应用：
离散型随机变量的期望

方差和标准差

应用：

二维随机变量的期望和方差

求出边缘分布的期望 就能得到方差

常用分布的期望和方差

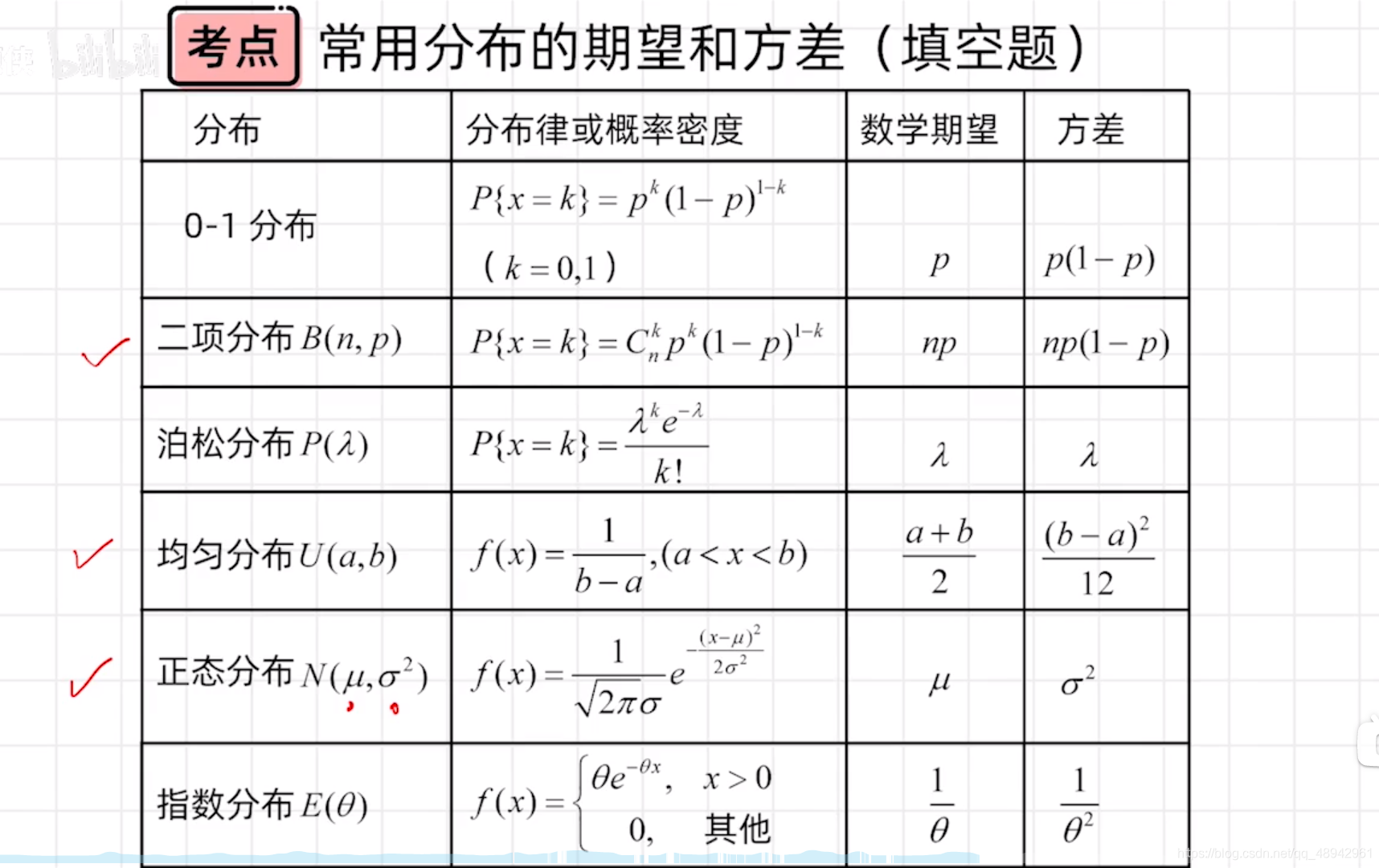
应用：

`平方的期望 = 方差+期望的平方`

题目：37 期望和方差的应用

泊松分布期望的应用：

协方差和相关系数

应用：

连续联合密度函数的方差求法：

1.求出X,Y的边缘密度 求得X或Y的期望 再求积
2.

应用：

随机联合函数的期望和方差

求随机联合函数的相关系数:

三大分布（填空题）

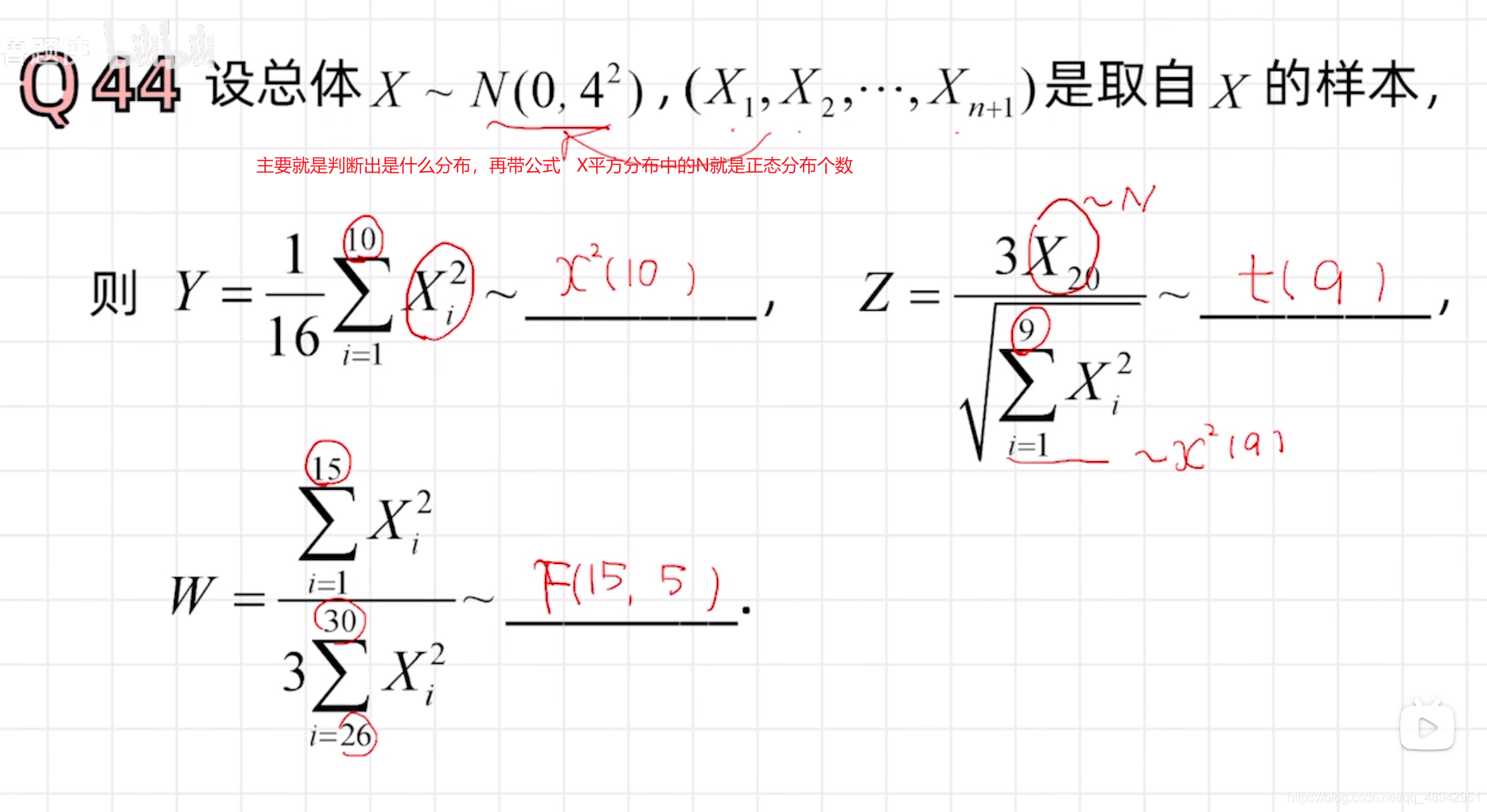
距估计

应用：

离散型随机变量的距估计


连续型随机变量的距估计

中心距与原点矩

第七章:参数估计

样本的距估计总体的原点矩

均匀分布的样本距估计

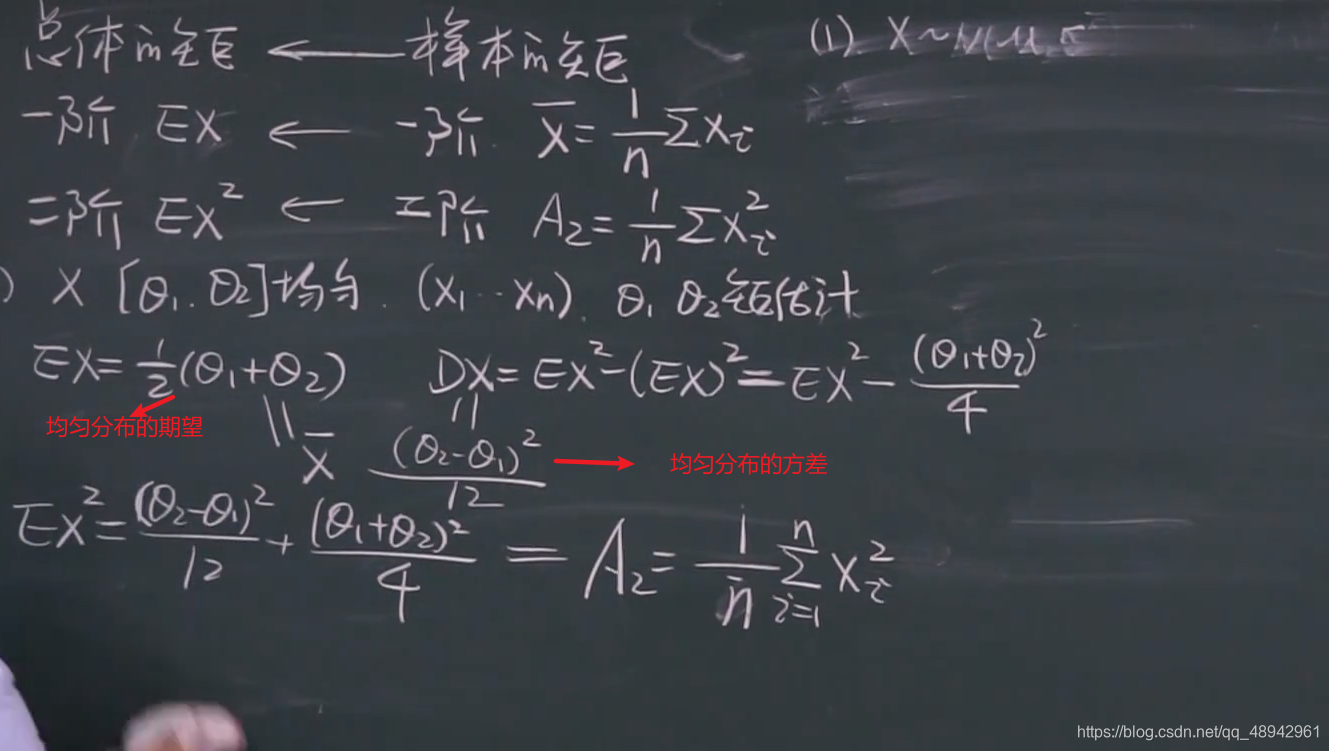
置信区间

枢轴变量的运用

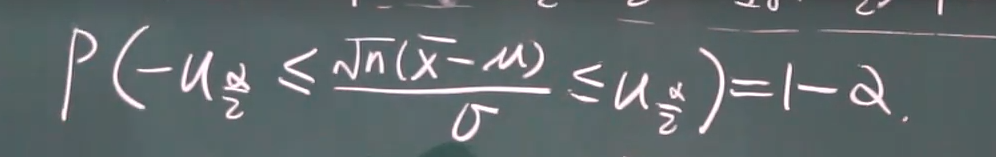
求正太分布的均值或方差估计 色i个嘛已知

总体的塞戈马未知 求正态分布的平均值和方差

样本方差的求法