2024/07/09
校内模拟赛 #1
Codeforces Round 936 (Div. 2) -> E. Girl Permutation
题面:
某个长度为 n n n 的排列需要被猜中。
您将得到其前缀最大值和后缀最大值的索引。
长度为 k k k 的排列是一个大小为 k k k 的数组,从 1 1 1 到 k k k 的每个整数都正好出现一次。
前缀最大值是指在以该元素结尾的前缀上最大的元素。更正式地说,如果每个 j j j < i i i 的 a i a_i ai > a j a_j aj 都是前缀最大值,那么元素 a i a_i ai 就是前缀最大值。
同样,后缀最大值的定义是:如果每个 j j j > i i i 的 a i a_i ai > a j a_j aj 都是后缀最大值,那么元素 a i a_i ai 就是后缀最大值。
您需要输出可能被猜中的不同排列组合的数量。
由于这个数字可能非常大,请输出以 1 0 9 + 7 10^9 + 7 109+7 为模数的答案。
首先,观察题目,不难看出指定位置(前、后缀最大值位置)形成一个 峰,如图:
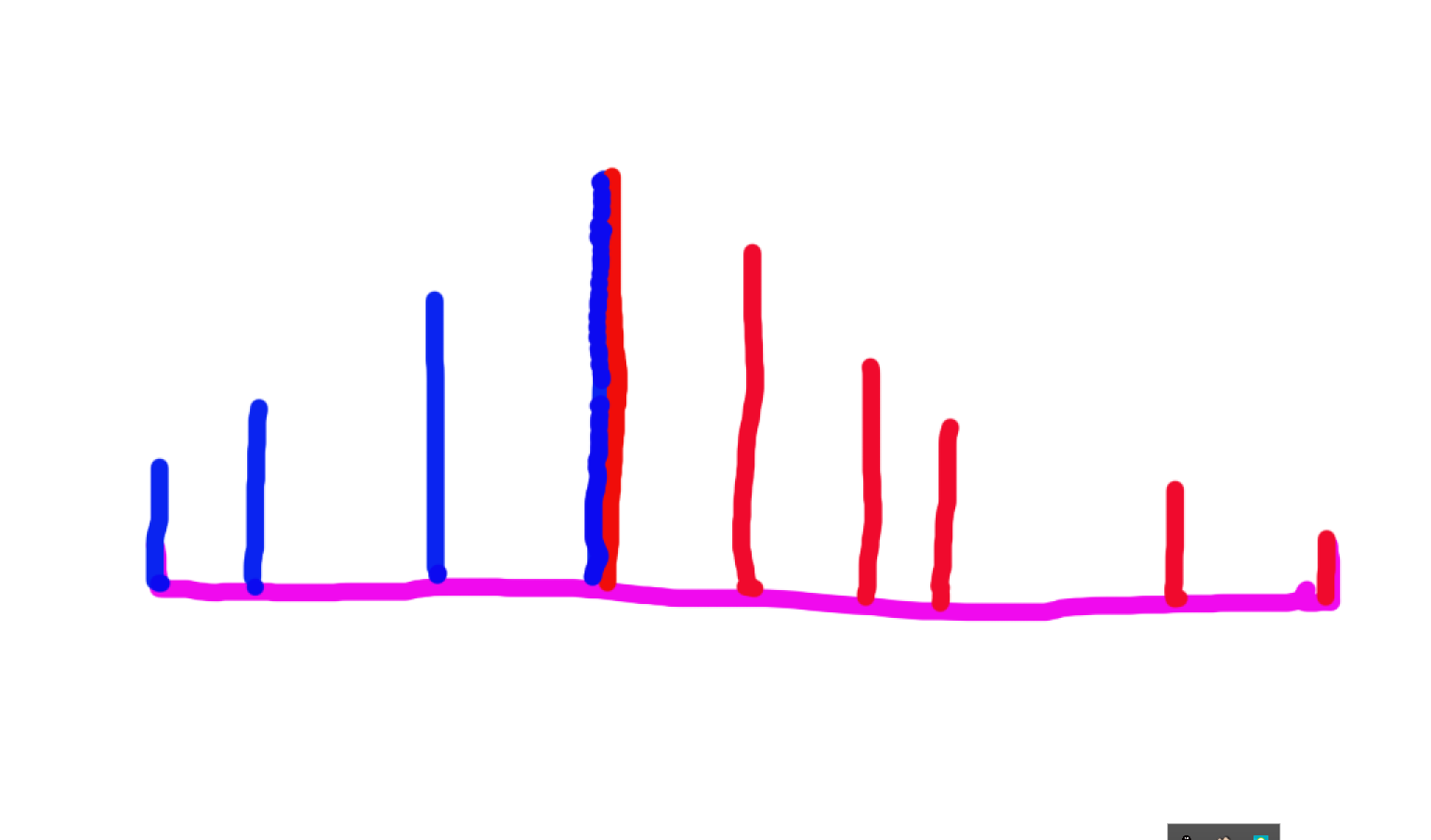
然后,我们不急着去想排列组合
先否定掉最错误的答案———— p 1 p_1 p1 显然是 1 1 1, p m 1 p_{m_1} pm1 显然和 s 1 s_1 s1 相等形成 峰, s m 2 s_{m_2} sm2 显然是 n n n
那么对于不满足上述要求的一律去掉
接下来,我们就可以根据最大值两侧分开分析
我们先看最大值左侧
下文中, a n s ans ans 初值为 1 1 1
当我们确定最大值时,左侧 n − 1 n - 1 n−1 个数可以被选,有 p m 1 − 1 p_{m_1} - 1 pm1−1 个位置,那么 a n s ← a n s ⋅ ( n − 1 p m 1 − 1 ) ans \leftarrow ans \cdot \dbinom{n - 1}{p_{m_1} - 1} ans←ans⋅(pm1−1n−1)
再将 p m 1 − 1 p_{m_1 - 1} pm1−1 位置为界,将左侧又分成 1 ∼ ( p m 1 − 1 − 1 ) 1 \sim (p_{m_1-1} - 1) 1∼(pm1−1−1) 和 ( p m 1 − 1 + 1 ) ∼ ( p m 1 − 1 ) (p_{m_1 - 1} + 1) \sim (p_{m_1} - 1) (pm1−1+1)∼(pm1−1) 两部分
所以 a n s ← a n s ⋅ ( p m 1 − 2 p m 1 − 1 ) ans \leftarrow ans \cdot \dbinom{p_{m_1} - 2}{p_{m_1} - 1} ans←ans⋅(pm1−1pm1−2)
而且 ( p m 1 − 1 + 1 ) ∼ ( p m 1 − 1 ) (p_{m_1 - 1} + 1) \sim (p_{m_1} - 1) (pm1−1+1)∼(pm1−1) 这部分的值可以进行排列
又有 a n s ← a n s ⋅ ( p m 1 − p m 1 − 1 + 1 ) ! ans \leftarrow ans \cdot (p_{m_1} - p_{m_1 - 1} + 1)! ans←ans⋅(pm1−pm1−1+1)!
以此类推,直到分到 p 1 p_1 p1 结束
对于 s s s,自然同理即可
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int mod = 1e9+7;
const int N = 2e5+5;
int fac[N],inv[N];
int qpow(int x,int k) {
int res = 1;
while(k) {
if(k & 1) res = (res * x) % mod;
x = (x * x) % mod;
k >>= 1;
}
return res;
}
int dbinom(int x,int y) {
if(x < y) return 0;
return fac[x] * inv[y] % mod * inv[x - y] % mod;
}
void solve() {
int n = rd(),m1 = rd(),m2 = rd();
vector<int> p(m1 + 1),s(m2 + 1);
for(int i = 1;i<=m1;i++) p[i] = rd();
for(int i = 1;i<=m2;i++) s[i] = rd();
if(p[1] != 1 || p[m1] != s[1] || s[m2] != n) {puts("0");return;}
int res = dbinom(n - 1,p[m1] - 1);
for(int i = m1 - 1;i >= 1;i--) {
res = (res * dbinom(p[i + 1] - 2,p[i] - 1)) % mod;
res = (res * fac[p[i + 1] - p[i] - 1]) % mod;
}
for(int i = 2;i<=m2;i++) {
res = (res * dbinom(n - s[i - 1] - 1,n - s[i])) % mod;
res = (res * fac[(s[i] - s[i-1] - 1)]) % mod;
}
wt(res),putchar('\n');
}
signed main() {
fac[0] = fac[1] = 1;
for(int i = 2;i<=2e5;i++) fac[i] = (fac[i-1] * i) % mod;
inv[0] = inv[1] = 1;
for(int i = 2;i<=2e5;i++) inv[i] = (mod - mod / i) * inv[mod%i] % mod;
for(int i = 2;i<=2e5;i++) inv[i] = inv[i-1] * inv[i] % mod;
int t = rd();
while(t--) solve();
return 0;
}
P3924 康娜的线段树
题面:
题目描述
小林是个程序媛,不可避免地康娜对这种人类的“魔法”产生了浓厚的兴趣,于是小林开始教她OI。
今天康娜学习了一种叫做线段树的神奇魔法,这种魔法可以维护一段区间的信息,是非常厉害的东西。康娜试着写了一棵维护区间和的线段树。由于她不会打标记,因此所有的区间加操作她都是暴力修改的。具体的代码如下:
struct Segment_Tree{ #define lson (o<<1) #define rson (o<<1|1) int sumv[N<<2],minv[N<<2]; inline void pushup(int o){sumv[o]=sumv[lson]+sumv[rson];} inline void build(int o,int l,int r){ if(l==r){sumv[o]=a[l];return;} int mid=(l+r)>>1; build(lson,l,mid);build(rson,mid+1,r); pushup(o); } inline void change(int o,int l,int r,int q,int v){ if(l==r){sumv[o]+=v;return;} int mid=(l+r)>>1; if(q<=mid)change(lson,l,mid,q,v); else change(rson,mid+1,r,q,v); pushup(o); } }T;在修改时,她会这么写:
for(int i=l;i<=r;i++)T.change(1,1,n,i,addv);显然,这棵线段树每个节点有一个值,为该节点管辖区间的区间和。
康娜是个爱思考的孩子,于是她突然想到了一个问题:
如果每次在线段树区间加操作做完后,从根节点开始等概率的选择一个子节点进入,直到进入叶子结点为止,将一路经过的节点权值累加,最后能得到的期望值是多少?
康娜每次会给你一个值 q w q qwq qwq ,保证你求出的概率乘上 q w q qwq qwq 是一个整数。
这个问题太简单了,以至于聪明的康娜一下子就秒了。
现在她想问问你,您会不会做这个题呢?
输入格式
第一行整数 n , m , q w q n,m,qwq n,m,qwq 表示线段树维护的原序列的长度,询问次数,分母。
第二行 n n n 个数,表示原序列。
接下来 m m m 行,每行三个数 l , r , x l,r,x l,r,x 表示对区间 [ l , r ] [l,r] [l,r] 加上 x x x
输出格式
共 m m m 行,表示期望的权值和乘上qwq结果。
样例 #1
样例输入 #1
8 2 1 1 2 3 4 5 6 7 8 1 3 4 1 8 2样例输出 #1
90 120提示
对于30%的数据,保证 1 ≤ n , m ≤ 100 1 \leq n,m \leq 100 1≤n,m≤100
对于70%的数据,保证 1 ≤ n , m , ≤ 1 0 5 1 \leq n,m, \leq 10^{5} 1≤n,m,≤105
对于100%的数据,保证$1 \leq n,m \leq 10^6 $
− 1000 ≤ a i , x ≤ 1000 -1000 \leq a_i,x \leq 1000 −1000≤ai,x≤1000
这个线段树成功让我在赛时卡了足足 5 h 5h 5h 还只拿了 50 50 50 分
但是,这道题让我找到了造新题的思路
先上场的是我的难绷思路:(大家可以直接跳转到 正解)
我们可以注意到
根据 期望定义,$ 期望 = (基本事件值总和) / 基本事件数 $
基本事件数不变,那么每次询问只改变 基本事件总和
所以初始数组,每一次询问,都是可以分开分析的
面对这样一个线段树,如图:
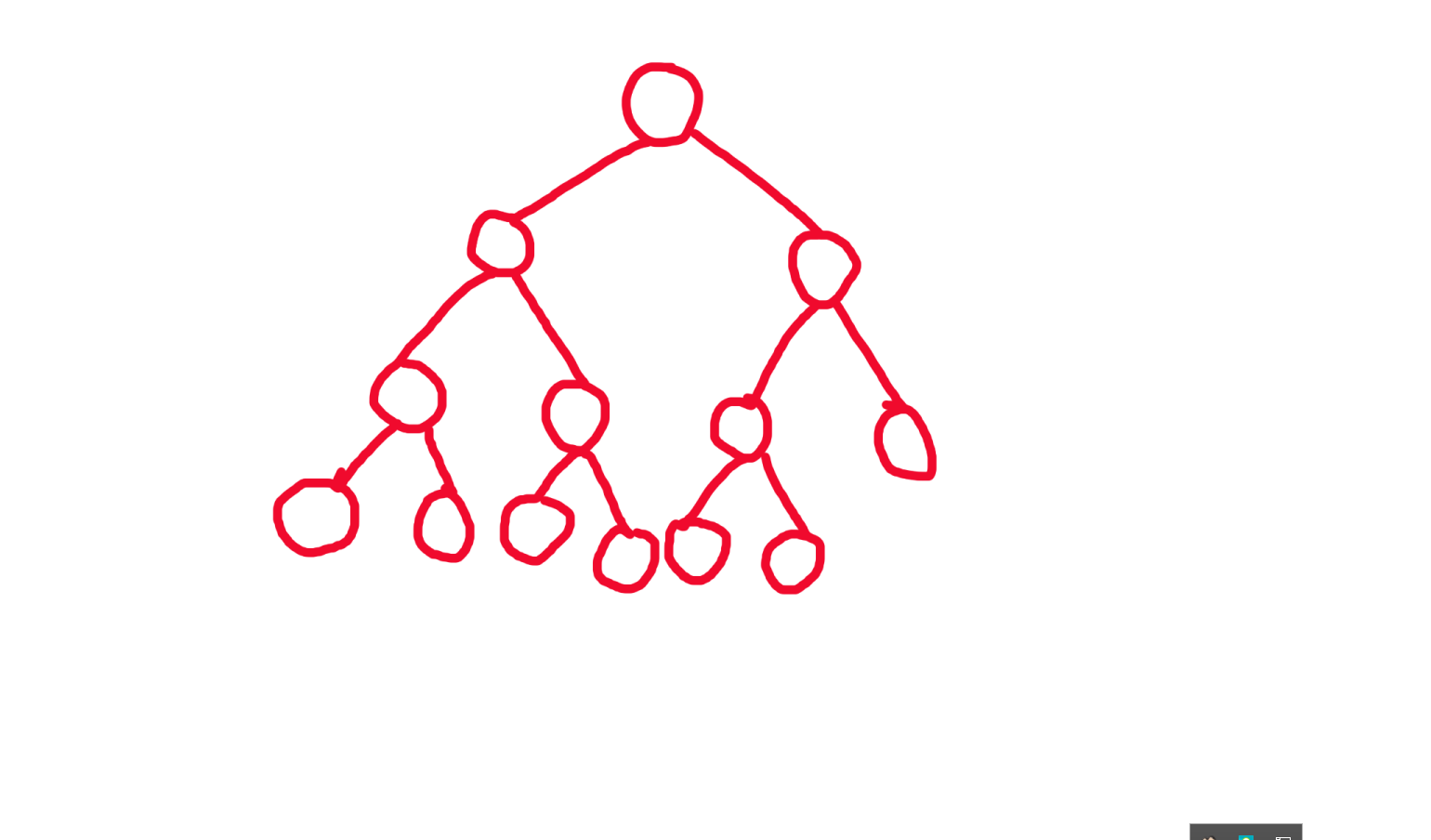
因为线段树只有最后一层不满,因此,我们可以发现
P
(
每个以最后一层叶子节点为终点的路径的概率
)
=
1
2
P
(
每个以倒数第
2
层的叶子节点为终点的路径概率
)
P(每个以最后一层叶子节点为终点的路径的概率) = \frac{1}{2}P(每个以倒数第 2 层的叶子节点为终点的路径概率)
P(每个以最后一层叶子节点为终点的路径的概率)=21P(每个以倒数第2层的叶子节点为终点的路径概率)
我们就让 前者 = 1 前者 = 1 前者=1, 后者 = 2 后者 = 2 后者=2,建一颗辅助线段树去查询每个节点被访问的次数
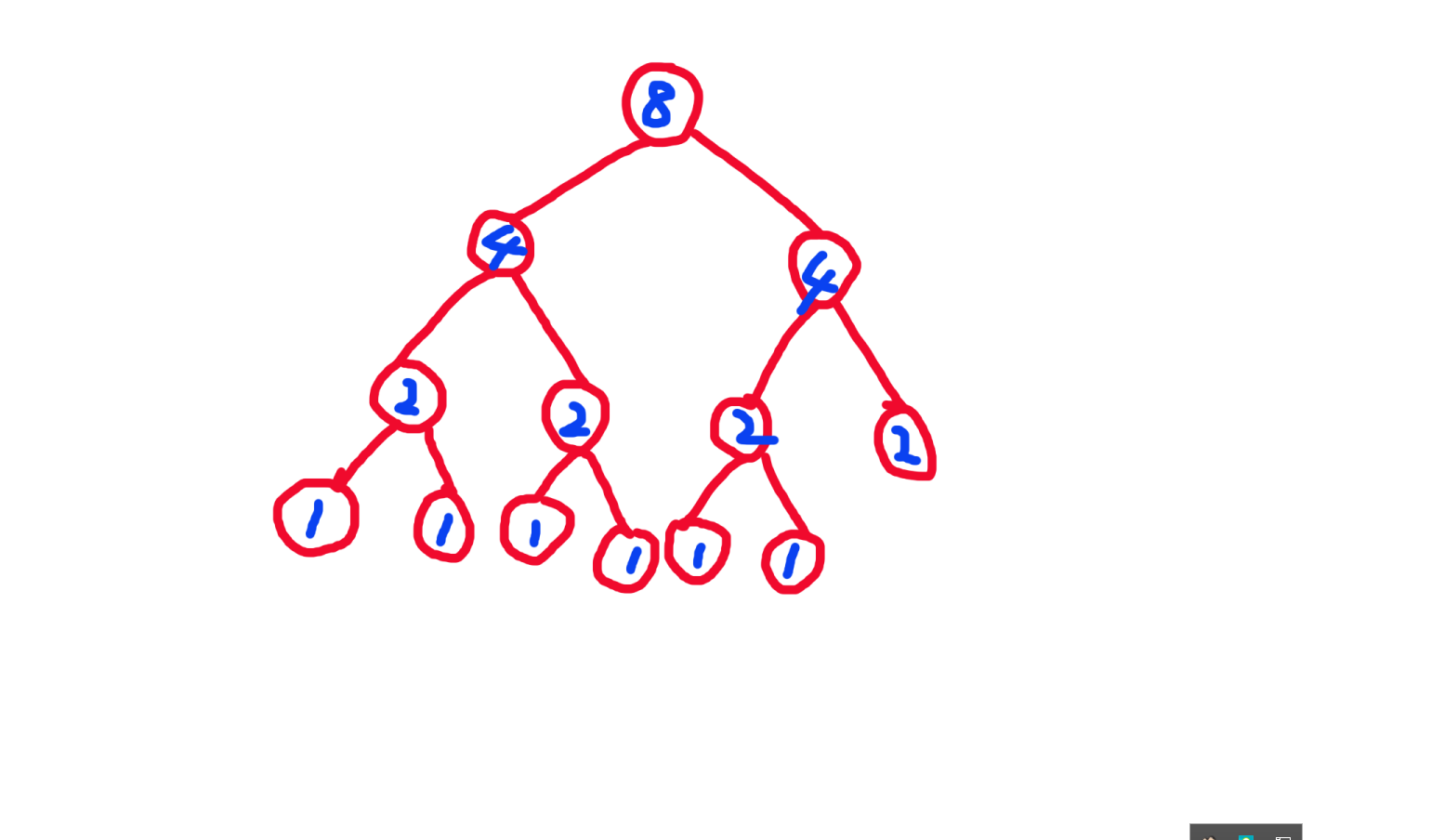
然后再 b u i l d build build 一颗正常线段树,让 a 数组的贡献 → a n s a 数组的贡献 \rightarrow ans a数组的贡献→ans
初始数组搞定,然后是每一次询问
当我们模拟过程时,将每一次累加值都拆开
就会发现:
令
v
=
询问值
,
l
e
n
=
询问覆盖的区间长度
,
t
=
访问总次数
v = 询问值\ \ ,\ \ len = 询问覆盖的区间长度\ \ ,\ \ t = 访问总次数
v=询问值 , len=询问覆盖的区间长度 , t=访问总次数
那么,对于任意一个节点,贡献为 v ⋅ l e n ⋅ t v \cdot len \cdot t v⋅len⋅t
又因为对于每一次询问, v v v 始终是定值,
那么,对于一段询问区间,有:
贡献总和 = ∑ i ∈ 涵盖 l , r 的节点 v l e n i t i = v ∑ i ∈ 被 l , r 覆盖的节点 l e n i t i 贡献总和 = \sum_{i \in 涵盖l,r的节点} vlen_it_i =\ v\sum_{i \in 被l,r覆盖的节点}len_it_i 贡献总和=i∈涵盖l,r的节点∑vleniti= vi∈被l,r覆盖的节点∑leniti
那么,用一颗树剖树去维护这个 ‘ ∑ \sum ∑’,难绷的思路就结束了
DEAD-code:
#include<bits/stdc++.h>
using namespace std;
#define int __int128
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 1e6+5;
bool Mbe;
int n,m,q,a[N];
int nxt[N<<1],to[N<<1],cnt,head[N];
void init() {
memset(head,-1,sizeof(head));
}
void add(int u,int v) {
nxt[cnt] = head[u];
to[cnt] = v;
head[u] = cnt++;
}
int qt[N<<2];
namespace Segtree_2{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
void push_up(int p) {
qt[p] = qt[ls] + qt[rs];
}
void build(int p,int pl,int pr) {
if(pl == pr) {qt[p]++;return;}
build(ls,pl,mid);
if(mid + 1 == pr && pl != mid) qt[rs]++;
build(rs,mid+1,pr);
push_up(p);
}
void build_QTree(int p,int pl,int pr) {
int f = (p >> 1);
qt[p] *= (pr - pl + 1);
add(f,p);
add(p,f);
if(pl == pr) return;
build_QTree(ls,pl,mid);
build_QTree(rs,mid+1,pr);
}
#undef ls
#undef rs
#undef mid
}
int fa[N<<2],top[N<<2],dep[N<<2],son[N<<2],siz[N<<2],id[N<<2];
void dfs1(int x,int f){
fa[x] = f;
siz[x] = 1;
dep[x] = dep[f] + 1;
for(int i = head[x];~i;i = nxt[i]) {
int y = to[i];
if(y ^ f) {
dfs1(y,x);
siz[x] += siz[y];
if(siz[son[x]] < siz[y]) son[x] = y;
}
}
}
int num,w_new[N<<2];
void dfs2(int x,int topx){
top[x] = topx;
id[x] = ++num;
w_new[num] = qt[x];
if(!son[x]) return;
dfs2(son[x],topx);
for(int i = head[x];~i;i = nxt[i]) {
int y = to[i];
if(y ^ fa[x] && y ^ son[x]) dfs2(y,y);
}
}
namespace QTree{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
int t[N<<4];
void push_up(int p) {
t[p] = t[ls] + t[rs];
}
void build(int p,int pl,int pr) {
if(pl == pr) {
t[p] = w_new[pl];
return;
}
build(ls,pl,mid);
build(rs,mid+1,pr);
push_up(p);
}
int query(int p,int pl,int pr,int l,int r) {
if(l <= pl && pr <= r) return t[p];
int res = 0;
if(l <= mid) res += query(ls,pl,mid,l,r);
if(r > mid) res += query(rs,mid+1,pr,l,r);
return res;
}
#undef ls
#undef rs
#undef mid
}
int query_tree(int x) {
return QTree::query(1,1,num,id[x],id[x] + siz[x] - 1);
}
int ans = 0;
namespace Segtree_1{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
int t[N<<2];
void push_up_build(int p,int pl,int pr) {
t[p] = t[ls] + t[rs];
ans += t[p] * qt[p]/ (pr - pl + 1);
}
void build(int p,int pl,int pr) {
if(pl == pr) {
t[p] = a[pl];
ans += t[p] * qt[p];
return;
}
build(ls,pl,mid);
build(rs,mid+1,pr);
push_up_build(p,pl,pr);
}
#undef ls
#undef rs
#undef mid
}
#define ls (p << 1)
#define rs (ls | 1)
int query_range(int p,int pl,int pr,int l,int r,int v) {
if(l <= pl && pr <= r) return query_tree(p) * v;
int res = qt[p] / (pr - pl + 1) * v * (min(r,pr) - max(l,pl) + 1),mid = (pl + pr) >> 1;
if(l <= mid) res += query_range(ls,pl,mid,l,r,v);
if(r > mid) res += query_range(rs,mid+1,pr,l,r,v);
return res;
}
#undef ls
#undef rs
bool Med;
signed main() {
// freopen("P3924_1.in","r",stdin);
// freopen("ans.out","w",stdout);
fprintf(stderr, "%.3lf MB\n", (&Med - &Mbe) / 1048576.0);
init();
n = rd(),m = rd(),q = rd();
for(int i = 1;i<=n;i++) a[i] = rd();
Segtree_2::build(1,1,n);
Segtree_2::build_QTree(1,1,n);
Segtree_1::build(1,1,n);
dfs1(1,0);dfs2(1,1);
QTree::build(1,1,num);
while(m--) {
int l = rd(),r = rd(),x = rd();
ans += query_range(1,1,n,l,r,x);
wt(ans * q * n/ qt[1]);
putchar('\n');
}
return 0;
}
记录:

正解
今天太累了,待补
在此感谢ckain大佬的讲解
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6+5;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
int a[N],n,m,qwq,s[N];
int t[N<<2],dep[N<<2],maxd;
#define ls (p << 1)
#define rs (p << 1 | 1)
#define mid ((pl + pr ) >> 1)
void build(int p,int pl,int pr,int d) {
if(pl == pr) {
dep[pl] = d;
maxd = max(d,maxd);
t[p] = a[pl];
return;
}
build(ls,pl,mid,d + 1);
build(rs,mid+1,pr,d + 1);
t[p] = t[ls] + t[rs];
}
int query(int p,int pl,int pr,int T,int tt) {
if(pl == pr) return (1 << T) * (tt + t[p]);
return query(ls,pl,mid,T - 1,tt + t[p]) + query(rs,mid+1,pr,T - 1,tt + t[p]);
}
#undef ls
#undef rs
#undef mid
signed main() {
n = rd(),m = rd(),qwq = rd();
for(int i = 1;i<=n;i++) a[i] = rd();
build(1,1,n,1);
int ans = query(1,1,n,maxd - 1,0);
int y = (1<<(maxd - 1));
int gcd = __gcd(y,qwq);
y /= gcd;
qwq /= gcd;
for(int i = 1;i<=n;i++) s[i] = s[i-1] + (((1 <<(dep[i])) - 1) << (maxd - dep[i]));
while(m--) {
int l = rd(),r = rd(),x = rd();
ans += (s[r] - s[l - 1]) * x;
wt(ans / y * qwq),putchar('\n');
}
return 0;
}
P8352 [SDOI/SXOI2022] 小 N 的独立集
题面:
[SDOI/SXOI2022] 小 N 的独立集
题目描述
小 N 喜欢出最大权独立集问题。
有一天,他接到了一系列的出题任务,于是他顺手出了一系列最大权独立集问题。
为了同时给这一系列题目造数据,小 N 生成了一个 n n n 个点的树,并选定了一个正整数 k k k。这样每生成一组数据时,他只需要对于每个点,随机生成一个在 1 ∼ k 1 \sim k 1∼k 之间的整数点权,就可>以生成一个新的最大独立集问题。
小 N 把这些题给了他的好朋友,小 Ω。小 Ω 表示,这些题太多太乱了,他打算把所有的 k n k^n kn 道题归类处理。一个自然的想法就是按答案(也就是最大权独立集中的点的权值之和)分类,显然这>些最大权独立集问题的答案一定在 1 ∼ n k 1 \sim nk 1∼nk 之间,所以小 Ω 只需要将所有题目按照答案分成 n k nk nk 类进行管理就行了。
在小 N 正式开始出题之前,小 Ω 先要算出每一类题目具体有多少道。稍加估计之后小 Ω 很快意识到自己并没有《诗云》中描述的那种存储器,于是断然拒绝了小 N 关于“先把所有可能的题目造好>再慢慢分类统计数量”的建议,然后悲剧地意识到自己并不会计算这些数字。
他想叫你帮他解决这个问题,还说如果你成功解决了这个问题,那么在小 N 出那些最大权独立集问题的时候,他会帮你提交一份标程代码。
输入格式
第一行, 2 2 2 个正整数 n n n, k k k。
接下来 n − 1 n-1 n−1 行,每行 2 2 2 个正整数 u i u_i ui, v i v_i vi,描述一条连接点 u i u_i ui 和 v i v_i vi 的边,保证这些边构成一棵树。
输出格式
n k nk nk 行,每行一个整数,第 i i i 个整数表示在所有可能的题目中,最大权独立集大小为 i i i 的有多少道,答案对 1 0 9 + 7 10^9+7 109+7 取模。
样例 #1
样例输入 #1
4 2 1 2 2 3 2 4样例输出 #1
0 0 2 6 6 2 0 0提示
【样例解释】
符合题意的最大权独立集题目一共有 2 4 = 16 2^4=16 24=16 道。
可以证明,当点 1 1 1, 3 3 3, 4 4 4 的权值均为 1 1 1 时,最大权独立集为 3 3 3 ,这样的题目共有 2 2 2 道;点 1 1 1, 3 3 3, 4 4 4 的权值恰有一个为 2 2 2 时,最大权独立集为 4 4 4 ,这样的题目共>有 6 6 6 道;对于最大权独立集为 5 5 5 或 6 6 6 的情况也是类似的。
【数据范围】
对于 15 % 15 \% 15% 的数据, n ≤ 8 n \leq 8 n≤8;
对于 30 % 30 \% 30% 的数据, n ≤ 30 n \leq 30 n≤30;
对于 50 % 50 \% 50% 的数据, n ≤ 100 n \leq 100 n≤100;
对于另外 10 % 10 \% 10% 的数据, k = 1 k=1 k=1;
对于另外 15 % 15 \% 15% 的数据, k = 2 k=2 k=2;
对于 100 % 100 \% 100% 的数据, n ≤ 1000 n \leq 1000 n≤1000, k ≤ 5 k \leq 5 k≤5, u i , v i ≤ n u_{i}, v_{i} \leq n ui,vi≤n。【提示】
最大权独立集问题是指:选择一个点集,使得任意两个被选择的点都没有边直接相连,并且使得所有被选择的点的点权之和最大。
此题思路非常有趣,我觉得这个思路可以叫做 放缩状态优化
首先,我们正常去思考出一个多项式复杂度算法
这不难看出是一道 d p dp dp 套 d p dp dp 题
那么我们二话不说,先设内层 d p dp dp: g i , 0 g_{i,0} gi,0 是 i i i 节点不取的最大权独立集, g i , 1 g_{i,1} gi,1 是 i i i 节点取的最大权独立集
所以,自然而然的,我们再设出 f x , i , j f_{x,i,j} fx,i,j 表示在 x x x 节点符合要求的方案数,其中 i = g i , 0 i = g_{i,0} i=gi,0, j = g i , 1 j = g_{i,1} j=gi,1
那么,根据最大权独立集的dp转移,该转移自然就出来了:
令 v v v 节点方案数为 f y , p , q f_{y,p,q} fy,p,q, u u u 节点方案数为 f x , i , j f_{x,i,j} fx,i,j
对于
v
v
v 作为
u
u
u 的孩子,让
v
v
v 合并至
u
u
u 中,则
f
x
,
i
+
m
a
x
(
p
,
q
)
,
j
+
p
′
+
f
x
,
i
,
j
×
f
y
,
p
,
q
→
f
x
,
i
+
m
a
x
(
p
,
q
)
,
j
+
p
′
其中,
f
′
为
N
e
w
F
,
f
为
O
l
d
F
f^{\prime}_{x,i + max(p,q),j + p} + f_{x,i,j} \times f_{y,p,q} \rightarrow f^{\prime}_{x,i + max(p,q),j + p} \\ 其中,f^{\prime} 为 New\ F,f 为 Old\ F
fx,i+max(p,q),j+p′+fx,i,j×fy,p,q→fx,i+max(p,q),j+p′其中,f′为New F,f为Old F
树上背包复杂度分析,鉴定为 O ( n 4 k 4 ) O(n^4k^4) O(n4k4),无法接受
我们发现题目中还有一个信息没有用上
k ≤ 5 k \leq 5 k≤5
这个 k k k 非常小,那么我们就要用这个支点,优化状态结构
怎么造出 k k k 的有利条件呢? 答案是放缩
我们设计的 g g g 函数条件太苛刻,状态太绝对了
如果读者有写过 P4719 【模板】“动态 DP”&动态树分治,就会想到 g i , 1 g_{i,1} gi,1 可以表示为 强制不选择本节点取得的最大权独立集,而 g i , 0 g_{i,0} gi,0 为不强制选择本节点取得的最大权独立集
这样,放缩就比较明显了,对于 g i , 0 g_{i,0} gi,0 和 g i , 1 g_{i,1} gi,1,中间缺什么呢?
我们知道,不强制选择肯定最优,强制不选择不一定优,
那么,容易得到强制不选择的答案一定无限趋近与不强制选择的答案,而其中 差值 ≤ v a l i 差值 \leq val_i 差值≤vali (因为强制不选择对于强制选择来说更灵活,所以与不强制选择相差不会超过 v a l i val_i vali)
即:
0
≤
g
i
,
0
−
g
i
,
1
≤
v
a
l
i
0 \leq g_{i,0} - g_{i,1} \leq val_i
0≤gi,0−gi,1≤vali
又因为, 每个节点的权值 ≤ k 每个节点的权值 \leq k 每个节点的权值≤k
所以
0
≤
g
i
,
0
−
g
i
,
1
≤
v
a
l
i
≤
k
0 \leq g_{i,0} - g_{i,1} \leq val_i \leq k
0≤gi,0−gi,1≤vali≤k
放缩结束!
那么,我们不用再枚举庞大的 d p dp dp 内存,只需要寻找 f i , 1 + i ( i = 0 ∼ k ) f_{i,1} + i (i = 0 \sim k) fi,1+i(i=0∼k) 的位置就可以了
此时自然得出 f u , v 1 , d f_{u,v_1,d} fu,v1,d 表示 u u u 子树中 g u , 0 , g u , 1 g_{u,0},g_{u,1} gu,0,gu,1 分别为 v 1 + d , v 1 v_1+d,v1 v1+d,v1 时的方案数,依然枚举 i , j , p , q i,j,p,q i,j,p,q,有转移:
f u , i + p + q , max ( i + j + p , i + p + q ) − ( i + p + q ) ← f u , i + p + q , max ( i + j + p , i + p + q ) − ( i + p + q ) + f u , i , j × f v , p , q f_{u,i+p+q,\max(i+j+p,i+p+q)-(i+p+q)} \gets f_{u,i+p+q,\max(i+j+p,i+p+q)-(i+p+q)}+ f_{u,i,j} \times f_{v,p,q} fu,i+p+q,max(i+j+p,i+p+q)−(i+p+q)←fu,i+p+q,max(i+j+p,i+p+q)−(i+p+q)+fu,i,j×fv,p,q
tips: 为了对比,这里展示出原先的式子中变化:
i → ( i + j ) j → j p → ( p + q ) q → q 原式 = f x , i + m a x ( p , q ) , j + p ′ + f x , i , j × f y , p , q → f x , i + m a x ( p , q ) , j + p ′ 其中 f 的第 3 项含义变成了 f i , x , y − f j , p , q 的大小 i \rightarrow (i + j) \\ j \rightarrow j \\ p \rightarrow (p + q)\\ q \rightarrow q\\ 原式 = f^{\prime}_{x,i + max(p,q),j + p} + f_{x,i,j} \times f_{y,p,q} \rightarrow f^{\prime}_{x,i + max(p,q),j + p} \\ 其中 f 的 第3项含义变成了 f_{i,x,y} - f_{j,p,q} 的大小 i→(i+j)j→jp→(p+q)q→q原式=fx,i+max(p,q),j+p′+fx,i,j×fy,p,q→fx,i+max(p,q),j+p′其中f的第3项含义变成了fi,x,y−fj,p,q的大小
此题结束!
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 1005,mod = 1e9+7;
int n,k;
int head[N],nxt[N<<1],to[N<<1],cnt;
void init() {memset(head,-1,sizeof(head));}
void add(int u,int v) {
nxt[cnt] = head[u];
to[cnt] = v;
head[u] = cnt++;
}
int siz[N],f[N][N * 5][6],g[N * 5][6];
inline void Add(int &a,int b){a += b;if(a >= mod) a -= mod;}
void dp(int x,int fa) {
siz[x] = 1;
for(int i = 1;i<=k;i++) f[x][0][i] = 1;
for(int T = head[x];~T;T = nxt[T]) {
int y = to[T];
if(y == fa) continue;
dp(y,x);
memset(g,0,sizeof(g));
for(int i = 0;i <= k * siz[x];i++)
for(int j = 0;j<=k;j++)
if(f[x][i][j])
for(int p = 0;p <= k * siz[y];p++)
for(int q = 0;q <= k;q++)
if(f[y][p][q])
Add(g[i + p + q][max(i + j + p,i + p + q) - (i + p + q)],f[x][i][j] * f[y][p][q] % mod);
memcpy(f[x],g,sizeof(g));
siz[x] += siz[y];
}
}
signed main() {
init();
n = rd(),k = rd();
for(int i = 1,u,v;i<n;i++) {
u = rd(),v = rd();
add(u,v);
add(v,u);
}
dp(1,0);
for(int i = 1;i<=k * n;i++) {
int ans = 0;
for(int d = 0;d<=min(i,k);d++) Add(ans,f[1][i - d][d]);
wt(ans),putchar('\n');
}
return 0;
}
回顾老题,典中典之新手恶梦
P2572 [SCOI2010] 序列操作
没什么好说的,慢慢实现就好了
关键是各功能之间的影响、关系要理清!
AC-code:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n,m,a[N];
namespace sgm{
#define ls (p << 1)
#define rs (p << 1 | 1)
#define mid ((pl + pr) >> 1)
struct node{
int l,r,lmax,rmax,mx,sum;
node(int kl,int kr,int lm,int rm,int kmx,int s){
l = kl,r = kr;
lmax = lm,rmax = rm,mx = kmx,sum = s;
}
node() {}
};
int L[N<<2],R[N<<2],mx[N<<2][2],cov[N<<2],lmax[N<<2][2],rmax[N<<2][2],sum[N<<2][2],rev[N<<2];
void newnode(int p,int pos) {
L[p] = R[p] = a[pos];
lmax[p][a[pos]] = rmax[p][a[pos]] = 1;
mx[p][a[pos]] = sum[p][a[pos]] = 1;
}
void push_up(int p,int pl,int pr) {
L[p] = L[ls],R[p] = R[rs];
for(int i = 0;i<2;i++) {
lmax[p][i] = lmax[ls][i];
rmax[p][i] = rmax[rs][i];
sum[p][i] = sum[ls][i] + sum[rs][i];
mx[p][i] = max(mx[ls][i],mx[rs][i]);
if(R[ls] == L[rs] && L[rs] == i) {
if(sum[ls][i] == mid - pl + 1) lmax[p][i] += lmax[rs][i];
if(sum[rs][i] == pr - mid) rmax[p][i] += rmax[ls][i];
mx[p][i] = max(mx[p][i],lmax[rs][i] + rmax[ls][i]);
}
}
}
void build(int p,int pl,int pr) {
cov[p] = -1,rev[p] = 0;
if(pl == pr) {newnode(p,pl);return;}
build(ls,pl,mid);
build(rs,mid+1,pr);
push_up(p,pl,pr);
}
void addCov(int p,int pl,int pr,int d){
cov[p] = d;
rev[p] = 0;
lmax[p][d] = rmax[p][d] = mx[p][d] = pr - pl + 1;
L[p] = R[p] = d;
lmax[p][d ^ 1] = rmax[p][d ^ 1] = mx[p][d ^ 1] = 0;
sum[p][d] = pr - pl + 1;
sum[p][d ^ 1] = 0;
}
void addRev(int p,int pl,int pr) {
if(cov[p] != -1) cov[p] ^= 1;
rev[p] ^= 1;
swap(lmax[p][0],lmax[p][1]);
swap(rmax[p][0],rmax[p][1]);
swap(mx[p][0],mx[p][1]);
swap(sum[p][0],sum[p][1]);
L[p] ^= 1;
R[p] ^= 1;
}
void push_down(int p,int pl,int pr) {
if(rev[p]) {
addRev(ls,pl,mid);
addRev(rs,mid+1,pr);
rev[p] = 0;
}
if(cov[p] != -1) {
addCov(ls,pl,mid,cov[p]);
addCov(rs,mid+1,pr,cov[p]);
cov[p] = -1;
}
}
void Cov(int p,int pl,int pr,int l,int r,int d){
if(l <= pl && pr <= r) {addCov(p,pl,pr,d);return;}
push_down(p,pl,pr);
if(l <= mid) Cov(ls,pl,mid,l,r,d);
if(r > mid) Cov(rs,mid+1,pr,l,r,d);
push_up(p,pl,pr);
}
void Rev(int p,int pl,int pr,int l,int r){
if(l <= pl && pr <= r) {addRev(p,pl,pr);return;}
push_down(p,pl,pr);
if(l <= mid) Rev(ls,pl,mid,l,r);
if(r > mid) Rev(rs,mid+1,pr,l,r);
push_up(p,pl,pr);
}
int askSum(int p,int pl,int pr,int l,int r){
if(l <= pl && pr <= r) {return sum[p][1];}
push_down(p,pl,pr);
int res = 0;
if(l <= mid) res += askSum(ls,pl,mid,l,r);
if(r > mid) res += askSum(rs,mid+1,pr,l,r);
return res;
}
node cn(int p,int pl,int pr,int l,int r){
if(l <= pl && pr <= r) {return node(L[p],R[p],lmax[p][1],rmax[p][1],mx[p][1],sum[p][1]);}
push_down(p,pl,pr);
if(l > mid) return cn(rs,mid+1,pr,l,r);
else if(r <= mid) return cn(ls,pl,mid,l,r);
else {
node a = cn(ls,pl,mid,l,r),b = cn(rs,mid+1,pr,l,r),c;
c.lmax = a.lmax,c.rmax = b.rmax;
c.sum = a.sum + b.sum;
c.mx = max(a.mx,b.mx);
c.l = a.l,c.r = b.r;
if(b.l == a.r && a.r == 1) {
if(a.sum == mid - pl + 1) c.lmax += b.lmax;
if(b.sum == pr - mid) c.rmax += a.rmax;
c.mx = max(c.mx,a.rmax + b.lmax);
}
return c;
}
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr),cout.tie(nullptr);
int opt,l,r;
cin>>n>>m;
for(int i = 1;i<=n;i++) cin>>a[i];
sgm::build(1,1,n);
while(m--) {
cin>>opt>>l>>r;
l++,r++;
switch(opt) {
case 0:
sgm::Cov(1,1,n,l,r,0);
break;
case 1:
sgm::Cov(1,1,n,l,r,1);
break;
case 2:
sgm::Rev(1,1,n,l,r);
break;
case 3:
cout<<sgm::askSum(1,1,n,l,r)<<'\n';
break;
case 4:
cout<<sgm::cn(1,1,n,l,r).mx<<'\n';
break;
}
}
return 0;
}
2024/07/11
校内模拟赛 #2
A.弹钢琴
上一次写 d p dp dp 还是在上一次
最近几天,一直在写数据结构
d
p
dp
dp 我是一点没练,成功在赛时精神不振,萎靡不振,做到了签到题耗时
3
h
3h
3h 的 好成绩
这里附上我当天的运势

题面:
题目背景
PianoEater喜欢听钢琴曲,并且一直梦想着给他的GF Little Pink弹奏一曲。于是PianoEater去钢琴王国大学(Piano Kingdom University,简称PKU)找钢琴十级的rainbow学习弹琴。
PianoEater弹琴时,他的一只手上的5根手指不能交叉,并且两根手指不能放在同一个琴键上。同时,一只手的大拇指和小指之间最多间隔7个琴键。弹琴时,左右臂可以交叉,但是用(其中一只手的手指)去按(处于另一只手的两个手指之间)的按键是不允许的。题目描述
现在PianoEater有一架有52个白键和36个黑键的钢琴,并且他要弹奏的曲子只需要按白键。在同一时刻,他只用弹奏一个音符。如果这个音符不移动大拇指就可以按到,那么他不需要耗费体力;否则他需要花费sqrt(x)(下取整)的体力来移动手的位置(也就是移动大拇指的位置)。其中x代表移动前后大拇指的位置之差的绝对值。
现在有一首由N个音符组成的乐曲,每个音符用0~51之间的一个整数表示,分别对应了52个白键。0是最左边的键,51是最右边的键。PianoEater想知道他弹完这首曲子最少需要耗费多少体力。
输入格式
输入的第一行是三个整数,L,R,N,分别表示初始时刻左手大拇指的位置、右手大拇指的位置和乐曲的音符数。
接下来N行每行一个在0~51之间的整数,代表需要弹奏的音符。
输出格式
输出一个整数,表示最少需要耗费的体力。
样例 #1
样例输入 #1
10 20 10 0 1 2 3 4 5 6 7 8 9样例输出 #1
2提示
【时间限制】
1s
【题目提示】
对于30%的数据,1<=N<=100
对于50%的数据,1<=N<=500
对于100%的数据,1<=N<=1000,4<=L<=51,0<=R<=47
作为一个 O I e r OIer OIer,我是没想到还要看题面背景,导致我直接错过了重要信息:
PianoEater弹琴时,他的一只手上的5根手指不能交叉,并且两根手指不能放在同一个琴键上。同时,一只手的大拇指和小指之间最多间隔7个琴键。弹琴时,左右臂可以交叉,但是用(其中一只手的手指)去按(处于另一只手的两个手指之间)的按键是不允许的。
警钟长鸣!
直接
d
p
dp
dp 下一个音符,左右手就好了 dp[i][L][R]
因为用什么手指按目标琴键很关键,所以要枚举
右手大拇指位置 → [ x − 8 ∼ x ] 左手大拇指位置 → [ x ∼ x + 8 ] 右手大拇指位置 \rightarrow [x - 8 \sim x] \\ 左手大拇指位置 \rightarrow [x \sim x + 8] 右手大拇指位置→[x−8∼x]左手大拇指位置→[x∼x+8]
然后转移式
l e f t − h a n d : f i , x + l , k ← f i − 1 , j , k + ∣ j − ( x + l ) ∣ left-hand:\ f_{i,x + l,k} \leftarrow f_{i-1,j,k} + \sqrt{\lvert j - (x + l) \rvert} left−hand: fi,x+l,k←fi−1,j,k+∣j−(x+l)∣
r i g h t − h a n d : f i , j , x − l ← f i − 1 , j , k + ∣ ( x − l ) − k ∣ right-hand:\ f_{i,j,x - l} \leftarrow f_{i-1,j,k} + \sqrt{\lvert (x - l) - k \rvert} right−hand: fi,j,x−l←fi−1,j,k+∣(x−l)−k∣
注意题面背景,加上
左手条件:if(x + l < k || x + l - 5 > k + 5)
右手条件:if(j < x - l || x - l + 5 < j - 5)
就大功告成了
AC-code:
#include<bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 1e3 + 5,inf = 0x3f3f3f3f;
int dp[N][60][60];
signed main() {
memset(dp,0x3f,sizeof(dp));
int L = rd(),R = rd(),n = rd();
dp[0][L][R] = 0;
for(int i = 1;i<=n;i++) {
int x = rd();
for(int j = 0;j<=51;j++)
for(int k = 0;k <= 51;k++) if(dp[i-1][j][k] != inf){
for(int l = 0;l<=8;l++) if(x + l < k || x + l - 5 > k + 5) dp[i][x + l][k] = min(dp[i][x + l][k],dp[i-1][j][k] + int(sqrt(abs(j - (x + l)))));
for(int l = 0;l<=8;l++) if(j < x - l || x - l + 5 < j - 5) dp[i][j][x - l] = min(dp[i][j][x - l],dp[i-1][j][k] + int(sqrt(abs((x - l) - k))));
}
}
int ans = inf;
for(int i = 0;i<=51;i++) for(int j = 0;j<=51;j++) ans = min(ans,dp[n][i][j]);
wt(ans);
return 0;
}
B.捉迷藏
被骗了,这不是搜索
题面:
题目背景
vani和cl2在一片树林里捉迷藏……
这片树林里有N座房子,M条有向道路,组成了一张有向无环图。
树林里的树非常茂密,足以遮挡视线,但是沿着道路望去,却是视野开阔。如果从房子A沿着路走下去能够到达B,那么在A和B里的人是能够相互望见的。题目描述
现在cl2要在这N座房子里选择K座作为藏身点,同时vani也专挑cl2作为藏身点的房子进去寻找,为了避免被vani看见,cl2要求这K个藏身点的任意两个之间都没有路径相连。
为了让vani更难找到自己,cl2想知道最多能选出多少个藏身点?输入格式
第一行两个整数N,M。
接下来M行每行两个整数x、y,表示一条从x到y的有向道路。
输出格式
一个整数K,表示最多能选取的藏身点个数。
样例 #1
样例输入 #1
4 4 1 2 3 2 3 4 4 2样例输出 #1
2提示
【时间限制】
1s
【题目提示】
对于20% 的数据,N≤10,M<=20。
对于60% 的数据, N≤100,M<=1000。
对于100% 的数据,N≤200,M<=30000,1<=x,y<=N。
不难想到传递闭包,判断两点之间的连通性
但是接下来就不好办了,如果暴搜,只有 75 75 75 分,让人很不愉快
然而题解是 二分图最大匹配 → \rightarrow → 最小点覆盖集
连通的两点 i , j i,j i,j 就 i → j + N i \rightarrow j + N i→j+N 建边 和 j + N → i j + N \rightarrow i j+N→i 建边
这样就可以让每一个连通的部分只有一个被加入答案
这题对于我这个没怎么写过二分图匹配的不大友好
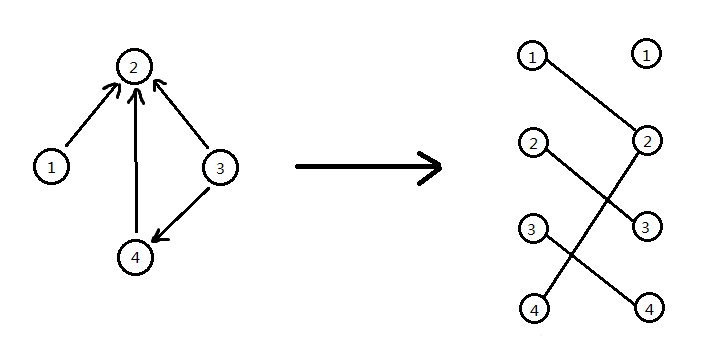
找最小点覆盖集就可以了,方法是:
最小点覆盖集 = 二分图点数 − 二分图最大匹配 最小点覆盖集 = 二分图点数 - 二分图最大匹配 最小点覆盖集=二分图点数−二分图最大匹配
AC-code:
#include<bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 205;
bool G[N][N];
vector<int> g[N << 1];
int mch[N << 1],vis[N<<1];
bool dfs(const int u,const int tag) {
if(vis[u] == tag) return false;
vis[u] = tag;
for(int v:g[u]) if((mch[v] == 0)||dfs(mch[v],tag)){
mch[v] = u;
return true;
}
return false;
}
signed main() {
int n = rd(),m = rd();
for(int i = 1;i<=m;i++) {
int u = rd(),v = rd();
G[u][v] = 1;
}
for(int k = 1;k<=n;k++)
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
G[i][j] = G[i][j] | (G[i][k] & G[k][j]);
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
if(G[i][j]) {
g[i].push_back(j + N);
g[j + N].push_back(i);
}
int ans = 0;
for(int i = 1;i<=n;i++) ans += dfs(i,i);
wt(n - ans);
return 0;
}
C.水叮当的舞步
或者是打开这个 UVA1505 Flood-it!
神仙 I D A ∗ IDA* IDA∗ 题
估价函数为在场的剩余颜色种类
int F() {
int t = 0;
memset(f,0,sizeof(f));
for(int i = 1;i<=n;i++) {
for(int j = 1;j<=n;j++) {
if(!f[m[i][j]] && v[i][j] ^ 1){
f[m[i][j]] = 1;
t++;
}
}
}
return t;
}
确定周围位置
void paint(int x,int y,int c){
v[x][y] = 1;
for(int i = 1;i<=4;i++) {
int tx = x + d[i][0],ty = y + d[i][1];
if((!check(tx,ty)) || v[tx][ty] == 1) continue;
v[tx][ty] = 2;
if(m[tx][ty] == c) paint(tx,ty,c);
}
}
枚举每种颜色,以左上角为起点向周围染色,
int fill(int c) {
int t = 0;
for(int i = 1;i<=n;i++) {
for(int j = 1;j<=n;j++) {
if(m[i][j] == c && v[i][j] == 2) {
t++;
paint(i,j,c);
}
}
}
return t;
}
迭代加深搜索 AC-code:
#include<bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
#define check(x,y) ((x) >= 1 && (x) <= n && (y) >= 1 && (y) <= n)
const int N = 10;
int n;
int d[5][2] = {{0,0},{0,1},{1,0},{-1,0},{0,-1}};
int m[N][N],v[N][N],f[N];
int F() {
int t = 0;
memset(f,0,sizeof(f));
for(int i = 1;i<=n;i++) {
for(int j = 1;j<=n;j++) {
if(!f[m[i][j]] && v[i][j] ^ 1){
f[m[i][j]] = 1;
t++;
}
}
}
return t;
}
void paint(int x,int y,int c){
v[x][y] = 1;
for(int i = 1;i<=4;i++) {
int tx = x + d[i][0],ty = y + d[i][1];
if((!check(tx,ty)) || v[tx][ty] == 1) continue;
v[tx][ty] = 2;
if(m[tx][ty] == c) paint(tx,ty,c);
}
}
int fill(int c) {
int t = 0;
for(int i = 1;i<=n;i++) {
for(int j = 1;j<=n;j++) {
if(m[i][j] == c && v[i][j] == 2) {
t++;
paint(i,j,c);
}
}
}
return t;
}
int rule;
bool dfs(int dep) {
int g = F();
if(dep + g > rule) return false;
if(!g) return true;
int rec[10][10];
for(int i = 0;i<=5;i++) {
memcpy(rec,v,sizeof(v));
if(fill(i) && dfs(dep + 1)) return true;
memcpy(v,rec,sizeof(rec));
}
return false;
}
signed main() {
while(1){
memset(v,0,sizeof(v));
n = rd();
if(n == 0) break;
for(int i = 1;i<=n;i++) for(int j = 1;j<=n;j++) m[i][j] = rd();
paint(1,1,m[1][1]);
for(rule = 0;;rule++) if(dfs(0)) break;
wt(rule);
putchar('\n');
}
return 0;
}
P5664 [CSP-S2019] Emiya 家今天的饭
《深进》例题
题面:
题目描述
Emiya 是个擅长做菜的高中生,他共掌握 n n n 种烹饪方法,且会使用 m m m 种主要食材做菜。为了方便叙述,我们对烹饪方法从 1 ∼ n 1 \sim n 1∼n 编号,对主要食材从 1 ∼ m 1 \sim m 1∼m 编号。
Emiya 做的每道菜都将使用恰好一种烹饪方法与恰好一种主要食材。更具体地,Emiya 会做 a i , j a_{i,j} ai,j 道不同的使用烹饪方法 i i i 和主要食材 j j j 的菜( 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n、 1 ≤ j ≤ m 1 \leq j \leq m 1≤j≤m),这也意味着 Emiya 总共会做 ∑ i = 1 n ∑ j = 1 m a i , j \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m} a_{i,j} i=1∑nj=1∑mai,j 道不同的菜。
Emiya 今天要准备一桌饭招待 Yazid 和 Rin 这对好朋友,然而三个人对菜的搭配有不同的要求,更具体地,对于一种包含 k k k 道菜的搭配方案而言:
- Emiya 不会让大家饿肚子,所以将做至少一道菜,即 k ≥ 1 k \geq 1 k≥1
- Rin 希望品尝不同烹饪方法做出的菜,因此她要求每道菜的烹饪方法互不相同
- Yazid 不希望品尝太多同一食材做出的菜,因此他要求每种主要食材至多在一半的菜(即 ⌊ k 2 ⌋ \lfloor \frac{k}{2} \rfloor ⌊2k⌋ 道菜)中被使用
这里的 ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋ 为下取整函数,表示不超过 x x x 的最大整数。
这些要求难不倒 Emiya,但他想知道共有多少种不同的符合要求的搭配方案。两种方案不同,当且仅当存在至少一道菜在一种方案中出现,而不在另一种方案中出现。
Emiya 找到了你,请你帮他计算,你只需要告诉他符合所有要求的搭配方案数对质数 998 , 244 , 353 998,244,353 998,244,353 取模的结果。
输入格式
第 1 行两个用单个空格隔开的整数 n , m n,m n,m。
第 2 行至第 n + 1 n + 1 n+1 行,每行 m m m 个用单个空格隔开的整数,其中第 i + 1 i + 1 i+1 行的 m m m 个数依次为 a i , 1 , a i , 2 , ⋯ , a i , m a_{i,1}, a_{i,2}, \cdots, a_{i,m} ai,1,ai,2,⋯,ai,m。
输出格式
仅一行一个整数,表示所求方案数对 998 , 244 , 353 998,244,353 998,244,353 取模的结果。
样例 #1
样例输入 #1
2 3 1 0 1 0 1 1样例输出 #1
3样例 #2
样例输入 #2
3 3 1 2 3 4 5 0 6 0 0样例输出 #2
190样例 #3
样例输入 #3
5 5 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 1 0 1 0 1 0 1 1 0 1样例输出 #3
742提示
【样例 1 解释】
由于在这个样例中,对于每组 i , j i, j i,j,Emiya 都最多只会做一道菜,因此我们直接通过给出烹饪方法、主要食材的编号来描述一道菜。
符合要求的方案包括:
- 做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 2 的菜
- 做一道用烹饪方法 1、主要食材 1 的菜和一道用烹饪方法 2、主要食材 3 的菜
- 做一道用烹饪方法 1、主要食材 3 的菜和一道用烹饪方法 2、主要食材 2 的菜
因此输出结果为 3 m o d 998 , 244 , 353 = 3 3 \bmod 998,244,353 = 3 3mod998,244,353=3。 需要注意的是,所有只包含一道菜的方案都是不符合要求的,因为唯一的主要食材在超过一半的菜中出现,这不满足 Yazid 的要求。
【样例 2 解释】
Emiya 必须至少做 2 道菜。
做 2 道菜的符合要求的方案数为 100。
做 3 道菜的符合要求的方案数为 90。
因此符合要求的方案数为 100 + 90 = 190。
【数据范围】
测试点编号 n = n= n= m = m= m= a i , j < a_{i,j}< ai,j< 测试点编号 n = n= n= m = m= m= a i , j < a_{i,j}< ai,j< 1 1 1 2 2 2 2 2 2 2 2 2 7 7 7 10 10 10 2 2 2 1 0 3 10^3 103 2 2 2 2 2 2 3 3 3 2 2 2 8 8 8 10 10 10 3 3 3 1 0 3 10^3 103 3 3 3 5 5 5 2 2 2 2 2 2 9 ∼ 12 9\sim 12 9∼12 40 40 40 2 2 2 1 0 3 10^3 103 4 4 4 5 5 5 3 3 3 2 2 2 13 ∼ 16 13\sim 16 13∼16 40 40 40 3 3 3 1 0 3 10^3 103 5 5 5 10 10 10 2 2 2 2 2 2 17 ∼ 21 17\sim 21 17∼21 40 40 40 500 500 500 1 0 3 10^3 103 6 6 6 10 10 10 3 3 3 2 2 2 22 ∼ 25 22\sim 25 22∼25 100 100 100 2 × 1 0 3 2\times 10^3 2×103 998244353 998244353 998244353 对于所有测试点,保证 1 ≤ n ≤ 100 1 \leq n \leq 100 1≤n≤100, 1 ≤ m ≤ 2000 1 \leq m \leq 2000 1≤m≤2000, 0 ≤ a i , j < 998 , 244 , 353 0 \leq a_{i,j} \lt 998,244,353 0≤ai,j<998,244,353。
首先,我们不急着考虑全部 3 3 3 个要求,先试着考虑前两个要求,
对于任意一种烹饪方法 i i i,选择的菜数取值在 [ 0 ∼ ∑ j = 1 m a i , j ] [0 \sim \sum_{j = 1}^{m} a_{i,j}] [0∼∑j=1mai,j] 之中,共 1 + ∑ j = 1 m a i , j 1 + \sum_{j = 1}^{m} a_{i,j} 1+∑j=1mai,j 种选择。
对于整体,则有
∏
i
=
1
n
(
1
+
∑
j
=
1
m
a
i
,
j
)
\prod_{i = 1}^n (1 + \sum_{j = 1}^m a_{i,j})
∏i=1n(1+∑j=1mai,j) 中选择,但是我们不能让所有人饿肚子,故方案总数为
[
∏
i
=
1
n
(
1
+
∑
j
=
1
m
a
i
,
j
)
]
−
1
[\prod_{i = 1}^n (1 + \sum_{j = 1}^m a_{i,j})] - 1
[i=1∏n(1+j=1∑mai,j)]−1
然后,割去不满足第 3 3 3 种情况的方案
我们设 f i , k , c f_{i,k,c} fi,k,c 为 前 i i i 种烹饪方式,选择了 k k k 种菜品,其中第 x x x 种菜品拿了 c c c 个的方案数
不难有转移:
f
i
,
k
,
c
←
[
j
=
x
]
f
i
−
1
,
j
−
1
,
c
−
1
⋅
a
i
,
j
f
i
,
k
,
c
←
[
j
≠
x
]
f
i
−
1
,
j
−
1
,
c
⋅
a
i
,
j
f
i
,
k
,
c
←
n
o
t
h
i
n
g
h
a
p
p
e
n
e
d
f
i
−
1
,
j
,
c
\large f_{i,k,c} \leftarrow^{[j = x]} f_{i-1,j-1,c-1} \cdot a_{i,j} \\ \large f_{i,k,c} \leftarrow^{[j \not = x]} f_{i-1,j-1,c} \cdot a_{i,j}\\ \large f_{i,k,c} \leftarrow^{nothing\ happened} f_{i-1,j,c}
fi,k,c←[j=x]fi−1,j−1,c−1⋅ai,jfi,k,c←[j=x]fi−1,j−1,c⋅ai,jfi,k,c←nothing happenedfi−1,j,c
很遗憾,我们要枚举 i , k , c , x i,k,c,x i,k,c,x,完美的来到了 O ( m n 3 ) O(mn^3) O(mn3),不能接受
我们要开启人类智慧,放缩优化状态
我们有 c > ⌊ k 2 ⌋ , c c > \lfloor \frac{k}{2} \rfloor,c c>⌊2k⌋,c 是一个整数
那么,
c
>
⌊
k
2
⌋
⇒
k
∈
o
d
d
c
>
k
2
−
1
2
⇒
2
c
+
1
>
k
c > \lfloor \frac{k}{2} \rfloor \Rightarrow^{k \in odd} c > \frac{k}{2} - \frac{1}{2} \Rightarrow 2c + 1 > k
c>⌊2k⌋⇒k∈oddc>2k−21⇒2c+1>k
c > ⌊ k 2 ⌋ ⇒ k ∈ e v e n c > k 2 ⇒ 2 c > k c > \lfloor \frac{k}{2} \rfloor \Rightarrow^{k \in even} c > \frac{k}{2} \Rightarrow 2c > k c>⌊2k⌋⇒k∈evenc>2k⇒2c>k
k ∈ o d d k \in odd k∈odd 时,由于 2 c + 1 ∈ o d d 2c + 1 \in odd 2c+1∈odd,那么 2 c ≥ k + 1 2c \geq k + 1 2c≥k+1,所以 c > k 2 ⇒ 2 c > k c > \frac{k}{2} \Rightarrow 2c > k c>2k⇒2c>k
所以, 2 c > k → 2 c − k > 0 2c > k \rightarrow 2c - k > 0 2c>k→2c−k>0
然后让我们变换一下,得到 c − ( k − c ) > 0 c - (k - c) > 0 c−(k−c)>0
这个式子的含义是不符合条件的方案必须满足 超过一半总数的菜品 − 剩下的菜品 > 0 超过一半总数的菜品 - 剩下的菜品 > 0 超过一半总数的菜品−剩下的菜品>0(虽然很显然,但是还是用理论推导了一遍),
那么我们最后只要关注这个 Δ = 超过一半总数的菜品 − 剩下的菜品 > 0 \Delta = 超过一半总数的菜品 - 剩下的菜品 > 0 Δ=超过一半总数的菜品−剩下的菜品>0 的方案数,累加即可得到所有不符合条件的方案数
那么,我们重新设 f i , Δ f_{i,\Delta} fi,Δ
有转移:
f
i
,
Δ
+
1
←
j
=
x
a
i
,
j
⋅
f
i
−
1
,
Δ
f_{i,\Delta + 1} \leftarrow^{j = x} a_{i,j} \cdot f_{i-1,\Delta}
fi,Δ+1←j=xai,j⋅fi−1,Δ
f
i
,
Δ
−
1
←
j
≠
x
a
i
,
j
⋅
f
i
−
1
,
Δ
f_{i,\Delta - 1} \leftarrow^{j \not= x} a_{i,j}\cdot f_{i-1,\Delta}
fi,Δ−1←j=xai,j⋅fi−1,Δ
最后注意 Δ \Delta Δ 会是负数,扩大一倍去维护就好了
结束!
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 105,M = 2e3+5;
const int mod = 998244353;
int S[N],d[N][M],dp[N][N<<1];
signed main() {
int n = rd(),m = rd();
int prod = 1;
for(int i = 1;i<=n;i++) {
for(int j = 0;j<m;j++) {
d[i][j] = rd();
S[i] = (S[i] + d[i][j]) % mod;
}
prod = 1ll * prod * (S[i] + 1) % mod;
}
int ans = (prod + mod - 1) % mod;
for(int x = 0;x < m;x++) {
memset(dp,0,sizeof(dp));
dp[0][0 + 101] = 1;
int no = 0;
for(int i = 1;i<=n;i++) {
int re = (S[i] + mod - d[i][x]) % mod;
for(int dt = 1;dt <= 201;dt++) {
dp[i][dt + 1] = (dp[i][dt + 1] + 1ll * dp[i-1][dt] * d[i][x] % mod) % mod;
dp[i][dt - 1] = (dp[i][dt - 1] + 1ll * dp[i-1][dt] * re % mod) % mod;
dp[i][dt] = (dp[i][dt] + dp[i-1][dt]) % mod;
}
}
for(int dt = 1;dt<=n;dt++) no = (no + dp[n][dt + 101]) % mod;
ans = (ans + mod - no) % mod;
}
wt(ans);
return 0;
}























 343
343

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








