2024.7 - 做题记录与方法总结 - Part 4

最新推荐文章于 2024-08-21 17:23:27 发布

MingJunYi

最新推荐文章于 2024-08-21 17:23:27 发布

阅读量511

点赞数 16

分类专栏：做题记录与方法总结文章标签：算法 c++ 笔记其他

本文链接：https://blog.csdn.net/qq_49785217/article/details/141390655

版权

做题记录与方法总结专栏收录该内容

9 篇文章 0 订阅

订阅专栏

2024/07/23

梦熊题单

E.基础数据结构题

给定一个长度为的序列，下标从开始，你需要维护三种操作：

对于，令。

对于，求的和。

本题来自 $UOJ\ #228$

这里是李欣隆的课件：

sqrt这个操作肯定是一个均摊，因为下降很快
但是有区间加，怎么办呢
想一想感觉可以维护值相同的连续段试试？

带修的势能线段树！

我们要发现，当区间每一个值都相等时 $\rightarrow \sqrt{x} \Rightarrow x + (sqrt(x) - x)$ ，
那么就把区间根号的修改变成了区间加
然后就结束了…吗？

我们发现这样肯定有毛病

然后就TLE了
发现会被奇怪的数据卡
比如3 4 3 4 3 4
开sqrt后变成1 2 1 2 1 2
然后加2又变成3 4 3 4 3 4
Oh no！

发现这种情况仅当 $a = b - 1$ 且 $b$ 是完全平方数的时候会出现
于是想办法维护一下区间极差就可以判掉这种情况
由于取sqrt的次数是 $\log\log v )$ 的
所以总复杂度是 $(n+m)\log n \log \log v )$
大概是使用所有连续段以外相邻位置的差来作为势能的均摊

AC-code（没有维护 $a = b - 1$ 的情况，因为数据范围太小了，无论如何构造都能过原题）：

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 1e5+5; 

int n,m,a[N];

namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)

int t[N<<2],tag[N<<2],mx[N<<2],mn[N<<2],ts[N<<2];

void push_up(int p) {
    t[p] = t[ls] + t[rs];
    mx[p] = max(mx[ls],mx[rs]);
    mn[p] = min(mn[ls],mn[rs]);
}

void build(int p,int pl,int pr) {
    if(pl == pr) {t[p] = mx[p] = mx[p] = a[pl]; return;}
    build(ls,pl,mid);
    build(rs,mid+1,pr);
    push_up(p);
}

void addtag(int p,int pl,int pr,int k) {
    t[p] += (pr - pl + 1) * k;
    tag[p] += k;
    mx[p] += k;
    mn[p] += k;
} 

void push_down(int p,int pl,int pr) {
    if(tag[p]) {
        addtag(ls,pl,mid,tag[p]);
        addtag(rs,mid+1,pr,tag[p]);
        tag[p] = 0;
    }
}

void update(int p,int pl,int pr,int l,int r,int d) {
    if(l <= pl && pr <= r) {addtag(p,pl,pr,d);return;}
    push_down(p,pl,pr);
    if(l <= mid) update(ls,pl,mid,l,r,d);
    if(r > mid) update(rs,mid+1,pr,l,r,d);
    push_up(p);
}

void getsqrt(int p,int pl,int pr,int l,int r) {
    if(pl == pr) {mx[p] = mn[p] = t[p] = sqrt(t[p]);return;}
    int maxx = (int)sqrt(mx[p]) - mx[p],minn = (int)sqrt(mn[p]) - mn[p];//维护值相同的连续段
    if(l <= pl && pr <= r && (maxx == minn || (maxx - minn >= 1 && maxx == (int)sqrt(maxx) * (int)sqrt(maxx)))) {addtag(p,pl,pr,maxx);return;}
    push_down(p,pl,pr);
    if(l <= mid) getsqrt(ls,pl,mid,l,r);
    if(r > mid) getsqrt(rs,mid+1,pr,l,r);
    push_up(p);
}

int query(int p,int pl,int pr,int l,int r) {
    if(l <= pl && pr <= r) return t[p];
    push_down(p,pl,pr);
    int res = 0;
    if(l <= mid) res += query(ls,pl,mid,l,r);
    if(r > mid) res += query(rs,mid+1,pr,l,r);
    return res;
}

}

signed main() {

	n = rd(),m = rd();
    for(int i = 1;i<=n;i++) a[i] = rd();
    sgt::build(1,1,n);
    while(m--) {
        int opt = rd();
        int l,r,x;
        switch (opt)
        {
        case 1:
            l = rd(),r = rd(),x = rd();
            sgt::update(1,1,n,l,r,x);
            break;
        case 2:
            l = rd(),r = rd();
            sgt::getsqrt(1,1,n,l,r);
            break;
        case 3:
            l = rd(),r = rd();
            wt(sgt::query(1,1,n,l,r));
            putchar('\n');
            break;
        default:
            break;
        }
    }

	return 0;
}

求助 Chatgpt 的 SOS-dp 帮助：

算法竞赛中 SOS 是什么？

在算法竞赛中，SOS 通常指的是 “Sum Over Subsets” 技术。SOS 技术是一种用于高效计算涉及子集的问题的动态规划方法，特别是在处理诸如子集>和、子集数目等方面的运算时非常有用。

SOS 动态规划的基本思想

假设你有一个大小为 ($ n $) 的集合 $\{0, 1, 2, \ldots, n-1\} )$ ，我们定义一个函数 ( f(S) )，其中 ( S ) 是该集合的一个子集。>我们的目标是计算每个子集 ( S ) 的某种函数值的和，这种和可以表示为：

$g(S) = \sum_{T \subseteq S} f(T) $

基本例子

假设我们有一个数组 ( f )，其中每个元素 ( f[S] ) 表示子集 ( S ) 的值。我们希望计算每个子集 ( S ) 的所有子集的值的和 ( g(S) >)。

递推公式

我们可以使用以下递推公式来计算 ( g(S) )：

$ g(S) = \sum_{T \subseteq S} f(T) $

通过动态规划，我们可以通过处理每个子集 ( S ) 以及其补集 ( \overline{S} ) 中的每一位来高效地计算 ( g(S) )。

实现步骤

初始化：定义一个数组 ( g ) 来存储结果，并初始化 ( g[S] = f[S] )。
迭代处理每一位：对于每一个可能的子集，迭代处理每一位。如果某一位在当前子集 ( S ) 中是未设置的（即该位为 0），则我们将其设置>为 1，并更新相应的 ( g ) 值。

示例代码

以下是用 C++ 实现 SOS 动态规划的示例代码：

#include <iostream>
#include <vector>
using namespace std;

void sos_dp(vector<int>& f, int n) {
    vector<int> g = f;

    for (int i = 0; i < n; ++i) {
        for (int mask = 0; mask < (1 << n); ++mask) {
            if (mask & (1 << i)) {
                g[mask] += g[mask ^ (1 << i)];
            }
        }
    }

    for (int mask = 0; mask < (1 << n); ++mask) {
        cout << "g[" << mask << "] = " << g[mask] << endl;
    }
}

int main() {
    int n = 3;
    vector<int> f(1 << n);

    // Define your f function here, e.g., f(S) = S
    for (int i = 0; i < (1 << n); ++i) {
        f[i] = i;  // Example function: f(S) = S
    }

    sos_dp(f, n);

    return 0;
}

解释

初始化：g 数组初始化为 f。
迭代处理每一位：

遍历每一位 (i)。
对于每个可能的子集 mask，如果第 (i) 位在 mask 中设置（即 mask \& (1 << i) 为真），则更新 g[mask] 的值。

最终，g 数组将包含每个子集 (S) 的所有子集的和。

复杂度

这个算法的时间复杂度为 $\cdot 2^n))$ ，其中 (n) 是集合的大小。这是因为我们需要处理每个子集，并且对每一位进行更新。尽管看起来复>杂，但对于小规模的问题（如 ( $\leq 20$ )），这是一个非常高效的算法。

2024/07/24

A. 最短路(package)

给定一个包含个节点和条边的图，每条边有一个权值。

你的任务是回答个询问，每个询问包含两个正整数和表示起点和终点，要求寻找从到的一条路径，使得路径上权值最大的一条边权值最小。

接下来行，每行三个整数 , 表示一个由到的长度为的双向边。

再接下来行，每行两个整数，表示询问从连接到的所有路径中单边长度最大值的最小值。

另外，如果到没有路径相连通，输出 -1 即可。

30
-1
30

此题写全源最短路？ $\leq 1000,m \leq 10000,k \leq 1000$ 不允许

那么我们就得换一种方式思考，最小值 & 连通

请想到 最小生成树，这就是答案！

我们对每一颗连通块建最小生成树（类似与货车运输）

如何对每一次询问，判断是否在同一颗生成树，然后暴力求 $\rightsquigarrow t$ 的路径上的最大值

AC-code:

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 1e3+5,M = 1e5+5;

int n,m,k;
struct Edge{
	int u,v,w;
}edge[M<<1];

int s[N<<1],cnt;
bool cmp(const Edge &a,const Edge &b) { return a.w < b.w;}

int find(int x){
	if(x != s[x]) s[x] = find(s[x]);
	return s[x];
}

int head[N],nxt[M<<1],to[M<<1],idx,val[M<<1];

void init(){memset(head,-1,sizeof(head));}

void add(int u,int v,int w) {
    nxt[idx] = head[u];
    to[idx] = v;val[idx] = w;
    head[u] = idx++;
}

void kru(){
	sort(edge+1,edge+1+m,cmp);
	int f1,f2;
	for(int i = 1;i<=n;i++) s[i] = i;
	for(int i = 1;i<=m;i++) {
		f1 = find(edge[i].u);
		f2 = find(edge[i].v);
		if(f1 != f2) {
            add(edge[i].u,edge[i].v,edge[i].w);
            add(edge[i].v,edge[i].u,edge[i].w);
			s[f1] = f2;
			cnt++;
			if(cnt == n-1) break;
		}
	}
}

int dep[N],e[N],fa[N];

void dfs1(int x,int f) {
    dep[x] = dep[f] + 1;
    fa[x] = f;
    for(int i = head[x];~i;i = nxt[i]) {
        int y = to[i];
        if(y ^ f) {
            e[y] = val[i];
            dfs1(y,x);
        }
    }
}

int find_path(int s,int t) {
    int ans = 0;
    while(s != t) {
        if(dep[s] <= dep[t]) swap(s,t);
        ans = max(ans,e[s]);
        s = fa[s];
    }
    return ans;
}

signed main() {
	init();
    n = rd(),m = rd(),k = rd();
    for(int i = 1;i<=m;i++) {
        int u = rd(),v = rd(),w = rd();
        edge[i].u = u;
        edge[i].v = v;
        edge[i].w = w;
    }

    kru();

    for(int i = 1;i<=n;i++) if(!dep[i]) dfs1(i,0);

    while(k--) {
        int s = rd(),t = rd();
        if(find(s) ^ find(t)) {
            wt(-1);putchar('\n');
            continue;
        }
        wt(find_path(s,t));
        putchar('\n');
    }
	return 0;
}

Lomsat gelral

线段树合并练习题

我们怎么解决问题呢？

寻找众数，自然是 权值线段树 & 线段树上二分

对每一个节点，构造一颗权值线段树，先将本节点权值添加到本节点线段树上

然后将子树的线段树都合并到本节点上（以一种从下到上的合并对每一个节点进行合并）

然后进行查询答案（因为查询是全局的，所以只有查询根节点就可以了）

AC-code:

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 1e5+5;

int head[N],nxt[N<<1],to[N<<1],cnt;

void init(){memset(head,-1,sizeof(head));}

void add(int u,int v) {
	nxt[cnt] = head[u];
	to[cnt] = v;
	head[u] = cnt++;
}

int n,a[N],root[N];

int ls[N * 50],rs[N * 50],ans[N],sum[N * 50],typ[N * 50],A[N * 50],idx;

#define mid ((pl + pr) >> 1)

void push_up(int p) {
	if(sum[ls[p]] < sum[rs[p]]) {
		sum[p] = sum[rs[p]];
		typ[p] = typ[rs[p]];
		A[p] = A[rs[p]];
	}else if(sum[ls[p]] > sum[rs[p]]) {
		sum[p] = sum[ls[p]];
		typ[p] = typ[ls[p]];
		A[p] = A[ls[p]];
	}else{
		sum[p] = sum[ls[p]];
		typ[p] = typ[ls[p]];
		A[p] = A[ls[p]] + A[rs[p]];
	}
}

void update(int &p,int pl,int pr,int k) {
	if(!p) p = ++idx;
	if(pl == pr) {
		sum[p]++;
		typ[p] = k;
		A[p] = k;
		return;
	}
	if(k <= mid) update(ls[p],pl,mid,k);
	else update(rs[p],mid+1,pr,k);
	push_up(p);
}

int merge(int x,int y,int pl,int pr) {
	if(!x || !y) return x + y;
	if(pl == pr) {sum[x] += sum[y];return x;}
	ls[x] = merge(ls[x],ls[y],pl,mid);
	rs[x] = merge(rs[x],rs[y],mid+1,pr);
	push_up(x);
	return x;
}

void dfs(int x,int f) {
	update(root[x],1,N,a[x]);
	for(int i = head[x];~i;i = nxt[i]) {
		int y = to[i];
		if(y ^ f){
			dfs(y,x);
			root[x] = merge(root[x],root[y],1,N);
		}
	}
	ans[x] = A[root[x]];
}

signed main() {
	
	init();
	n = rd();
	for(int i = 1;i<=n;i++) a[i] = rd();
	for(int i = 1;i<n;i++) {
		int u = rd(),v = rd();
		add(u,v);add(v,u);
	}
	dfs(1,0);
	for(int i = 1;i<=n;i++) wt(ans[i]),putchar(' ');

	return 0;
}

2024/07/26

Tourists

题面：

Tourists

题面翻译

Cyberland 有 $n$ 座城市，编号从 $1$ 到 $n$ ，有 $m$ 条双向道路连接这些城市。第 $j$ 条路连接城市 $a_j$ 和 $b_j$ 。每天，都有成千上万的游客来到 Cyberland 游玩。

在每一个城市，都有纪念品售卖，第 $i$ 个城市售价为 $w_i$ 。这个售价有时会变动。

每一个游客的游览路径都有固定起始城市和终止城市，且不会经过重复的城市。

他们会在路径上的城市中，售价最低的那个城市购买纪念品。

你能求出每一个游客在所有合法的路径中能购买的最低售价是多少吗？

你要处理 $q$ 个操作：

C a w：表示 $a$ 城市的纪念品售价变成 $w$ 。

A a b：表示有一个游客要从 $a$ 城市到 $b$ 城市，你要回答在所有他的旅行路径中最低售价的最低可能值。

输入格式

第一行包含用一个空格隔开的三个数 $n, m, q$ 。

接下来 $n$ 行，每行包含一个数 $w_i$ 。

接下来 $m$ 行，每行包含用一个空格隔开的两个数 $a_j$ , $b_j$ 。（ $\le a _ j, b _ j \le n,a _ j \neq b _ j$ ）

数据保证没有两条道路连接同样一对城市，也没有一条道路两端是相同的城市。并且任意两个城市都可以相互到达。

接下来 $q$ 行，每行是 C a w 或 A a b ，描述了一个操作。

输出格式

对于每一个 A 类操作，输出一行表示对应的答案。

样例 #1

样例输入 #1
3 3 3
1
2
3
1 2
2 3
1 3
A 2 3
C 1 5
A 2 3
样例输出 #1
1
2
样例 #2

样例输入 #2
7 9 4
1
2
3
4
5
6
7
1 2
2 5
1 5
2 3
3 4
2 4
5 6
6 7
5 7
A 2 3
A 6 4
A 6 7
A 3 3
样例输出 #2
2
1
5
3

很好很好的 圆方树 + 树剖题

因为对于每一个点双，从任意点出发、任意点结束，都可以找到路径经过指定的点

自然可以想到建圆方树，然后对圆方树树剖

那么，我们只要维护点双中值最小的点即可

修改操作，我们使用multiset用平衡树自动维护最小值，更新时删被修改值，添加更新值和方点值

可以将点双中值最小的点存进方点vector<int>中，然后树剖查路径最小值

然后，我们惊讶的发现 TLE

因为我们会被菊花图卡爆成 $O(n^2)$ ！

我们更自然的观察圆方树

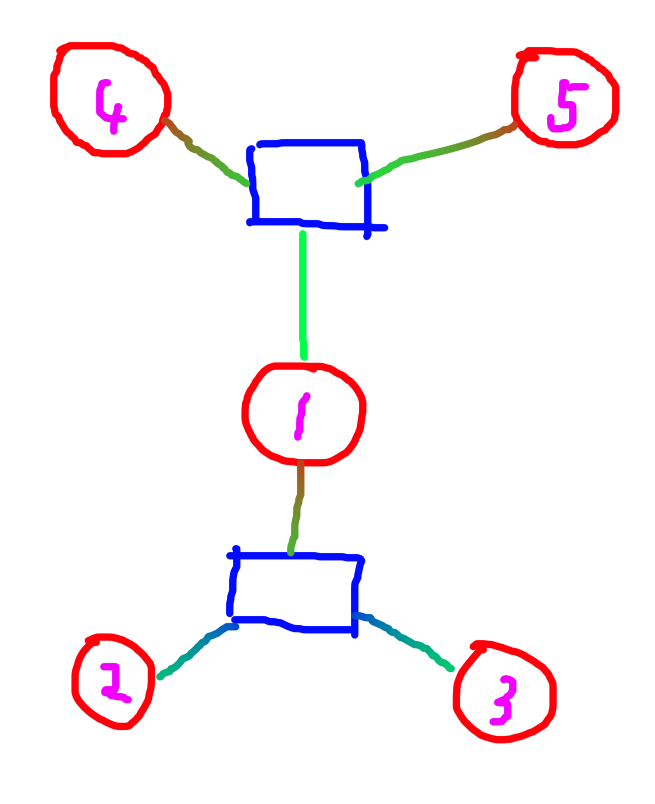
不难发现如 $\sim 3$ 的路径，需要访问节点 $1$ ，而这种节点有且仅有一个，是方点的父亲，如：

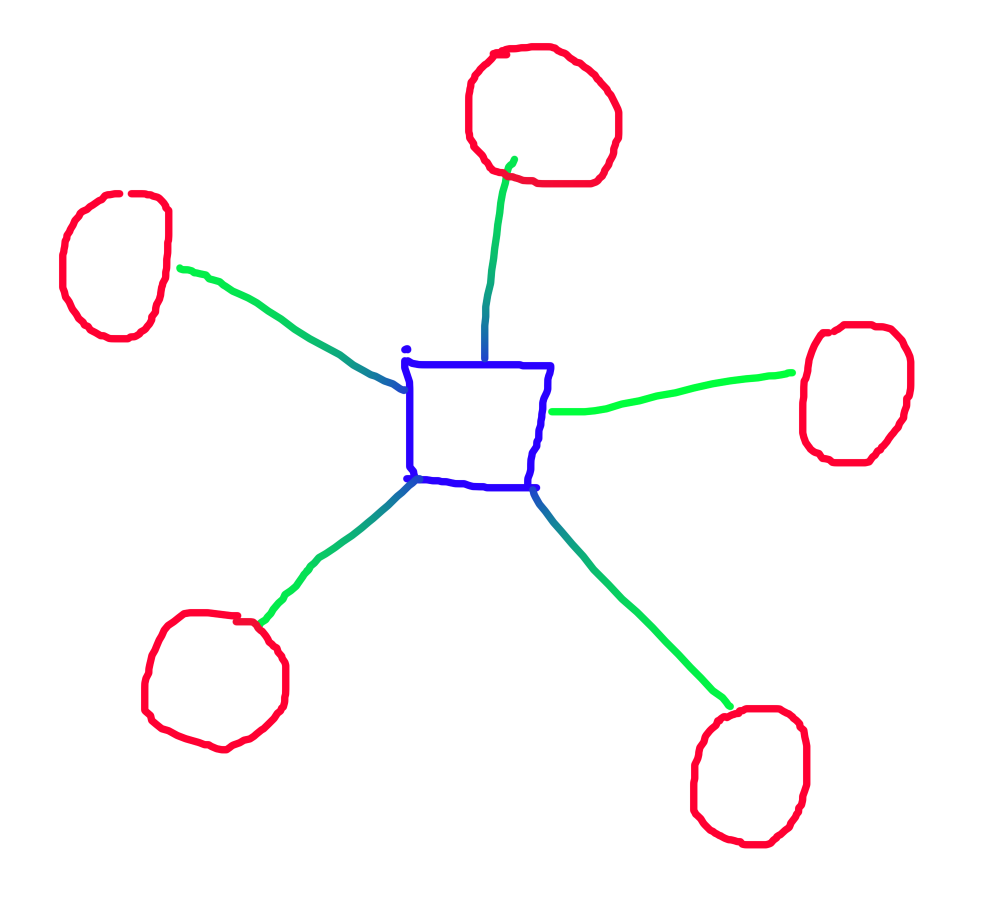
那么我们只需要在询问时对方点的父亲特别查询一下就好了！

AC-code:

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 3e5+5,inf = 1e18;

struct Edge{
int head[N << 1],nxt[N<<1],to[N<<1],cnt;

Edge() {memset(head,-1,sizeof(head));}

void add(int u,int v) {
	nxt[cnt] = head[u];
	to[cnt] = v;
	head[u] = cnt++;
}

}g,G;

int n,m,q,w[N];
int dfn[N],low[N],idx,ID;
int st[N],top;

multiset<int> s[N];

void tarjan(int x) {
	low[x] = dfn[x] = ++idx;
	st[++top] = x;
	for(int i = g.head[x];~i;i = g.nxt[i]) {
		int y = g.to[i];
		if(!dfn[y]) {
			tarjan(y);
			low[x] = min(low[x],low[y]);
			if(dfn[x] <= low[y]) {
				ID++;
				int v;
				do{
					v = st[top--];
					G.add(v,ID);
					G.add(ID,v);
				}while(v ^ y);
				G.add(ID,x);
				G.add(x,ID);
			}
		}else low[x] = min(dfn[y],low[x]);
	}
}

int fa[N],dep[N],id[N],_w[N],siz[N],son[N],num,_top[N],_id[N];

void dfs1(int x,int f) {
	dep[x] = dep[f] + 1;
	siz[x] = 1;
	fa[x] = f;
	for(int i = G.head[x];~i;i = G.nxt[i]) {
		int y = G.to[i];
		if(y ^ f) {
			dfs1(y,x);
			siz[x] += siz[y];
			if(siz[son[x]] < siz[y]) son[x] = y;
		}
	}
}

void dfs2(int x,int topx) {
	_top[x] = topx;
	id[x] = ++num;
	_id[num] = x;
	if(!son[x]) return;
	dfs2(son[x],topx);
	for(int i = G.head[x];~i;i = G.nxt[i]) {
		int y = G.to[i];
		if(y ^ fa[x] && y ^ son[x]) 
			dfs2(y,y);
	}
}

namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)

int t[N<<2];

void push_up(int p) {t[p] = min(t[ls],t[rs]);}

void build(int p,int pl,int pr) {
	if(pl == pr) {
		t[p] = w[_id[pl]];
		return;
	}
	build(ls,pl,mid);
	build(rs,mid+1,pr);
	push_up(p);
}

void update(int p,int pl,int pr,int k,int d) {
	if(pl == pr) {
		t[p] = d;
		return;
	}
	if(k <= mid) update(ls,pl,mid,k,d);
	if(k > mid) update(rs,mid+1,pr,k,d);
	push_up(p);
}

int query(int p,int pl,int pr,int l,int r) {
	if(l <= pl && pr <= r) return t[p];
	int res = inf;
	if(l <= mid) res = min(res,query(ls,pl,mid,l,r));
	if(r > mid) res = min(res,query(rs,mid+1,pr,l,r));
	return res;
}
}

int query(int x,int y) {
	int res = inf;
	while(_top[x] != _top[y]) {
		if(dep[_top[x]] < dep[_top[y]]) swap(x,y);
		res = min(res,sgt::query(1,1,num,id[_top[x]],id[x]));
		x = fa[_top[x]];
	}
	if(dep[x] > dep[y]) swap(x,y);
	res = min(res,sgt::query(1,1,num,id[x],id[y]));
	if(x > n) res = min(res,sgt::query(1,1,num,id[fa[x]],id[fa[x]]));
	return res;
}

void update(int x,int d) {
	sgt::update(1,1,num,id[x],d);
	if(fa[x]) {
		s[fa[x]].erase(s[fa[x]].lower_bound(w[x]));
		s[fa[x]].emplace(d);
			if(w[fa[x]] != *s[fa[x]].begin()) 
				w[fa[x]] = *s[fa[x]].begin();	
			sgt::update(1,1,num,id[fa[x]],w[fa[x]]);
	}
	w[x] = d;
}


signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	
	cin>>n>>m>>q;
	ID = n;
	for(int i = 1;i<=n;i++) {
		cin>>w[i];
		s[i].emplace(w[i]);
	}
	for(int i = 1;i<=m;i++) {
		int u,v;
		cin>>u>>v;
		g.add(u,v);g.add(v,u);
	}
	
	tarjan(1);
	dfs1(1,0);
	dfs2(1,1);
	for(int i = 1;i<=n;i++) 
		if(fa[i])
			s[fa[i]].emplace(w[i]);
	for(int i = n + 1;i<=ID;i++) 
	 	w[i] = *s[i].begin();
	
	sgt::build(1,1,num);

	while(q--) {
		char opt;int a,b;
		cin>> opt >> a >> b;
		switch(opt) {
		case 'C':
			update(a,b);
			break;
		case 'A': 
			cout<<query(a,b)<<'\n';
			break;
		}
	}


	return 0;
}

2024/07/28

P3792 由乃与大母神原型和偶像崇拜

因为题面太长就不放了 ~~真有你的 lxl~~

假做法：维护立方和，平方和，和，最大值，最小值，然后逐一判断

因为没有用 $ha s h$ 和自然溢出，用了 $KaTeX parse error: Expected group after '_' at position 1: _̲_int128$ 导致卡了会常

AC-code:

#include<bits/stdc++.h>
using namespace std;

#define int __int128

struct FastIO
{
#define get( ) getchar( )
#define put(x) putchar(x)
public:
	inline FastIO &operator >>(char &t)  { t = get(); return *this; }
	inline FastIO &operator >>(char *t)  { while((*t = get()) != '\n') *(++t) = '\0'; return *this; }
	template <typename type>
	inline FastIO &operator >>(type &x)  { x = 0; register int sig = 1; register char ch = get();
		while (ch < 48 || ch > 57) { if (ch == '-') sig = -1; ch = get(); }
		while (ch > 47 && ch < 58) x = (x << 3) + (x << 1) + (ch ^ 48),
		ch = get(); x *= sig; return *this; }
	template <typename type>
	inline FastIO &operator <<(type  x)  { if (!x) put('0'); if (x < 0) put('-'), x = -x; static char vec[50];
		register int len = 0; while (x) vec[len++] = x % 10 + '0', x /= 10;
		while (len--) put(vec[len]); return *this; }
	template <typename type>
	inline FastIO &operator <<(type *t)  { for (; *t; t++) put(*t); return *this; }
	inline FastIO &operator <<(char  t)  { put(t); return *this; }
}IO;

const int N = 500005,inf = 1e18;

int n,m,a[N];

#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)

int s[N<<2],s2[N<<2],s3[N<<2],mx[N<<2],mn[N<<2];

inline void push_up(int p) {
    s[p] = s[ls] + s[rs];
    s2[p] = s2[ls] + s2[rs];
    s3[p] = s3[ls] + s3[rs];
    mx[p] = max(mx[ls],mx[rs]);
    mn[p] = min(mn[ls],mn[rs]);
}

inline void build(int p,int pl,int pr) {
    if(pl == pr) {
        mn[p] = mx[p] = s[p] = a[pl];
        s2[p] = a[pl] * a[pl];
        s3[p] = a[pl] * a[pl] * a[pl];
        return;
    }
    build(ls,pl,mid);
    build(rs,mid+1,pr);
    push_up(p);
}

inline void update(int p,int pl,int pr,int k,int d) {
    if(pl == pr) {
        mn[p] = mx[p] = s[p] = d;
        s2[p] = d * d;
        s3[p] = d * d * d;
        return;
    }
    if(k <= mid) update(ls,pl,mid,k,d);
    else update(rs,mid+1,pr,k,d);
    push_up(p);
}

inline array<int,3> query(int p,int pl,int pr,int l,int r) {
    if(l <= pl && pr <= r) return array<int,3>{s[p],s2[p],s3[p]};
    if(r <= mid) return query(ls,pl,mid,l,r);
    else if(l > mid) return query(rs,mid+1,pr,l,r); 
    else  {
        array<int,3> a = query(ls,pl,mid,l,r),b = query(rs,mid+1,pr,l,r);
        array<int,3> c = array<int,3>{a[0] + b[0],a[1] + b[1],a[2] + b[2]};
        return c;
    }
}

inline int query_min(int p,int pl,int pr,int l,int r) {
    if(l <= pl && pr <= r) return mn[p];
    int res = inf;
    if(l <= mid) res = min(res,query_min(ls,pl,mid,l,r));
    if(r > mid) res = min(res,query_min(rs,mid+1,pr,l,r));
    return res;
}

inline int query_max(int p,int pl,int pr,int l,int r) {
    if(l <= pl && pr <= r) return mx[p];
    int res = -inf;
    if(l <= mid) res = max(res,query_max(ls,pl,mid,l,r));
    if(r > mid) res = max(res,query_max(rs,mid+1,pr,l,r));
    return res;
}

signed main() {

    IO>>n>>m;
    for(int i = 1;i<=n;i++) 
    	IO>>a[i];
    build(1,1,n);
    array<int,3> A;
	int opt,x,y,l,r;
	bool flag;
    while(m--) {
        IO>>opt>>x>>y;
        if(opt == 1) update(1,1,n,x,y);
        else {
            A = query(1,1,n,x,y);
            l = query_min(1,1,n,x,y),r = query_max(1,1,n,x,y);
            flag = true;
            if(A[0] != (r + 1) * r / 2 - (l - 1) * l / 2) flag = false;
            if(A[1] != r * (r + 1) * (2 * r + 1) / 6 - (l - 1) * l * (2 * l - 1) / 6) flag = false;
            if(A[2] != ((r + 1) * r / 2) * ((r + 1) * r / 2) - ((l - 1) * l / 2) * ((l - 1) * l / 2)) flag = false;
            if(flag) puts("damushen");
            else puts("yuanxing");
		}
    }
	return 0;
}

因为最近在归纳动态DP的模板，所以献上典题

P5024 [NOIP2018 提高组] 保卫王国

题面：

题目背景

NOIP2018 提高组 D2T3

题目描述

Z 国有 $n$ 座城市， $(n - 1)$ 条双向道路，每条双向道路连接两座城市，且任意两座城市都能通过若干条道路相互到达。

Z 国的国防部长小 Z 要在城市中驻扎军队。驻扎军队需要满足如下几个条件：

一座城市可以驻扎一支军队，也可以不驻扎军队。
由道路直接连接的两座城市中至少要有一座城市驻扎军队。
在城市里驻扎军队会产生花费，在编号为 $i$ 的城市中驻扎军队的花费是 $p_i$ 。

小 Z 很快就规划出了一种驻扎军队的方案，使总花费最小。但是国王又给小 Z 提出了 $m$ 个要求，每个要求规定了其中两座城市是否驻扎军队。小 Z 需要针对每个要求逐一给出回答。具体而言，如果国王提出的第 $j$ 个要求能够满足上述驻扎条件（不需要考虑第 $j$ 个要求之外的其它要求），则需要给出在此要求前提下驻扎军队的最小开销。如果国王提出的第 $j$ 个要求无法满足，则需要输出 $- 1$ 。现在请你来帮助小 Z。

输入格式

第一行有两个整数和一个字符串，依次表示城市数 $n$ ，要求数 $m$ 和数据类型 $t y p e$ 。 $t y p e$ 是一个由大写字母 A，B 或 C 和一个数字 1，2，3 组成的字符串。它可以帮助你获得部分分。你可能不需要用到这个参数。这个参数的含义在【数据规模与约定】中有具体的描述。

第二行有 $n$ 个整数，第 $i$ 个整数表示编号 $i$ 的城市中驻扎军队的花费 $p_i$ 。

接下来 $(n - 1)$ 行，每行两个整数 $u, v$ ，表示有一条 $u$ 到 $v$ 的双向道路。

接下来 $m$ 行，每行四个整数 $a, x, b, y$ ，表示一个要求是在城市 $a$ 驻扎 $x$ 支军队，在城市 $b$ 驻扎 $y$ 支军队。其中， $x, y$ 的取值只有 $0$ 或 $1$ ：

若 $x$ 为 $0$ ，表示城市 $a$ 不得驻扎军队。
若 $x$ 为 $1$ ，表示城市 $a$ 必须驻扎军队。
若 $y$ 为 $0$ ，表示城市 $b$ 不得驻扎军队。
若 $y$ 为 $1$ ，表示城市 $b$ 必须驻扎军队。

输入文件中每一行相邻的两个数据之间均用一个空格分隔。

输出格式

输出共 $m$ 行，每行包含一个个整数，第 $j$ 行表示在满足国王第 $j$ 个要求时的最小开销，如果无法满足国王的第 $j$ 个要求，则该行输出 $- 1$ 。

样例 #1

样例输入 #1
5 3 C3 
2 4 1 3 9 
1 5 
5 2 
5 3 
3 4 
1 0 3 0 
2 1 3 1 
1 0 5 0
样例输出 #1
12 
7 
-1
提示

样例 1 解释

对于第一个要求，在 $4$ 号和 $5$ 号城市驻扎军队时开销最小。
对于第二个要求，在 $1$ 号、 $2$ 号、 $3$ 号城市驻扎军队时开销最小。
第三个要求是无法满足的，因为在 $1$ 号、 $5$ 号城市都不驻扎军队就意味着由道路直接连接的两座城市中都没有驻扎军队。

数据规模与约定

测试点编号 $\text{type}$ $n = m =$
$1, 2$ A3 $10$
$3, 4$ C3 $10$
$5, 6$ A3 $100$
$7$ C3 $100$
$8, 9$ A3 $2\times 10^3$
$10, 11$ C3 $2\times 10^3$
$12, 13$ A1 $10^5$
$14, 15, 16$ A2 $10^5$
$17$ A3 $10^5$
$18, 19$ B1 $10^5$
$20, 21$ C1 $10^5$
$22$ C2 $10^5$
$23, 24, 25$ C3 $10^5$

数据类型的含义：

A：城市 $i$ 与城市 $i + 1$ 直接相连。
B：任意城市与城市 $1$ 的距离不超过 $100$ （距离定义为最短路径上边的数量），即如果这棵树以 $1$ 号城市为根，深度不超过 $100$ 。
C：在树的形态上无特殊约束。
1：询问时保证 $a = 1, x = 1$ ，即要求在城市 $1$ 驻军。对 $b, y$ 没有限制。
2：询问时保证 $a, b$ 是相邻的（由一条道路直接连通）
3：在询问上无特殊约束。

对于 $100\%$ 的数据，保证 $\leq n,m ≤ 10^5$ ， $1 ≤ p_i ≤ 10^5$ ， $\leq u, v, a, b \leq n$ ， $\neq b$ ， $\in \{0, 1\}$ 。

测试点编号	$\text{type}$	$n = m =$
$1, 2$	`A3`	$10$
$3, 4$	`C3`	$10$
$5, 6$	`A3`	$100$
$7$	`C3`	$100$
$8, 9$	`A3`	$2\times 10^3$
$10, 11$	`C3`	$2\times 10^3$
$12, 13$	`A1`	$10^5$
$14, 15, 16$	`A2`	$10^5$
$17$	`A3`	$10^5$
$18, 19$	`B1`	$10^5$
$20, 21$	`C1`	$10^5$
$22$	`C2`	$10^5$
$23, 24, 25$	`C3`	$10^5$

AC-code:

#include <bits/stdc++.h>
using namespace std;

namespace my{
using namespace AllRangeApply_Define;
using namespace Atomic::normalSTD;
//using namespace Atomic::fastSTD;
//using namespace Atomic::SuperSTD;

CIN N = 1e5+5,INF = 5e9;

struct Edge{
	int nxt,to;
}edge[N<<1];
int head[N],cnt;

void init(){
	memset(head,-1,sizeof(head));
	for(int i = 0;i<(N<<1);i++) edge[i].nxt = -1;
	cnt = 0;
}

void addedge(int u,int v){
	edge[cnt].nxt = head[u];
	edge[cnt].to = v;
	head[u] = cnt++;
}

int F[N][2],w[N];

struct matrix{
	int m[2][2];
	matrix(){m[0][0] = m[1][0] = m[0][1] = m[1][1] = INF;}
	int* operator [](const int pos) {return m[pos];}
	friend matrix operator *(matrix a,matrix b){
		matrix c;
		for(int i = 0;i<2;i++) 
			for(int j = 0;j<2;j++) 
				for(int k = 0;k<2;k++) 
					c[i][j] = min(c[i][j],a[i][k] + b[k][j]);
		return c;
	}
};

matrix k[N];
int ed[N],son[N],fa[N],size[N],dep[N],id[N],dfn[N],top[N];
int num;
int n,m;

void dfs1(int x,int f){
	fa[x] = f;
	size[x] = 1;
	dep[x] = dep[f] + 1;
	for(int i = head[x];~i;i = edge[i].nxt){
		int y = edge[i].to;
		if(y ^ f) {
			dfs1(y,x);
			size[x] += size[y];
			if(size[son[x]] < size[y]) son[x] = y;
		}
	}
}

void dfs2(int x,int topx){
	id[x] = ++num;
	dfn[num] = x;
	top[x] = topx;

	ed[topx] = max(ed[topx],num);

	F[x][0] = 0;
	F[x][1] = w[x];
	k[x][0][1] = 0;
	k[x][1][0] = k[x][1][1] = w[x];
	if(!son[x]) return;
	dfs2(son[x],topx);
	F[x][0] += F[son[x]][1];
	F[x][1] += min(F[son[x]][1],F[son[x]][0]);
	for(int i = head[x];~i;i = edge[i].nxt){
		int y = edge[i].to;
		if(y ^ fa[x] && y ^ son[x]) {
			dfs2(y,y);
			F[x][0] += F[y][1];
			F[x][1] += min(F[y][0],F[y][1]);
			k[x][0][1] += F[y][1];
			k[x][1][0] += min(F[y][0],F[y][1]);
			k[x][1][1] = k[x][1][0];
		}
	}
}

namespace sgm{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)

matrix t[N<<2];

void push_up(int p){
	t[p] = t[ls] * t[rs];
}

void build(int p,int pl,int pr){
	if(pl == pr) {
		t[p] = k[dfn[pl]];
		return;
	}
	build(ls,pl,mid);
	build(rs,mid+1,pr);
	push_up(p);
}

void update(int p,int pl,int pr,int kk){
	if(pl == pr && pl == kk) {
		t[p] = k[dfn[pl]];
		return;
	}
	if(kk <= mid) update(ls,pl,mid,kk);
	else update(rs,mid+1,pr,kk);
	push_up(p);
}

matrix query(int p,int pl,int pr,int l,int r){
	if(l <= pl && pr <= r) return t[p];
	if(r <= mid) return query(ls,pl,mid,l,r);
	else if(l > mid) return query(rs,mid+1,pr,l,r);
	else return query(ls,pl,mid,l,r) * query(rs,mid+1,pr,l,r);
}

}

void update(int x,int opt,int d){
	if(!opt){
		k[x][1][0] += d * INF;
		k[x][1][1] = k[x][1][0];
	}else {
		k[x][0][1] += d * INF;	
	}
	

	matrix fir,sec;
	while(x != 0) {
		fir = sgm::query(1,1,n,id[top[x]],ed[top[x]]);
		sgm::update(1,1,n,id[x]);
		sec = sgm::query(1,1,n,id[top[x]],ed[top[x]]);
		x = fa[top[x]];

		k[x][1][0] += min(sec[0][1],sec[1][1]) - min(fir[0][1],fir[1][1]);
		k[x][1][1] = k[x][1][0];
		k[x][0][1] += sec[1][1] - fir[1][1];
	}
}

string opt;

signed main(){
	speed_up(true);
	init();

	cin>>n>>m;
	cin>>opt;
	for(int i = 1;i<=n;i++) cin>>w[i];
	for(int i = 1;i<n;i++) {
		int u,v;
		cin>>u>>v;
		addedge(u,v);
		addedge(v,u);
	}
	
	dfs1(1,0);
	dfs2(1,1);
	sgm::build(1,1,n);

	while(m--){
		int a,x,b,y;
		cin>>a>>x>>b>>y;
        if(!x && !y && (fa[b] == a || fa[a] == b)){
            cout<<-1<<'\n';
            continue;
        }
		update(a,x,1);
		update(b,y,1);
		matrix ans = sgm::query(1,1,n,id[1],ed[1]);
		int res = min(ans[1][1],ans[0][1]);
		cout<<res<<'\n';
		update(a,x,-1);
		update(b,y,-1);
	}
	return 0;
}

}
signed main() {
	return my::main();
}

2024/07/30

梦熊训练赛

D.Max and Mex

给定三个整数，和一棵个点的树。

树的每个点有点权，保证点权两两不同。

对于树的一条链，设其点权集合的为，点权集合的为，则这条链的价值为。

求出价值最大的链的价值。

注：集合的定义为最小的未在该集合中出现过的非负整数。

第一行三个整数。

第二行个整数表示。

接下来的行，每行两个整数表示一条树边。

一行一个整数表示答案。

输入样例1

输出样例1

输入样例2

20 1 1
10 18 13 8 19 15 0 14 11 17 12 5 4 9
16 2 1 6 7 3
17 9
6 17
20 17
4 17
18 9
15 17
2 18
13 2
3 20
12 15
10 18
5 3
11 20
7 13
16 12
1 12
8 15
19 11
14 7

输出样例2

保证两两不同。

$\max$ 太难控制了，但是 $m e x$ 很好控制，因为每个节点的权值互不相同

我们可以通过 $df s$ 枚举

然后在路径两端和路径上找 $\max$

AC-code(但没过CF，应该是扩展链没写对~~但我不想改辣~~):

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 1e5+5;
int n,c,d,a[N],ans;
int head[N],nxt[N<<1],to[N<<1],cnt;
void init() {memset(head,-1,sizeof(head));}
void add(int u,int v){
    nxt[cnt] = head[u];
    to[cnt] = v;
    head[u] = cnt++;
}
int fa[N],top[N],num,dep[N],siz[N],son[N],pos[N],id[N],w[N];
void dfs1(int x,int f) {
    fa[x] = f;
    dep[x] = dep[f] + 1;
    siz[x] = 1;
    for(int i = head[x];~i;i = nxt[i]) {
        int y = to[i];
        if(y ^ f) {
            dfs1(y,x);
            siz[x] += siz[y];
            if(siz[son[x]] < siz[y]) son[x] = y;
        }
    }
}
void dfs2(int x,int topx) {
    top[x] = topx;
    id[x] = ++num;
    w[num] = a[x];
    if(!son[x]) return;
    dfs2(son[x],topx);
    for(int i = head[x];~i;i = nxt[i]) {
        int y = to[i];
        if(y ^ fa[x] && y ^ son[x]) dfs2(y,y);
    }
}
int lca(int x,int y) {
    while(top[x] !=  top[y]) {
        if(dep[top[x]] < dep[top[y]]) swap(x,y);
        x = fa[top[x]];
    }
    if(dep[x] > dep[y]) swap(x,y);
    return x;
}

namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)

int mx[N<<2];

void push_up(int p) {mx[p] = max(mx[ls],mx[rs]);}

void build(int p,int pl,int pr) {
    if(pl == pr) {mx[p] = w[pl];return;}
    build(ls,pl,mid);
    build(rs,mid+1,pr);
    push_up(p);
}

int query(int p,int pl,int pr,int l,int r) {
    if(r < l) return 0;
    if(l <= pl && pr <= r) return mx[p];
    int res = 0;
    if(l <= mid) res = max(res,query(ls,pl,mid,l,r));
    if(r > mid) res = max(res,query(rs,mid+1,pr,l,r));
    return res;
}
}

int query(int x,int y) {
    if(id[x] > id[y]) return 0;
    int r = 0;
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]]) swap(x,y);
        r = max(r,sgt::query(1,1,num,id[top[x]],id[x]));
        x = fa[top[x]];
    }   
    if(dep[x] > dep[y]) swap(x,y);
    r = max(r,sgt::query(1,1,num,id[x],id[y]));
    return r;
}

int query(int x) {return sgt::query(1,1,num,id[x],id[x] + siz[x] - 1);}

void solve(int D,int x,int y){
	if(dep[x] > dep[y]) swap(x,y); 
    int LCA = lca(x,y);
    int r = query(x,y);
    if(LCA == x) {
        for(int i = head[x];~i;i = nxt[i]) {
            int v = to[i];
            if(fa[x] ^ v) 
                if(lca(y,v) == v){
                    r = max(r,max(sgt::query(1,1,num,1,id[v]-1),sgt::query(1,1,num,id[v] + siz[v],num)));
                    r = max(r,query(y));
                    ans = max(ans,c * (D + 1) + d * r);
                }
        }
    }else {
        r = max(query(x),r);
        r = max(query(y),r);
        ans = max(ans,c * (D + 1) + d * r);
    }
    int nxtPos = pos[D + 1];
    int lt = lca(x,nxtPos),rt = lca(y,nxtPos);
    if(lt == nxtPos || rt == nxtPos)
    	solve(D + 1,x,y);
    else if(lt == x && rt == y) 
    	solve(D + 1,x,nxtPos);
    else if(lt == x && rt != y) {
    	if(LCA == x)
    		for(int i = head[x];~i;i = nxt[i]) {
    			int v = to[i];
    			if(v ^ fa[x] && lca(v,y) == v && lca(nxtPos,v) == v)
    				return;
			}
    	solve(D + 1,nxtPos,y);
	} 	
}

signed main() {
    init();
    n = rd(),c = rd(),d = rd();
    for(int i = 1;i<=n;i++) a[i] = rd(),pos[a[i]] = i;
    for(int i = 1,u,v;i<n;i++) {
        u = rd(),v = rd();
        add(u,v);add(v,u);
    }
    dfs1(pos[0],0);
    dfs2(pos[0],pos[0]);
    sgt::build(1,1,num);
    int _max = 0;
    for(int i = 1;i<=n;i++) _max = max(_max,a[i]);
    ans = _max * d + c;
    solve(1,pos[0],pos[1]);
    wt(ans);
	return 0;
}

$7$ 月结束力，接下来是永无止境的八月！

MingJunYi

关注

16
点赞
踩
12

收藏

觉得还不错? 一键收藏
0
评论
2024.7 - 做题记录与方法总结 - Part 4

2024/07/23梦熊题单E.基础数据结构题题目描述给定一个长度为 n 的序列 A ，下标从 1 开始，你需要维护三种操作：1{\kern 4pt}l{\kern 4pt}r{\kern 4pt}x: 对于 l \leq i \leq r ，令 A_i=A_i+x 。2{\kern 4pt}l{\kern 4pt}r: 对于 l \leq i \leq r ，令 A_i=\lfloor \sqrt{A_i} \rfloor 。3{\kern 4pt}l{
复制链接

扫一扫