BSC 信道容量公式推导

---

1. 信道容量定义

信道容量 $C$ 是输入和输出之间互信息 $I(X;Y)$ 的最大值：
$$C=\underset{P(X)}{\max }I(X;Y)$$
互信息 $I(X;Y)$ 的公式为：
$$I(X;Y)=H(Y)-H(Y|X)$$
其中：

• $H(Y)$ 是输出符号 $Y$ 的熵，表示接收端的总信息量。
• $H(Y|X)$ 是条件熵，表示信道的不确定性。

对于 二进制对称信道（BSC）：

• 输入 $X$ 是 { 0 , 1 } \{0, 1\} {0,1}。
• $P(X=0)=p_0,P(X=1)=p_1$，且 $p_1=1-p_0$。
• 信道翻转比特的概率为 $p$ （即 $P(Y\ne X)=p$）。

---

2. 条件概率

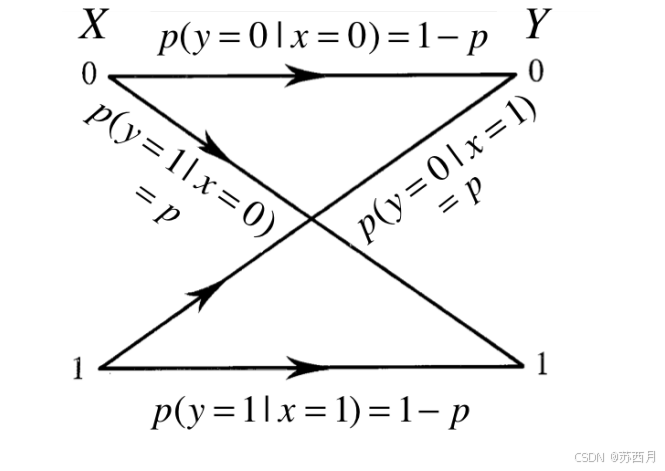
BSC 的条件概率定义如下：
$$P(Y=0|X=0)=1-p,P(Y=1|X=0)=p$$
$$P(Y=1|X=1)=1-p,P(Y=0|X=1)=p$$

---

3. 联合概率

联合概率 $P(X,Y)$ 表示输入 $X$ 和输出 $Y$ 的联合分布：
$$P(X=0,Y=0)=P(Y=0|X=0)\cdot P(X=0)=p_0(1-p)$$
$$P(X=1,Y=1)=P(Y=1|X=1)\cdot P(X=1)=p_1(1-p)$$
$$P(X=0,Y=1)=P(Y=1|X=0)\cdot P(X=0)=p_{0}p$$
$$P(X=1,Y=0)=P(Y=0|X=1)\cdot P(X=1)=p_{1}p$$

---

4. 边缘概率

边缘概率 $P(Y)$ 表示输出 $Y$ 的分布：
$$P(Y=0)=P(X=0,Y=0)+P(X=1,Y=0)$$
$$P(Y=0)=p_0(1-p)+p_{1}p$$
$$P(Y=1)=P(X=0,Y=1)+P(X=1,Y=1)$$
$$P(Y=1)=p_{0}p+p_1(1-p)$$

---

5. 互信息的展开

互信息 $I(X;Y)$ 的公式可以写为：
I ( X ; Y ) = ∑ x ∈ { 0 , 1 } ∑ y ∈ { 0 , 1 } P ( X = x , Y = y ) log ⁡ 2 P ( X = x , Y = y ) P ( X = x ) P ( Y = y ) I(X; Y) = \sum_{x \in \{0, 1\}} \sum_{y \in \{0, 1\}} P(X = x, Y = y) \log_2 \frac{P(X = x, Y = y)}{P(X = x) P(Y = y)} I(X;Y)=x∈{0,1}∑​y∈{0,1}∑​P(X=x,Y=y)log2​P(X=x)P(Y=y)P(X=x,Y=y)​

将联合概率和边缘概率代入公式：
I ( X ; Y ) = ∑ x ∈ { 0 , 1 } ∑ y ∈ { 0 , 1 } P ( X = x , Y = y ) log ⁡ 2 P ( Y = y ∣ X = x ) P ( Y = y ) I(X; Y) = \sum_{x \in \{0, 1\}} \sum_{y \in \{0, 1\}} P(X = x, Y = y) \log_2 \frac{P(Y = y | X = x)}{P(Y = y)} I(X;Y)=x∈{0,1}∑​y∈{0,1}∑​P(X=x,Y=y)log2​P(Y=y)P(Y=y∣X=x)​

---

6. 化简互信息公式

对互信息公式进行化简，结合前述概率关系，可得：
I ( X ; Y ) = ∑ x ∈ { 0 , 1 } P ( X = x ) ∑ y ∈ { 0 , 1 } P ( Y = y ∣ X = x ) log ⁡ 2 P ( Y = y ∣ X = x ) P ( Y = y ) I(X; Y) = \sum_{x \in \{0, 1\}} P(X = x) \sum_{y \in \{0, 1\}} P(Y = y | X = x) \log_2 \frac{P(Y = y | X = x)}{P(Y = y)} I(X;Y)=x∈{0,1}∑​P(X=x)y∈{0,1}∑​P(Y=y∣X=x)log2​P(Y=y)P(Y=y∣X=x)​

具体展开：
$$I(X;Y)=p_0\left[(1-p){\log }_2\frac{1-p}{P(Y=0)}+p{\log }_2\frac{p}{P(Y=1)}\right]+p_1\left[p{\log }_2\frac{p}{P(Y=0)}+(1-p){\log }_2\frac{1-p}{P(Y=1)}\right]$$

---

7. 最大化互信息

信道容量 $C$ 是互信息的最大值：
$$C=\underset{p_0}{\max }I(X;Y)$$

代入边缘概率 $P(Y)$ 和条件熵的关系，经过化简可以得到：
$$C=\underset{p_0}{\max }[H(Z)-H(p)]$$
其中：

• $H(p)=-p{\log }_{2}p-(1-p){\log }_2(1-p)$，为熵函数。
• $Z=p_0(1-p)+p_{1}p$。

---

8. 结论：最大容量

为了最大化 $C$，令输入分布均匀，即 $p_0=p_1=0.5$。此时：
$$Z=0.5\cdot (1-p)+0.5\cdot p=0.5$$
$$H(Z)=H(0.5)=1$$

因此，信道容量为：
$$C=1-H(p)$$
即：
$$C=1+p{\log }_{2}p+(1-p){\log }_2(1-p)$$

---

总结

BSC 的信道容量 $C=1-H(p)$ 是通过最大化输入输出的互信息得到的。它表明：

• 当翻转概率 $p=0$（无噪声）时，$C=1$ 比特/符号。
• 当翻转概率 $p=0.5$（完全随机）时，$C=0$ 比特/符号。