重构大学数学基础_week03_欧拉公式的几何理解

在漫漫数学银河中，诞生了无数美丽的数学公式，他们宛如一颗颗璀璨的明珠光彩夺目，而只有一个公式被称为上帝公式，它就是欧拉公式。欧拉公式对我们来说都不陌生，但是如何从几何角度理解这个公式呢？我们来看一下它有什么特别之处。

它的形式是这样的：

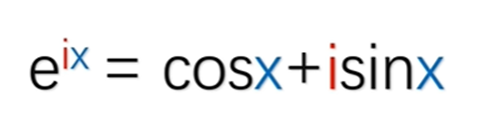
其中e是自然常数，i是虚数，sincos是三角函数。当X等于π的时候，公式就变成了

这个公式就是欧拉恒等式，这个等式包含了自然常数，虚数，圆周率和自然数。每一个单拎出来都是数学领域中非常重要的存在。而欧拉公式将这些数以一种简洁的形式结合在一起。

我先解释一下欧拉公式的几何意义。

复指数函数在复平面上的表现形式与单位圆紧密相关，这一性质是基于欧拉

公式将复数的指数形式与三角函数联系起来。当我们考虑 𝑥为实数时，的实部是cos(x)，虚部是sin(x)。

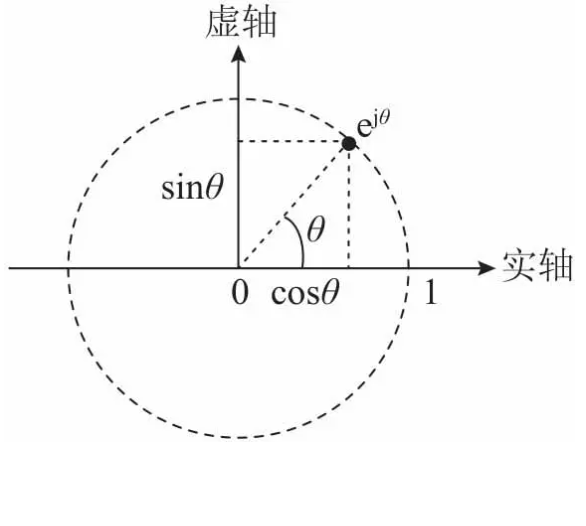
在复平面上，以实数x为横坐标，虚数i为纵坐标，一个点可以用坐标(a,b) 来表示，其中 a 是实部，b是虚部，这对应于复数。当考虑时，随着 𝑥从 0变化到 2𝜋，点 (cos(x),sin(x)) 在单位圆上描绘出一条路径，这是因为：

cos(x) 表示该点沿水平（实轴）方向的位置，其值范围从 -1 到 1。

sin(x) 表示该点沿垂直（虚轴）方向的位置，其值范围同样从 -1 到 1。

随着 𝑥增加：

• 当 x=0， cos(0)=1， sin(0)=0，点位于单位圆的正实轴上（即点 (1, 0)）。
• 随着 𝑥 从 0增加到 𝜋，点沿单位圆逆时针移动到点 (−1,0)。
• 当 x=π， cos(π)=−1， sin(π)=0。
• 继续增加 𝑥 直到2π，点又回到了起点 (1,0)。

因此，描述了单位圆上的一点随角度 𝑥 的变化而逆时针旋转的路径。这个旋转的速度是均匀的，每增加 2𝜋，点就完成一圈完整的旋转，这正好对应于复数的周期性。这就是为什么复指数函数 在复平面上可以表示为逆时针旋转的单位圆的原因。

那么，对求导的几何意义是什么呢？

已知欧拉公式为:

 

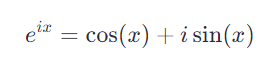
对两边同时求导，得到:

使用三角恒等变换

可以重写上述结果为:

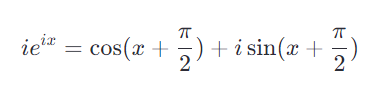
这表明的导数等于原函数乘以𝑖，在复平面上这相当于将原点处的向量逆时针旋转了 90∘或 𝜋/2​ 弧度。这是因为乘以 𝑖实际上是在做以下变换：

• 实部变为原来的虚部，
• 虚部变为原来实部的相反数，

这样的操作效果就是在复平面上将向量旋转了 90∘，保持模长不变。因此，复指数函数的导数不仅在数学上表现为乘以 𝑖，在几何上也直观地对应于复平面上的逆时针旋转 90∘。

求导得到的式子在物理运动上有什么含义呢？

我们回头看一下之前求导的结果，我们将原函数当作位置函数，那么求导后就是速度函数，而我们可以发现，速度的方向就是位置的九十度旋转，这就解释了为什么会绕着单位圆旋转。

那么欧拉公式的应用有哪些呢？

欧拉公式将三角函数与复指数函数联系起来，提供了一种强大的复数表示方法。在信号分析中，傅里叶变换是将时域信号转换为频域信号的关键手段，而时域信号常常涉及正弦波和余弦波的组合。通过欧拉公式，这些正弦余弦波可以被复指数函数替代，其中 𝜔 是角频率，𝑡是时间。傅里叶变换中，信号被分解为不同频率的正弦波分量的线性组合。由于欧拉公式允许将三角函数转换为指数形式，这极大地简化了傅里叶变换的计算过程。使用复指数函数作为基函数，可以将原本涉及多个三角函数的积分简化为单一的复数运算，使得分析更加直观和高效。

麦克斯韦方程组的解经常涉及到复数表示，尤其是在求解波动问题时。电磁波的传播可以用复指数函数来描述，这里 𝑘是波数，𝜔是角频率，𝑧和 𝑡分别代表空间和时间变量。这个复指数形式可以直接从欧拉公式推导出来，帮助我们更容易地处理波动的振幅和相位信息。

在计算机图形学中，旋转是基本的几何变换之一。虽然通常使用矩阵来表示3D空间中的旋转，但旋转操作的本质可以追溯到复数平面上的旋转，即通过复数乘法实现。复数表示逆时针旋转 θ 弧度，这启发了如何在计算机中高效地实现二维图形的旋转。例如，当处理纹理映射、图标旋转或任何涉及2D图形的旋转时，欧拉公式的思想简化了算法的设计。