人工智能数学基础——高等数学

1.方向导数

对于，有：

如果函数的增量，与这两点距离的比例存在，则称此为在P点沿着L的方向导数,

函数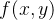： 在X轴正向  ，Y轴正向 的方向导数 分别为： 负方向导数

 定理：

定理：如果函数 在点 是可微分的，那么在该点 沿任意方向L的方向导数都存在

 为X轴到L的角度

示例：

 2.梯度

        梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。 

        函数在某点的梯度是一个向量，它的方向与方向导数最大值取得的方向一致。 其模大小正好是最大的方向导数

 

 示例：

3.泰勒公式

        出发点： 

        用简单的熟悉的多项式来近似代替复杂的函数

        易计算函数值，导数与积分仍是多项式 

        多项式由它的系数完全确定，其系数又由它在一点的函数值及其导数所确定。

        

        微分：

         以直代曲

 

 注意：当x逐渐偏离0，差距越来越大

但是，只用一阶导数显然是不准确的

 一阶导数只帮我们定位了下一个点是上升还是下降对之后的趋势就很难把控了

如果说将二阶导数用上，显然会更加准确 

 

因此，用的导数阶数越多，准确度越高 

泰勒多项式

称为 的在x0关于（x-x0）的n阶泰勒多项式

麦克劳林公式

 

近似可得： 

 阶乘的意义

        对于一个复杂函数，给我们的感觉时在当前点，低阶 项能更好的描述当前点附近，对于之后的走势就越来越依靠高阶的了

        如果把9次的和2次的直接放在一起，那2次的就不用玩了。 但是在开始的时候应该是2次的效果更好，之后才是慢慢轮到9次的呀！

 

有了阶乘之后，就帮助我们解决了这样的问题。 

多项式逼近，逼近sinx

 

4.拉格朗日乘子法

           对于函数Z=f(x,y),我们可以通过求偏导求得极值点，现在问题难度加大了，如果再加上约束条件呢？ 面积固定，求体积最大：

        山峰的高度是f(x,y) ，其中有一条曲线是 g(x,y)=c, 曲线镶嵌在山上，如何找到曲线最低点呢？因此，我们可以画两条直线，一条为过该点的直线，一条为该点的切线，根据函数的最值必定为函数的极值可以知道，当两条直线重合时，该点可取得最值，因此，两直线的法线平行。

 

求解

 

 自变量多于两个条件下

实例：