本博文是基于何子述《信号与系统》和奥本海姆《信号与系统》第二版编写,主要是为了记录自己的学习过程
1. 信号的概念
1.1 信号的定义
1.2 因果、逆因果信号的概念
1.2.1 因果信号
因果信号一定是右边信号,但右边信号不一定是因果信号
1.2.2 逆因果信号
逆因果信号一定是左边信号,但左边信号不一定是逆因果信号
1.2.3 时限信号
1.2.4 右边信号
1.2.5 左边信号
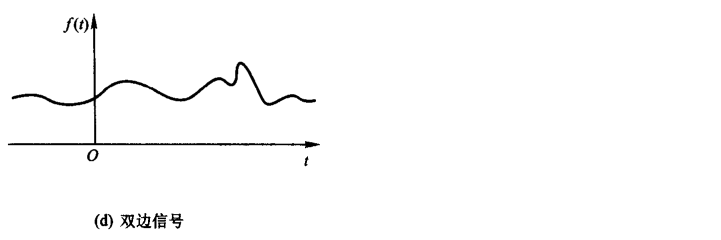
1.2.6 双边信号
2. 信号的分类
2.1 确定信号与随机信号
2.2 连续时间信号与离散时间信号
工程上,经常将连续时间信号称为模拟信号。
如果将离散时间信号的信号值用有限位数的二进制数表示,那这样的离散时间信号。
2.3 实信号与复信号
说明:复信号本身是不存在的,它存在的意义是为了在某些信号处理中描述问题的方便
2.4 指数信号与正弦信号
2.4.1 连续时间复指数信号与正弦信号
2.4.1.1 实指数信号
2.4.1.2 周期复指数和正弦信号
2.4.1.3 一般复指数信号
2.4.2 离散时间复指数信号与正弦信号
与连续时间复指数信号与正弦信号基本相同,这里不做赘述。
2.5 周期信号与非周期信号
2.5.1 周期信号与非周期信号的定义
2.5.2 周期信号与非周期信号的判断
首先可以根据图像判断:
①信号在时间轴两端必须是无限的 ②信号的形状上的每一点都务必周期性的重现
连续信号周期非周期判断:
对于单个正弦信号,只要周期T=2π/w存在(不需要为有理数)即为周期信号,否则为非周期信号。
对于两个正弦信号相加,无论T1、T2是否为有理数,只需要T1/T2为有理数即为周期信号,其中周期T为T1和T2的最小公倍数,否则为非周期信号。
离散信号周期非周期判断:
对于单个正弦序列,只要N=2π/Ω为有理数时即为周期信号,否则为非周期信号,其中周期N必须要为整数。
对于两个正弦序列相加,只要其中一个为非周期信号则相加后也为非周期信号,若两个都为周期信号,那么相加一定为周期信号,周期N为N1和N2的最小公倍数。
几个结论:
①连续周期信号之和不一定为周期信号
②离散周期信号之和一定为周期信号
③非周期信号作为线性时不变系统的输入,输出不一定为非周期信号
④周期信号作为线性时不变系统的输入,输出一定为周期信号,周期T保持
2.6 能量信号与功率信号
能量、功率信号的判断:
一般地,周期信号都为功率信号,其平均功率可以在一个周期内计算得到。 非周期信号分三种讨论:
①在有限时间内有一定幅值,但当t->±∞时幅值为0的信号为能量信号。这类信号也可以称为脉冲信号。
②当t->±∞时幅值不为无穷大,并且至少有一边为有限值的信号为功率信号。
③当t->±∞时只要有一边幅值为无穷大的信号为非能量非功率信号。
因此得出几个结论:
①时限信号为能量信号
②周期信号为功率信号
③非周期信号可能为能量信号也可能为功率信号
④有非能量非功率信号
⑤总能量有限的信号,平均功率必为0
⑥平均功率有限的信号,总功率必为无穷大
⑦平均功率和总能量均不为有限的信号理论上不存在
2.7 偶信号与奇信号
3. 信号的自变量变换
3.1 信号的时移
f(t) -> f(t ± t0):左加右减
3.2 信号的时间尺度变换
f(t) -> f(at):0<a<1时信号展宽到原来的1/a;a>1时信号压缩到原来的1/a
说明:对于离散信号的尺度变换与连续信号不太相同。
例如:
f[n] -> f1[n] = f[(1/2)n]
原来信号n=……0、1、2、3……的信号幅值变为n=……0、2、4、6……的信号幅值,并且原来信号n=……1、3、5……处信号幅值变为0并未消失,此时可从信号f1[n]恢复出信号f[n]。
例如:
f[n] -> f2[n] = f[2n]
原来信号n=……0、2、4……的信号幅值变为n=……0、1、2……的信号幅值,并且原来信号n=……1、3、5……处信号幅值消失,此时不能从信号f2[n]恢复出信号f[n]。
3.3 信号的时间反转
f(t) -> f(-t):将f(t)关于y轴对称折叠的图像即为f(-t)
3.4 先时移再尺度变换最后时间反转
若目标信号是原信号经过时移、尺度和反转变化的,建议先时移再尺度最后反转;
而对于要将已经经过时移、尺度和反转的信号变换为原信号f(t),建议先反转再尺度最后时移。例如:
f(t) -> f(-(1/2)t - 1) 先时移变为f(t-1),再尺度变为f((1/2)t -
1),最后反转变为f(-(1/2)t - 1)即为目标信号。再按逆序即可变为原信号f(t)。
说明:自变量变换只是对t变换,不是对括号内整体变换
例如:
f(2t-1)反转变为f(-2t-1),不是f(1-2t)
f(2t)右移2之后是f(2(t-2)) = f(2t-4),不是f(2t-2)
f(t-2)压缩2倍后是f(2t-2),不是f(2(t-2))
4. 信号的基本运算
4.1 两信号相加
两信号对应时刻的信号(函数)值相加,得到一个新信号
4.2 两信号相乘
两信号对应时刻的信号(函数)值相乘,得到一个新信号
4.3 连续时间信号的导数与积分
求导即对信号f(t)关于时间变量t求导:
同样地,积分即对信号f(t)关于时间变量t积分:
求导和积分可以统一表示为:
因此:
4.4 离散时间信号的差分和累加
差分的定义为:
二阶差分为:
累加的定义为:
与积分运算类似,可定义离散时间信号f[n]的m次累加:
先累加再差分:
4.5 信号的奇偶分解
利用信号的奇部和偶部可以为计算一个信号的相关运算提供一个思路
5. 单位冲激信号和单位阶跃信号
5.1 离散时间单位冲激信号和单位阶跃信号
5.1.1 离散时间单位冲激信号
该信号满足:
5.1.2 离散时间单位阶跃信号
5.1.3 二者的关系
因此,二者是互为差分累加的关系
5.2 连续时间单位冲激信号和单位阶跃信号
5.2.1 连续时间单位冲激信号
可以看到该方波面积始终为1
当方波宽度趋于0时,则为单位冲击信号:
图中箭头表示信号在t=0时幅度趋于无穷大由于其面积始终为1,故:
5.2.2 连续时间单位阶跃信号
5.2.3 二者的关系
5.3 单位冲激信号的性质
6. 系统的概念
6.1 系统的定义
6.2 系统的相互连接
系统并联:
系统串联:
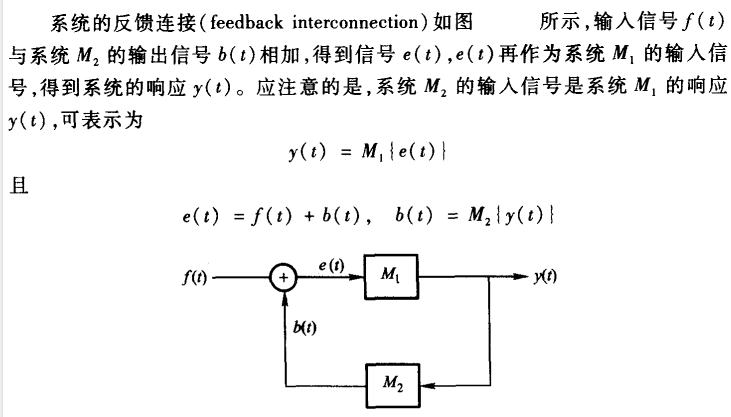
系统反馈:
7. 系统的性质
7.1 记忆性
一般的,若冲激信号作为输入信号,则该系统为非记忆系统。
7.2 因果性
通俗地讲,就是先有输入才能有输出,即先有输入信号作用到系统中才能有输出信号输出。
7.3 可逆性
例如:y=x ^ 2不可逆,因为x=±1时,y都为1。其逆函数为y=x ^ (1/2),定义域为x>=0,再将逆函数取逆显然不可还原出原函数,只能还原出原函数的一半。
7.4 稳定性
信号与系统中判断稳定的方法有四种:
①有界的输入信号产生有界的输出信号系统则稳定
②单位冲激响应绝对可积的系统则稳定
③S域包含收敛于包含虚轴的系统则稳定
④Z域收敛域包含单位圆的系统则稳定
7.5 时不变性
简单来说就是x(t-t0) -> y(t-t0)
7.6 线性
说明:y(t) = af(t) + b是非线性的,因为该系统不满足叠加定理。








 本文详细介绍了信号的概念,包括信号的定义、分类如确定与随机信号、连续与离散时间信号、实与复信号等。还探讨了指数和正弦信号、周期与非周期信号的特性,以及能量和功率信号的区别。此外,讲解了信号的自变量变换、基本运算,以及单位冲激和单位阶跃信号的性质。文章最后提到了系统的概念和一些关键性质,如线性时不变系统。
本文详细介绍了信号的概念,包括信号的定义、分类如确定与随机信号、连续与离散时间信号、实与复信号等。还探讨了指数和正弦信号、周期与非周期信号的特性,以及能量和功率信号的区别。此外,讲解了信号的自变量变换、基本运算,以及单位冲激和单位阶跃信号的性质。文章最后提到了系统的概念和一些关键性质,如线性时不变系统。

































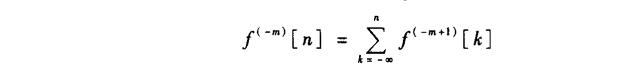








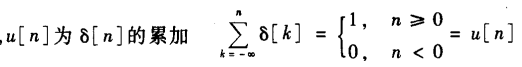


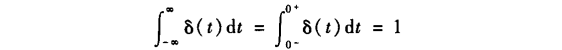






































 737
737

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








