快速排斥实验
假设以线段P1,P2为对角线作一矩形R,再以Q1,Q2为对角线作矩形T,当两个矩形不相交的时候两条线段肯定不相交,即线段相交的必要条件时矩形相交。

P1坐标为(p1x,p1y),P2坐标为(p2x,p2y),Q1的坐标为(q1x,q1y),Q2的坐标为(q2x,q2y)。
那矩形相交的条件就是:
min(p1x,p2x) <= max(q1x,q2x) &&
min(q1x,q2x) <= max(p1x,p2x) &&
min(p1y,p2y) <= max(q1y,q2y) &&
min(q1y,q2y) <= max(p1y,p2y);
跨立实验
两个坐标A(x1,y1),B(x2,y2),那么AxB的向量积就是x1y2-y1x2。
我们假定一个向量积R,R=x1y2-y1x2。
R<0 说明A在B的逆时针方向
R=0 说明A与B共线,可能正向也可能反向
R>0 说明A在B的顺时针方向
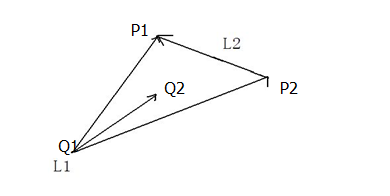
如果一条线段P1P2跨过了线段Q1Q2,那么P1,P2就分布在线段Q1Q2的两边,那么
((P1-Q1)×(Q2-Q1))*((Q2-Q1)×(P2-Q1))>0 【此为条件1】。
注意“ × ”是叉乘的意思,而“ * ”才是点乘。
(P1-Q1)×(Q2-Q1)能得出线段Q1P1跟线段Q1Q2叉乘结果的向量的方向,(Q2-Q1)×(P2-Q1)同样也会得出线段Q1Q2和线段Q1P2叉乘结果的向量的方向,只有这两个结果向量的点乘结果大于0,即这两个结果向量的方向一致时,P1,P2才会分布在线段Q1Q2的两边。
同理Q1Q2分布在P1P2两边的条件为
((Q1-P1)×(P2-P1))*((P2-P1)×(Q2-P1))>0【此为条件2】。
同时满足以上两个条件时,线段Q1Q2跟线段P1P2才会相交。(其实只要满足这一个实验,两线段相交情况就能确定了,不需要前面的快速排斥实验)
编程里将以上公式转化为坐标运算就可以了。
叉积公式:a × b = (l,m,n) × (o,p,q) = (mq-np,no-lq,lp-mo)
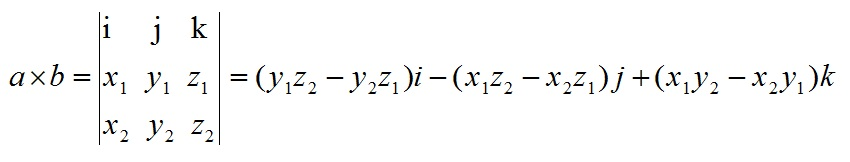
因此条件1等价于:
[(P1x-Q1x)(Q2y-Q1y)-(P1y-Q1y)( Q2x-Q1x)] * [(Q2x-Q1x)(P2y-Q1y)-(Q2y-Q1y)(P2x-Q1x)] > 0
条件2等价于:
[(Q1x-P1x)(P1y-P2y)-(Q1y-P1y)( P2x-P1x)] * [(P2x-P1x)(Q2y-P1y)-(P2y-P1y)(Q2x-P1x)] > 0
求两直线的交点

例题
Segments
Given n segments in the two dimensional space, write a program, which determines if there exists a line such that after projecting these segments on it, all projected segments have at least one point in common.
Input
Input begins with a number T showing the number of test cases and then, T test cases follow. Each test case begins with a line containing a positive integer n ≤ 100 showing the number of segments. After that, n lines containing four real numbers x1 y1 x2 y2 follow, in which (x1, y1) and (x2, y2) are the coordinates of the two endpoints for one of the segments.
Output
For each test case, your program must output “Yes!”, if a line with desired property exists and must output “No!” otherwise. You must assume that two floating point numbers a and b are equal if |a - b| < 10^-8.
Sample Input
3
2
1.0 2.0 3.0 4.0
4.0 5.0 6.0 7.0
3
0.0 0.0 0.0 1.0
0.0 1.0 0.0 2.0
1.0 1.0 2.0 1.0
3
0.0 0.0 0.0 1.0
0.0 2.0 0.0 3.0
1.0 1.0 2.0 1.0
Sample Output
Yes!
Yes!
No!
题意:
给出n条线段,判断是否存在一条线段能经过所有的线段。
思路:
如果存在一条这样的线段,考虑极端情况,这条线段的两点应该是给出的n条线段中的两个点,所以枚举端点去判断是否存在这样一条线段。
判断线段相交需要用到跨立实验的结论。
注意要特判重合的情况,还有n小于等于2时肯定存在一条这样的线段。
#include<iostream>
#include<cmath>
#define ep 1e-8
using namespace std;
int n;
struct point
{
double x, y;
};
struct line
{
point a, b;
}r[105];
//叉乘
double mul(point e, point w, point o)
{
return (w.x-o.x)*(e.y-w.y)-(w.y-o.y)*(e.x-w.x);
}
//跨立实验+判断重合证明相交
//只有跨立实验是无法严格判断相交的,因为存在重合的情况
bool isjudge(point e, point w)
{
if(fabs(e.x - w.x) < ep && fabs(e.y - w.y) < ep) //判断重合
return 0;
for(int i = 0; i < n; ++i)
if(mul(r[i].a, e, w)*mul(r[i].b, e, w) >= ep)
return 0;
return 1;
}
int main()
{
int T;
cin >> T;
while(T--)
{
bool flag = 0;
cin >> n;
for(int i = 0; i < n; ++i)
cin >> r[i].a.x >> r[i].a.y >> r[i].b.x >> r[i].b.y;
if(n <= 2)
{
cout << "Yes!" << endl;
continue;
}
for(int i = 0; i < n && !flag; ++i)
{
if(isjudge(r[i].a, r[i].b))
flag = 1;
//枚举每两个端点
for(int j = i+1; j < n; ++j)
if(isjudge(r[i].a, r[j].a) || isjudge(r[i].a, r[j].b) || isjudge(r[i].b, r[j].a) || isjudge(r[i].b, r[j].b))
flag = 1;
}
if(flag)
cout << "Yes!" << endl;
else
cout << "No!" << endl;
}
return 0;
}
Pick-up sticks
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.

Sample Input
5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0
Sample Output
Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.
Hint
Huge input,scanf is recommended.
题意:
给出n条棍子的两端坐标,按顺序输出最上面的棍子下标号。
思路:
最上面的棍子数后面是不会有和它相交的棍子的,所以两个for循环去判断后面有无同它相交的,无则加入答案数组中。
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
const int N = 1e5 + 5;
int n;
struct point
{
double x, y;
};
struct line
{
point a, b;
}r[N];
int ans[1005];
//叉乘
double mul(point e, point w, point o)
{
return (e.x-o.x)*(w.y-o.y)-(w.x-o.x)*(e.y-o.y);
}
//快速排斥实验+跨立实验证明相交
bool isjudge(line e, line w)
{
if(min(e.a.x, e.b.x) <= max(w.a.x, w.b.x) &&
min(w.a.x, w.b.x) <= max(e.a.x, e.b.x) &&
min(e.a.y, e.b.y) <= max(w.a.y, w.b.y) &&
min(w.a.y, w.b.y) <= max(e.a.y, e.b.y) &&
mul(w.a, e.a, e.b) * mul(e.b, e.a, w.b) >= 0 &&
mul(e.a, w.a, w.b) * mul(w.b, w.a, e.b) >= 0)
return 1;
return 0;
}
int main()
{
while(~scanf("%d", &n) && n)
{
int cnt = 0;
for(int i = 0; i < n; ++i)
scanf("%lf%lf%lf%lf", &r[i].a.x, &r[i].a.y, &r[i].b.x, &r[i].b.y);
for(int i = 0; i < n; ++i)
{
int j;
for(j = i+1; j < n; ++j)
{
if(isjudge(r[i], r[j]))
break;
}
if(j >= n)
ans[cnt++] = i+1;
}
printf("Top sticks:");
for(int i = 0; i < cnt - 1; ++i)
printf(" %d,", ans[i]);
printf(" %d.\n", ans[cnt-1]);
}
return 0;
}
Intersecting Lines
We all know that a pair of distinct points on a plane defines a line and that a pair of lines on a plane will intersect in one of three ways: 1) no intersection because they are parallel, 2) intersect in a line because they are on top of one another (i.e. they are the same line), 3) intersect in a point. In this problem you will use your algebraic knowledge to create a program that determines how and where two lines intersect.
Your program will repeatedly read in four points that define two lines in the x-y plane and determine how and where the lines intersect. All numbers required by this problem will be reasonable, say between -1000 and 1000.
Input
The first line contains an integer N between 1 and 10 describing how many pairs of lines are represented. The next N lines will each contain eight integers. These integers represent the coordinates of four points on the plane in the order x1y1x2y2x3y3x4y4. Thus each of these input lines represents two lines on the plane: the line through (x1,y1) and (x2,y2) and the line through (x3,y3) and (x4,y4). The point (x1,y1) is always distinct from (x2,y2). Likewise with (x3,y3) and (x4,y4).
Output
There should be N+2 lines of output. The first line of output should read INTERSECTING LINES OUTPUT. There will then be one line of output for each pair of planar lines represented by a line of input, describing how the lines intersect: none, line, or point. If the intersection is a point then your program should output the x and y coordinates of the point, correct to two decimal places. The final line of output should read “END OF OUTPUT”.
Sample Input
5
0 0 4 4 0 4 4 0
5 0 7 6 1 0 2 3
5 0 7 6 3 -6 4 -3
2 0 2 27 1 5 18 5
0 3 4 0 1 2 2 5
Sample Output
INTERSECTING LINES OUTPUT
POINT 2.00 2.00
NONE
LINE
POINT 2.00 5.00
POINT 1.07 2.20
END OF OUTPUT
题意:
分别给出两条直线的两个点,去判断这两条直线是重合、平行还是相交,如果是相交的话要求出交点并输出。
ps:这题我做了好久好久好久……主要是重构了很久,而且我后面还发现我看错题了,我以为给的是线段,原来是直线orz。
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
struct point
{
double x, y;
};
struct line
{
point a, b, c, d;
}r[12];
//判断是否共线
bool check(line p)
{
if((int)(p.b.x-p.a.x)*(p.c.y-p.d.y)-(p.c.x-p.d.x)*(p.b.y-p.a.y) == 0)
return 0;
return 1;
}
//判断是重合还是平行
bool check2(line p)
{
if((int)(p.c.x-p.a.x)*(p.c.y-p.d.y)-(p.c.x-p.d.x)*(p.c.y-p.a.y) == 0)
return 0;
return 1;
}
//求两直线交点
double v1, v2;
void count(line p)
{
double b1, b2, d, d1, d2;
b1 = (p.b.y-p.a.y)*p.a.x+(p.a.x-p.b.x)*p.a.y;
b2 = (p.d.y-p.c.y)*p.c.x+(p.c.x-p.d.x)*p.c.y;
d = (p.b.x-p.a.x)*(p.d.y-p.c.y)-(p.d.x-p.c.x)*(p.b.y-p.a.y);
d1 = b2*(p.b.x-p.a.x)-b1*(p.d.x-p.c.x);
d2 = b2*(p.b.y-p.a.y)-b1*(p.d.y-p.c.y);
v1 = d1/d;
v2 = d2/d;
}
int main()
{
int n;
scanf("%d", &n);
for(int i = 0; i < n; ++i)
scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &r[i].a.x, &r[i].a.y, &r[i].b.x, &r[i].b.y, &r[i].c.x, &r[i].c.y, &r[i].d.x, &r[i].d.y);
printf("INTERSECTING LINES OUTPUT\n");
for(int i = 0; i < n; ++i)
{
if(!check(r[i]))
{
if(!check2(r[i]))
printf("LINE\n");
else
printf("NONE\n");
}
else
{
count(r[i]);
printf("POINT %.2lf %.2lf\n", v1, v2);
}
}
printf("END OF OUTPUT\n");
return 0;
}
The Doors
You are to find the length of the shortest path through a chamber containing obstructing walls. The chamber will always have sides at x = 0, x = 10, y = 0, and y = 10. The initial and final points of the path are always (0, 5) and (10, 5). There will also be from 0 to 18 vertical walls inside the chamber, each with two doorways. The figure below illustrates such a chamber and also shows the path of minimal length.
Input
The input data for the illustrated chamber would appear as follows.
2
4 2 7 8 9
7 3 4.5 6 7
The first line contains the number of interior walls. Then there is a line for each such wall, containing five real numbers. The first number is the x coordinate of the wall (0 < x < 10), and the remaining four are the y coordinates of the ends of the doorways in that wall. The x coordinates of the walls are in increasing order, and within each line the y coordinates are in increasing order. The input file will contain at least one such set of data. The end of the data comes when the number of walls is -1.
Output
The output should contain one line of output for each chamber. The line should contain the minimal path length rounded to two decimal places past the decimal point, and always showing the two decimal places past the decimal point. The line should contain no blanks.
Sample Input
1
5 4 6 7 8
2
4 2 7 8 9
7 3 4.5 6 7
-1
Sample Output
10.00
10.06
题意:
按顺序每行第一个数字给出障碍物的x坐标,后面是障碍物的y坐标,一个x坐标有三堵墙。
找出穿过有障碍物房间的最短路径。
思路:
利用判断线段是否相交的方法去求路径。
然后再用弗洛伊德算法/迪杰斯特拉算法去求最短路径。
因为此题的数据较小,所以用的弗洛伊德算法。
#include<iostream>
#include<cmath>
#include<cstdio>
#define eps 1e-8
using namespace std;
const double INF = 1e20;
const int MAXN = 100;
double dis[MAXN][MAXN];
struct Point
{
double x, y;
Point(){}
Point(double _x, double _y)
{
x = _x, y = _y;
}
Point operator -(const Point &b)const
{
return Point(x - b.x, y - b.y);
}
double operator ^(const Point &b)const
{
return x * b.y - y * b.x;
}
double operator *(const Point &b)const
{
return x * b.x + y * b.y;
}
};
struct Line
{
Point s, e;
Line(){}
Line(Point _s, Point _e)
{
s = _s, e = _e;
}
};
Line line[MAXN];
double dist(Point a, Point b)
{
return sqrt((b-a) * (b-a));
}
int sgn(double x)
{
if(fabs(x) < eps)
return 0;
if(x < 0)
return -1;
else
return 1;
}
//判断线段相交
bool inter(Line t1, Line t2)
{
return
max(t1.s.x, t1.e.x) >= min(t2.s.x, t2.e.x) &&
max(t2.s.x, t2.e.x) >= min(t1.s.x, t1.e.x) &&
max(t1.s.y, t1.e.y) >= min(t2.s.y, t2.e.y) &&
max(t2.s.y, t2.e.y) >= min(t1.s.y, t1.e.y) &&
sgn((t2.s-t1.s)^(t1.e-t1.s)) * sgn((t2.e - t1.s)^(t1.e-t1.s)) <= 0 &&
sgn((t1.s-t2.s)^(t2.e-t2.s)) * sgn((t1.e-t2.s)^(t2.e-t2.s)) <= 0;
}
int main()
{
int n;
double x, y1, y2, y3, y4;
while(~scanf("%d", &n) && n != -1)
{
for(int i = 1; i <= n; ++i)
{
scanf("%lf%lf%lf%lf%lf", &x, &y1, &y2, &y3, &y4);
line[2*i-1] = Line(Point(x, y1), Point(x, y2));
line[2*i] = Line(Point(x, y3), Point(x, y4));
}
//初始化图
for(int i = 0; i <= 4*n+1; ++i)
{
for(int j = 0; j <= 4*n+1; ++j)
{
if(i == j)
dis[i][j] = 0;
else
dis[i][j] = INF;
}
}
for(int i = 1; i <= 4*n; ++i)
{
int lid = (i+3) / 4;
bool flag = true;
Point tmp;
if(i&1)
tmp = line[(i+1)/2].s;
else
tmp = line[(i+1)/2].e;
for(int j = 1; j < lid; ++j)
{
if(inter(line[2*j-1], Line(Point(0, 5), tmp)) == false &&
inter(line[2*j], Line(Point(0, 5), tmp)) == false)
flag = false;
}
if(flag)
dis[0][i] = dis[i][0] = dist(Point(0, 5), tmp);
flag = true;
for(int j = lid + 1; j <= n; ++j)
{
if(inter(line[2*j-1], Line(Point(10, 5), tmp)) == false &&
inter(line[2*j], Line(Point(10, 5), tmp)) == false)
flag = false;
}
if(flag)
dis[i][4*n+1] = dis[4*n+1][i] = dist(Point(10, 5), tmp);
}
for(int i = 1; i <= 4*n; ++i)
{
for(int j = i+1; j <= 4*n; ++j)
{
int lid1 = (i+3)/4;
int lid2 = (j+3)/4;
bool flag = true;
Point p1, p2;
if(i&1)
p1 = line[(i+1)/2].s;
else
p1 = line[(i+1)/2].e;
if(j&1)
p2 = line[(j+1)/2].s;
else
p2 = line[(j+1)/2].e;
for(int k = lid1 + 1; k < lid2; ++k)
{
if(inter(line[2*k-1], Line(p1, p2)) == false &&
inter(line[2*k], Line(p1, p2)) == false)
flag = false;
}
if(flag)
dis[i][j] = dis[j][i] = dist(p1, p2);
}
}
bool flag = true;
for(int i = 1; i <= n; ++i)
{
if(inter(line[2*i-1], Line(Point(0, 5), Point(10, 5))) == false &&
inter(line[2*i], Line(Point(0, 5), Point(10, 5))) == false)
flag = false;
}
if(flag)
dis[0][4*n+1] = dis[4*n+1][0] = 10;
//弗洛伊德算法求最短路径
for(int k = 0; k <= 4*n+1; ++k)
{
for(int i = 0; i <= 4*n+1; ++i)
{
for(int j = 0; j <= 4*n+1; ++j)
{
if(dis[i][k] + dis[k][j] < dis[i][j])
dis[i][j] = dis[i][k] + dis[k][j];
}
}
}
printf("%.2lf\n", dis[0][4*n+1]);
}
return 0;
}
Morley’s Theorem
Morleys theorem states that that the lines trisecting the angles of an arbitrary plane triangle meet at the vertices of an equilateral triangle. For example in the figure below the trisectors of angles A, B and C has intersected and created an equilateral triangle DEF.
Of course the theorem has various generalizations, in particular if all of the trisectors are intersected one obtains four other equilateral triangles. But in the original theorem only trisectors nearest to BC are allowed to intersect to get point D, trisectors nearest to CA are allowed to intersect point E and trisectors nearest to AB are intersected to get point F. Trisector like BD and CE are not allowed to intersect. So ultimately we get only one equilateral triangle DEF. Now your task is to find the Cartesian coordinates of D, E and F given the coordinates of A, B, and C.

Input
First line of the input file contains an integer N (0 < N < 5001) which denotes the number of test cases to follow. Each of the next lines contain six integers XA, YA, XB, YB, XC , YC . This six integers actually indicates that the Cartesian coordinates of point A, B and C are (XA, YA),(XB, YB) and (XC , YC ) respectively. You can assume that the area of triangle ABC is not equal to zero, 0 ≤ XA, YA, XB, YB, XC , YC ≤ 1000 and the points A, B and C are in counter clockwise order.
Output
For each line of input you should produce one line of output. This line contains six floating point numbers XD, YD, XE, YE, XF , YF separated by a single space. These six floating-point actually means
that the Cartesian coordinates of D, E and F are (XD, YD),(XE, YE) ,(XF , YF ) respectively. Errors less than 10−5 will be accepted.
Sample Input
2
1 1 2 2 1 2
0 0 100 0 50 50
Sample Output
1.316987 1.816987 1.183013 1.683013 1.366025 1.633975
56.698730 25.000000 43.301270 25.000000 50.000000 13.397460
题意:三角形每个内角的三等分线相交的三角形为等边三角形,求交点坐标。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct Point
{
double x, y;
Point(double x = 0, double y = 0):x(x), y(y){}
};
typedef Point v;
int t;
Point A, B, C, D, E, F;
v operator +(v A, v B)
{
return v(A.x + B.x, A.y + B.y);
}
v operator -(v A, v B)
{
return v(A.x - B.x, A.y - B.y);
}
v operator *(v A, double p)
{
return v(A.x * p, A.y * p);
}
v operator /(v A, double p)
{
return v(A.x / p, A.y / p);
}
double Dot(v A, v B)
{
return A.x*B.x + A.y*B.y;
}
double Length(v A)
{
return sqrt(Dot(A, A));
}
double Angle(v A, v B)
{
return acos(Dot(A, B) / Length(A) / Length(B));
}
v Rotate(v A, double rad)
{
return v(A.x*cos(rad) - A.y*sin(rad), A.x*sin(rad) + A.y*cos(rad));
}
double Cross(v A, v B)
{
return A.x*B.y - A.y*B.x;
}
Point Get_LineIntersection(Point P, v V, Point Q, v W)
{
v u = P - Q;
double t = Cross(W, u) / Cross(V, W);
return P + V*t;
}
Point GetD(Point A, Point B, Point C)
{
v v1 = C - B;
double a1 = Angle((A-B), v1);
v1 = Rotate(v1, a1/3);
v v2 = B - C;
double a2 = Angle((A-C), v2);
v2 = Rotate(v2, -a2/3);
return Get_LineIntersection(B, v1, C, v2);
}
int main()
{
scanf("%d", &t);
while(t--)
{
scanf("%lf%lf%lf%lf%lf%lf", &A.x, & A.y, &B.x, &B.y, &C.x, &C.y);
D = GetD(A, B, C);
E = GetD(B, C, A);
F = GetD(C, A, B);
printf("%.6f %.6f %.6f %.6f %.6f %.6f\n", D.x, D.y, E.x, E.y, F.x, F.y);
}
return 0;
}






















 2120
2120











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








