如何评价2023年国际高校数学建模竞赛B题？

问题1：在三星堆发现的一个外圆直径为85厘米，内圆直径为40厘米（假设）的青铜车轮，青铜车轮有5条车轴（射线），5条内弧线本质是双曲线，顶点与内圆相切，内弧双曲线的切线为与其相邻的车轴（射线），请以青铜太阳轮的中心为坐标原点，计算出青铜太阳轮与弧线对应的五条内“射线”的曲线方程，建立数学模型，推导出内弧线的一般方程，并根据一般方程画出四条、六条、八条、十二条射线的青铜太阳轮图案（使用matlab）。思路按照以下：

目前已写出公式推导过程、代码和求解结果，相关文件下载见文末地址[1]

很明显，曲线为双曲线，顶点在内圆上，双曲线的切线为2条射线。首先我们来复习一下双曲线：

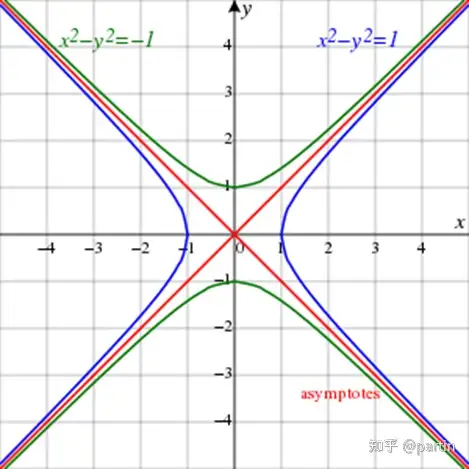
双曲线由分开两个焦点的两个分离的称为臂或分支的曲线构成。随着到焦点的距离的变大，双曲线就越逼近称为渐近线的两条线。渐近线交叉于双曲线的中点，并对于东西开口的双曲线有斜率±b/a，对于北南开口的双曲线有斜率±a/b。