【python库mpi4py的蒙特卡洛法求定积分的并行与串行实现】

置顶 kugua527

已于 2023-07-04 11:20:17 修改

阅读量529

点赞数 1

分类专栏：并行计算数值积分文章标签：概率论数学建模 python numpy 算法

于 2023-07-02 22:39:38 首次发布

本文链接：https://blog.csdn.net/qq_52597811/article/details/131502549

版权

并行计算同时被 2 个专栏收录

2 篇文章 0 订阅

订阅专栏

数值积分

1 篇文章 0 订阅

订阅专栏

蒙特卡罗模拟方法：是一种计算技术，用于通过统计抽样研究和预测复杂系统的行为。它最早是由数学家斯坦尼斯瓦夫·乌拉姆和约翰·冯·诺依曼在20世纪40年代开发的，用于解决物理学中的复杂问题，例如中子在核链式反应中的行为。蒙特卡洛模拟包括生成大量可能的场景，称为“随机样本”，以便对复杂系统的行为进行建模和预测。通常，这些随机样本是使用随机数生成器或通过模拟随机性的其他方式生成的。

mpi4py：mpi4py库是一个Python包，它为分布式并行计算的消息传递接口（MPI）标准提供了一个高效且用户友好的接口。MPI是一种广泛使用的规范，用于高性能计算（HPC）和并行计算环境中进程之间的消息传递和通信。mpi4py库使Python开发人员能够利用MPI的强大功能，并利用跨多个处理器、节点或集群的并行处理。mpi4py针对性能进行了优化，旨在最大限度地减少从Python调用MPI函数的相关开销。它建立在高质量和高效的C级MPI绑定之上，使用户能够充分利用基于MPI的HPC系统的性能。mpi4py与大多数流行的MPI实现兼容，如Open MPI、MPICH和Intel MPI。这意味着您可以使用mpi4py来开发在各种HPC平台上无缝运行的并行Python应用程序。

配置环境：

下载MicrosoftMPI：点击此处下载；安装mpi4py库：在终端运行pip install mpi4py，或者使用anaconda的conda install mpi4py命令。

一、先看最简单的情况，也就是函数f在积分域上恒为正值的情况。

下面以定积分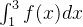 $eq?%5Cint_%7B1%7D%5E%7B3%7Df%28x%29dx$ 为例,其中 $eq?f%28x%29%3Dx%5E%7B3%7D-4x%5E%7B2%7D+5x-2e%5E%7Bx%5E%7B2%7D-3x%7D$

1.1 蒙特卡洛模拟求定积分的思想

取y=maxf(x)，y=0，x=a（积分下限），x=b（积分上限）围成的矩形域之内的点（x,y），如果f(x)>y，则该点位于y=f(x)，y=0，x=a，x=b所围成的区域之内（下面称之为函数域），那么计数器加1；
重复第1步n(模拟次数)次，之后得到随机点位于函数域之内的概率；
将2得到的概率乘上矩形域的面积，就可以得到数值积分了。

1.2 求函数最值

在上面的计算中存在一个问题，一个不知道该函数在[a,b]区间的最大值maxf(x)，所以还要设计一个求函数最大值的程序。

我们知道函数在最值处的导数值为0，所以只需要将所有区间内导数值为0的点找出来，然后带入函数并与边界值比较就可以得到函数的最大值了。导数的计算又不是一件容易的事。

在这里采用离散化区间并用向前差分代替导数的思想：

将区间离散化为： $eq?x_%7B0%7D%3Da%2Cx_%7B1%7D%2Cx_%7B2%7D...x_%7Bk-1%7D%2Cx_%7Bk%7D%3Db$ ；
用向前差分代替导数 $eq?f%5E%7B%27%7D%28x_%7Bi%7D%29%3D%5Cfrac%7Bx_%7Bi+1%7D-x_%7Bi%7D%7D%7Bdx%7D$ , $eq?dx$ 为离散化点之间的距离，然后找到导函数值之积为负的相邻两点（零点存在性定理），取算术平均，就得到了函数 $eq?f%28x%29$ 的近似稳定点了。

dx越小得到的近似稳定点误差越小，之后将所有近似稳定点和边界值带入函数就可以得到函数的近似最大值了。同样的道理，也可以求出函数的近似最小值。也可以用中心差分代替向前差分来求，会有更高的精度。这里没有用求函数最值的库，不然就没意思了。

向前差分法求函数在区间的最大值与最小值代码块如下：

import numpy as np
import random
import math
def func(x):
    y = x ** 3 - 4 * x ** 2 + 5 * x - 2 * math.exp(x ** 2 - 3 * x)
    return y
a, b = 1, 3
stable_p=[]
dx = 0.001
lst_x = [i for i in np.arange(a, b+2*dx, dx)]
lst_dy = []
for i in range(len(lst_x)):
    if i != len(lst_x)-1:
        dy = (func(lst_x[i+1]) - func(lst_x[i])) / dx
        lst_dy.append(dy)
        if i != 0 and lst_dy[i-1] * lst_dy[i] < 0:
            stable_p.append(lst_x[i] - dx/2)                                       
value = [func(a), func(b)]  # 极值与边界值列表
for j in stable_p:
    value.append(func(j))                                               
maxi, mini = max(value), min(value)                           
print('函数在[{:},{:}]上稳定点为：{:}'.format(a, b, stable_p))
print('函数在[{:},{:}]上最大值为为：{:4f}，最小值为：{:4f}'.format(a, b, maxi, mini))

结果如下：

函数在[1,3]上稳定点为：[1.1134999999999875, 1.7094999999999219] 
函数在[1,3]上最大值为为：4.000000，最小值为：1.633509

下面是f(x)的导数图像：

从图像可以看到导数为0的点大约在1.112与1.705附近，所以求出的稳定点是比较准确的。

下面是函数f(x)的图像：

算出可以看出最大值与最小值基本准确。

1.3 代码实现

将得到函数的最大值广播到所有进程：

maxi = comm.bcast(maxi if rank == 0 else None, root=0)  # 主进程广播maxi到其他进程

各个进程得到函数最大值后开始模拟：

# 各进程开始模拟 
random.seed(0) 
cnt = 0 
if rank == 0:
     for i in range(zero_man):
         x, y = a + (b - a) * random.random(), maxi * random.random()  # 生成矩形区域内的点
         if func(x) > y:
             cnt += 1 
else:
     for i in range(normal_man):
         x, y = a + (b - a) * random.random(), maxi * random.random()  # 生成矩形区域内的点
         if func(x) > y:
             cnt += 1

通过规约将每个进程的cnt加到主进程中：

cnt = comm.reduce(cnt, root=0, op=MPI.SUM)  # 将所有进程中的cnt相加到主进程中

主进程计算概率和矩形域面积，最后两者相乘得到数值积分：

if rank == 0:
     p = cnt / n
     Square = maxi * (b - a)
     positive_funcs_int = p * Square
     tb = time.time() - t0b
     print('模拟次数：{:}，积分值为：{:}'.format(n, positive_funcs_int))

为了和串行程序做对比，在最后加了串行程序，并输出加速比和效率以作并行计算的分析：

# 开始串行
cnt = 0     
t0c = time.time()     
for i in range(n):    
     x, y = a + (b - a) * random.random(), maxi * random.random()  # 生成矩形区域内的点
     if func(x) > y:       
        cnt += 1
p = cnt / n     
Square = maxi * (b - a)     
positive_funcs_int = p * Square     
tc = time.time() - t0c     
print('并行时间：{:0<10.5f}秒'.format(tb))     
print('串行时间：{:0<10.5f}秒'.format(tc))     
print('加速比：{:5f}'.format(tc/tb))     
print('效率：{:5f}'.format(tc/tb/size))

1.4 结果验证及并行性分析

结果验证：

下面以模拟次数一千万次，进程数8为例，在终端调至文件所在路径并输入：

mpiexec -np 8 python int_mpi.py

结果如下：

模拟次数：10000000，积分值为：4.3613472 
并行时间：2.90684000秒 
串行时间：13.9555400秒 
加速比：4.800939 
效率：60.011739%

使用MATLAB的符号积分计算函数int可以得到一个误差很小的积分值

syms f(x)
f(x)=x^3-4*x^2+5*x-2*exp(x^2-3*x);
int_f=double(int(f,[1,3]))
%输出值为4.361952754808197

使用蒙特卡洛模拟得到的积分值相对误差小于万分之一。

并行分析：模拟次数分别为一万，十万，一百万，一千万；进程数分别为4，8，12，16。

进程数为8时，串行并行用时对比：

二、也是一种简单的情况，函数f在积分域上恒为负值

在情况一得到了函数的最小值，主进程改广播最小值，并将其他为最大值的地方改成最小值,判断随机点是否位于函数域内的符号反号，即变成<,最后在得到的积分的那步加上一个负号就可以了，具体改动如下：

mini = comm.bcast(maxi if rank == 0 else None, root=0)  # 主进程广播maxi到其他进程

if rank == 0:
     for i in range(zero_man):
         x, y = a + (b - a) * random.random(), mini * random.random()  # 生成矩形区域内的点
         if func(x) < y:
             cnt += 1
else:
     for i in range(normal_man):
         x, y = a + (b - a) * random.random(), mini * random.random()  # 生成矩形区域内的点
         if func(x) < y:
             cnt += 1

negative_funcs_int = - p * Square

三、一般情况，即函数在积分域上变号

一般情况下，对 $f(x)$ 作一个变换 $g(x)=f(x)-minf(x)$ ,则g(x)在积分区域上是恒大于零的，这时候套用情况一就得到了定积分 $\int_{a}^{b}g(x)dx$ ,由定积分的性质可以得到 $\int_{a}^{b}f(x)dx=\int_{a}^{b}g(x)dx+(b-a)minf(x)$

对代码改动部分如下啊：

maxi, mini = max(value), min(value)     
maxi = comm.bcast(maxi if rank == 0 else None, root=0)  # 主进程广播最大值到其他进程
mini = comm.bcast(mini if rank == 0 else None, root=0)  # 主进程广播最小值到其他进程

if rank == 0: 
    for i in range(zero_man):
        x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点
        if func(x) - mini > y:
            cnt += 1 
else:
    for i in range(normal_man):
        x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点
        if func(x) -mini > y:
            cnt += 1

Square = (maxi - mini) * (b - a)     
funcs_int =p * Square + mini * (b - a)

下面以积分 $\int_{1}^{3}f(x)dx$ ,其中 $f(x)=(4x^{2}-5x-2e^{x^{2}-3x})sinx$ 为例，并验证正确性。一亿次模拟运行结果如下：

模拟次数：100000000，积分值为：2.139715230135973 
并行时间：46.0982100秒 
串行时间：205.280740秒 
加速比：4.453118 
效率：55.663969%

函数图像如下：

使用MATLAB符号积分得到该积分的较精确值为2.141742485969445。

相对误差大约为0.947‰

四、蒙特卡洛模拟求定积分并行程序分析

用蒙特卡洛求数值积分的误差不太好估计，矩形域面积和模拟次数有关，当矩形域面积过大时，就要用更多的点才能得到更准确的概率以得到较准确的积分值，就第一种情况区间面积为8，模拟一百万次比较准确；

该并行程序的算法时间复杂度要主要取决于积分函数，因为每次模拟都要调用函数，如果函数比较复杂，计算量就上来了，但每次调用函数计算量固定，随机数生成是比较快的，所以总的时间复杂度为 $O(n)$ ,由情况一的运行情况也可以看出程序的时间复杂度为 $O(n)$ 。

蒙特卡洛模拟是可并行性很好的算法，因为各个进程之间没有交叉任务，只需要各干各的最后汇总即可。

五、代码汇总

5.1 一般情况下的串行并行的合并程序：

from mpi4py import MPI 
import random 
import numpy as np 
import math 
import time 
# 数值积分(x^2-5x-2exp(x^2-3x))sin(x^2),积分区间为1到3.
# 精确值2.141742485969445.


def func(x):
     y = math.sin(x ** 2) * (4 * x ** 2 - 5 * x - 2 * math.exp(x ** 2 - 3 * x))
     return y


comm = MPI.COMM_WORLD rank = comm.Get_rank()  # 获得线程号 
size = comm.Get_size()  # 获得进程数 
a, b = 1, 3  # 积分区间 
n = 10000000  # 模拟次数 
normal_man = n // size 
t0b = time.time() 
if rank == 0:
    # 主进程分配任务
    zero_man = n - normal_man * (size - 1)
    # 计算函数最大值
    dy_dic = {}  # 各点的向前差分
    stable_p = []  # 稳定点
    dx = 0.001
    lst_x = [i for i in np.arange(a, b+dx, dx)]
    lst_dy = []     for i in range(len(lst_x)):
        if i != len(lst_x)-1:
            dy = (func(lst_x[i+1]) - func(lst_x[i])) / dx             
            lst_dy.append(dy)
            if i != 0 and lst_dy[i-1] * lst_dy[i] < 0:                   
                stable_p.append(lst_x[i] - dx/2)
    value = [func(a), func(b)]  # 极值与边界值列表
    for j in stable_p:
        value.append(func(j))
    maxi, mini= max(value), min(value)
maxi = comm.bcast(maxi if rank == 0 else None, root=0)  # 主进程广播最大值到其他进程
mini = comm.bcast(mini if rank == 0 else None, root=0)  # 主进程广播最小值到其他进程 
# 各进程开始模拟 
random.seed(0) 
cnt = 0 
if rank == 0:
    for i in range(zero_man):
        x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点
        if func(x) - mini > y: 
            cnt += 1 
else: 
    for i in range(normal_man): 
        x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点 
        if func(x) - mini > y: 
            cnt += 1 cnt = comm.reduce(cnt, root=0, op=MPI.SUM)  # 将所有进程中的cnt相加到主进程中 
if rank == 0: 
    p = cnt / n 
    Square = (maxi - mini) * (b - a) 
    funcs_int = p * Square + mini * (b - a)
    tb = time.time() - t0b 
    print('模拟次数：{:}\n积分值为：{:0<10.10f}'.format(n, funcs_int)) 
    # 开始串行 
    cnt = 0 
    t0c = time.time() 
    for i in range(n): 
        x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点 
        if func(x) - mini > y: 
            cnt += 1 
    p = cnt / n 
    Square = (maxi - mini) * (b - a) 
    funcs_int =p * Square + mini * (b - a)
    tc = time.time() - t0c 
    print('并行时间：{:0<10.10f}秒'.format(tb)) 
    print('串行时间：{:0<10.10f}秒'.format(tc)) 
    print('加速比：{:0<10.10f}'.format(tc/tb)) 
    print('效率：{:0<10.9f}%'.format(tc/tb/size*100))

5.2 一般情况下的并行程序：

from mpi4py import MPI  
import random  
import numpy as np  
import math  
import time  
# 数值积分(x^2-5x-2exp(x^2-3x))sin(x^2),积分区间为1到3. 
# 精确值2.141742485969445. 

  
def func(x):  
    y = math.sin(x ** 2) * (4 * x ** 2 - 5 * x - 2 * math.exp(x ** 2 - 3 * x)) 
    return y  

 
comm = MPI.COMM_WORLD rank = comm.Get_rank()  # 获得线程号  
size = comm.Get_size()  # 获得进程数  
a, b = 1, 3  # 积分区间  
n = 10000000  # 模拟次数  
normal_man = n // size  
t0b = time.time()  
if rank == 0: 
    # 主进程分配任务 
    zero_man = n - normal_man * (size - 1) 
    # 计算函数最大值 
    dy_dic = {}  # 各点的向前差分 
    stable_p = []  # 稳定点 
    dx = 0.001 
    lst_x = [i for i in np.arange(a, b+dx, dx)]  
    lst_dy = [] 
    for i in range(len(lst_x)):    
        if i != len(lst_x)-1:   
            dy = (func(lst_x[i+1]) - func(lst_x[i])) / dx
            lst_dy.append(dy)  
            if i != 0 and lst_dy[i-1] * lst_dy[i] < 0:
                stable_p.append(lst_x[i] - dx/2)
    value = [func(a), func(b)]  # 极值与边界值列表 
    for j in stable_p:  
        value.append(func(j)) 
    maxi, mini= max(value), min(value) 
maxi = comm.bcast(maxi if rank == 0 else None, root=0)  # 主进程广播最大值到其他进程 
mini = comm.bcast(mini if rank == 0 else None, root=0)  # 主进程广播最小值到其他进程 

# 各进程开始模拟  
random.seed(0)  
cnt = 0  
if rank == 0: 
    for i in range(zero_man): 
        x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点  
        if func(x) - mini > y:   
            cnt += 1  
else: 
    for i in range(normal_man):  
        x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点   
        if func(x) - mini > y:  
            cnt += 1 
cnt = comm.reduce(cnt, root=0, op=MPI.SUM)  # 将所有进程中的cnt相加到主进程中 

# 主进程计算结果 
if rank == 0: 
    p = cnt / n 
    Square = (maxi - mini) * (b - a)  
    funcs_int = p * Square + mini * (b - a)  
    tb = time.time() - t0b  
    print('模拟次数：{:}\n积分值为：{:0<10.10f}'.format(n, funcs_int)) 
    print('并行时间：{:0<10.10f}秒'.format(tb))

5.3 一般情况下的串行程序(一般程序，即不需要下mpi4py和MicrosoftMPI，可直接运行)：

import random  
import numpy as np  
import math  
import time  
# 数值积分(x^2-5x-2exp(x^2-3x))sin(x^2),积分区间为1到3. 
# 精确值2.141742485969445.  
# 初始化

 
def func(x): 
    y = math.sin(x ** 2) * (4 * x ** 2 - 5 * x - 2 * math.exp(x ** 2 - 3 * x))
        return y


a, b = 1, 3  # 积分区间
n = 10000000  # 模拟次数 

# 求函数最值 
dy_dic = {}  # 各点的向前差分     
stable_p = []  # 稳定点     
dx = 0.001     
lst_x = [i for i in np.arange(a, b+dx, dx)]     
lst_dy = []     
for i in range(len(lst_x)):         
    if i != len(lst_x)-1:
        dy = (func(lst_x[i+1]) - func(lst_x[i])) / dx 
        lst_dy.append(dy)
        if i != 0 and lst_dy[i-1] * lst_dy[i] < 0:                                    
            stable_p.append(lst_x[i] - dx/2)
    value = [func(a), func(b)]  # 极值与边界值列表
for j in stable_p:
    value.append(func(j))
maxi, mini= max(value), min(value)

      
# 开始模拟     
cnt = 0      
t0c = time.time()      
for i in range(n):     
    x, y = a + (b - a) * random.random(), (maxi - mini) * random.random()  # 生成矩形区域内的点
    if func(x) - mini > y:
        cnt += 1 
p = cnt / n  
Square = (maxi - mini) * (b - a)  
funcs_int =p * Square + mini * (b - a) 
tc = time.time() - t0c      
print('模拟次数：{:}\n积分值为：{:0<10.10f}'.format(n, funcs_int))
print('运行时间：{:0<10.10f}秒'.format(tc))

有任何问题欢迎发表评论，我看到第一时间会回复。