机器学习实验一-多项式拟合

一、实验目的

掌握最小二乘法求解（无惩罚项的损失函数）、掌握加惩罚项（2范数）的损失函数优化、梯度下降法、共轭梯度法、理解过拟合、克服过拟合的方法(如加惩罚项、增加样本)

• 实验要求及实验环境

实验要求：

1. 生成数据，加入噪声；

2. 用高阶多项式函数拟合曲线；

3. 用解析解求解两种loss的最优解（无正则项和有正则项）

4. 优化方法求解最优解（梯度下降，共轭梯度）；

5. 用你得到的实验数据，解释过拟合。

6. 用不同数据量，不同超参数，不同的多项式阶数，比较实验效果。

7. 语言不限，可以用matlab，python。求解解析解时可以利用现成的矩阵求逆。梯度下降，共轭梯度要求自己求梯度，迭代优化自己写。不许用现成的平台，例如pytorch，tensorflow的自动微分工具。

实验环境：

Windows 10 ；python 3.9.7；jupyter notebook 6.4.12

三、设计思想（本程序中的用到的主要算法及数据结构）

由高数中的泰勒级数可知，足够高阶的多项式可以拟合任意函数。因此，我们可以用多项式来拟合正弦函数sin(2πX)。在m阶多项式中，有m+1个待定系数，m+1个系数（由低到高）组成的（列）向量记作w。

                                   

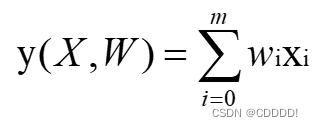
为了确定w，分别使用最小二乘法与梯度下降法。

 

3.1 最小二乘法：

    最下二乘法的代价函数为：

                      

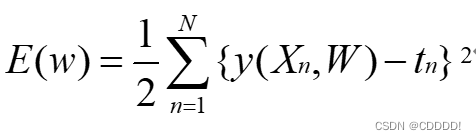
使用最小二乘法其中，X为多项式中各个未知项代入观测数据求得的矩阵，若记Xi为X的第i行的向量，则Xi[j]为第i个观测数据xi的j次方，记有n组观测数据，多项式最高次为m，易知X的维度为n * (m+1)。Y为观测标签向量。即Y[j]为第j组观测数据的标签值（即y值）。从而问题转化为：求向量w，使得E(w)最小。

        下面分别分析添加惩罚项与否时的w取值。首先，我们令损失函数导数等于0，求此时的w。

       

 

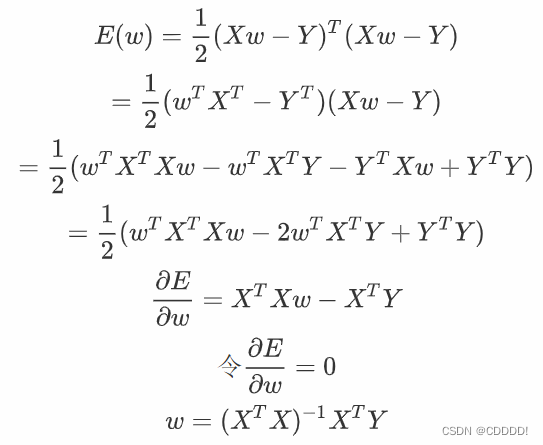
     图1-1 无惩罚项时的w求解过程

在前面的求解过程中，没有加惩罚项，此时随着阶数m的增大，w*往往具有较大的绝对值，从而赋予多项式函数E ( w )更强的变化能力。往往会为了更加贴合训练集中样本点，使得 w各维数值绝对值很大、很复杂，将一些不属于训练集的特征（如：噪声的影响）都学习到了，发生了过拟合。因此，我们可以增加惩罚项，迫使 w*的绝对值没有那么大。添加惩罚项，令损失函数导数等于0，求此时的w。

      

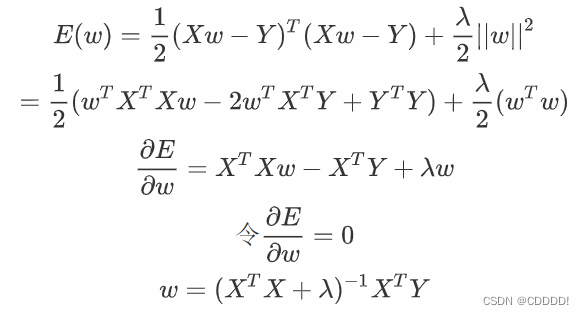
        图1-2 有惩罚项时的w求解过程

3.1.2 最小二乘法核心算法如图所示：

            图1-3 最小二乘法核心算法

3.2 梯度下降法

梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处，如图1-3所示：

            

                          图1-4 梯度下降法示例

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向。

我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。

3.2.1 梯度下降法算法实现：

核心部分如图所示：

                    图3.2.1 梯度下降法核心算法

3.3 共轭梯度法

首先，我们考虑线性对称正定方程组： ，其等价于求解如下凸优化问题：

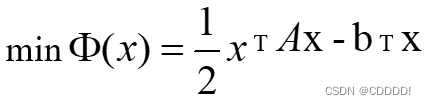
其中。

 于是，假设已经有了一组共轭向量，我们把未知量表示为它们的线性组合，我们希望能够寻找一组系数，去极小化

           

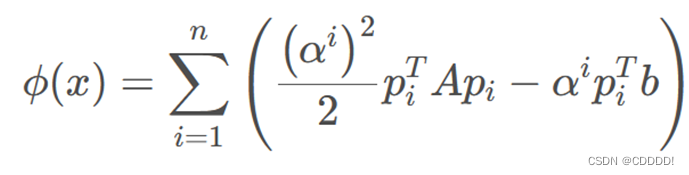
求和中的每一项都是独立的，极小化之，那么我们就可以得到

                     

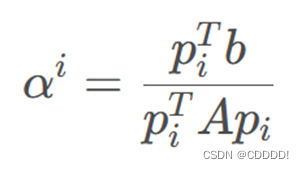
通过共轭方向，把一个 n 维问题，拆解成了 n 个一维问题。

其伪代码如下：

3.2.2 共轭梯度法算法实现：

其核心部分如下：

  图3.2.2 共轭梯度法核心代码

• 实验结果与分析

4.1 使用解析解求解不含有正则项的 loss 函数
4.1.1 求解最优解
   根据如上算法，我们在使用 3 阶多项式的时候得到了如图4.1的曲线，同时得到了最终的解向量w，将该解向量与x轴坐标阶数矩阵点乘，得到如图4.1的曲线，它的 RMS 值是：0.074

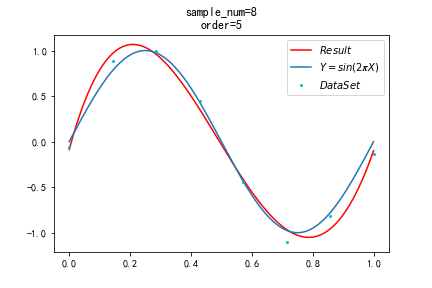
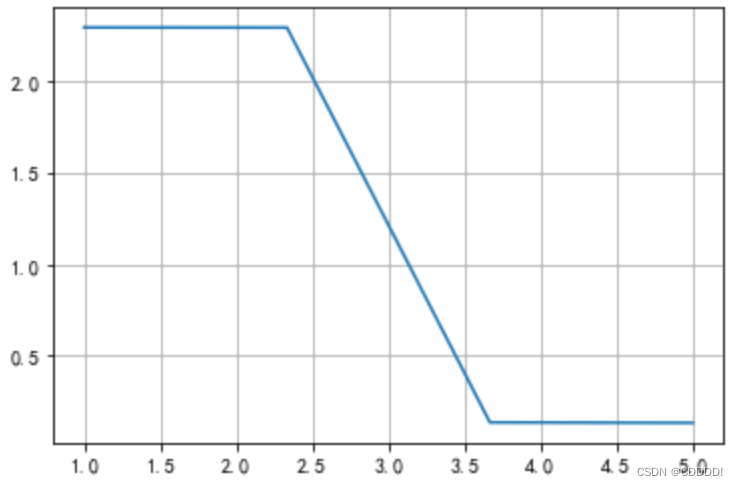
    图4.1 5阶多项式拟合曲线                图4.3 5阶多项式拟合loss值

4.1.2 过拟合

在这种情况下，非常容易出现过拟合的情况，只要将多项式的阶数值调到一个较大的时候，就会出现过拟合的现象，如图4.3所示，出现过拟合的时候该模型过多地拟合了图中的数据点（此时 RMS 为0.004）以至于该模型对其他的输入预测能力很弱。出现过拟合的时候该多项式的曲线很明显并不是一个和 sin(2πx) 相近的曲线。其损失函数如图4.4所示。

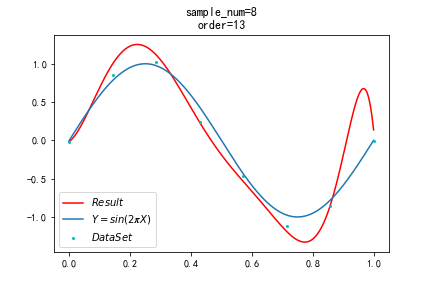
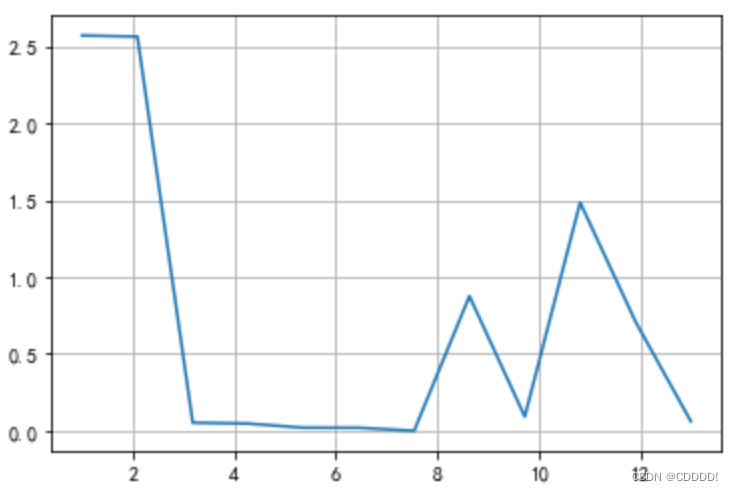
       图4.3 13阶多项式拟合曲线        图4.4 13阶多项式拟合loss值

4.1.3 使用不用的数据量，不同的多项式阶数结果比较

为了完成本小节的实验，我选取了 M = 3,5,7,9,12共让该模型跑5次，得到随着 M阶数的变化,每一次的结果如图4.5所示。

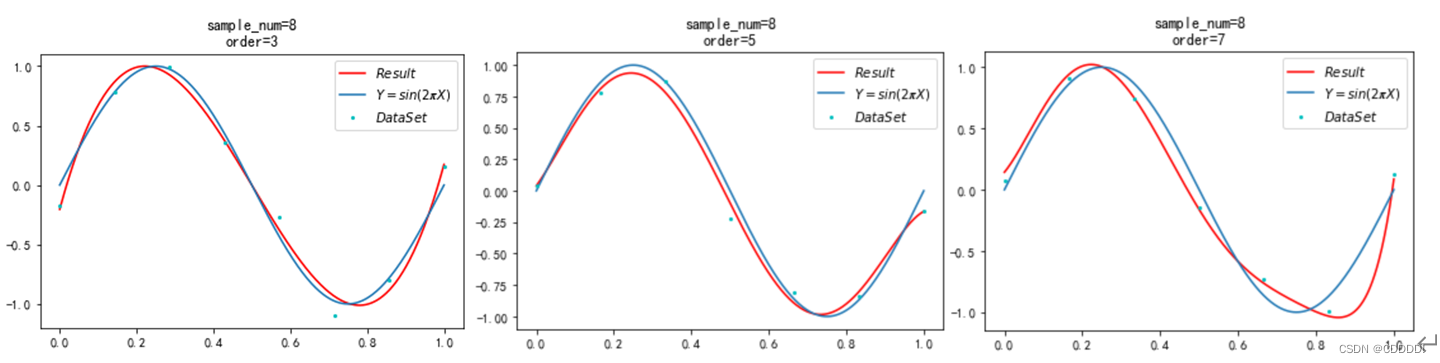
1. 3阶多项式                                       (b) 5阶多项式                            (c) 7阶多项式

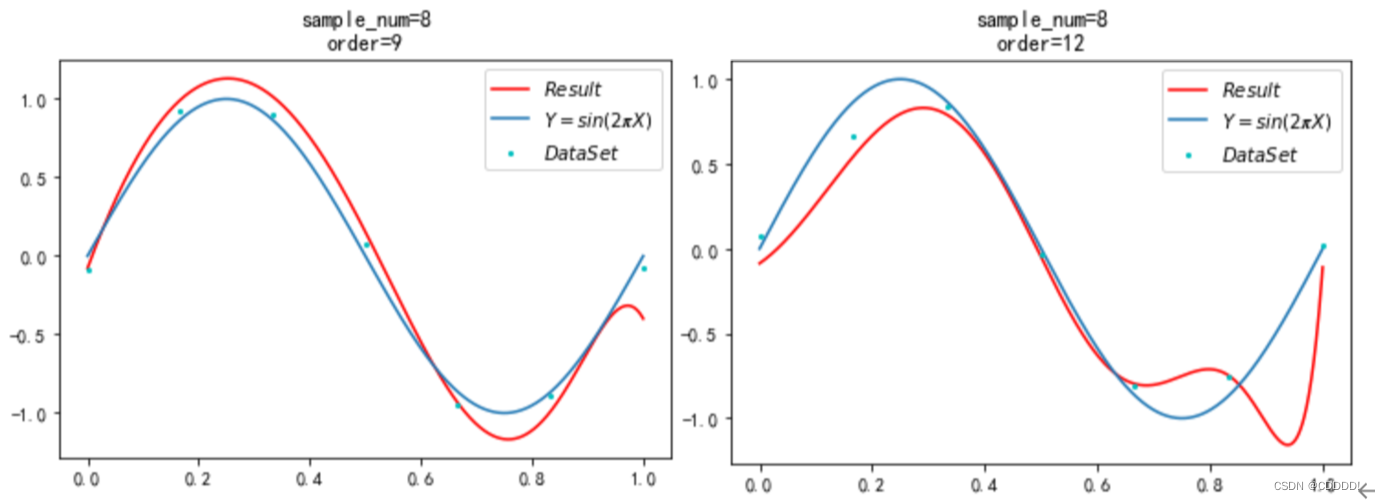
              (d) 9阶多项式                                                            (e) 12阶多项式

       图4.5 不同阶数多项式下的拟合效果

可以看出，不改变数据集大小的情况下，随着模型复杂度的上升，出现了过拟合的现象。

对于不同的数据集大小，我分别选取了10，30，60，150，300的数据集大小，在多项式项数设置为5的时候进行了5次实验，得到的结果如图4.7所示。

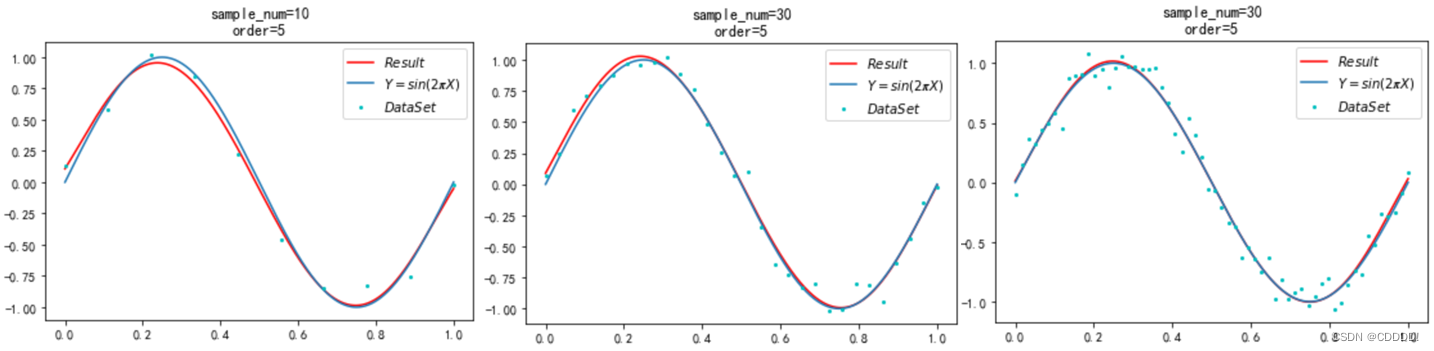
1. Sample=10                                    (b) Sample=30                               (c) Sample=60

 

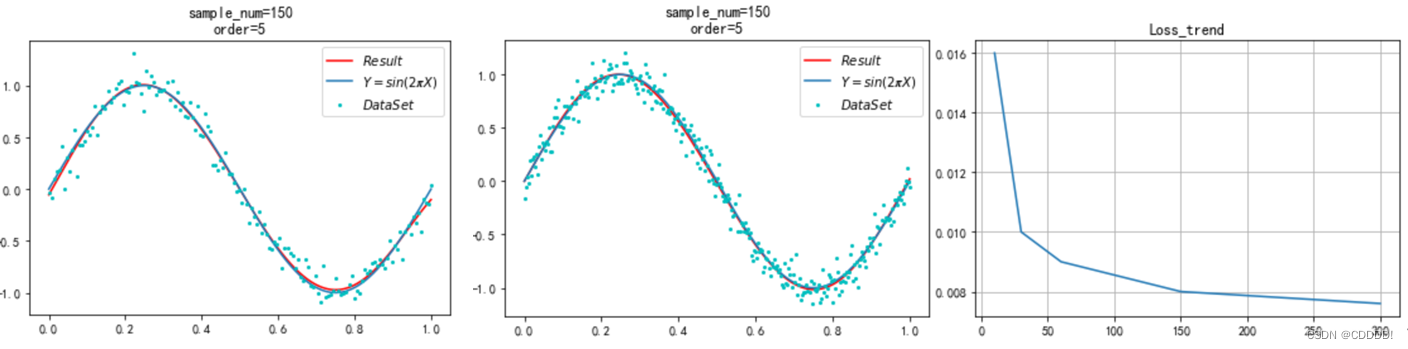
        (d) Sample=150                         (e) Sample=300                          (f) 损失函数随数据集大小变化

图4.6 不同数据集下的多项式拟合效果

可以看出，当数据集大小开始增加的时候，模型预测的曲线逐渐向正确的 sin(2πx) 靠拢，说明增加数据集大小是一种克服过拟合的方法。

4.2 使用解析解求解带有正则项的 loss 函数

4.2.1 求解最优解

在上一小节中我们得到添加数据量可以减少过拟合的发生，但是在实际中获取数据常常是一个费时费力的过程，于是我们为了减少过拟合的发生，添加一个正则项（即惩罚项），在本实验中经过一番尝试，在 λ =e-5 的时候可以获得较好的结果。我分别选取M=5，10，15，25，共让该模型跑4次，得到随着 M阶数的变化,每一次的结果如图4.7所示。

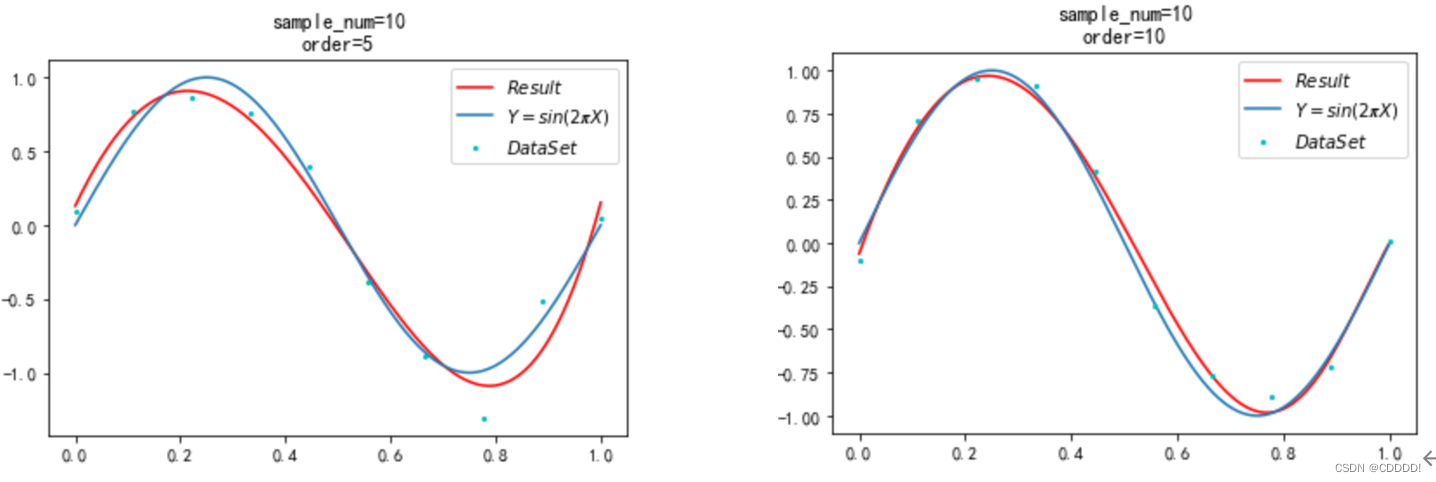
1. 5阶多项式                                                                 (b) 10阶多项式          

      

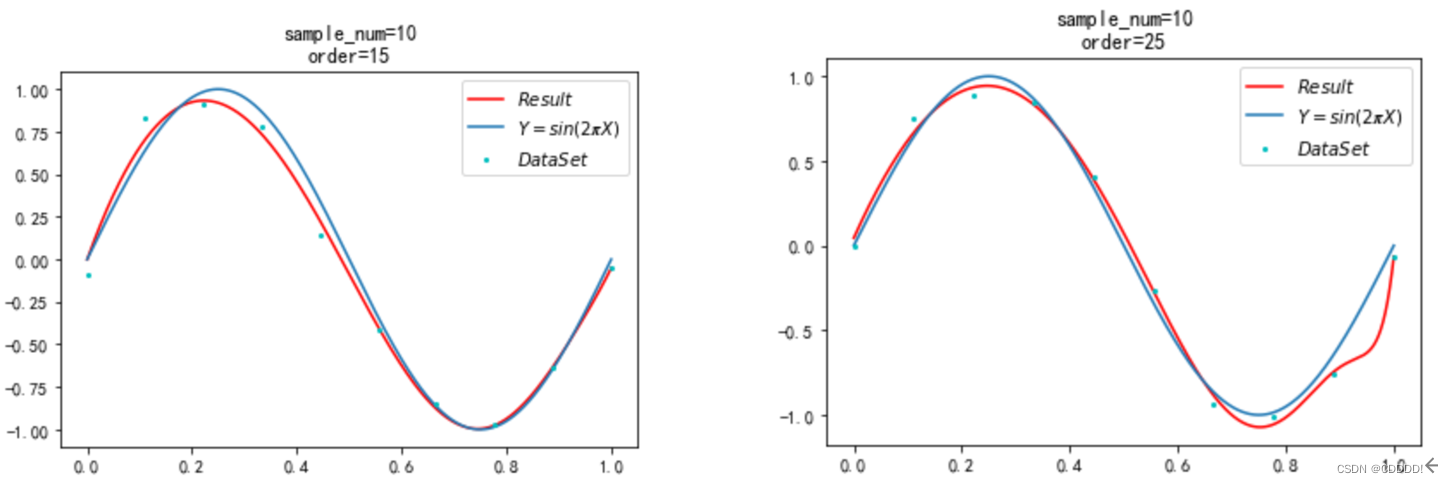
1.           15阶多项式                                                             (d) 25阶多项式

            图4.7 不同阶数多项式下的拟合效果

4.3 使用梯度下降法求解带有正则项的 loss 函数

4.3.1 求解最优解

经过一番尝试，我发现当步长设置在 0.1，λ 设置在 e-6 并且训练40万次的时候，可以得到如图4.8所示的较好结果，此时训练集上的 ERM S 是 0.03。

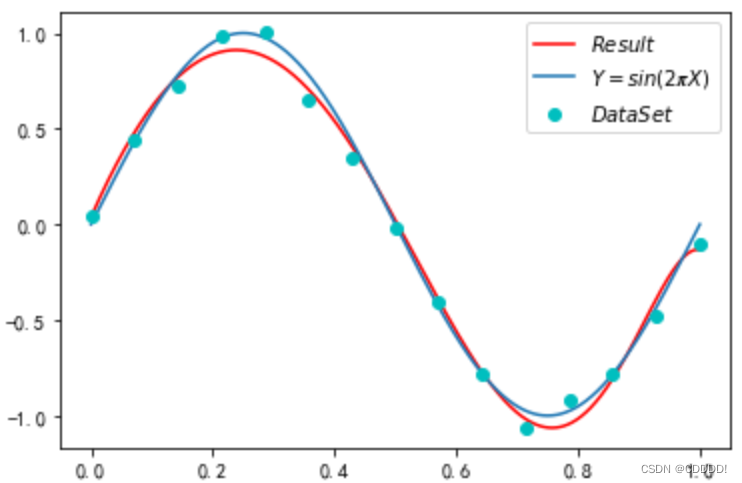
                图4.8  learning_rate=0.1,  λ=e-6

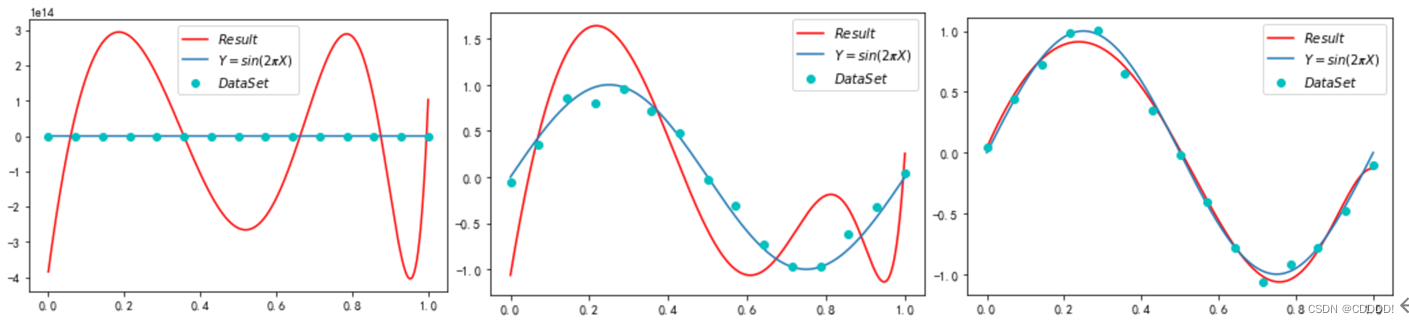
1.  λ=e-4                                               (b) λ=e-5                                      (c) λ=e-6

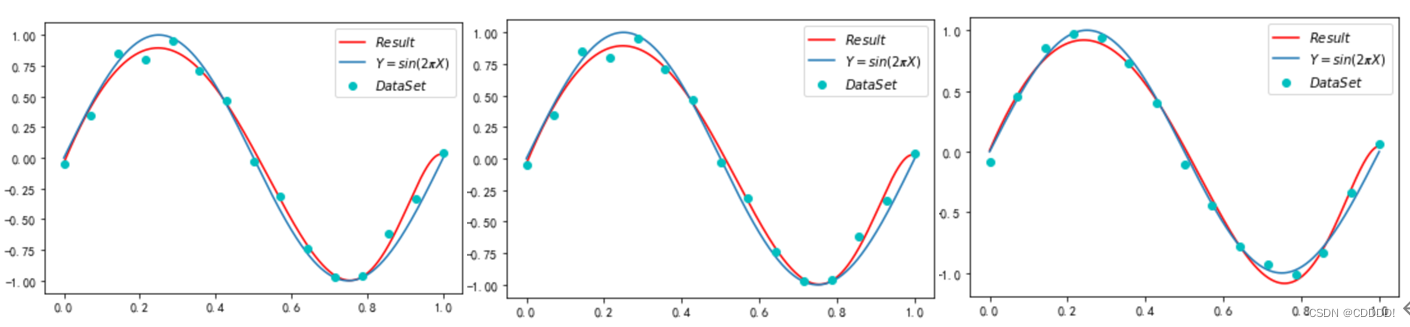
1.  λ=e-7                                                 (e)  λ=e-8                                   (f)  λ=e-9

图4.9 梯度下降法带有正则项的 loss 函数改变超参数模型的输出

经过多次尝试发现，当 λ<=e-6时，最终形成的结果效果都很好，且随着λ的减小，迭代达到对应精度的所需次数逐渐减小，最终可在20万次左右达到对应精度。

接下来，我修改了学习率(即步长)lr，分别取值1的-1到-6次方，得到不同情况下的拟合效果和loss曲线。(由于设备原因，迭代次数上限依旧为40万次）

            

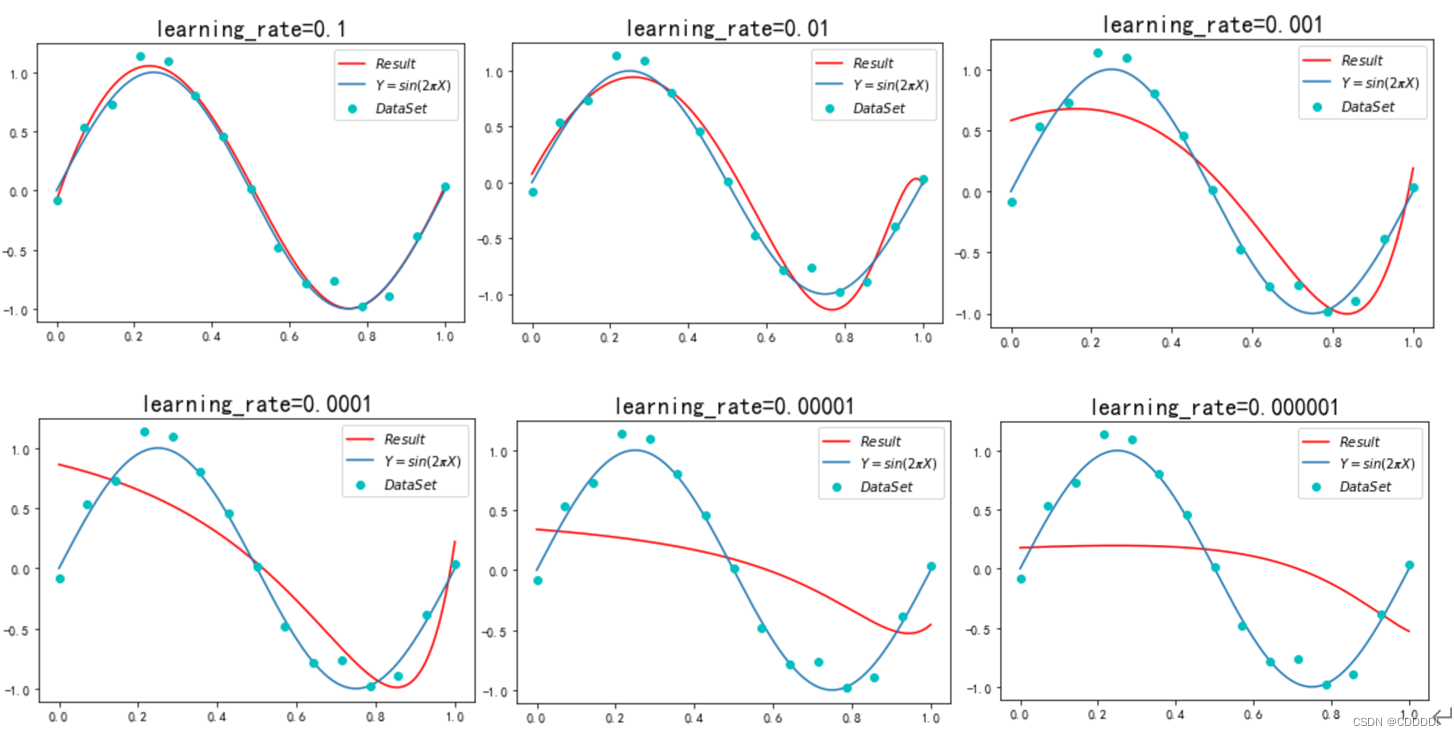
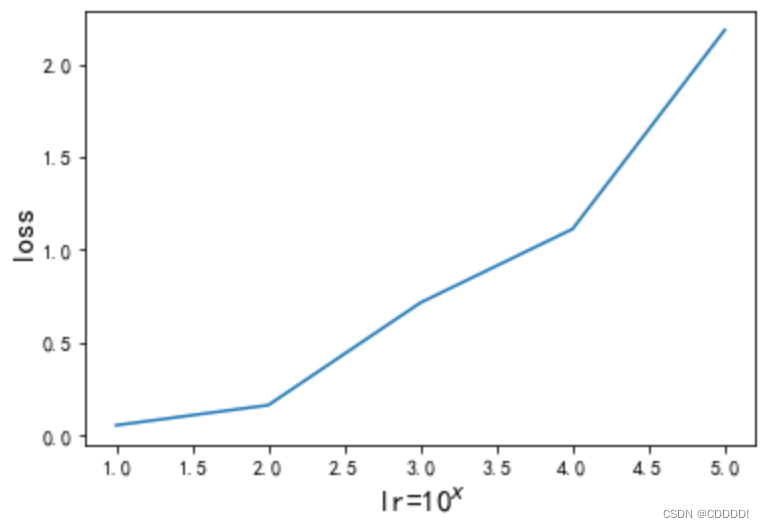
                       图4.11 不同lr下的loss曲线

  最后我尝试了在learning_rate=0.0000001时迭代400万次后的结果如图所示：

        

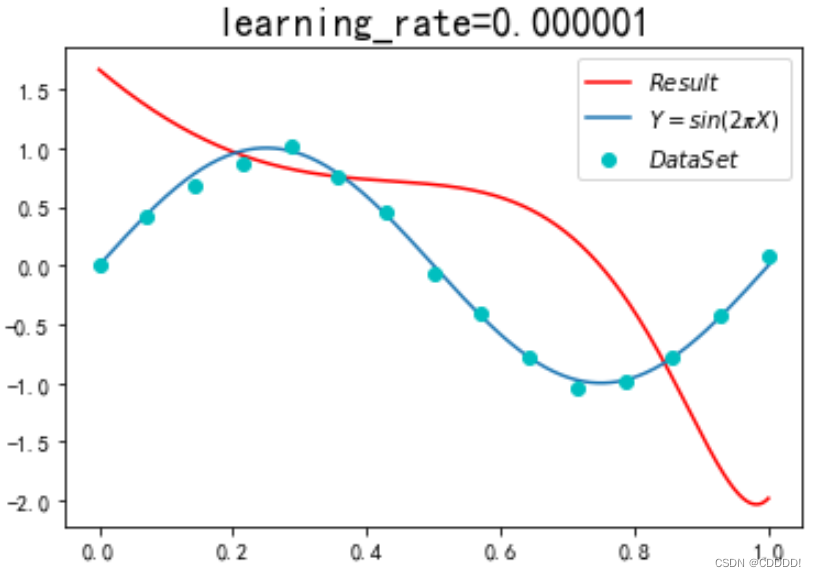
其效果表现出当学习率过低时，足够的迭代次数可能也无法弥补效果的差距。

4.5 共轭梯度法求解带有正则项的 loss 函数

4.5.1 求解最优解

本小节中，我们使用共轭梯度法求解带有正则项的 loss 函数，得到的结果4.12如图所示。其相较于共轭梯度法最大区别在于运行时间大大缩短。（受限于要求的函数较为简单，面对复杂函数时共轭梯度法能比梯度下降法效果更佳未能体现）。其损失函数为0.03。

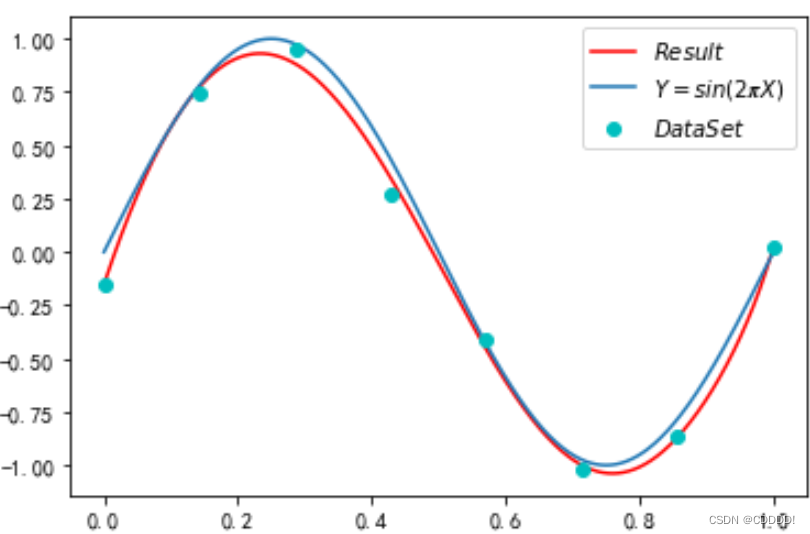
               图4.12 共轭梯度法拟合效果，sample=8

• 结论

在本文中，我们尝试了解析解、梯度下降、随机梯度下降、共轭梯度共四种方法，体会了不同的数据集大小，不同的超参数，不同的多项式阶数对机器学习模型的影响，熟悉了 python 语言中和矩阵运算的相关模块，加深了对于多项式回归这一机器学习基本模型的理解和实现能力。

• 参考文献

共轭梯度法英文维基百科 https://en.wikipedia.org/wiki/Conjugate_gradient_method
梯度下降法英文维基百科 https://en.wikipedia.org/wiki/Gradient_descent

斯坦福机器学习课程讲义吴恩达 http://www.andrewng.org

• 附录：源代码（带注释）

1. 最小二乘法(.ipynb)

1. import numpy as np  # 导入numpy库，此库用于进行矩阵运算等操作
2. import matplotlib.pyplot as plt  # 导入pyplot绘图库
3. plt.rcParams['font.sans-serif']=['SimHei']#显示中文
4. plt.rcParams['axes.unicode_minus']=False#显示负号
5. %matplotlib inlineglobal poly_degree # 多项式次数  
6. def funcy(X):  #定义初始函数
7.         return np.sin(2 * np.pi * X)
8. def getData(X_range, X_num, func, noise_variance):   #生成数据集
9.         X = np.linspace(X_range[0], X_range[1], num=sample_num)  # 生成对应范围和数量的等距向量
10.         Y = funcy(X) + np.random.normal(loc=0, scale=noise_variance, size=sample_num)
11.         # 生成X对应函数的值向量,增加了高斯噪声
12.         return X, Y
13. def get_matrix(x, M):   #生成(sample_num,order)的参数矩阵
14.         X = pow(x, 0)
15.         for i in range(1, M + 1):
16.                 X = np.column_stack((X, pow(x, i)))
17.         return X
18. def LeastSquareM(X, T):  # 最小二乘法求解向量
19.     s=X.size/sample_num
20.     regular = np.eye(int(s))
21.     regular[0][0] = 0
22.     lam=0.00001
23.     W = np.linalg.inv((X.T) @ X+lam*regular) @ (X.T) @ (T)  # lam=0时认无惩罚项
24.     return W
25. def loss(T, X, W):  #  定义对应损失函数
26.     Y = np.transpose(W) @ X.T  # 画出预测函数的值，X2·W得到的是一个样本数*1的向量
27.     a1 = Y.reshape(-1, 1).T @ X @ W
28.     a2 = Y.reshape(-1, 1).T @ T
29.     a31 = T.reshape(-1, 1).T @ X
30.     a32 = np.transpose(W).reshape(-1, 1)
31.     a3 = a31 @ a32
32.     a4 = T.reshape(-1, 1).T @ T.reshape(-1, 1)
33.     los = (a1 - a2 - a3 + a4).squeeze(-1).squeeze(-1)
34.     return los/sample_num
35. # 常量区
36. X_range = (0.0, 1.0)
37. sample_num = 10
38. funcName = funcy
39. noise_variance = 0.1  # 噪声的方差
40. level=26#多项式拟合阶数
41. # x, y为两个向量，对应的x[k],y[k]则是图像上的一个点\
42. x = np.linspace(0.0, 1.0, num=sample_num)  # 生成从0.0开始到2.0结束的sample_num个等距向量
43. y = funcy(x)  # 同样是一个数列，x的sin函数，注意numpy中默认使用弧度制
44. x2 = np.linspace(0.0, 1.0, num=1200)  #以此画出真值弧线和拟合弧线
45. y2 = funcy(x2)
47. errorList = list()  # 记录不同阶数的错误率List
48. _X, _Y = getData(X_range, sample_num, funcName, noise_variance)
49. # x 原始数据集的x坐标集合
50. # X 由x的1到n次方构成的矩阵
51. # W 求解的目标解向量
52. for i in range(1, level):
53.     X = get_matrix(x, i)
54.     W = LeastSquareM(X, _Y)  # W的计算使用样本的X
55.     errorList.append(loss(_Y, X, W))  # 计算这次循环的错误率，并加入到 errorList向量中
56. # value=X @ W
57. #plt.plot(x,value,"r-",x2,y2)
58. X2 = get_matrix(x2, level-1)  #画出拟合曲线所需的x坐标参数矩阵
59. value=X2 @ W  #得到拟合的y坐标
60. print("Value.shape:",value.shape)
61. plt.plot(x2,value.reshape(-1,1),"r-",x2,y2)
62. x1=np.linspace(0.0, 1.0, num=sample_num)
63. plt.plot(x1,_Y,"co",markersize=2.)
64. plt.legend(["$Result$","$Y=sin(2𝝅X)$","$DataSet$"])
65. plt.title("sample_num=10\norder=25")
66. plt.savefig(r"C:\\Users\\yuzezhao\\Desktop\\dataset\\"+str(sample_num)+"_"+str(level)+"level.png")
67. # 绘制不同M下的学习率
68. x_errorList = np.linspace(1, level, level-1)
69. plt.plot(x_errorList, errorList)
70. plt.grid()

1. 梯度下降法(.ipynb)(分开写的，请忽略序号）

1. import numpy as np  # 导入numpy库，此库用于进行矩阵运算等操作
2. import matplotlib.pyplot as plt  # 导入pyplot绘图库
3. import time
4. import math
5. plt.rcParams['font.sans-serif']=['SimHei']#显示中文
6. plt.rcParams['axes.unicode_minus']=False#显示负号
7. %matplotlib inline
8. def f1(x):
9.     return np.sin(2 * np.pi * x)
10. def getData(X_range, X_num, func, noise_variance):
11.     X = np.linspace(X_range[0], X_range[1], num=sample_num)  # 生成对应范围和数量的等距向量
12.     Y = func(X) + np.random.normal(loc=0, scale=noise_variance, size=sample_num)
13.     # 生成X对应函数的值向量,增加了高斯噪声
14.     print("_Y:", Y.size)
15.     return X, Y
16. def root_mean_square(X,W):  #计算损失函数
17. #     error = (X @ W - _Y.reshape(-1,1)) @(X @ W - _Y.reshape(-1,1))
18.     error=np.sum((X @ W - _Y.reshape(-1,1))**2)/2
19.     return error
20. def gradient_descent(X,lr, lam,level,errolist):
21.         #init value for __W
22.         start = time.time()
23. #         W = []
24. #         for i in range(level):
25. #             W.append(0)
26. #         W = np.array(W).reshape(-1, 1)
27.         W = 0.1*np.random.normal(size=(level,1),scale=1,loc=0)
28.         iteration_thresh = 4000000
29.         iter = 0
30.         thresh = 0.003
31.         while True:
32.             iter += 1
33.             term_vector = X @ W  - _Y.reshape(-1,1)
34.             W = W - lr / len(_X) *  X.transpose() @ term_vector + lam * W
35.             error_after = root_mean_square(X,W)
36.             if np.abs(error_after) <= thresh or iter == iteration_thresh:
37.                 print("iter:{0}\terror:{1}\n".format(iter, error_after))
38.                 errolist.append(error_after)
39.                 break
40.         end = time.time()
41.          print("Run time : {0}, with RMS : {1}".format(round((end-start), 2), round(error_after,2)))
42.          return round((end-start), 2) ,W
43. #------获得参数矩阵-----------------
44. def get_matrix(x, M):  # 获得参数矩阵X
45.         X = pow(x, 0)
46.         for i in range(1, M + 1):
47.                 X = np.column_stack((X, pow(x, i)))
48.         return X
49.         print("W.shape",W.shape)
50.         print("Run time : {0}, with RMS : {1}".format(round((end-start), 2), round(error_after,2)))
51.         return round((end-start), 2) ,W
52. # 常量赋值------------------------------------------------------------
53. X_range = (0.0, 1.0)
54. sample_num = 15
55. funcName = f1
56. level=15
57. noise_variance = 0.1  # 噪声的方差
58. # lam = np.exp(-18)
59. x1=np.linspace(0.0, 1.0, num=sample_num)
60. # x, y为两个向量，对应的x[k],y[k]则是图像上的一个点\
61. x = np.linspace(0.0, 1.0, num=sample_num)  # 生成从0.0开始到2.0结束的sample_num个等距向量
62. y = f1(x)  # 同样是一个数列，x的sin函数
63. x2 = np.linspace(0.0, 1.0, num=1200)  #以此画出真值弧线和拟合弧线
64. y2 = f1(x2)  #画出弧线
65. _X, _Y = getData(X_range, sample_num, funcName, noise_variance)
66. X = []
67. for i in _X:
68.     X.append([i ** j for j in range(0, level)])
69. X = np.array(X)  # X is the n * (m + 1) dimensional matrix
70. lr = 0.000001  #学习率
71. err=[]  #保存损失函数值
72. lam=1e-6  #正则项系数
73. #----测试不同学习率-------------------------------------------
74. # for lr1 in [0.1,0.01,0.001,0.0001,0.00001]:
75. #     theta,W=gradient_descent(X,lr1,lam,level,err)
76. # print('theta:', theta)
77. # err
78. #----计算theta和解向量W
79. theta,W=gradient_descent(X,lr,lam,level,err)
80. #----结果可视化
81. X2 = get_matrix(x2, level-1)
82. value=X2 @ W
83. x1=np.linspace(0.0, 1.0, num=sample_num)
84. plt.plot(x2,value,"r-",x2,y2)
85. plt.plot(x1,_Y,"co")
86. plt.legend(["$Result$","$Y=sin(2𝝅X)$","$DataSet$"])
87. plt.title("learning_rate=0.000001",size=18)

• 共轭梯度法(.ipynb)(请忽略序号)

1. import numpy as np  # 导入numpy库，此库用于进行矩阵运算等操作
2. import matplotlib.pyplot as plt  # 导入pyplot绘图库
3. import time
4. import math
5. plt.rcParams['font.sans-serif']=['SimHei']#显示中文
6. plt.rcParams['axes.unicode_minus']=False#显示负号
7. %matplotlib inline
8. def f1(x):
9.     return np.sin(2 * np.pi * x)
10. def getData(X_range, X_num, func, noise_variance):
11.     X = np.linspace(X_range[0], X_range[1], num=sample_num)  # 生成对应范围和数量的等距向量
12.     Y = func(X) + np.random.normal(loc=0, scale=noise_variance, size=sample_num)
13.     # 生成X对应函数的值向量,增加了高斯噪声
14.     print("_Y:", Y.size)
15.     return X, Y
16. #------共轭梯度法核心代码-----------------------------
17. def conjugate_gradient(Xcg,lam,level):
18.     /*
19.     # Xcg X的参数矩阵（sample_num,order)
20.     W = [0 for i in range(level)]
21.     W = np.array(W).reshape(-1, 1) # reshape to column vector
22.     y = _Y.reshape(-1, 1)
23.     print("Xcg.shape",Xcg.shape)
24.     y = Xcg.transpose() @ y
25.     print("y.shape",y.shape)
26.     X = Xcg.transpose() @ Xcg + lam * np.eye(Xcg.shape[1], Xcg.shape[1])
27.     r = y - X @ W # X为（sample_num,level)的阶数矩阵
28.     p = r
29.     print("r.shape",r.shape)
30.     rsold = r.transpose() @ r
31.     for i in range(len(_X)):
32.         Xp = X @ p
33.         print("Xp.shape:",Xp.shape)
34.         alpha = rsold / (p.transpose() @ Xp)
35.         W = W  + alpha * p
36.         r = r - alpha * Xp
37.         rsnew = r.transpose() @ r
38.         if rsnew < 1e-6:
39.             break
40.         else:
41.             p = r + rsnew/rsold * p
42.             rsold = rsnew
43.     return W
44. #------获得参数矩阵-----------------
45. def get_matrix(x, M):
46.         X = pow(x, 0)
47.         for i in range(1, M + 1):
48.                 X = np.column_stack((X, pow(x, i)))
49.         return X
50. #-------常量赋值-------------
51. X_range = (0.0, 1.0)
52. sample_num = 8
53. funcName = f1
54. level=15
55. noise_variance = 0.1  # 噪声的方差
56. # lam = np.exp(-18)
57. lam=0.01
58. x1=np.linspace(0.0, 1.0, num=sample_num)
59. # x, y为两个向量，对应的x[k],y[k]则是图像上的一个点\
60. x = np.linspace(0.0, 1.0, num=sample_num)  # 生成从0.0开始到2.0结束的50个等距向量
61. y = f1(x)  # 同样是一个数列，x的sin函数，注意numpy中默认使用弧度制
62. x2 = np.linspace(0.0, 1.0, num=1200)
63. y2 = f1(x2)
64. _X, _Y = getData(X_range, sample_num, funcName, noise_variance)
65. X = []
66. for i in _X:
67.     X.append([i ** j for j in range(0, level)])
68. X = np.array(X)  # X is the n * (m + 1) dimensional matrix
69. #----计算得到解向量
70. lr = 0.01
71. lam=1e-6
72. W=conjugate_gradient(X,lam,level)
73. #------结果可视化----------------------------
74. X2 = get_matrix(x2, level-1)
75. value=X2 @ W
76. x1=np.linspace(0.0, 1.0, num=sample_num)
77. plt.plot(x2,value,"r-",x2,y2)
78. plt.plot(x1,_Y,"co")
79. plt.legend(["$Result$","$Y=sin(2𝝅X)$","$DataSet$"])