机器学习实验（支持向量机SVM）

目录

一、支持向量机介绍

    1.1算法概述

    1.2算法原理

      1.2.1线性可分

      1.2.2寻找最大间隔

      1.2.3软间隔

      1.2.4低维到高维映射与核函数

   

     1.3算法优缺点

      1.3.1优点

      1.3.2缺点

二、支持向量机算法实践

     2.1加载数据集

     2.2SVM函数

     2.3绘制决策边界

     2.4测试

三、实验小结

---

一、支持向量机介绍

    1.1算法概述

       支持向量机（Support Vector Machine, SVM）是一种广泛应用的监督学习算法，主要用于数据分类问题。它基于统计学习理论和结构风险最小化原则，通过找到一个决策超平面来最大化不同类别之间的间隔，以此来实现数据分类。

    1.2算法原理

       SVM的工作原理其实并不复杂。首先，它尝试找到一个决策超平面（在二维空间中就是一条线，三维空间中是一个面，以此类推），将不同类别的数据点分隔开。但SVM并不满足于仅仅找到一个分隔面，它追求的是最优分隔面——即那个距离两边数据点都最远的分隔面。这个最优分隔面上的数据点，我们称之为“支持向量”，因为它们“支持”着这个分隔面，故它们对分类结果起着决定性的作用。

       SVM的一个核心思想是核技巧。简单来说，核技巧就是通过一个映射函数，将原始空间中的数据点映射到一个更高维的空间中，使得原本线性不可分的数据变得线性可分。

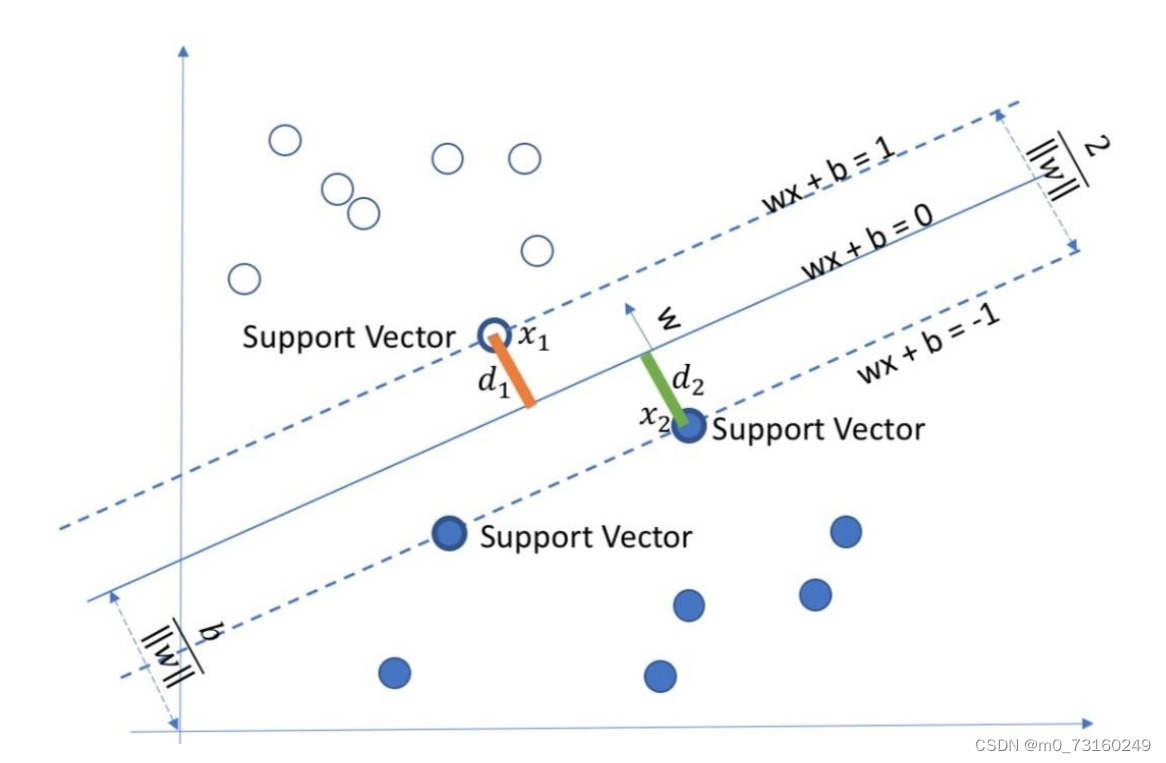
      1.2.1线性可分

       在二分类问题中，如果存在一个超平面能够将所有样本正确分类，则称这些样本是线性可分的。假设在n维空间中，超平面可以用以下方程表示：

       其中，w 是权重向量，x 是样本向量，b 是偏置项。对于线性可分的样本集，我们可以找到一个超平面，使得所有正类样本满足 ，负类样本满足。

      1.2.2寻找最大间隔

       SVM不仅要求找到一个超平面来划分样本，还要求这个超平面到两边的样本点的距离尽可能大，即寻找最大间隔。假设超平面到样本点 的距离为 ，则最大间隔可以表示为：

       通过推导，我们可以得到最大间隔的等价形式为：

      1.2.3软间隔

       在实际情况中，完全线性可分的样本集是很少的。SVM因为支持向量的选取的原因，很容易受噪声干扰，在现实中很容易因为部分样本导致支持向量间距过窄。为了处理那些不能被完全正确分类的样本，SVM引入了软间隔的概念。

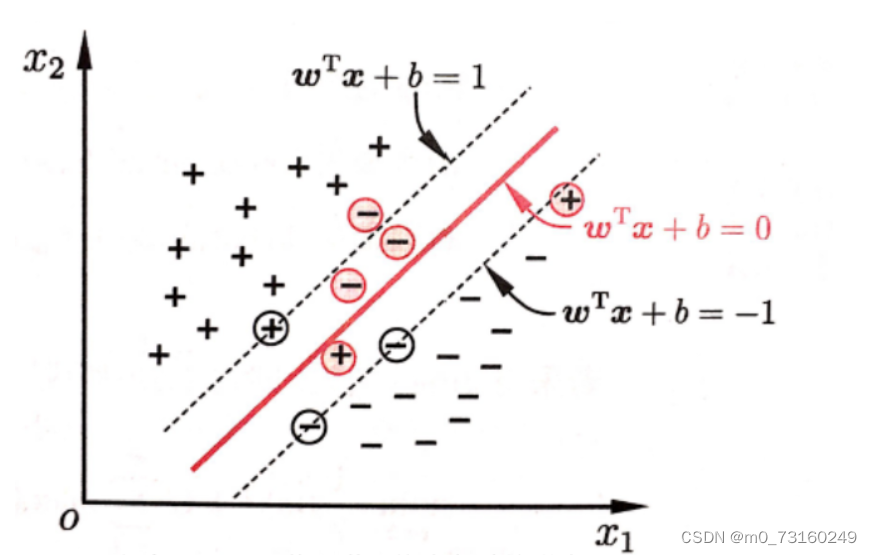
       这个时候我们引入软间隔，允许部分样本在间隔内。即允许一些样本点被错分到另一边，但同时要为这些样本点付出一定的代价。这可以通过引入松弛变量 ξi​ 来实现，此时的目标函数变为：

其中，C是一个常数，用于平衡间隔大小和错误分类的代价。

      1.2.4低维到高维映射与核函数

       当样本在原始空间线性不可分时，我们可以尝试将样本映射到一个更高维的空间中，使其变得线性可分。这可以通过使用一个非线性映射函数 ϕ(x) 来实现。在SVM中，我们通常使用核函数来隐式地实现这种映射。

       假设原始空间中的两个样本点为xi​和xj​，通过非线性映射ϕ将它们映射到高维空间，则高维空间中的点积可以表示为ϕ(xi​)⋅ϕ(xj​)。然而，直接计算ϕ(x)可能是困难的，因此SVM使用核函数K(xi​,xj​)来替代这个高维空间中的点积，即：

       通过选择合适的核函数，我们可以隐式地实现低维到高维的映射，并在高维空间中应用SVM算法。

几个常见核函数：

     1. 线性核（Linear Kernel）：

     线性核实际上不进行任何映射，直接在原始空间中计算点积。它适用于线性可分的情况。

     2. 多项式核（Polynomial Kernel）：

     多项式核可以实现非线性映射。

     3. 径向基函数（RBF）核（Radial Basis Function Kernel）：

     RBF核也称为高斯核，是一种常用的核函数，它可以将样本映射到一个无穷维的空间中。

     4. Sigmoid核（Sigmoid Kernel）：

   

     1.3算法优缺点

      1.3.1优点

1. 高效性：SVM在处理高维数据时表现出色，因为它只关注支持向量，而忽略大部分非支持向量。
2. 泛化能力强：由于SVM追求的是最优分隔面，因此它对新数据的分类能力通常很强。
3. 鲁棒性：SVM对噪声和异常值有一定的容忍度，不会因为个别数据点的偏离而影响整体分类效果。

      1.3.2缺点

1. 计算复杂性：当数据量非常大时，SVM的训练时间会显著增加，因为需要计算每个数据点到分隔面的距离。
2. 参数选择：SVM的性能受到参数选择的影响，如核函数的选择、惩罚系数C等。这些参数通常需要通过交叉验证等方法进行调优。

二、支持向量机算法实践

     2.1加载数据集

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
df = {
    '颜色深度':[14.23,13.2,13.16,14.37,13.24,12.07,12.43,11.79,12.37,12.04,10.65,13.42,11.2,14.33,13.2,12.8,11.6,12.43,12.55,13.2,12.85],
    '酒精浓度':[5.64,4.38,5.68,4.80,4.32,2.76,3.94,3.0,2.12,2.6,3.22,5.0,4,4,5.7,3.8,4.2,4.6,3.1,3.4,4.3],
    '品种':[0,0,0,0,0,1,1,1,1,1,1,0,1,0,0,0,1,0,1,1,0]} 
 
 
wine_data = pd.DataFrame(df)
X = np.array(wine_data.iloc[:,:2])  #特征（颜色深度/酒精浓度）
y = np.array(wine_data.iloc[:,-1])  #标签 （品种：0黑皮诺，1赤霞珠)
 
#用Matplotlib创建散点图
plt.rcParams['font.sans-serif'] = 'SimHei' #设置中文显示，mac系统
plt.rcParams['axes.unicode_minus'] = False
 
plt.style.use('ggplot')
plt.figure(figsize = (9,6),dpi=200)
 
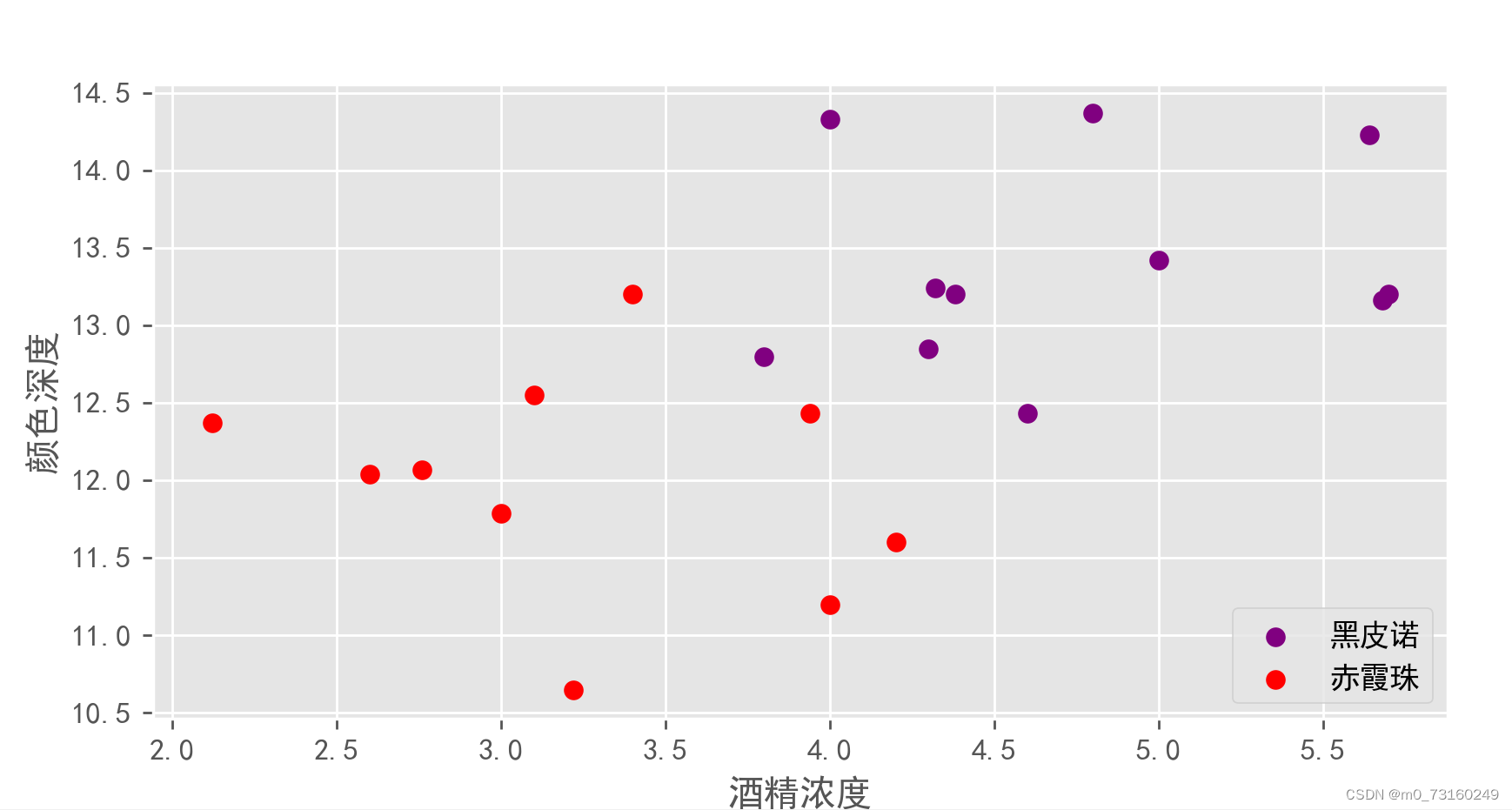
plt.scatter(X[y==0,1],X[y==0,0],color = 'purple',label = '黑皮诺')
plt.scatter(X[y==1,1],X[y==1,0],color = 'red',label = '赤霞珠')
 
plt.xlabel('酒精浓度')
plt.ylabel('颜色深度')
plt.legend(loc='lower right')
plt.show()

       输出：

     2.2SVM函数

# 添加偏置项（b）到X中  
m, n = X.shape  
X = np.hstack((np.ones((m, 1)), X))  
  
# SVM参数  
C = 1.23  # 惩罚系数  
learning_rate = 0.01  # 学习率  
epochs = 2000  # 迭代次数  
  
# 初始化权重和偏置  
w = np.zeros(n + 1)  
b = 0  
  
# 梯度下降法  
for epoch in range(epochs):  
    # 计算预测值  
    y_pred = np.sign(np.dot(X, w) + b)  
      
    # 计算损失函数的梯度（这里使用hinge loss的次梯度）  
    gradients = np.zeros(n + 1)  
    for i in range(m):  
        if y[i] * (np.dot(X[i], w) + b) < 1:  
            gradients += C * y[i] * X[i]  
        else:  
            gradients += 0  
    gradients /= m  
      
    # 更新权重
    w -= learning_rate * gradients  


#支持向量更新偏置b
def update_bias_with_support_vectors(X, y, w, b, support_vectors_indices=None):  
    
    if support_vectors_indices is None:  
        # 计算预测值（注意这里不需要加b，因为X已经包含了偏置项）  
        unsigned_predictions = np.dot(X[:, :-1], w[:-1]) + w[-1]  # 假设X的最后一列是偏置项，w的最后一个元素是b  
        # 找到支持向量的索引  
        support_vectors_indices = np.where(y * unsigned_predictions <= 1)[0]  
      
    # 使用支持向量来更新偏置项b  
    b_numerator = 0  
    b_denominator = 0  
    for i in support_vectors_indices:  
        # 确保该点确实是一个支持向量（即位于边界上或内部）  
        if y[i] * (np.dot(X[i, :-1], w[:-1]) + w[-1]) <= 1:  
            b_numerator += y[i]  
            b_denominator += 1  
      
    # 计算新的偏置项b  
    if b_denominator > 0:  
        b_new = -np.dot(w[:-1], X[support_vectors_indices[0], :-1].T) + 1 / b_denominator * b_numerator  
    else:    
        b_new = b  
      
    return b_new 

# 最终的分类函数  
def classify(x):  
    return np.sign(np.dot(x, w) + b_new)

    x: numpy数组，形状为(m, n+1)，其中m是样本数量，n是特征数量，最后一列是偏置项（通常为1）。  
    y: numpy数组，形状为(m,)，包含样本的标签。  
    w: numpy数组，形状为(n+1,)，包含权重和偏置项（如果w是通过不包括偏置项的特征矩阵训练得到的，则需要额外处理）。  
    b: 浮点数，当前的偏置项值。  
    support_vectors_indices: numpy数组或None，包含支持向量索引的数组。如果为None，则自动计算。  
    返回:  
    b_new: 更新后的偏置项值。  

       输出：

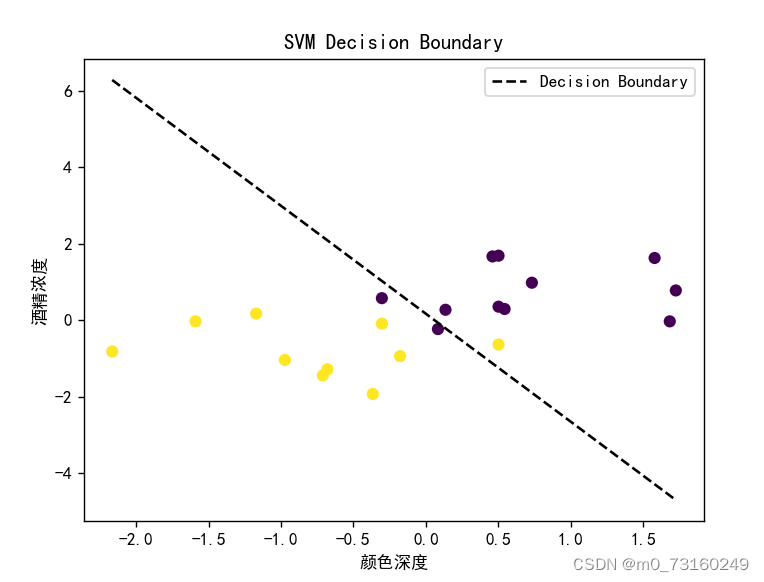
     2.3绘制决策边界

# 绘制数据点和决策边界  
def plot_data_and_boundary(X, y, w, b):  
    # 绘制数据点  
    plt.scatter(X[:, 1], X[:, 2], c=y, cmap='viridis', marker='o')  
      
    # 计算决策边界的斜率和截距  
    slope = -w[1] / w[2]  # 斜率，这里w[0]是偏置项的系数，通常为1  
    intercept = -b / w[2]  # 截距  
      
    # 生成决策边界线的x值范围  
    x_boundary = np.linspace(X[:, 1].min(), X[:, 1].max(), 100)  
    y_boundary = slope * x_boundary + intercept  # 根据斜率和截距计算y值  
      
    # 绘制决策边界线  
    plt.plot(x_boundary, y_boundary, 'k--', label='Decision Boundary')  
    
    #用Matplotlib创建散点图
    plt.rcParams['font.sans-serif'] = 'SimHei' #设置中文显示
    plt.rcParams['axes.unicode_minus'] = False

    # 显示图例和坐标轴标签  
    plt.legend()  
    plt.xlabel('颜色深度')  
    plt.ylabel('酒精浓度')  
    plt.title('SVM Decision Boundary')  
    plt.show()

       输出：

     2.4测试

# 数据标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 调用绘图函数  
plot_data_and_boundary(X_scaled, y, w, b)
# 示例：预测一个新的数据点  
new_point = np.array([1, 13.5, 4.5])  # 假设这是一个新的数据点，包含偏置项  
k=classify(new_point)
print(classify(new_point))  # 输出预测结果，-1或1
if k==1:
   print("品种为黑皮诺")
else:
   print("品种为赤霞珠")

       输出：

三、实验小结

       在支持向量机（SVM）实验中，我们深入了解了SVM的基本原理和参数调整的重要性。通过调整惩罚系数C，我们观察到了模型在训练集和测试集上的性能变化。实验表明，选择一个合适的C值对于防止过拟合和确保模型泛化能力至关重要。此外，我们还探索了通过支持向量来更新偏置项b的方法，这进一步加深了对SVM内部机制的理解。