导数应用

知识点

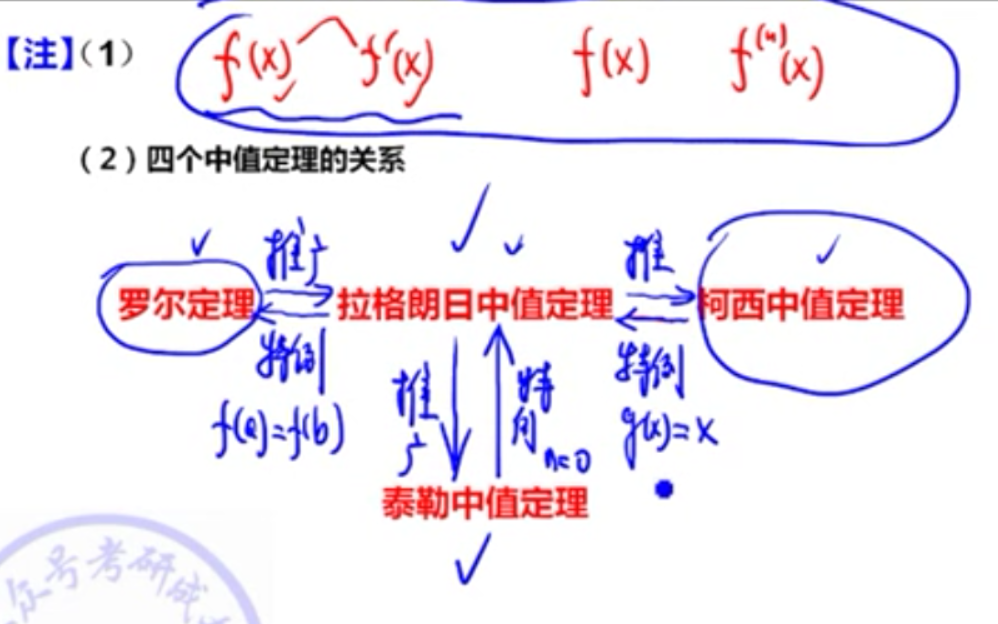
• 构建了函数与导数的关系，特例与推广之间的关系

• 注意极值的定义
• 若函数可导，则极值点→驻点
• 若函数不一定可导，则极值点与驻点无关系
• 只有导数为0的点和不可导点才是可能的极值点

• 第三充分条件可通过，皮亚诺余项泰勒公式和极值定义证明

• 凸凹性就是切线与弦的关系

• 二阶导数变号

• 二阶导为0且三阶导不为0，或者奇数阶导为0（类比极值点第三充分条件），或者二阶不可导的点

---

题型

• 偶函数

• 隐函数求二阶导时，注意一阶导在该点若为0，那么一阶导为系数的项，则不用完全求导，其他提前得了0的项也类似，具体见李正元例4.15及其后面的评注

• 举例法
• 注意本题是二阶连续导，所以二阶导为0，但是去心邻域内大于0

• 二阶导连续

• 经典错误，有二阶导，没说二阶导是否连续，只能用一次洛必达

• 利用保号性，分别讨论$a>0$, $a<0$的情况，确定$f(x_0+h)$ $f(x_0)$在邻域内的大小关系，根据极值定义即可得出结果

• $f^{\prime \prime }(x)=sinx-[f^{\prime }(x){]}^2$，可导-可导=可导，所以$f(x)$三阶可导
• n为奇数，导数不为0是拐点，偶数不为0是极值点

• 注意$t$与$x$的关系，然后再通过$t$的范围来确定$x$的范围

• 求极限的功夫要过关

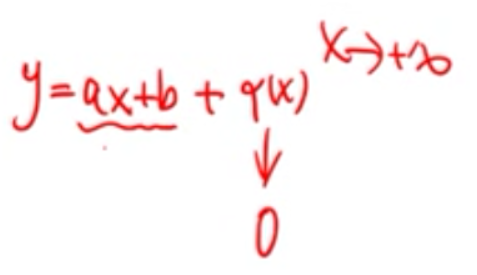
• 斜渐近线另一种求法，把原函数改写成$y=ax+b+\alpha (x)$，（$x\to +\infty$时，$\alpha (x)\to 0$），则$y=ax+b$就是斜渐近线

• 用一步泰勒公式

• 注意$e$的无穷次方要分正负！！！

• 偶函数，对称美！所以渐近线也是对称的
• $arctanx$的无穷次方也要注意正负！！！

• $arctanx+arctan\frac{1}{x}=\frac{\pi }{2}$

• 罗尔定理推论，直接用

假设有$n+1$个零点，则反复使用罗尔定理可得出，$n$阶导数有一个0点，与条件矛盾

• 零点定理：①连续②异号
• 罗尔定理：要找个原函数（闭区间连续，开区间可导，端点值相等）

• 罗尔定理

• 对数比幂函数趋近0的速度快（见李正元例1.37）

• $[0,1]$区间$t^2$比$t$小

• 注意找好判定正负的点

• 罗尔定理推论

• 根据极值的定义，端点不可能是极值点！

• 罗尔定理推论
• 用反证法也可，假设还有个零点，则两个零点之间存在导数为0的点，与条件矛盾

• 用拉格朗日余项的泰勒公式证有一个点的值小于0（在题目给出信息最多的点展开）

• 拉格朗日中值定理

• 李正元例4.23

• 泰勒公式
• 拉格朗日
• 唯一极值点就是最值点

• 凹凸性，切线与割线的关系

• 凹凸性

---

罗尔定理

• $a,b$同号所以$\xi$不可能是0

• 可用拉格朗日或者罗尔定理

• $\xi f^{\prime }(\xi )+nf(\xi )=0$，令$F(x)=x^{n}f(x)$

• 利用积分中值定理再找个零点

• 第一步的分段构造函数方法类似李正元例4.34
• $\xi f^{\prime }(\xi )-nf(\xi )=0$，令$F(x)=\frac{f(x)}{x^n}$

• 方法+规律

---

拉格朗日中值定理、柯西中值定理

• 注意第一问的结论

• 根据逆推法分析出分界点，且保证分界点是存在的
• 互不相同很重要！！！相同就变成简单题了

---

泰勒中值定理

• 套个绝对值，取两个$f^{\prime \prime }(\xi )$中大的那个，放大一次，
  ∣ f ( b ) − f ( a ) ∣ < = ( b − a ) 2 8 ( ∣ f ′ ′ ( ξ 1 ) ∣ + ∣ f ′ ′ ( ξ 2 ) ∣ < = 2 m a x { f ′ ′ ( ξ 1 ) , f ′ ′ ( ξ 2 ) } |f(b)-f(a)|<=\frac{(b-a)^{2}}{8}(|f''(\xi_1)|+|f''(\xi_2)|<=2max\{f''(\xi_1),f''(\xi_2)\} ∣f(b)−f(a)∣<=8(b−a)2​(∣f′′(ξ1​)∣+∣f′′(ξ2​)∣<=2max{f′′(ξ1​),f′′(ξ2​)}

• 提供信息一样多，就选有导数值的那个点