第二章 一元函数的导数与微分概念及其计算

第二章 一元函数的导数与微分概念及其计算

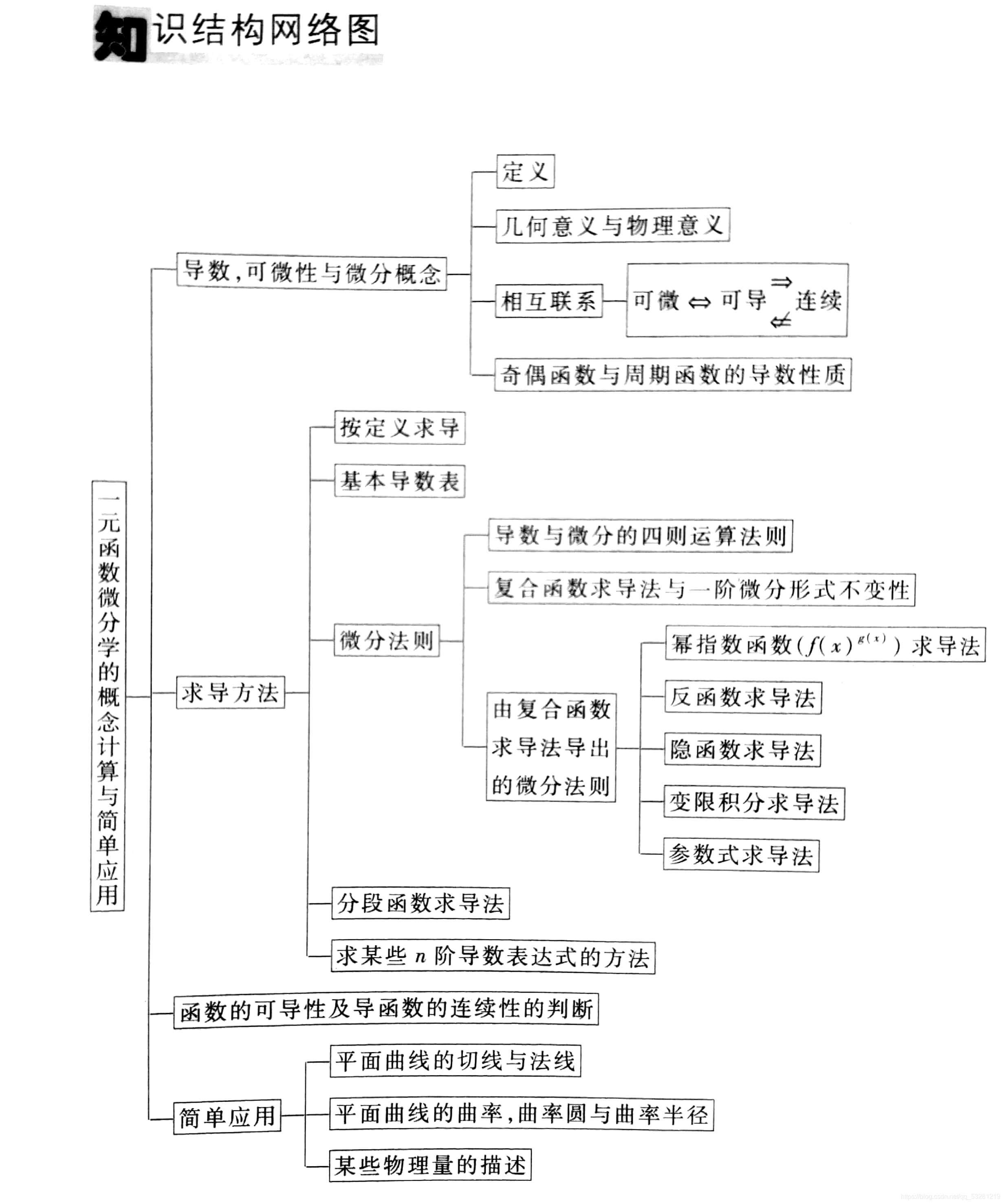
一、一元函数的导数与微分

（一）导数的定义、几何意义与力学意义

1. 导数的定义
   2.1 定义
   2.2 左右导数
2. 几何意义（切线斜率）
3. 力学意义（物理的速度）

（二）单侧可导与双侧可导的关系

2.1 可导的充要条件，左右导数存在且相等

（三）可微的定义、微分的几何意义及可微、可导与连续之间的关系

1. 可微的定义
2. 微分的几何意义
   Δy是f(x)的增量，dy是切线的增量
3. 可导、可微与连续之间的关系
   可微与可导等价

（四）函数在区间上的可导性，导函数及高阶导数

1. 函数在区间上的可导性
2. 导函数
3. 二阶导数及高阶导数
4. 二阶导数的力学意义（物理的加速度）

（五）奇偶函数与周期函数的导数性质

奇的导数为偶，偶的导数为奇
周期函数的导数也是周期函数且周期相同

---

二、按定义求导数及其适用的情形

（一）按定义求导数

注意，Δx→0时，若f(x + Δx) - f(x)不是无穷小量则f '(x0)不存在

（二）适合用定义求导数的几种情形

分段函数
只说连续没说可导

（三）利用导数的定义求极限

Ⅰ 直接按导数的定义求，注意增量的替换，只要趋近于0即可替换

Ⅱ 数列极限与导数的关系

---

三、基本初等函数导数表，导数四则运算法则与复合函数微分法则

（一）基本初等函数导数表（微分表）

（二）导数与微分的四则运算法则

（三）复合函数的微分