强化学习的数学原理：时序差分算法

概述

之前第五次课时学习的 蒙特卡洛 的方法是全课程当中第一次介绍的第一种 model-free 的方法，而本次课的 Temporal-Difference Learning 简称 TD learning （时序差分算法）就是第二种 model-free 的方法。而对于 蒙特卡洛方法其是一种 non-incremental 的方法，而 TD 则是一种 incremental 的方法。

另外下一节课讲 Value Function Approximation 值函数近似 这一节时，也是基于本节课要讲的 TD 方法，只不过本节课的 TD 方法是基于 table 的，即 tabular representation（表格表示法）。而下一节课的则是基于 function 的 representation。

非常经典的 Deep Q learning 也会在下一节课中介绍。

本节课大纲如下：

Motivating examples

在这一部分我们会考虑几个例子，然后使用上节课中的 RM 算法来进行求解，这是为了建立上节课和这节课之间的关系，这样就不会在学习 TD 算法的时候觉得唐突了。我们就会明白为什么 TD 算法是长这个样子。

首先要提到的还是 mean estimation 的问题，对于 mean estimation 这个问题，就是要求解一个 random variable X 它的 expectation，然后用 w 来表示这样一个 expectation 的值，然后已经有的是这个 X 的一些采样，我们使用这些采样来求解这个 expectation 。求解的算法有很多，这里专门使用 RM 算法来进行一下求解。

这个其实在上一节课已经讲过很多遍了，下面简单的回顾下：

下面来看第二个例子，这个例子要比上面那个更加复杂一些，因为这里 w = E[V(X)] ；为了解决这个问题，思路其实和上面的例子是一样的：

再来看最后一个例子，现在是有两个随机变量 R 和 X 了，并且表达式也更复杂了些，那么这个时候如何求解这个 expectation 呢？思路还是一样的：

最后得到的这个式子：

实际上一会儿在看到 TD 算法的表达式的时候，会发现和这个表达式已经非常的相像了。

小结一下：

TD learning of state values

接下来我们正式介绍第一种 TD 算法，对于 TD 算法我们首先要明确它是在干嘛，它是在求解一个给定的策略 Π 的 state value，为什么要求解这个 state value 呢？是因为求解出来之后我们就做了 policy evaluation，那么之后和 policy improvement 相结合，我们就可以去找最优的策略了。

首先要注意的是，TD 算法其实既可以指一大类的这样一个算法，像本节课讲的所有算法都属于 TD 算法，包括 Q-learning，但是我们接下来要讲的这个 TD 算法是最经典最原始的一种 TD 算法，其就是用来估计 state value 的，有一个非常明确的表达式，所以这个时候的 TD 算法指的是一个特定的算法，要注意区分。

介绍的方法很简单，就是直接给出该算法，然后再慢慢进行分析：

TD 算法是基于数据也就是不基于模型来实现强化学习的，那它要的数据是什么呢？就是上图中的这一部分：

可以称为数据也可以称为 experience，可以写成上面蓝色部分的两种形式中的任意一种。

而 TD 算法就是要使用这些数据来估计这个 Π 所对应的 state value：

在上图的 TD 算法式子中，有符号 v(s)，这个 s 表示的就是 state space 当中的任何一个状态。也就是 state space 当中任何一个状态我都要有一个 v，然后这个 v 是来近似 vΠ(s) 也就是 s 的 state value 。

另外这个 v 在 t 时刻会有一个下标 t ，这个代表是在 t 时刻的一个估计值。因此 t + 1 时刻那就是 t+1 时刻的估计值，它是在不断变化的。

在这个式子中还有一个 st，st 是什么呢？就是在一个 episode 里面或者说这样一个经验里面，我在 t 时刻所访问到的那个状态就是 st 。因为一个 agent 在环境当中它一个时刻只能访问一个状态。

那么这个算法究竟是在干嘛呢？它实际上包括两部分。

可以看见上图中 TD 算法有两个式子，其中第一个表达式后面会说，先看第二个表达式，第二个式子的意思是在 t 时刻的时候不是已经访问了 st 了吗？那么所有其它的状态都没有被访问，那所有没被访问的话它的 v 是保持不动的，所以 V(t+1)(s) = V(t)。实际上平时在其它地方看到 TD 算法的时候是看不到第二个式子的，因为第二个式子是隐含掉了。

那么接下来仔细分析一下第一个式子：

分析上面式子：首先左边是 v(t+1) 它是对 st 的 v state value 的一个新的估计，这个新的估计是由什么得到呢？是由等式右边的两项得到的。第一项是这个 current estimate 一个旧的估计，然后加上了一个修正项，修正项里面的 αt是针对 st 的一个系数，然后中括号里面它们有几个名字，需要分别介绍一下。

首先第一个是 r(t+1) + γvt(s(t+1))，它有一个名字称为 TD target。为什么叫 TD target 这个后面会介绍，实际上它就是希望这个 vt 能够朝着这个 target 的方向去修改，也就是能够更加的去接近这个 target。

然后现在的这个 value 和这个 target 之间存在一个误差，这个误差就被称为 TD error，怎么样来理解这个 TD error 呢？这个也放在后面介绍。

总而言之新的 estimate 是由旧的 estimate 然后再加上一个修正项所得到的。

接下来我们分析 TD target 和 TD error 该怎么理解。理解这两部分对于深刻理解 TD 算法具有非常重要的作用，一定要仔细学习：

首先第一个问题，我们为什么把 vt bar 叫作 TD target？原因很简单，这个算法所做的事情很简单它就是要把 v(st) 朝着 vt bar 的这个方向去改进，也就是到下个时刻 v(st) 离 vt bar 会更加的接近，所以 vt bar 是它的一个目标值，所以为什么它叫做 TD target 。

来看一下为什么是这样的：

在上图中的推导过程中，在这一步：

得到如上图的式子，这个方程描述了什么呢？它描述了 vt 和 vt bar 它们之间的差的变化。vt(st) - vt bar 这是在 t 时刻的，而等式左边的 v(t+1)(st) - vt bar 是在 t+1 时刻的。一会儿我们将说明这个 v(t+1) 实际上离 vt bar 会更近。为什么呢？就是继续往下推导呗，推导过程在上上图中已经推完了的：

接下来来看一下怎么理解 TD error：

从上图中不难得知，TD error 包含了两个量，一个是 v(st) 这是在 t 时刻，而另一个 r(t+1)+γv(s(t+1)) 是在 t+1 时刻，所以这也就是为什么TD算法被称为 Temporal Difference Learning 时序差分算法的原因。为什么是时序？因为是在两个时刻，这个是比较直观的理解。

然后这个 TD error 不仅仅描述了这两个时间量之间的误差，它更描述了什么呢？vt 和 vΠ 之间的误差。vΠ 是我们要估计的值，vt 是我们当前估计的值，一句话概括：当 vt 等于 vΠ 的时候 δt 应该等于 0，那反过来δt 不等于0 那就说明了 vt 不等于 vΠ 。

最后 TD error 的一个理解就是它是一种 innovation，什么是 innovation？就是新的信息，就是当前时刻我对 vΠ 有一个估计，但这个估计可能是不准确的，然后我来了一个新的 experience，然后把这个 experience 和我的估计联系到一起就计算出来了这个 error，我就发现了为什么会有一个 error 存在。这个 error 的存在就说明了我当前的估计是不准确的。因此我们使用这个 error 来改进我当前的这个估计。所以这个是一种新的有用的信息。

下面是 TD 算法的一些基本的性质：

TD 算法究竟在干一个什么事情呢？它实际上就是我要给定一个策略，然后我要估计出它的 state value，所以我们刚才介绍的这个 TD 算法它只是来估计 state value，只是来做 policy evaluation 这个事情，那么它不能做什么呢？它不能来估计 action value，它也不能直接搜索到最优的策略。

但是在这个基础之上，我们马上会介绍一系列的 TD 算法，然后它们能够来估计 action value，并且和 policy improvement 的这一个步骤相结合，就能够来搜索最优的策略。

因此刚才所介绍的这个 TD 算法虽然非常简单，但是它是后面一系列算法的基础。

TD learning of state values - The idea of the algorithm

最后再从数学上来看一下 TD 算法到底在干什么以及为什么它会长成这个样子：

其实就是为了解决在没有模型的情况下求解一个给定策略 Π 的贝尔曼公式。

接下来就是一些数学证明：

TD learning of action values：Sarsa

Sarsa 及其变形算法它们在做什么事情呢？就是我给定义一个策略我能够估计出来 action value，所以它们能够做 policy evaluation。然后再结合 policy improvement 那么就可以找到最优的策略，而 Q-learning 在做什么呢？它则是直接来求解这个 optimal action value，从而就可以直接找到最优的策略。

接下来我们来看 Sarsa 算法：

在上一小节当中我们介绍的 TD 算法是用来估计一个给定策略的 state value。我们知道在我们要去改进策略的时候我们是需要估计出 action value 的，这样哪一个 action value 大我们就选择哪一个作为新的策略。而上一节中的 TD 算法显然不能估计 action value，因此我们使用到 Sarsa 算法来完成这个事情。

等一下就会看到 Sarsa 和这个我们刚才介绍的基础 TD 算法是非常类似的形式。

Sarsa 估计出来 action value 之后其实际上在做的也就是 policy evaluation，就是你给我一个策略我怎么把策略的 action value 给估计出来，但这个还是不能找到最优的策略，而强化学习的目的是要找到最优的策略，怎么办？可以把 Sarsa policy evaluation 这个算法和 policy improvement 那个算法相结合起来，这样就可以找到最优的策略。

接下来我们介绍两部分，第一部分我们先来看如果你给我一个策略我怎么样去把它的 action value 给估计出来：

我们没有模型所以我们要有数据或者说我们要有 experience，假设我们有这样的 experience 这是一个集合：

然后这个集合有很多个不同时刻的 t，然后每一个时刻所对应的 experience 是 st、at、r(t+1)、s(t+1) 和 at+1 。

有了这些数据之后我们怎么做呢？我们就可以使用这个 Sarsa 算法来进行更新了：

在上图这个算法中，q(s, a) 是 qΠ(s, a) 的一个估计值，那如果是 qt 的话就是在 t 时刻它的估计值。

可以看到这和我们刚才所说的 TD 算法是很相像的，不过是把 v(st) 换成了 q(st, at) 而已。

那为什么这个算法叫 Sarsa 呢？原因很简单：它是 state、action、reward、state、action 这五个单词的首字母的缩写：

Sarsa 在解决一个什么样的数学问题呢？Sarsa 实际上也是求解了一个贝尔曼公式，只不过这个贝尔曼公式的形式有所不同，是什么呢：

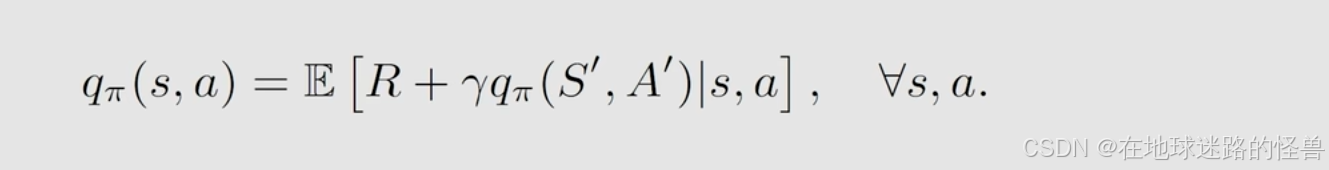
和之前我们所看到的所有贝尔曼公式不同的地方在于它是使用 action value 来表达的，而不是基于 state value 来表达的。所以这个贝尔曼公式刻画了不同 action value 之间的关系，但是实际上都是一样的，所以它也是贝尔曼公式。

它的收敛性和之前所说的基础的 TD 算法的定义是一模一样的：

不管怎样这个定理告诉我们只是 qt 收敛到了 qΠ ，所以还是我要给定一个策略然后我估计出来它的 action value，所以下面为了要得到最优的 policy 我们还需要把这个过程和一个 policy improvement 相结合才可以。

实际上结合之后的算法也被称为 Sarsa，或者说在大多数情况下其实大家听到 Sarsa 的时候实际上是把 policy evaluation 和 policy improvement 这两个结合之后的算法。

下面就是将 Sarsa 和 policy improvement 结合起来实现的伪代码：

Sarsa Implementation

import random

import numpy as np
import time
import os

from matplotlib import pyplot as plt


def get_reward(location, action, graph):
    # r, c 表示地图的行数和列数
    r, c = len(graph), len(graph[0])
    reward = -1  # 默认奖励为 -1，因为要求走最短路径
    # row, col 表示当前所在行列位置
    row, col = location
    # 采取行动为0，表示往上，那么当前位置的行数+1
    if action == 0:
        row = row - 1
    # 采取行动为1，表示往下，那么当前位置的行数-1
    elif action == 1:
        row = row + 1
    # 采取行动为2，表示往左，那么当前位置的列数-1
    elif action == 2:
        col = col - 1
    # 采取行动为3，表示往右，那么当前位置的列数+1
    elif action == 3:
        col = col + 1

    # 如果采取了action后的所在行列位置越界了，reward-1
    if row < 0 or row > r - 1 or col < 0 or col > c - 1:
        reward = -1
    # 如果采取了action后的所在行列位置在forbidden area，reward-100
    # 这表示我们并不想让 agent 走进 forbidden area
    elif graph[row][col] == '×':
        reward = -100
    # 如果采取了action后的所在行列位置在目标位置了，reward+20
    elif graph[row][col] == '●':
        reward = 20

    # 控制边界约束, 防止越界异常
    row = max(0, row)
    row = min(r - 1, row)
    col = max(0, col)
    col = min(c - 1, col)
    # 返回下一个状态以及奖励
    return row, col, reward


# 在Python 3中，几乎所有的类都默认继承自object类，即使你不显式地写出来
class Solver(object):
    def __init__(self, r: int, c: int):
        """
        :param r: 代表当前地图行数
        :param c: 代表当前地图列数
        """
        # 初始化动作空间
        # 在Python中，大括号 {} 通常用来表示一个字典（dictionary）。
        # 字典是Python中一种内置的数据结构，用于存储键值对（key-value pairs）。
        # 每个键（key）都是唯一的，并且与一个值（value）相关联。
        self.idx_to_action = {0: '↑', 1: '↓', 2: '←', 3: '→', 4: 'O'}
        # 初始化地图行数、列数、动作个数
        self.r, self.c, self.action_nums = r, c, len(self.idx_to_action)
        # 随机初始化状态价值矩阵
        self.state_value_matrix = np.random.randn(r, c)
        # 随机初始化动作价值矩阵,这是一个三维矩阵
        # 这个矩阵用于表示在某个状态（由r和c指定）下，执行不同动作（由len(self.idx_to_action)确定）的“价值”或“评分”。
        self.action_value_matrix = np.random.randn(r, c, len(self.idx_to_action))
        # 随机初始化当前最优策略
        # self.cur_best_policy 被赋予了这个二维数组，它用于表示在当前学习或评估过程中，
        # 对于每个状态（由 r 行和 c 列定义的状态空间中的每个点），算法认为的最佳动作（或动作索引）。
        # 然而，由于这些值是随机抽取的，所以它们并不代表真正的最优策略，而只是作为初始值或某种随机策略的一部分。
        # np.random.choice 是 NumPy 库中的一个函数，用于从给定的一维数组中随机抽取元素，或者从指定的范围中随机生成整数
        # size=(r, c) 指定了输出数组的形状。
        # 因此，np.random.choice 会生成一个形状为 (r, c) 的二维数组，其中每个元素都是从上述范围内随机抽取的一个整数
        self.cur_best_policy = np.random.choice(len(self.idx_to_action), size=(r, c))
        self.cnt = 0

    # 打印当前的最优策略
    def show_policy(self):
        # [self.idx_to_action[idx] for idx in i] 是一个列表推导式，
        # 它遍历 i 中的每个元素（假设 i 是一个可迭代对象，比如列表或元组，且其元素是索引），
        # 并使用这些索引从 self.idx_to_action（假设这是一个字典或列表，将索引映射到动作名称或动作本身）中检索对应的动作。
        # 然后，print 函数的星号操作符 * 用于解包这个列表，使得列表中的每个元素都作为 print 函数的一个单独的位置参数，
        # 从而它们会被打印出来，并且默认会在它们之间添加空格作为分隔符。
        # 更具体的解释可以看本文代码后面的相关语法解析
        for i in self.cur_best_policy.tolist():
            print(*[self.idx_to_action[idx] for idx in i], sep=' ')

    # 显示地图
    def show_graph(self, graph):
        for i in graph:
            print(*i, sep=' ')

    # 清空控制台
    def clear_console(self):
        """
        通过os.name属性，可以获取一个字符串，该字符串表示Python正在运行的操作系统。
        对于Windows系统，os.name的值是'nt'（代表“New Technology”，是Windows NT及其后续版本的缩写）。
        对于大多数Unix-like系统（包括Linux和macOS），os.name的值是'posix'。
        对于代码 _ = os.system(...)：
            其使用了_（通常用作Python中的“don't care”变量，即一个用于接收不需要使用的值的变量名）来接收os.system(...)的返回值。
        如果不关心返回值的话，不写 _ 也是可以的，但这是一种良好的编程习惯
        """
        if os.name == 'nt':  # 对于 windows 系统
            _ = os.system('cls')
        else:  # 对于 Linux 和 mac
            _ = os.system('clear')

    # 打印点到点的动态运行过程
    def show_point_to_point(self, start_point, end_point, graph):
        # 越界检测
        assert (0 <= start_point[0] < self.r) and (
                0 <= start_point[1] < self.c), f'The start_point is {start_point}, is out of range.'
        assert (0 <= end_point[0] < self.r) and (
                0 <= end_point[1] < self.c), f'The end_point is {end_point}, is out of range.'

        # 记录起始点
        row, col = start_point
        i = 0
        # 开始展示动态运行过程
        while True:
            # 在起始点根据当前的最优策略选择采取的行动
            graph[row][col] = self.idx_to_action[self.cur_best_policy[row][col]]
            # 选择行动之后，清空控制台
            self.clear_console()
            # 显示地图
            self.show_graph(graph)
            # 为了方便观察，沉睡 0.5 s
            time.sleep(0.5)
            # 根据最优策略选择action后所进入的下一个状态[row][col]以及对应得到的 reward 值
            # 对于打印动态运行过程来说 reward 并没有用，因此这里没有接收 reward 值
            row, col, _ = get_reward((row, col), self.cur_best_policy[row][col], graph)
            # 循环退出条件为：要么已经到达最终状态，要么i已经大于了 r*c 大小
            # 因为如果进行轮次数 i 已经比网格世界的格子数还大了，那么说明无解，当然可以结束
            if (row, col) == end_point or i > self.r * self.c:
                break
            # 轮次数量+1
            i += 1

        # epsilon 贪婪法，当 epsilon = 0，完全贪婪法

    def get_epsilon_greedy_action(self, state, epsilon=0.1):
        row, col = state
        # 找最优动作
        best_action = np.argmax(self.action_value_matrix[row][col]).item()
        # epsilon贪婪法，当 epsilon != 0时，才有可能进入该 if 语句，否则直接返回最优动作
        """
        < 右侧的式子表示的是 greedy action 被选择的概率
        < 左侧的式子表示的是其它的 action 被选择的概率
        使用 random.random 随机数与 greedy action 的概率值进行随机比较这样才不会总是返回最优动作
        同时这样的做法也会更倾向于选择概率值较大的 greedy action
        """
        if random.random() < epsilon * (self.action_nums - 1) / self.action_nums:
            # 随机选择除了当前最佳 action 之外的其它 action
            # 因为其它的 action 被选择的概率都是一样的，所以随机选就可以
            actions = list(self.idx_to_action.keys())
            actions.remove(best_action)
            return random.choice(actions)
        return best_action

    def mplot(self, x, y, ax, fmt, title, x_label, y_label, legend):
        ax.plot(x, y, fmt)
        ax.set_xlim(x[0], x[-1] + 0.4)  # 设置X轴范围
        # ax.set_xticks(x)  # 用于设置X轴上要显示的刻度值
        ax.set_xlabel(x_label)
        ax.set_ylabel(y_label)
        ax.legend(legend)
        ax.set_title(title)


class Sarsa(Solver):
    def __init__(self, r: int, c: int):
        super(Sarsa, self).__init__(r, c)

    # Sarsa 的算法公式模拟
    def _update(self, cur_state, cur_action, reward, next_state, next_action, alpha_k=1e-1, gama=0.9):
        cur_row, cur_col = cur_state
        next_row, next_col = next_state
        # 先取出当前状态所选取动作的动作价值
        cur_action_value = self.action_value_matrix[cur_row, cur_col, cur_action]
        # 然后取出下一状态所选取动作的动作价值
        next_action_value = self.action_value_matrix[next_row, next_col, next_action]
        # 通过公式更新下一时刻的动作价值
        next_action_value = cur_action_value - alpha_k * (cur_action_value - reward - gama * next_action_value)
        # 将更新后的值写回动作价值矩阵
        self.action_value_matrix[cur_row, cur_col, cur_action] = next_action_value

    def update(self, epoch, graph, start_state=None, alpha_k=1e-1, gama=0.9):
        # 指定起点
        cur_state = start_state
        cache = []
        for i in range(epoch):
            # 起点随机生成
            if start_state is None:
                cur_state = (random.randint(0, self.r - 1), random.randint(0, self.c - 1))  # 随机生成初始状态
            else:
                cur_state = start_state
            cur_action = self.get_epsilon_greedy_action(cur_state)
            j = 0  # 记录每一轮 epoch 所走的 episode 长度
            # 如果没有到达最终点
            while graph[cur_state[0]][cur_state[1]] != '●':
                *next_state, reward = get_reward(cur_state, cur_action, graph)
                next_action = self.get_epsilon_greedy_action(next_state)
                self._update(cur_state, cur_action, reward, next_state, next_action, alpha_k, gama)
                cur_state = next_state
                cur_action = next_action
                j += 1
            cache.append(j)

        _, axs = plt.subplots(1, 1, figsize=(4, 3), dpi=150)
        self.mplot(list(range(len(cache))), cache, axs, 'b', 'Episode long changed', 'Episode index', 'Episode length',
                   ['Sarsa'])
        # plt.savefig("./2.png", bbox_inches='tight')  # 这里有横轴截断问题
        plt.tight_layout()
        plt.show()

        # 最后收敛的状态价值矩阵
        self.state_value_matrix = np.max(self.action_value_matrix, axis=2)  # 状态价值矩阵
        # 最优策略
        self.cur_best_policy = np.argmax(self.action_value_matrix, axis=2)  # 当前最优策略
        self.cur_best_policy[cur_state[0], cur_state[1]] = 4  # '●'动作为原地转圈，在训练过程中我们没有赋值


if __name__ == "__main__":
    # 定义地图,□ 表示可以正常走的，× 表示 forbidden area，● 表示终点
    graph = [['□', '□', '□', '□', '□'],
             ['□', '×', '×', '□', '□'],
             ['□', '□', '×', '□', '□'],
             ['□', '×', '●', '×', '□'],
             ['□', '×', '□', '□', '□']]
    r = len(graph)
    c = len(graph[0])

    start_state = (0, 0)
    end_point = (3, 2)  # 改地图的时候注意改终点坐标位置

    """Sarsa"""
    sarsa_iterator = Sarsa(r, c)
    sarsa_iterator.update(500, graph, start_state=start_state)  # 指定起点
    # sarsa_iterator.update(2000, graph)  # 随机起点
    sarsa_iterator.show_policy()
    sarsa_iterator.show_point_to_point(start_state, end_point, graph)

关于这个算法最后再强调一些内容：

例子例证 Sarsa：

TD learning of action values： Expected Sarsa

这一小节的 Expected Sarsa 和 下一小节的 N-step Sarsa 是上面 Sarsa 算法的一些变形，它们的重要性是没有 Sarsa 高的，但是这里也一并简单介绍一下。

首先是 Expected Sarsa：

TD learning of action values： N-step Sarsa

然后是 N-step Sarsa：

TD learning of action values： Q-Learning

接下来就来到了 Q-learning，万众瞩目的时刻，Q-learning 是非常非常经典的一种算法，直到今天Q-learning也在被广泛地使用，当然指的是 Deep Q-learning，也就是 Q-learning 的一种变形。

Q-learning 和 Sarsa 以及之前介绍的算法主要有什么区别呢？

从数学上说，Q-learning 是直接估计 optimal action value，所以它不需要去做 policy evaluation 和 policy improvement 这两个之间来回交替运行，因为它直接就把最优的 action value 给估计出来了。

直接给出 Q-learning 的算法，再来慢慢分析它的性质：

可以看到 Q-learning 和 之前的 Sarsa 算法是非常类似的，从结构上讲基本一模一样，唯一不同的地方在于等式右边的 TD target 发生了变化，这在上图中也可以看到。

那么 Q-learning 在数学上解决什么问题呢？

之前说 Sarsa 是在求解一个贝尔曼方程，而 Q-learning 就不一样了，它是在求解一个贝尔曼最优方程也就是下图中的这样一个式子：

Q-learning 求解的是贝尔曼最优方程，但是这个贝尔曼最优方程和之前所介绍的贝尔曼最优方程不一样，这里面第一个是它有一个 expectation，第二个是它不是基于 state value 而是基于 action value的。尽管如此，但它依然是一个贝尔曼最优方程，证明可以参考赵老师的书籍。

我们只要知道 Q-learning 实际上就是求解这样一个贝尔曼最优公式就行了，其最后求解得到的 q 值并非是说哪一个策略的 q 值而是最优的 q 值。当然这个最优的 q 值是对应的最优的那个策略。

下面再介绍一些 Q-learning 的性质：

第一个是关于 on-policy 和 off-policy。

但这个不是针对 Q-learning 的，实际上它是对所有的强化学习的算法都存在这样一个问题，这里借着介绍 Q-learning 这次就引入 on-policy 和 off-policy 的概念：

在强化学习中存在两种策略，第一个是 behavior policy，这个策略和环境交互然后生成 experience。第二个策略是 target policy，这个策略就是我们一直去更新它然后最后这个 target policy 就是我们想要的最优的策略。

基于这两个内容由此我们就可以定义出 on-policy 和 off-policy 两种强化学习的算法。

on-policy 的意思就是你的 behavior 策略和 target 策略是相同的。也就是使用策略来和环境进行交互然后得到 experience 同时我再改进这个策略，改进完了之后我们再用这个策略和环境进行交互（实时优化）。

off-policy 的意思就是 behavior 策略和 target 策略是不相同的。比如说使用一个策略来和环境交互得到大量的经验然后使用这些经验不断地去改进一个策略然后那个策略最后会收敛到一个最优的策略（事后优化）。

引入 on-policy 和 off-policy 的目的是什么呢？因为稍后会介绍前面所学的 Sarsa 实际上是一种 on-policy 的算法，而 Q-learning 既可以是一种 off-policy，也可以是一种 on-policy 的算法。

下面是 off-policy 的好处：

off-policy 最直接的好处就是我们可以从之前别人的那些经验当中，也就是它们采取了它们自己的策略然后积累了一些经验对于这些经验我们可以直接拿过来然后去学习。

如何判断一个 TD 算法是 on-policy 的还是 off-policy 的：

判断时有两个工具，一个是要知道这个算法在数学上究竟是在解决一个什么样的数学问题；还有一个就是可以看一下这个算法它在实施的过程当中需要哪些东西才能让这个算法给跑起来。根据这些需要的东西其实就可以来判断它究竟是 on-policy 还是 off-policy 。

下面就来看这三个算法如何使用上面说的这两个工具来判断其是 on-policy 还是 off-policy 的：

Q-learning 的伪代码实现，共有两种版本。

Q-learning 的 on-policy 版本实际上和 Sarsa 是一模一样的，唯一的区别就是在 q value 这一部分：

整个流程就是开始有一个策略，然后根据整个策略我得到了一些数据，我通过这些数据我得到了 q value ，我通过这个 q value 我得到了一个改进的策略，我再通过这个改进的策略再进一步得到数据，那显然这里边这个策略它实际上既是用来生成数据的也就是它是 behavior policy 同时它又在不断的更新，所以它是 target policy，因此这个时候它就是 on-policy 。

下面是 off-policy 的版本：

Q-learning Implementation

class Qlearning(Solver):
    def __init__(self, r, c):
        super(Qlearning, self).__init__(r, c)

    def _update(self, cur_state, cur_action, reward, next_state, next_action, alpha_k=1e-1, gama=0.9):
        cur_row, cur_col = cur_state
        next_row, next_col = next_state
        cur_action_value = self.action_value_matrix[cur_row, cur_col, cur_action]
        next_action_value = np.max(self.action_value_matrix[next_row, next_col])  # 这里改进了。。。。与Sarsa不同，其余都一样
        next_action_value = cur_action_value - alpha_k * (cur_action_value - reward - gama * next_action_value)
        self.action_value_matrix[cur_row, cur_col, cur_action] = next_action_value

    def update(self, epoch, graph, start_state=None, epsilon=0.1, alpha_k=1e-1, gama=0.9):
        # 指定起点
        cur_state = start_state
        cache = []
        for i in range(epoch):
            # 起点随机生成
            if start_state is None:
                cur_state = (random.randint(0, self.r - 1), random.randint(0, self.c - 1))  # 随机生成初始状态
            else:
                cur_state = start_state
            cur_action = self.get_epsilon_greedy_action(cur_state, epsilon=epsilon)
            j = 0
            while graph[cur_state[0]][cur_state[1]] != '●':
                *next_state, reward = get_reward(cur_state, cur_action, graph)
                # epsilon为1的时候就是离线学习，否则就是在线学习
                next_action = self.get_epsilon_greedy_action(next_state, epsilon=epsilon)
                self._update(cur_state, cur_action, reward, next_state, next_action, alpha_k, gama)
                cur_state = next_state
                cur_action = next_action
                j += 1
            cache.append(j)

        _, axs = plt.subplots(1, 1, figsize=(4, 3), dpi=150)
        self.mplot(list(range(len(cache))), cache, axs, 'b', 'Episode long changed', 'Episode index', 'Episode length',
                   ['Qlearning'])
        # plt.savefig("./2.png", bbox_inches='tight')  # 这里有横轴截断问题
        plt.tight_layout()
        plt.show()

        # 最后收敛的状态价值矩阵
        self.state_value_matrix = np.max(self.action_value_matrix, axis=2)  # 状态价值矩阵
        # 最优策略
        self.cur_best_policy = np.argmax(self.action_value_matrix, axis=2)  # 当前最优策略
        self.cur_best_policy[cur_state[0], cur_state[1]] = 4  # '●'动作为原地转圈，在训练过程我们没有赋值

直接将这段代码复制进上面 Sarsa 部分代码中运行即可，这里是为了避免多余的复制因此只放了算法代码。

举几个例子：

A unified point of view

Q-learning 是 off-policy 的，我们也通过例子看了怎么使用 off-policy 的 Q-learning 来学习最优的策略。

实际上 off-policy 的性质是非常重要的，之后我们会学习 Deep Q-learning，为什么将神经网络和 TD 算法相结合的时候会选择 Q-learning 呢，这里面的 off-policy 的性质其实发挥了非常重要的作用。

这一节就是简单对所有的 TD 算法做个小总结：

这些 TD 方法从本质上说是来求解一个给定策略的贝尔曼公式，但是我怎么让它来搜索最优的策略呢？其实就是我把这个 policy evaluation 这个步骤和 policy improvement 相结合我就可以来得到一个搜索最优策略的这样一个算法。

而对于蒙特卡洛算法其实也是来求解这么一个式子，这个式子其实你可以说它是贝尔曼公式，实际上它是 action value 的一个最基本的定义。

Summary

没啥好总结的了，基本就是各个章节的内容，因为介绍的都是各种算法嘛。