模拟退火算法SA求解多维连续函数极值

最新推荐文章于 2024-04-23 09:25:38 发布

霸道小明

最新推荐文章于 2024-04-23 09:25:38 发布

阅读量1.4k

点赞数 1

分类专栏：优化算法文章标签：算法 matlab 模拟退火算法机器学习

本文链接：https://blog.csdn.net/qq_54169998/article/details/126690534

版权

优化算法专栏收录该内容

12 篇文章 0 订阅

订阅专栏

一、模拟退火算法原理

模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却。加温时，固体内部粒子随温升变为无序状，内能增大;而徐徐冷却时粒子渐趋有序，在每个温度上都达到平衡态，最后在常温时达到基态，内能减为最小。根据Metropolis准则，粒子在温度 $T$ 时趋于平衡的概率为 $exp(-\Delta E/T)$ ，其中 $E$ 为温度T时的内能， $\Delta E$ 为其改变量。用固体退火模拟组合优化问题，将内能E模拟为目标函数值，温度 $T$ 演控制参数，即得到解组合优化问题的模拟退火算法:由初始解 $X_{0}$ 和控制参数初值 $T$ 开始，对当前解重复“产生新解→计算目标函数差接受或舍弃”的迭代，并逐步减小 $T$ 值，算法终止时的当前解即为所得近似最优解，这是基于MonteCarlo迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表控制，包括控制参数的初值 $T$ 。及其衰减因子 $K$ 、每个工值时的迭代次数工和停止条件。

二、模拟退火算法思想

模拟退火的主要思想是:在搜索区间随机游走(即随机选择点),再利用Metropolis抽样准则，使随机游走逐渐收敛于局部最优解。而温度是Metropolis算法中的一个重要控制参数，可以认为这个参数的大小控制了随机过程向局部或全局最优解移动的快慢。

Metropolis是一种有效的重点抽样法，其算法为:系统从一个能量状态变化到另一个状态时，相应的能量从 $E_{1}$ 变化到 $E_{2}$ ,其概率为

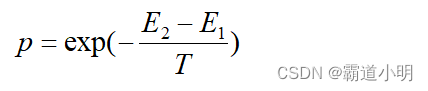
如果 $E_{1}<E_{2}$ ，系统接受此状态:否则，以一个随机的概率接受或丢弃此状态。状态2被接受的概率为

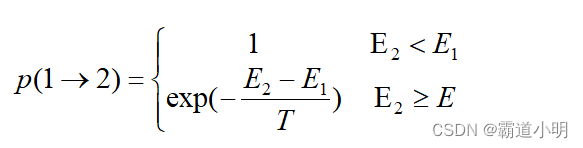
这样经过一一定次数的选代，系统会逐渐趋于一个稳定的分布状态。

三、模拟退火算法流程

模拟退火算法新解的产生和接受可分为如下三个步骤:

(1)由一个产生函数从当前解产生-一个位于解空间的新解:为便于后续的计算和接受，减少算法耗时，通常选择由当前解经过简单变换即可产生新解的方法。注意，产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。

(2)判断新解是否被接受，判断的依据是一个接受准则，最常用的接受准则是Metropolis准则:若 $\Delta E<0$ ，则接受 $X{}'$ 作为新的当前解 $X$ ;否则，以概率 $exp(-\Delta AE /T)$ 接受 $X{}'$ 作为新的当前解 $X$ 。

(3)当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。此时，当前解实现了一次迭代，可在此基础上开始下一轮试验。若当新解被判定为舍弃，则在原当前解的基础上继续下一轮试验。

模拟退火算法求得的解与初始解状态(算法迭代的起点)无关，具有渐近收敛性，已在理论上被证明是一种以概率 1收敛于全局最优解的优化算法。模拟退火算法可以分解为解空间、目标函数和初始解三部分。该算法具体流程如下:

(1)初始化:设置初始温度 $T_{0}$ (充分大)、初始解状态 $X_{0}$ (是算法迭代的起点)、每个 $T$ 值的迭代次数 $L$

(2)对 $k=1,...,L$ 做第(3)至第(6)步:

(3)产生新解 $X$ ;

(4)计算增量 $\Delta E=E(X{}')-E(X)$ ，其中 $E(X)$ 为评价函数:

(5)若 $\Delta E<0$ ，则接受 $X{}'$ 作为新的当前解，否则以概率 $exp(-\Delta E/T)$ 接受 $X{}'$ 作为新的当前解;

(6)如果满足终止条件，则输出当前解作为最优解，结束程序;

(7) $T$ 逐渐减小，且 $T\rightarrow 0$ ，然后转第(2)步。

模拟退火算法流程如图所示。

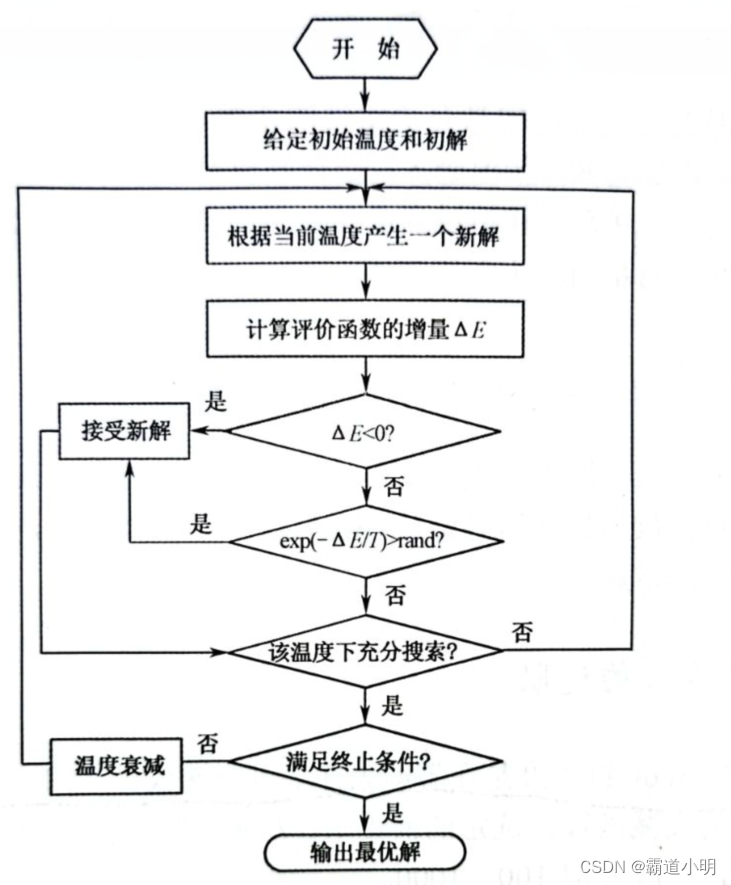
四、关键参数说明

状态产生函数

设计状态产生函数应该考虑到尽可能地保证所产生的候选解遍布全部解空间。一般情况下状态产生函数由两部分组成，即产生候选解的方式和产生候选解的概率分布。候选解的产生方式由问题的性质决定，通常在当前状态的邻域结构内以一.定概率产生。

初温

温度T在算法中具有决定性的作用，它直接控制着退火的走向。由随机移动的接受准则可知:初温越大，获得高质量解的几率就越大，且Metropolis的接收率约为1。然而，初温过高会使计算时间增加。为此，可以均匀抽样一组状态，以各状态目标值的方差为初温。

退温函数

退温函数即温度更新函数，用于在外循环中修改温度值。目前，最常用的温度更新函数为指数退温函数，即 $T(n+ 1)=K\times T(n)$ ，其中 $0<K<l$ 是一个非常接近于1的常数。

Markov链长度L的选取

Markov链长度是在等温条件下进行迭代优化的次数，其选取原则是在衰减参数T的衰减函数已选定的前提下，L应选得在控制参数的每一取值上都能恢复准平衡，一般L取100~ 1000.

算法停止准则

算法停止准则用于决定算法何时结束。可以简单地设置温度终值 $T_{f}$ 当 $T=T_{f}$ 时算法终止。然而，模拟火算法的收敛性理论中要求T，趋向于零，这其实是不实际的。常用的停止准则包:设置终止温度的國值，设置迭代次数阈值，或者当搜索到的最优值连续保持不变时停止搜索。

五、例题

计算函数 $f(x)=\sum_{n}^{i=1}x_{i}^{2}(-20\leqslant x\leqslant 20)$ 的最小值，其中个体 $x$ 的维数n=10。这是一个简单平方和函数，只有一个极小点，理论最小值 $f(0,0,...,0)=0$ 。

解:仿真过程如下:
(1)初始化Markov链长度为L = 200，衰减参数为K = 0.998，步长因子为S= 0.01,初始温度为T= 100，容差为YZ= 1X10~8；随机产生初始解，并计算其目标函数值。
(2)在变量的取值范围内，按步长因子随机产生新解，并计算新目标函数值；以Metropolis算法确定是否替代旧解，在一种温度下，迭代L次。
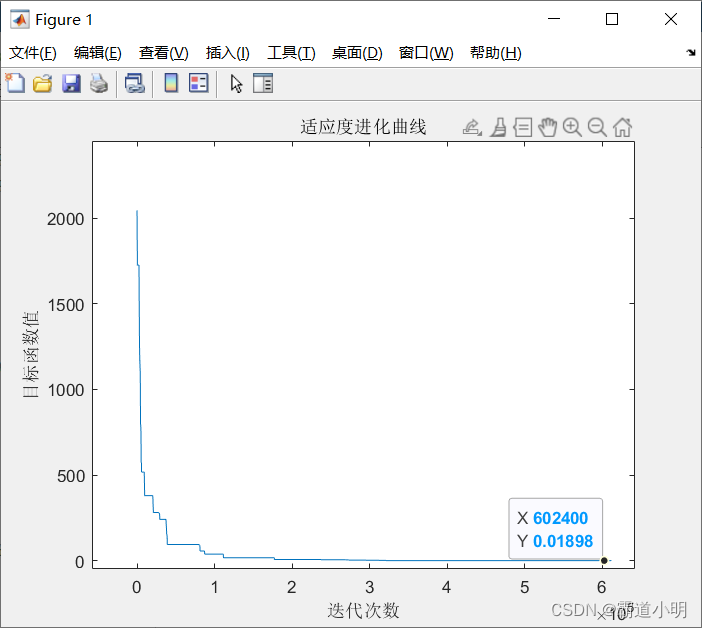
(3)判断是否满足终止条件:若满足，则结束搜索过程，输出优化值;若不满足，则减小温度，进行迭代优化。优化结束后，其适应度进化曲线如图所示。优化后的结果为:x= [-0.0282
0.0046 . -0.0158 0.0265 0.0345 0.0436 -0.0467 0.0006 0.0179 -0.0282]，函数f(x)的
最小值为8.156x10-3。

%%%%%%%%%%%%%%%%%%%%%%模拟退火算法解决函数极值%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;                      %清除所有变量
close all;                      %清图
clc;                            %清屏
D=10;                           %变量维数 
Xs=20;                          %上限                                
Xx=-20;                         %下限
%%%%%%%%%%%%%%%%%%%%%%%%%%%冷却表参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
L = 200;                        %马可夫链长度
K = 0.998;                      %衰减参数
S = 0.01;                       %步长因子
T=100;                          %初始温度
YZ = 1e-8;                      %容差
P = 0;                          %Metropolis过程中总接受点
%%%%%%%%%%%%%%%%%%%%%%%%%%随机选点 初值设定%%%%%%%%%%%%%%%%%%%%%%%%%
PreX = rand(D,1)*(Xs-Xx)+Xx;
PreBestX = PreX;
PreX =  rand(D,1)*(Xs-Xx)+Xx;
BestX = PreX;
%%%%%%%%%%%每迭代一次退火一次(降温), 直到满足迭代条件为止%%%%%%%%%%%%
deta=abs( func1( BestX)-func1(PreBestX));
while (deta > YZ) && (T>0.001)
    T=K*T; 
    %%%%%%%%%%%%%%%%%%%%%在当前温度T下迭代次数%%%%%%%%%%%%%%%%%%%%%%
    for i=1:L  
        %%%%%%%%%%%%%%%%%在此点附近随机选下一点%%%%%%%%%%%%%%%%%%%%%
            NextX = PreX + S* (rand(D,1) *(Xs-Xx)+Xx);
            %%%%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%%%%%%%%%%%%
            for ii=1:D
                if NextX(ii)>Xs | NextX(ii)<Xx
                    NextX(ii)=PreX(ii) + S* (rand *(Xs-Xx)+Xx);
                end
            end            
        %%%%%%%%%%%%%%%%%%%%%%%是否全局最优解%%%%%%%%%%%%%%%%%%%%%%
        if (func1(BestX) > func1(NextX))
            %%%%%%%%%%%%%%%%%%保留上一个最优解%%%%%%%%%%%%%%%%%%%%%
            PreBestX = BestX;
            %%%%%%%%%%%%%%%%%%%此为新的最优解%%%%%%%%%%%%%%%%%%%%%%
            BestX=NextX;
        end
        %%%%%%%%%%%%%%%%%%%%%%%% Metropolis过程%%%%%%%%%%%%%%%%%%%
        if( func1(PreX) - func1(NextX) > 0 )
            %%%%%%%%%%%%%%%%%%%%%%%接受新解%%%%%%%%%%%%%%%%%%%%%%%%
            PreX=NextX;
            P=P+1;
        else
            changer = -1*(func1(NextX)-func1(PreX))/ T ;
            p1=exp(changer);
            %%%%%%%%%%%%%%%%%%%%%%%%接受较差的解%%%%%%%%%%%%%%%%%%%%
            if p1 > rand        
                PreX=NextX;
                P=P+1;         
            end
        end
    trace(P+1)=func1( BestX);    
    end
    deta=abs( func1( BestX)-func1 (PreBestX)); 
end
disp('最小值在点:');
BestX
disp( '最小值为:');
func1(BestX)
figure
plot(trace(2:end))
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%%%%%%%
function result=func1(x)
summ=sum(x.^2);
result=summ;
end

霸道小明

关注

1
点赞
踩
13

收藏

觉得还不错? 一键收藏
2
评论
模拟退火算法SA求解多维连续函数极值

(1)由一个产生函数从当前解产生-一个位于解空间的新解:为便于后续的计算和接受，减少算法耗时，通常选择由当前解经过简单变换即可产生新解的方法。模拟退火算法求得的解与初始解状态(算法迭代的起点)无关，具有渐近收敛性，已在理论上被证明是一种以概率 1收敛于全局最优解的优化算法。Markov链长度是在等温条件下进行迭代优化的次数，其选取原则是在衰减参数T的衰减函数已选定的前提下，L应选得在控制参数的每一取值上都能恢复准平衡，一般L取100~ 1000.，系统接受此状态:否则，以一个随机的概率接受或丢弃此状态。
复制链接

扫一扫