R语言的线性优化(一元、多元、约束条件)

最新推荐文章于 2023-08-27 05:51:41 发布

hence..

最新推荐文章于 2023-08-27 05:51:41 发布

阅读量3k

点赞数 5

分类专栏： R语言数据分析文章标签： r语言开发语言

本文链接：https://blog.csdn.net/qq_54423921/article/details/125214669

版权

R语言数据分析专栏收录该内容

34 篇文章

订阅专栏

R语言的线性优化(一元、多元、约束条件）

一元函数优化求解
多元函数优化求解
带约束条件的函数优化

一元函数优化求解

R做一元函数优化求解得函数是optimize或者optimise
在这里插入图片描述
$\text{以函数} \ln x-x^2\text{为例}$ ，现在分别在[1,4]上这个函数的最大值，最小值

f<-function(x) log(x)-x^2;f#定义函数f
curve(f,xlim=c(1,4))#画出f在1,4上的函数图像
optimise(f,interval = c(1,4),tol=0.0001)#默认求最小值
optimise(f,interval = c(1,4),tol=0.0001,maximum = T)#添加参数求最大值

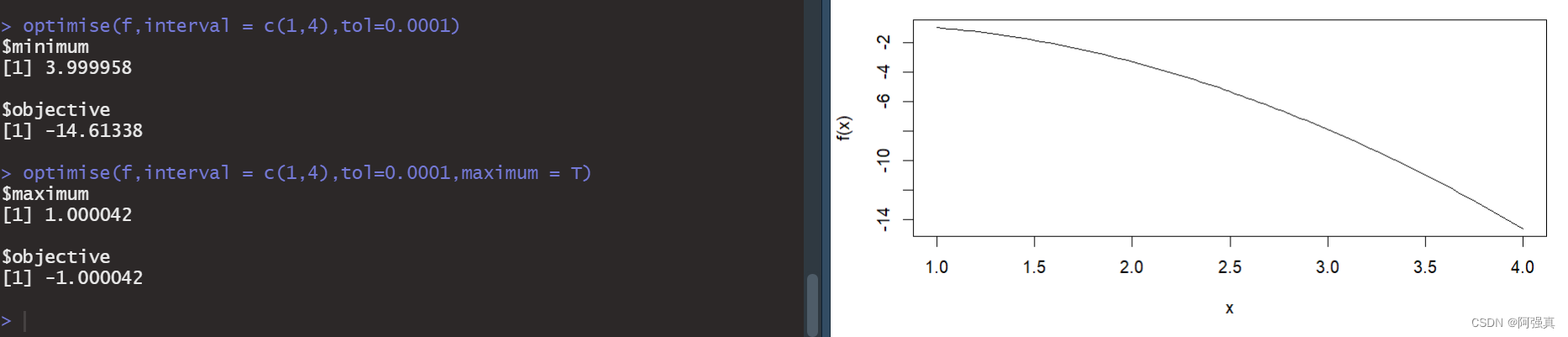
在这里插入图片描述
可以看出这个函数在我定义区间上的最大值和最小值，和此时x的取值
如果你想用ggplot绘制函数，可以这样：

a <- seq(1,4,0.001);b <- log(a)-a^2;c <- data.frame(a,b);c
ggplot(c,aes(a,b))+geom_point(size=0.5)+
  labs(x=quote(x),y=quote(lnx-x^2))+
  theme_economist()

在这里插入图片描述

多元函数优化求解

多元函数优化求解得命令是optim，其基本用法是:
在这里插入图片描述
$\text{求解函数}f\left( x,y \right) =\left( x^2+y-11 \right) ^2+\left( x+y^2-7 \right) ^2\text{的极值}$

x1 <- x2 <- seq(-10,10,length=100)
fr2 <- function(x){
  x1=x[1]
  x2=x[2]
  (x1^2+x2-11)^2+(x1+x2^2-7)^2
}
persp(x1,x2,z,box=T,border=T,theta=45,phi=35,col="purple")#画三维图
optim(c(-5,5),fr2)

在这里插入图片描述

带约束条件的函数优化

$\text{求解函数}f\left( x,y \right) =\left( {x_1}^2+x_2-11 \right) ^2-\left( x_1+{x_2}^2-7 \right) ^2\text{，}x_1>0,x_2>0\text{的极值}$
这里要用到constrOptim函数：
在这里插入图片描述

x1 <- x2 <- seq(-10,10,length=100)
fr2 <- function(x){
  x1=x[1]
  x2=x[2]
  (x1^2+x2-11)^2+(x1+x2^2-7)^2
}
ui<-matrix(c(1,0,0,1),nc=2);ui
ci <- c(0,0)
constrOptim(c(0.2,0.5),grad=NULL,fr2,ui=ui,ci=ci)

在这里插入图片描述