💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
三、全局准则法(Global Criterion Method)
💥1 概述
多目标优化方法及Lq范数理想点研究
一、加权法(Weighted Sum Method)
-
基本原理
加权法通过赋予各目标函数权重wkwk,将其线性组合为单一目标函数:

权重wk反映目标的重要性,归一化后简化优化问题为单目标求解。 -
权重参数为0/1时的退化分析
- 当某一权重wi=1,其余wj=1时,优化问题退化为单目标优化,仅优化fi(X)。例如,中取w1=w2=0.5平衡体积与传动效率,若w1=1则仅优化体积。
- 局限性:权重选择依赖先验知识,且可能因目标函数量级差异导致解偏向某一目标。
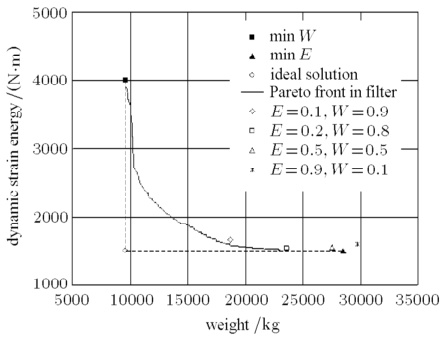
二、ε-约束法(ε-Constrained Method)
- 基本原理
将某一目标作为主优化目标,其余目标转化为约束:

通过调整εi探索Pareto前沿。
-
ε参数为0/1时的退化分析
- 当εi=0时,约束条件变为fi(X)≤0,若目标函数非负,则等价于仅优化主目标。
- 例如,在电力系统优化中,将响应时间约束为ε=0,则仅优化成本。
-
优缺点
- 优点:直接生成Pareto解,适用于非凸目标空间。
- 缺点:高维问题计算复杂度高,且εiεi设置需反复尝试。
三、全局准则法(Global Criterion Method)
-
基本原理
通过构造全局准则(如最小化与理想点的距离)综合优化多个目标:
-
参数设置的兼容性
- 当准则权重偏向某一目标时(如g1=1,g2=0g1=1,g2=0),退化为单目标优化。
- 例如,冰蓄冷系统中调节g1g1和g2g2可分别偏向成本或能耗。
-
优缺点
- 优点:避免加权法的量级敏感问题,直接逼近理想点。
- 缺点:需预先计算理想点,且准则函数可能非凸。
四、Lq范数理想点研究
-
数学定义

常见q=1,2,∞分别对应曼哈顿、欧式、切比雪夫距离。 -
计算方法与实现
- 步骤1:分别求解各单目标优化问题,获取理想点f∗f∗。
- 步骤2:通过网格搜索或优化算法最小化Lq(X)Lq(X)。
- Matlab示例:通过
fmincon求解不同qq值的全局准则。
-
应用案例
- 在AUV优化中,计算Lq范数选择Pareto解,如最小化阻力与体积的综合距离。
- 精密空调控制中,以理想点指导温湿度协同优化。
五、文献综述:理想点研究进展
-
理论发展
- 理想点定义:最早由Pareto提出,后经Kuhn-Tucker条件完善。
- 扩展概念:纳迪尔点(Nadir Point)作为目标最劣解的参考,用于评估解集扩展性。
-
应用领域
- 工程优化:如涡轮叶片设计、冰蓄冷系统。
- 决策分析:TOPSIS方法结合理想点与负理想点进行方案排序。
-
挑战与趋势
- 动态理想点:在不确定环境中实时更新理想点。
- 多目标集成:结合加权法、ε-约束法提升解集多样性。
六、结论
-
方法对比
方法 退化条件 优点 缺点 加权法 权重为0/1 简单易实现 权重敏感,量级影响大 ε-约束法 ε=0或严格约束 直接生成Pareto解 高维计算复杂 全局准则法 权重偏向单一目标 避免量级问题 需预计算理想点 -
未来方向
- 自适应参数调整:如动态权重或ε值。
- 混合算法设计:结合Pareto前沿搜索与Lq范数评估。
📚2 运行结果




运行结果图比较多,后面的运行结果去掉Matlab图框。























部分代码:
%% Instructions:
% Verify that all of the following files exist before hitting 'Run':
% 'GRID_results.mat'
% 'ALL_results.mat'
% 'fmincon_results.mat'
% 'penalty_results.mat'
% 'penalty2_results.mat'
% ('ALM_results.mat')
% 'fminimax_results.mat'
% 'Lq1_results.mat'
% 'Lq2_results.mat'
% 'LqInf_results.mat'
% 'EC_results.mat'
% 'EC2_results.mat'
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% clean up
close all
clear
clc
[d_L, d_U, t_L, t_U, L_L, L_U, ~, ~] = set_Lims();
%% GRID
GRID_res = load('GRID_results.mat');
f1_s_GRID = GRID_res.f1_s;
f2_s_GRID = GRID_res.f2_s;
%% all "optima"
ALL_res = load('ALL_results.mat');
X = ALL_res.X;
f1 = ALL_res.f1;
f2 = ALL_res.f2;
f1_s = ALL_res.f1_s;
f2_s = ALL_res.f2_s;
Lq1 = ALL_res.Lq1;
Lq2 = ALL_res.Lq2;
LqInf = ALL_res.LqInf;
% select the Lq1 norm from the full set of all optima
[~, idx] = min(Lq1);
X_LQ1 = X(idx, :);
f1_LQ1 = f1(idx);
f2_LQ1 = f2(idx);
f1_s_LQ1 = f1_s(idx);
f2_s_LQ1 = f2_s(idx);
% select the Lq2 norm from the full set of all optima
[~, idx] = min(Lq2);
X_LQ2 = X(idx, :);
f1_LQ2 = f1(idx);
f2_LQ2 = f2(idx);
f1_s_LQ2 = f1_s(idx);
f2_s_LQ2 = f2_s(idx);
% select the LqInf norm from the full set of all optima
[~, idx] = min(LqInf);
X_LQinf = X(idx, :);
f1_LQinf = f1(idx);
f2_LQinf = f2(idx);
f1_s_LQinf = f1_s(idx);
f2_s_LQinf = f2_s(idx);
% extract good and bad values from all optima
f1_g = min(f1);
f1_b = max(f1);
f2_b = min(f2);
f2_g = max(f2);
%% fmincon
fmincon_res = load('fmincon_results.mat');
X_fmincon = fmincon_res.X;
f1_fmincon = fmincon_res.f1;
f2_fmincon = fmincon_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_fmincon))
f1_s_fmincon(i,:) = (f1_fmincon(i) - f1_g)/(f1_b - f1_g);
f2_s_fmincon(i,:) = (f2_fmincon(i) - f2_g)/(f2_b - f2_g);
end
%% Penalty Method
penalty_res = load('penalty_results.mat');
X_penalty = penalty_res.X;
f1_penalty = penalty_res.f1;
f2_penalty = penalty_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_penalty))
f1_s_penalty(i,:) = (f1_penalty(i) - f1_g)/(f1_b - f1_g);
f2_s_penalty(i,:) = (f2_penalty(i) - f2_g)/(f2_b - f2_g);
end
% second chosen start point
penalty2_res = load('penalty2_results.mat');
X_penalty2 = penalty2_res.X;
f1_penalty2 = penalty2_res.f1;
f2_penalty2 = penalty2_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_penalty2))
f1_s_penalty2(i,:) = (f1_penalty2(i) - f1_g)/(f1_b - f1_g);
f2_s_penalty2(i,:) = (f2_penalty2(i) - f2_g)/(f2_b - f2_g);
end
% combine both sets of the penalty method results
X_penalty = [X_penalty; X_penalty2];
f1_penalty = [f1_penalty; f1_penalty2];
f2_penalty = [f2_penalty; f2_penalty2];
f1_s_penalty = [f1_s_penalty; f1_s_penalty2];
f2_s_penalty = [f2_s_penalty; f2_s_penalty2];
% %% Augmented Lagrangian Method (ALM)
% ALM_res = load('ALM_results.mat');
% X_ALM = ALM_res.X;
% f1_ALM = ALM_res.f1;
% f2_ALM = ALM_res.f2;
%
%
% for i = 1:max(size(f1_ALM))
% f1_s_ALM(i,:) = (f1_ALM(i) - f1_g)/(f1_b - f1_g);
% f2_s_ALM(i,:) = (f2_ALM(i) - f2_g)/(f2_b - f2_g);
% end
%% fminimax
fminimax_res = load('fminimax_results.mat');
X_fminimax = fminimax_res.X_opt;
f1_fminimax = fminimax_res.f1;
f2_fminimax = fminimax_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_fminimax))
f1_s_fminimax(i,:) = (f1_fminimax(i) - f1_g)/(f1_b - f1_g);
f2_s_fminimax(i,:) = (f2_fminimax(i) - f2_g)/(f2_b - f2_g);
end
%% Global Criterion (Lq)
Lq1_res = load('Lq1_results.mat');
X_Lq1 = Lq1_res.X_opt;
f1_Lq1 = Lq1_res.f1;
f2_Lq1 = Lq1_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_Lq1))
f1_s_Lq1(i,:) = (f1_Lq1(i) - f1_g)/(f1_b - f1_g);
f2_s_Lq1(i,:) = (f2_Lq1(i) - f2_g)/(f2_b - f2_g);
end
Lq2_res = load('Lq2_results.mat');
X_Lq2 = Lq2_res.X_opt;
f1_Lq2 = Lq2_res.f1;
f2_Lq2 = Lq2_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_Lq2))
f1_s_Lq2(i,:) = (f1_Lq2(i) - f1_g)/(f1_b - f1_g);
f2_s_Lq2(i,:) = (f2_Lq2(i) - f2_g)/(f2_b - f2_g);
end
LqInf_res = load('LqInf_results.mat');
X_LqInf = LqInf_res.X_opt;
f1_LqInf = LqInf_res.f1;
f2_LqInf = LqInf_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_LqInf))
f1_s_LqInf(i,:) = (f1_LqInf(i) - f1_g)/(f1_b - f1_g);
f2_s_LqInf(i,:) = (f2_LqInf(i) - f2_g)/(f2_b - f2_g);
end
% combine all results obtained by the Global Criterion method
X_Lq = [X_Lq1; X_Lq2; X_LqInf];
f1_Lq = [f1_Lq1; f1_Lq2; f1_LqInf];
f2_Lq = [f2_Lq1; f2_Lq2; f2_LqInf];
f1_s_Lq = [f1_s_Lq1; f1_s_Lq2; f1_s_LqInf];
f2_s_Lq = [f2_s_Lq1; f2_s_Lq2; f2_s_LqInf];
%% Epsilon Constrained (EC)
% optimizing for drag while constraining volume
EC_res = load('EC_results.mat');
X_EC = EC_res.X;
f1_EC = EC_res.f1;
f2_EC = EC_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_EC))
f1_s_EC(i,:) = (f1_EC(i) - f1_g)/(f1_b - f1_g);
f2_s_EC(i,:) = (f2_EC(i) - f2_g)/(f2_b - f2_g);
end
% optimizing for volume, while constraining drag
EC2_res = load('EC2_results.mat');
X_EC2 = EC2_res.X;
f1_EC2 = EC2_res.f1;
f2_EC2 = EC2_res.f2;
% re-normalize according to full set of optima
for i = 1:max(size(f1_EC2))
f1_s_EC2(i,:) = (f1_EC2(i) - f1_g)/(f1_b - f1_g);
f2_s_EC2(i,:) = (f2_EC2(i) - f2_g)/(f2_b - f2_g);
end
% combine both sets of optima obtained by the epsilon constrained method
X_EC = [X_EC; X_EC2];
其中许多是子函数。在这里,我们解释了在我们的项目演示和报告中显示的结果和图表的复制所需运行的脚本(不包括单调性分析和参数研究)。** 使用加权法、ε-约束法和全局准则法的多目标优化脚本在权重或ε为0/1时包括单目标优化,以及用于计算Lq范数的理想点。运行GridEval.m - 评估跨越变量整个范围的3D立方网格的点。仅保存满足所有约束条件的点,即可行区域。运行PlotGridEval.m - 根据两个目标和设计空间和准则空间中的Lq范数(1、2和Inf)的颜色绘制可行区域的图表。这将花费很长时间。运行weighted_fmincon_Script - 基于内置的MATLAB函数fmincon进行单目标约束优化的自定义加权法多目标优化方法。运行weighted_PenaltyMethod - 基于自定义惩罚法进行单目标约束优化的自定义加权法多目标优化方法,使用内置的MATLAB函数fminunc进行单目标无约束优化。运行weighted_PenaltyMethod2 - 与前一个相同,但使用不同的起始点。运行weighted_AugmentedLagranianMethod - 基于自定义ALM方法进行单目标约束优化的自定义加权法多目标优化方法,使用内置的MATLAB函数fminunc进行无约束优化。运行EpsilonConstrainedMethod_OptDrag - 基于内置的MATLAB函数fmincon进行单目标约束优化的自定义ε-约束法多目标优化方法。在约束体积的同时优化阻力。运行EpsilonConstrainedMethod_OptVolume - 与前一个相同,但在约束阻力的同时优化体积。运行fminimax_script - 使用内置的MATLAB函数fminmax进行多目标优化。运行带q = 1的GlobalCriterionMethod - 基于内置的MATLAB函数fmincon进行单目标约束优化的自定义全局准则法多目标优化方法。运行带q = 2的GlobalCriterionMethod - 与前一个相同,但q = 2。运行带q = Inf的GlobalCriterionMethod - 与前一个相同,但q = Inf。运行Compile_All_Opt - 保存来自不同方法的所有最优值。运行Plot_All_Opt_wColors - 创建所有最优值的图表,使用各种颜色/标记。运行isolate_Pareto - 创建仅显示准则空间中帕累托前沿的图表。运行Plot_Opt_on_Feas - 创建显示设计空间中帕累托前沿点的图表。
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]王宏健,熊伟,WANG,等.基于蚁群优化的AUV全局路径规划研究(英文)[J].Journal of Marine Science and Application, 2009, 8(001):58-64.DOI:CNKI:SUN:HEBD.0.2009-01-013.
[2] Wang H J , Xiong W .基于蚁群优化的AUV全局路径规划研究[J].Journal of Marine ence and Application, 2009, 8(1):58-64.DOI:10.1007/s11804-009-8002-7.
[3]吴亚军,雷江涛,王珲.基于遗传算法的AUV壳体环肋模糊可靠性优化设计[J].鱼雷技术, 2006, 14(3):4.DOI:10.3969/j.issn.1673-1948.2006.03.005.
[4]刘彩云.面向多目标遗传优化的AUV概念设计[D].哈尔滨工程大学[2024-04-09].DOI:CNKI:CDMD:2.1014.132505.























 1273
1273

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








