两轮自平衡车系统的模型构建

1. 两轮自平衡车系统工作原理

   两轮自平衡车的平衡原理来自于倒立摆模型，由于两轮自平衡车的双轮平行布置在车体的左右两端，且载人时重心在双轮轴心正上方，所以它相当于一个倒立摆，是不稳定体，车体总是要向前或向后倾倒。当检测到车体向前倾斜时，内部电机加速旋转产生一个向前的加速度，这个加速度使得在双轮轴心上方的重心向后摆动，这就抵消了车体的向前倾斜，使车体的重心回到两轮中心轴的正上方，从而在竖直方向保持平衡。这一平衡是动态的，为保持车体竖直不倒，必须不断地驱动电机前进或后退，来克服重心偏移现象，保持车体平衡。

                                                               图1 平衡车系统平衡原理图

1. 平衡车系统力学模型

忽略空气阻力后，可以将平衡车抽象成小车和均匀质杆组成的系统，如下图所示：

      

 

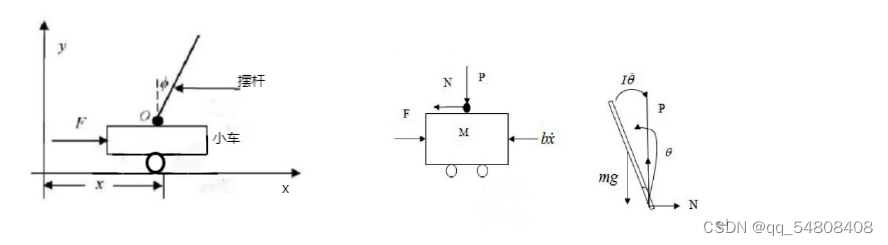
图2 自平衡车系统简图                      图3 小车及摆杆受力分析

其中，M——小车质量      m——摆杆质量     b——小车的摩擦系数

  l——摆杆的转动轴心到质心的长度      I——摆杆惯量

  F——小车受力（内部电机提供）     θ——摆杆与垂直向下方向的夹角

x——小车位移      φ——摆杆与垂直向上方向的夹角

1.分析小车在水平方向所受合力可得：

  2.分析摆杆在水平方向所受合力可得：

3.把（2）式代入（1）式可得系统的第一个运动方程：

4.对摆杆垂直方向受力分析可得：

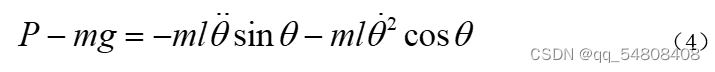
5.把（4）式代入（3）式可得系统的第二个运动方程：

 3.平衡车系统状态空间模型

1. 被控对象的输入力F用u表示，线性化后得到运动方程：

    2.整理后得到系统状态空间表达式：

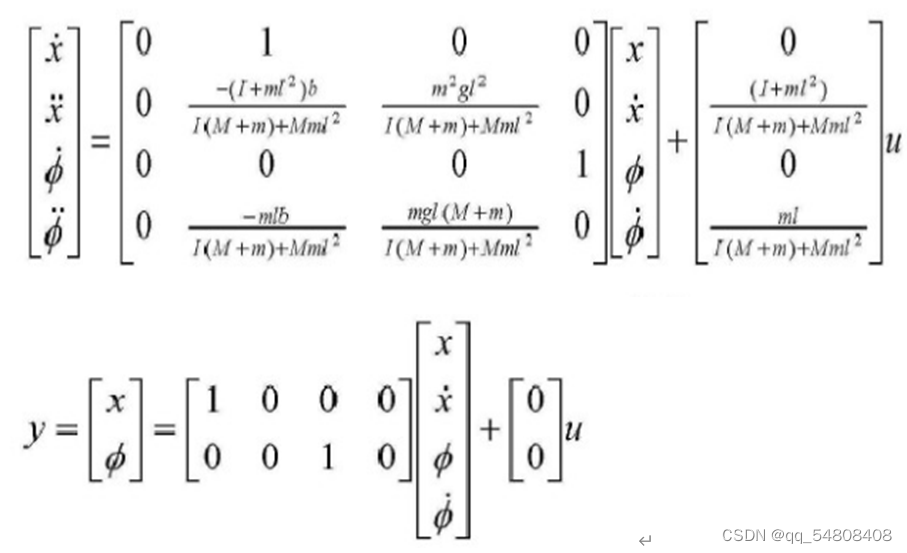 3.各物理量取以下数值，从而得到具体的状态空间模型

                                                                      表1  各物理量取值​​​​​​​

 状态变量：；输入变量：        ；            输出变量：​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​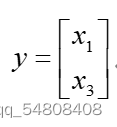

 则状态方程和输出方程：

4.平衡车系统传递函数阵模型

由MATLAB将状态空间模型转换为传递函数模型，得到

（1）y与x1(x)之间的传递函数为：​​​​​​​​​​​​​​

（2）y与x3(φ)之间的传递函数为:  ​​​​​​​     

MATLAB程序附录：

clear;

clc;

syms I m M l b g x fai;

M=1.096;m=0.109;b=0.1;I=0.034;

l=0.25;g=9.8;

t=I*(M+m)+M*m*l^2;

A=[0,1,0,0;

   0,-(I+m*l^2)*b/t,m^2*g*l^2,0;

   0,0,0,1;

   0,-m*l*b/t,m*g*l*(M+m)/t,0;];

B=[0;(I+m*l^2)/t;0;m*l/t;];

C=[1,0,0,0;0,0,1,0;];

D=[0;0];

G_ss=ss(A,B,C,D);%状态空间模型

G_tf=tf(G_ss); %传递函数阵模型