【控制实践——二轮平衡车】【一】运动分析及动力学建模

---

---

系列博客

【控制实践——二轮平衡车】【一】运动分析及动力学建模
【控制实践——二轮平衡车】【二】实物设计和开源结构&代码
【控制实践——二轮平衡车】【三】基于PID的直立控制
【控制实践——二轮平衡车】【四】基于ADRC算法的直立控制
【控制实践——二轮平衡车】【五】转动运动模型及控制方法

前言

之前本科期间也做过二轮平衡车（后简称平衡车）的实践，但当时是抄了别人的开源代码来实现的，用的是最常见的$PID$控制器，参数调试也是玄学调参法，一天一套参数。对于平衡车的理解处于一个非常肤浅的状态（实现出来只能说明具有一定复制粘贴的实践能力而已），更没有系统地对平衡车的运动过程进行详细分析，更别说是控制器相关的设计（博主不是自动化专业的）。
因此！
出于对过去马虎瞒混的弥补，以及对于每年依然有很多的新人会入门平衡车类型的控制实践项目， 想好好地系统地不应付地做一个平衡车控制实践的系列，包括理论、仿真、造实物的调试，会以一个低门槛的，尽可能通俗易懂的形式呈现。
有疑问或发现错误的地方，欢迎提出！

平衡车的物理结构

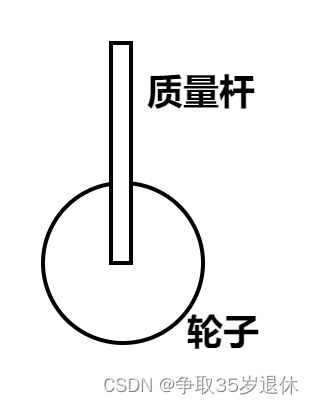
平衡车的物理模型可以简化为质量杆部分和轮子部分，质量杆和轮子的连接可以简化为理想轴承连接的方式。轮子支撑着质量杆，质量杆受到轮子的力并且可以绕着轮子中心转动，
理想轴承连接等于：1.忽略二者之间的转动摩擦 2.二者刚性连接。
忽略地面对轮子的阻力


这是一个重要的理想简化前提，与后面的受力分析有关，如果以不同的方式来简化模型会有不同的结果

平衡车的受力分析

平衡车有两个主要部分，轮子和质量杆，因此我们定义以下的一些物理量：
${\mathbf{m}}_{\mathbf{p}}$：质量杆的质量， $\mathbf{p}$是杆英文$\mathbf{pole}$的首字母；
${\mathbf{m}}_{\mathbf{w}}$：轮子的质量， $\mathbf{w}$是杆英文$\mathbf{wheel}$的首字母；
$\mathbf{l}$：轮子质心到质量杆质心的距离；
$\mathbf{\alpha }$：质量杆质心绕轮子转动的角度，以逆时针为正；
$\mathbf{\omega }$：质量杆质心绕轮子转动的角速度，以逆时针为正；
${\mathbf{x}}_{\mathbf{p}}$：质量杆质心的$\mathbf{X}$轴位移量，以向右为正；
${\mathbf{x}}_{\mathbf{w}}$：轮子质心的$\mathbf{X}$轴位移量，以向右为正；
${\mathbf{y}}_{\mathbf{p}}$：质量杆质心的$\mathbf{Y}$轴位移量，以向上为正；
${\mathbf{F}}_{\mathbf{N}}$：轮子对质量杆竖直向上的支持力；
${\mathbf{F}}_{\mathbf{N}}^{\prime }$：质量杆对轮子竖直向下的反作用力；
${\mathbf{F}}_{\mathbf{T}}$：轮子对质量杆产生的水平方向的力；
${\mathbf{F}}_{\mathbf{T}}^{\prime }$：质量杆对轮子产生的水平方向的反作用力；

轮子

对于轮子而言，它受到的力如下：

其中，$\mathbf{N}$是地面对轮子的支持力。

质量杆

对于质量杆而言，它受到的力如下：

可以得到，
$${\mathbf{F}}_{\mathbf{N}}^{\prime }=-{\mathbf{F}}_{\mathbf{N}}$$
$${\mathbf{F}}_{\mathbf{T}}^{\prime }=-{\mathbf{F}}_{\mathbf{T}}\text{\hspace{1em}(1)}$$

思考时间：为什么轮子对于质量杆的力要分开成XY轴的力，以及二者的合力是否始终沿着质量杆和轮子的轴线？

• 第一个问题是因为后续进行运动分析的时候，就是基于$XY$轴分解进行的，将作用力分解方便后续的分析。
• 第二个问题，二者的合理不始终沿着质量杆和轮子的轴线。这就好比以轮子质心为原点建立一个相对坐标系。而轮子又是会运动的，因此对质量杆的力就包括了切向力和法向力。二者的合力就不一定在轴线上。
  这里涉及到一些惯性力的相关知识。有兴趣的话后期出一篇博客来补充。

平衡车的动力学方程

对于平衡车的轮子部分来说，他的运动范围只有$\mathbf{X}$轴；对于质量杆质心，他的运动范围则有$\mathbf{XY}$两个轴。

轮子的动力学方程

$${\mathbf{m}}_{\mathbf{w}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}={\mathbf{F}}_{\mathbf{T}}^{\prime }\text{\hspace{1em}(2)}$$

质量杆的动力学方程

• $\mathbf{X}$轴方向
  
  由于质量杆是固连在轮子上的，其位移既受到轮子位移${\mathbf{x}}_{\mathbf{w}}$的影响，也受到$\mathbf{\alpha }$，满足以下关系：
  $${\mathbf{x}}_{\mathbf{p}}={\mathbf{x}}_{\mathbf{w}}-\mathbf{l}\cdot \mathbf{sin\alpha }$$
  这里的负号是因为角度的方向判定决定的，翻上去看看定义。
  因此其运动方程为
  $$\begin{gathered} {\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{p}}={\mathbf{F}}_{\mathbf{T}} \\ \Rightarrow {\mathbf{m}}_{\mathbf{p}}({\mathbf{x}}_{\mathbf{w}}-\mathbf{l}\cdot \mathbf{sin\alpha }{)}^{\prime \prime }={\mathbf{F}}_{\mathbf{T}} \\ \Rightarrow {\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}(\stackrel{\cdot }{\mathbf{\alpha }}\mathbf{cos\alpha }{)}^{\prime }={\mathbf{F}}_{\mathbf{T}} \\ \Rightarrow {\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}(\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{cos\alpha }-{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{sin\alpha })={\mathbf{F}}_{\mathbf{T}} \\ \Rightarrow {\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{cos\alpha }+{\mathbf{m}}_{\mathbf{p}}\mathbf{l}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{sin\alpha }={\mathbf{F}}_{\mathbf{T}}\text{\hspace{1em}(3)} \end{gathered}$$
• $\mathbf{Y}$轴方向
  质量杆的$\mathbf{Y}$轴位移就与轮子无关了，满足以下关系
  $${\mathbf{y}}_{\mathbf{p}}=\mathbf{l}\cdot \mathbf{cos\alpha }$$
  则动力学方程为
  $$\begin{gathered} {\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{y}}}_{\mathbf{p}}={\mathbf{F}}_{\mathbf{N}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{g} \\ \to {\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{y}}}_{\mathbf{p}}={\mathbf{F}}_{\mathbf{N}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{g} \\ \to {\mathbf{m}}_{\mathbf{p}}\mathbf{l}(-\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{sin\alpha }-{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{cos\alpha })={\mathbf{F}}_{\mathbf{N}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{g} \\ \to {\mathbf{m}}_{\mathbf{p}}\mathbf{g}-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{sin\alpha }-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{cos\alpha }={\mathbf{F}}_{\mathbf{N}}\text{\hspace{1em}(4)} \end{gathered}$$

平衡车整体位移运动过程

联立上述中公式$1,2,3$，可以得到
$${\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{cos\alpha }+{\mathbf{m}}_{\mathbf{p}}\mathbf{l}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{sin\alpha }=-{\mathbf{m}}_{\mathbf{w}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}$$
整理后得到
$$({\mathbf{m}}_{\mathbf{p}}+{\mathbf{m}}_{\mathbf{w}}){\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}={\mathbf{m}}_{\mathbf{p}}\mathbf{l}\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{cos\alpha }-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{sin\alpha }\text{\hspace{1em}(5)}$$

平衡车整体转动运动过程

• 在进行转动描述时，要引入的是相对坐标系和绝对坐标系的概念。以轮子中心为原点，竖直向上为$Y$轴正方向，水平向右为$X$轴正方向，建立平衡车的相对坐标系。绝对坐标系则是以地球平面建立。
• 在相对坐标系中，质量杆的质心点只围绕轮子中心做转动运动；而在绝对坐标系中，质量杆的质心则是随着轮子的位移做转动和平动的复合运动。通常在描述质量杆质心转动时，是基于相对坐标系进行的，但相对坐标系并非与绝对坐标系相对静止，所以在相对坐标系中描述转动运动时，需要引入惯性力来补充。
  
  其中
  $${\mathbf{F}}_{\mathbf{inertia}}={\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}$$
  满足以下关系
  $$\begin{gathered} \mathbf{J}\stackrel{\cdot \cdot }{\mathbf{\alpha }}={\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }+{\mathbf{F}}_{\mathbf{inertia}}\mathbf{lcos\alpha } \\ \to \mathbf{J}\stackrel{\cdot \cdot }{\mathbf{\alpha }}={\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }+{\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}\mathbf{lcos\alpha }\text{\hspace{1em}(6)} \end{gathered}$$
  其中，$\mathbf{J}$是质量杆绕轮子中心转动的转动惯量。

平衡车运动模型

根据我们的理想简化模型，最终我们得到了两个公式

$$({\mathbf{m}}_{\mathbf{p}}+{\mathbf{m}}_{\mathbf{w}}){\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}={\mathbf{m}}_{\mathbf{p}}\mathbf{l}\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{cos\alpha }-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{sin\alpha }\text{\hspace{1em}(7)}$$
$$\mathbf{J}\stackrel{\cdot \cdot }{\mathbf{\alpha }}={\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }+{\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}\mathbf{lcos\alpha }\text{\hspace{1em}(8)}$$
对于这两个公式而言，是基于不同坐标系下分析得到的。

• 公式（7）描述了惯性系下（以地面为参考系），不同的初始角度${\mathbf{\alpha }}_0$，${\dot{\mathbf{\alpha }}}_0$会如何使轮子运动${\ddot{\mathbf{x}}}_{\mathbf{w}}$
• 公式（8）描述了非惯性系下（以轮子中心为坐标原点，竖直向上为$Y$轴，水平向右为$X$轴），轮子的运动${\ddot{\mathbf{x}}}_{\mathbf{w}}$以及重力的作用${\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }$如何影响角度变化（即平衡车的转动）。

可以看出，在不考虑阻力和无外力作用（轮子不会主动运动）的情况下，角度的运动$\dot{\mathbf{\alpha }}$，$\ddot{\mathbf{\alpha }}$（转动运动）会带动轮子的运动${\ddot{\mathbf{x}}}_{\mathbf{w}}$，而轮子的运动${\ddot{\mathbf{x}}}_{\mathbf{w}}$进而会重新影响角度的运动$\ddot{\mathbf{\alpha }}$（转动运动），形成正反馈的循环，使平衡车加速倒下。

将公式（7）和公式（8）合并后整理得到：
$$(\mathbf{J}-\frac{{\mathbf{m}}_{\mathbf{p}}^2{\mathbf{l}}^2\mathbf{co}{\mathbf{s}}^2\mathbf{\alpha }}{{\mathbf{m}}_{\mathbf{p}}+{\mathbf{m}}_{\mathbf{w}}})\stackrel{\cdot \cdot }{\mathbf{\alpha }}={\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }-\frac{{\mathbf{m}}_{\mathbf{p}}^2{\mathbf{l}}^2\mathbf{sin\alpha cos\alpha }}{{\mathbf{m}}_{\mathbf{p}}+{\mathbf{m}}_{\mathbf{w}}}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\text{\hspace{1em}(9)}$$

平衡车运动仿真

对平衡车系统进行运动仿真，仿真参数如下：
${\mathbf{m}}_{\mathbf{p}}=0.4kg$
${\mathbf{m}}_{\mathbf{w}}=0.1kg$
$\mathbf{l}=0.12m$
$\mathbf{J}=m_p{l}^{2}kg\cdot m^2$
$\mathbf{g}=9.8m^2/s$
初始状态分别为：
${\mathbf{\alpha }}_0=10°$
${\stackrel{\cdot }{\mathbf{\alpha }}}_0=0°/s$
通过调节不同的系统初始状态${\mathbf{\alpha }}_0，{\stackrel{\cdot }{\mathbf{\alpha }}}_0$观察平衡车系统的运动状态。

clear all;
mp = 0.4;
mw = 0.1;
%质量
l = 0.12;
%长度
g = 9.8;
%重力加速度
J = mp*l*l;
%转动惯量
a0 = 10 / 180 * pi;
da0 = 0 / 180 * pi;
x0 = 0;
dx0 = 0;
%初始状态
T = 0.01;
%仿真周期
n = 1000;
%仿真步数
a = zeros(n,1);
da = zeros(n,1);
dda = zeros(n,1);
x = zeros(n,1);
dx = zeros(n,1);
time = zeros(n,1);
coef = zeros(n,1);
a(1) = a0;
da(1) = da0;
k = 0;

for i = 1:1:n-1
    coef(i) = (J - (mp*mp * l*l * cos(a(i))*cos(a(i))) / (mp+mw) );
    
    dda(i+1) = (mp*g*l*sin(a(i)) - ((mp*mp * l*l *sin(a(i))*cos(a(i)))/(mp+mw))  * da(i)*da(i)) / coef(i);
    %角加速度
    da(i+1) = da(i) + dda(i)*T;
    %角速度
    a(i+1) = a(i) + da(i)*T;
    
    time(i+1) = i * T;
    
    if a(i+1) >= pi / 2
        k = i;
        break
    end
end

figure(1);
plot(time(1:k),a(1:k)/pi*180,'r');
legend('a');
xlabel('time/s');
ylabel('°/s')

• 实验结果
  
  可以看出，平衡车在无阻力和外力作用下，将会倒的越来越快，符合公式里正反馈的特性。