基于《高级计算机图形学原理与实践》(西安科技大学)的学习笔记(三)

---

三、自由曲线与曲面

1、基本概念

(1)曲线、曲面的显式、隐式、参数表示
显式：对于一个平面曲线，显式表示一般形式是：y=f(x) 。
隐式：如一个平面曲线方程，表示成 f(x,y)=0 的隐式表示。
参数表示：形如 x=f(t),y=f(t),z=f(t) 的表达式，其中 t
为参数。即曲线上任一点的坐标均表示成给定参数的函数。
(2)参数表示的主要优势
（1）可以满足几何不变性的要求，坐标变换后仍保持几何形状不变；
（2）有更大的自由度来控制曲线、曲面的形状；
（3）参数表示的曲线、曲面可对其参数方程直接进行几何变换；
（4）参数方程中，代数、几何相关和无关的变量是完全分离的，而且对变量个数不限，从而便于用户把低维空间中曲线、曲面扩展到高维空间去；
（5）易于用矢量和矩阵表示几何分量，简化了计算；
（6）规格化的参数变量 t∈[0,1] ，使其相应的几何分量是有界的，而无需重新定义边界。
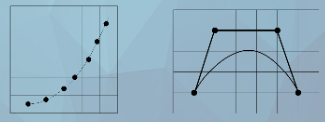
(3)插值与逼近
插值（Interpolation）：当用一组数据点来指定曲线的形状时，曲线精确地通过给定的数据点且形成光滑的曲线，称为曲线的插值。
逼近(Approximation)：当用一组控制点来指定曲线的形状时，曲线被每个控制点所吸引，但并不经过这些控制点，称为曲线的逼近 。
插值与逼近统称为拟合（Fitting）。

(4)光顺与连续性
光顺：通俗含义指曲线的拐点不能太多。对平面曲线而言，相对光顺的条件是：
a）具有二阶几何连续性( )；
b）不存在多余拐点和奇异点；
c）曲率变化较小。
连续性：设计一条复杂曲线时，常常通过多段曲线组合而成，这需要解决曲线段之间如何实现光滑连接的问题，即为连续性问题。

(5)曲线间连接的光滑度的度量有两种
一种是函数的可微性，把组合参数曲线构造成在连接处具有直到 n 阶连续导矢，即 n 阶连续可微，这类光滑度称之为 或 n 阶参数连续性。
另一种称为几何连续性，组合曲线在连接处满足不同于 的某一组约束条件，称为具有 n 阶几何连续性，简记为 。曲线光滑度的两种度量方法并不矛盾， 连续包含在 连续之中。

(6)参数连续性：
C^0，指相邻两段曲线在结合点处具有相同的坐标。
C^1，指相邻两段曲线在结合点处具有相同的一阶导数。
C^2，指相邻两段曲线在结合点处具有相同的一阶导数和二阶导数。

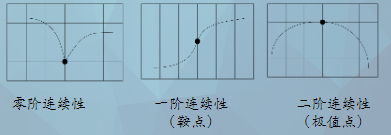
(7)几何连续性:
与参数连续性不同，只要求参数导数成比例，而不是相等！
类似分类：
G^0，指相邻两段曲线在结合点处具有相同的坐标。
G^1，指相邻两段曲线在结合点处的一阶导数成比例 。
G^2，指相邻两段曲线在结合点处的一阶导数和二阶导数成比例，即：曲率一致！ 。

2、参数样条曲线与Hermite

（1）三次参数样条曲线（C2拟合）
特点：
1、使用三次参数多项式来建立
2、曲线通过特定的型值点
3、保持C2连续性
工程选择原因：
1、与高次参数多项式相比，三次参数多项式计算量少且存储稳定
2、更低次的参数多项式难以描述复杂的自由曲线形状
通过n个型值点的连续曲线获得：
1、使用三次参数样条分段插值函数：得到通过两个型值点处的分段三次参数样条曲线
2、对n个型值点，其n-1段曲线之间要平滑连接，能建立n-2个方程组
3、根据边界条件再添加两个方程，综合解出所有系数！
<1>三次参数样条曲线的定义
已知n个型值点Pi(i=1,2…,n)且相邻型值点不重合，若P(t)满足下列条件：
1、型值点Pi在函数P(t)上；
2、P(t)在整个区间[P1,Pn]上二阶连续可导；
3、在每个子区间 [Pi,Pi+1] (i=1,2…,n-1)上，分段函数Pi(t)都是参数t的三次多项式，则称P(t)是过型值点的三次参数样条函数，由它构成的曲线称为三次参数样条曲线。
参数t是相邻型值点之间的弦长，t∈ [0,Li]

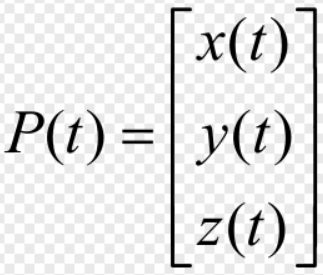
<2>系数求解
第i段三次参数样条曲线的表达式为：

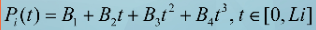
当t=0时，第i段曲线对应于端点Pi：

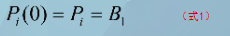
当t=Li时，第i段曲线对应于端点Pi+1：

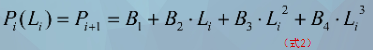
一阶、二阶求导，有：

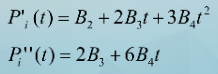
第i段曲线在Pi处的二阶导矢量Mi为：

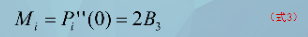
第i段曲线在Pi+1处的二阶导矢量Mi+1为：

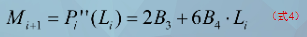
联合（式1-4），可解得：

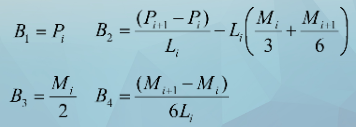
即：分段三次参数样条曲线方程的四个参数B1、B2、B3、B4可由N个二阶导M1—Mn求得。只需求出二阶导M1—Mn即可。
<3>边界条件
利用P(t)一阶导数连续来求解二阶导数矢量Mi,则有：

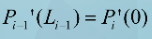
带入参数方程 ，令：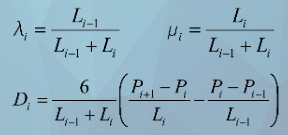
则有：

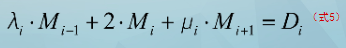
i=2,…，n-1，则可得n-2个方程。
为了求解n个二阶导M1—Mn，还需要两个方程。
两个方程可由起点和终点的两个边界条件获得！

常用的三种边界条件为：
<1>夹持端
给出始端一阶导P’1和终端一阶导P’n，将P’1(0) = P’1 ，代入(式5)：

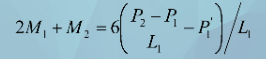
P’n-1(Ln)=P’n，代入(式5)：

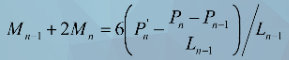
<2>自由端
始端和终端二阶导为0

<3>抛物端
第1段和第n-1段的二阶导为常数

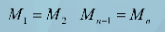
三种边界条件可统一成下面的表达式：

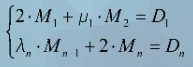
二阶导数矢量Mi求解方程可用三对角阵表示为：

使用追赶法可以求出唯一解，把x,y,z都可看成t的三次样条函数，即:求解三次样条方程.

(2) Hermite样条曲线（C1拟合）
特点：
1、每个曲线段仅依赖于端点的约束，可以局部调整
2、分段三次多项式，由两个端点的坐标和切线来定义

Hermite曲线方程的矩阵形式为:

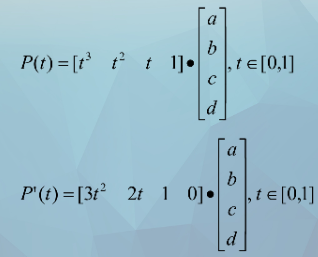
假定型值点Pi和Pi+1之间的曲线段为P(t)，t区间[0,1]，Hermite的边界条件为：

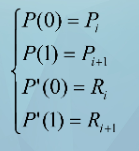
Ri和Ri+1是Pi和Pi+1处的导数值。

两个顶点和两个一阶导边界条件代入可得
Hermite边界条件的矩阵表示：

利用上述方程对多项式系数求解：

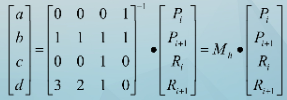
式中Mh称为Hermite矩阵，是边界约束矩阵的逆。
样条曲线P(t)可表示为：

展开成代数形式为：

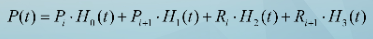
其中H0(t), H1(t), H2(t), H3(t)称为Hermite样条调和函数：
（1）调和了边界约束值，在整个参数方位内产生曲线坐标值！
（2）仅与参数t有关，而与初始条件无关！
（3）调和函数对三个坐标分量x,y,z的作用相同！

Cardinal样条是Hermite样条的变形，其边界条件为：

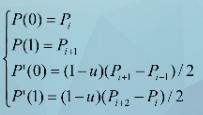
u为一可调参数，称为张力参数，可控制曲线型值点的松紧程度。

三次参数样条曲线、Hermite样条曲线和Cardinal样条曲线的性质和优缺点：
（1）三次参数样条曲线、Hermite样条曲线和Cardinal样条曲线属于拟合范畴。
（2）三次参数样条曲线可以达到二阶参数连续性C2，需要边界条件确定分段插值函数 ；（3）Hermite样条曲线可以达到一阶参数连续性C1，需要每个型值点处的一阶导数作为初始条件；
（4）Cardinal样条曲线是Hermite样条曲线的变形，仅由相邻型值点（两个辅助计算端点）的坐标就可以计算出一阶导数。