复习笔记1——线性回归和逻辑回归
一、机器学习基本概念
1.1 什么是模型
从概率论的角度说,机器学习模型是一个概率分布 P θ ( X ) P_{\theta }(X) Pθ(X) (这里以概率密度函数来代表概率分布)
- X :训练数据
- θ = θ 1 . . . θ n \theta =\theta_{1}...\theta _{n} θ=θ1...θn表示概率分布 P θ P_{\theta } Pθ的 n个参数
机器学习的任务就是求最优参数
θ
t
\theta_{t}
θt ,使得概率分布
P
θ
(
X
)
P_{\theta }(X)
Pθ(X) 最大(即已发生的事实,其对应的概率理应最大)。
θ
t
=
a
r
g
m
a
x
θ
P
θ
X
\theta_{t} =\underset{\theta}{argmax}P_{\theta }X
θt=θargmaxPθX
其中 argmax 函数代表的是取参数使得数据的概率密度最大。
求解最优参数
θ
t
\theta_{t}
θt的过程,我们称之为模型的训练过程( Training ),用来训练这个模型的数据集称之为训练集X( Training Set ),由此得到的模型就可以用来做相应的预测。
1.2 极大似然估计
我们可以把训练集X拆成单条数据的集合X=(X_{1}…X_{n})。每个X的子集为迷你批次。假设单条数据互相独立,上式改写的单条数据乘积可以转为概率对数的求和:
θ
t
=
a
r
g
m
a
x
θ
∏
i
P
θ
X
i
=
a
r
g
m
a
x
θ
∑
i
l
o
g
P
θ
X
i
\theta_{t}=\underset{\theta}{argmax}\prod_{i} P_{\theta }X_{i}=\underset{\theta}{argmax}\sum_{i}log P_{\theta }X_{i}
θt=θargmaxi∏PθXi=θargmaxi∑logPθXi
极大似然估计MLE(Maximum Linklihood Estimation):整体求解上式最优参数 θ t \theta_{t} θt的过程。
1.3为啥使用梯度下降法求解
解方程求解的缺点:
- 机器学习的场景中,训练样本量通常很大,海量的方程通常很难求解。矩阵方式求解,涉及百万维的矩阵运算,对算力。配置要求很高
- 线性回归在对应多元一次方程,尚有解析解。当模型更复杂时(比如不止线性回归),很难找到解析解。即使有,也是特定模型求特定的解析解,无法推广到别的模型
- 解方程需要一次加载全部数据,在数据量很大时,基本做不到(内存会爆)
1.4 梯度下降法本质
- 梯度:在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。
- 梯度向量的意义:从几何意义上讲,梯度就是函数变化增加最快的地方。沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值
- 梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
1.5 梯度下降的算法调优
- 选择合适的学习率(步长),调整每次优化时参数调整的步幅。梯度只是代表下降的方向,真正下降的步幅由学习率控制。太小会很慢,太大会震荡。
- 算法参数的初始值选择。初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值(除非是凸函数)由于有局部最优解的风险,需要多次用不同初始值运行算法
- 归一化。样本不同特征的量纲不一样,会导致迭代很慢(而且结果主要由量纲最大的特征决定)为了减少特征取值的影响,可以对特征数据归一化,也就是对于每个特征x,求出它的期望x¯和标准差std(x),然后转化为:x−x¯/std(x)。这样特征的新期望为0,新方差为1,迭代速度可以大大加快。(也可以防止过拟合)
- 使用合适的优化器(此处不展开)
1.6 归一化的作用
- 使得梯度下降求解时,loss在x的各个维度上的梯度比较一致,各个维度w更新幅度也比较一致,这样可以加快收敛
- 比如逻辑回归中,loss对w导数= ( y ′ − y ) x (y'-y)x (y′−y)x, x = ( x 1 , x 2 . . . x n ) x=(x_{1},x_{2}...x_{n}) x=(x1,x2...xn)。假如 x 1 x_{1} x1的量纲远远大于 x 2 x_{2} x2,则loss对w1的梯度远大于loss对w2的梯度,就会使得更次更新w的时候,在w1方向上的幅度特别大。而x1量纲很大,对w1的变化更敏感,这时候w1剧烈变化会造成loss下降震荡的情况,收敛很慢甚至难以收敛
- 为了使w1和w2对loss下降的贡献一致,我们希望w1更新幅度小,w2更新幅度大,loss对的敏感度一样,这样loss走直线直接下级到最低点。这时,可以设置较高的学习率,减少迭代次数,加快训练。所以需要对x1和x2做归一化处理。
- 消除特征之间量纲的影响,使得不同特征之间具有可比性。否则模型训练结果主要由量纲最大特征的决定。
- 防止过拟合
- 归一化有min-max归一化和零均值归一化。前者是 x = x − x m i n x m a x − x m i n x=\frac{x-x_{min}}{x_{max}-x_{min}} x=xmax−xminx−xmin。后者是 x = x − μ σ x=\frac{x-\mu }{\sigma } x=σx−μ。训练时启用BN,得到参数 μ \mu μ和 σ \sigma σ。预测时不启用BN,采用训练集的训练好的参数进行无偏估计。(待补充)
- 决策树不需要归一化。决策树进行节点分裂主要靠数据集对x的信息增益比来进行。信息增益比跟x是否归一化无关。
1.7 类别特征的表示
- 序号编码:用于处理类别之间有大小关系的数据。比如成绩分为低中高三档等等,存在高>中>低。转换后依然保留了大小关系
- 独热码。在维度很高时存在矩阵稀疏、内存耗费大的问题。可以转为稀疏矩阵,或embedding。
- 二进制编码,本质上是二进制对ID进行哈希映射,得到0/1特征向量,节省空间。
1.8 组合特征
为了提高复杂关系的拟合能力,往往会把一维离散特征两两组合,构成高维组合特征。比如用在推荐系统里面。
1.9 文本表示有哪些模型?
- 词袋模型和n-gram模型
- 主题模型
- 词嵌入和深度学习模型
二、线性回归
2.1为啥线性回归使用mse做损失函数
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KKMusKMb-1637669104119)(./1637488512786.png)]](https://i-blog.csdnimg.cn/blog_migrate/7533c0ae7dbdff90add3acebe18fd8c8.png)
- 损失函数为mse,优化时更容易聚焦到难以优化的点。
- 偏差越大的点,对mse来说,梯度越大,更新幅度就越大。把容易预测的mse降低到一定程度后,再在容易点上优化,收益就变小了。那注意力就会转移到难预测的点上。
- 如果用绝对值误差,收益永远不变,注意力就总在容易的点上了。一直优化容易的点,其他的点没有优化,等于训练集变小了。
- 拿线性回归举例。从全局来看,有些点分布在一条主直线附近,这些点就是容易处理的点;有些点分散的比较远,离主直线也远,就是难以处理的点。数据是否容易处理应从全局来看
- MAE的loss在y=y’这个点没有导数,对梯度下降求解造成障碍
- 以线性回归举例,其模型可以简单地认为是拟合一个函数: y = f θ ( x ) y=f_{\theta }(x) y=fθ(x)。
- 假设噪声符合正态分布 N ( 0 , σ 2 ) N(0,\sigma^{2} ) N(0,σ2),通过极大似然估计求最优参数 θ t \theta_{t} θt。将正态分布公式代入有:
θ t = a r g m a x θ ∑ i l o g P θ X i = a r g m a x θ ∑ i l o g 1 2 π σ e ( f θ ( X i ) − Y i ) 2 2 σ 2 \theta_{t}=\underset{\theta}{argmax}\sum_{i}log P_{\theta }X_{i}=\underset{\theta}{argmax}\sum_{i}log \frac{1}{\sqrt{2\pi }\sigma }e^{\frac{(f_{\theta }(X_{i})-Y_{i})^{2}}{2\sigma ^{2}}} θt=θargmaxi∑logPθXi=θargmaxi∑log2πσ1e2σ2(fθ(Xi)−Yi)2
θ
t
=
a
r
g
m
i
n
θ
∑
i
l
o
g
(
f
θ
(
X
i
)
−
Y
i
)
2
\theta_{t}=\underset{\theta}{argmin}\sum_{i}log (f_{\theta }(X_{i})-Y_{i})^{2}
θt=θargmini∑log(fθ(Xi)−Yi)2
上面argmin中的函数 ,称之为MSE损失函数或者L2模损失函数。
- 如果噪声符合拉普拉斯分布,则有:
P
θ
(
X
i
)
=
e
−
α
∣
f
θ
(
X
i
)
−
Y
i
)
∣
P_{\theta }(X_{i})=e^{-\alpha |f_{\theta }(X_{i})-Y_{i})|}
Pθ(Xi)=e−α∣fθ(Xi)−Yi)∣
θ t = a r g m i n θ ∑ i l o g ∣ ( f θ ( X i ) − Y i ) ∣ \theta_{t}=\underset{\theta}{argmin}\sum_{i}log |(f_{\theta }(X_{i})-Y_{i})| θt=θargmini∑log∣(fθ(Xi)−Yi)∣
上面得到的称之为MAE或者L1模损失函数。
2.2 常见损失函数
2.2.1 MSE和MAE
MAE损失函数:
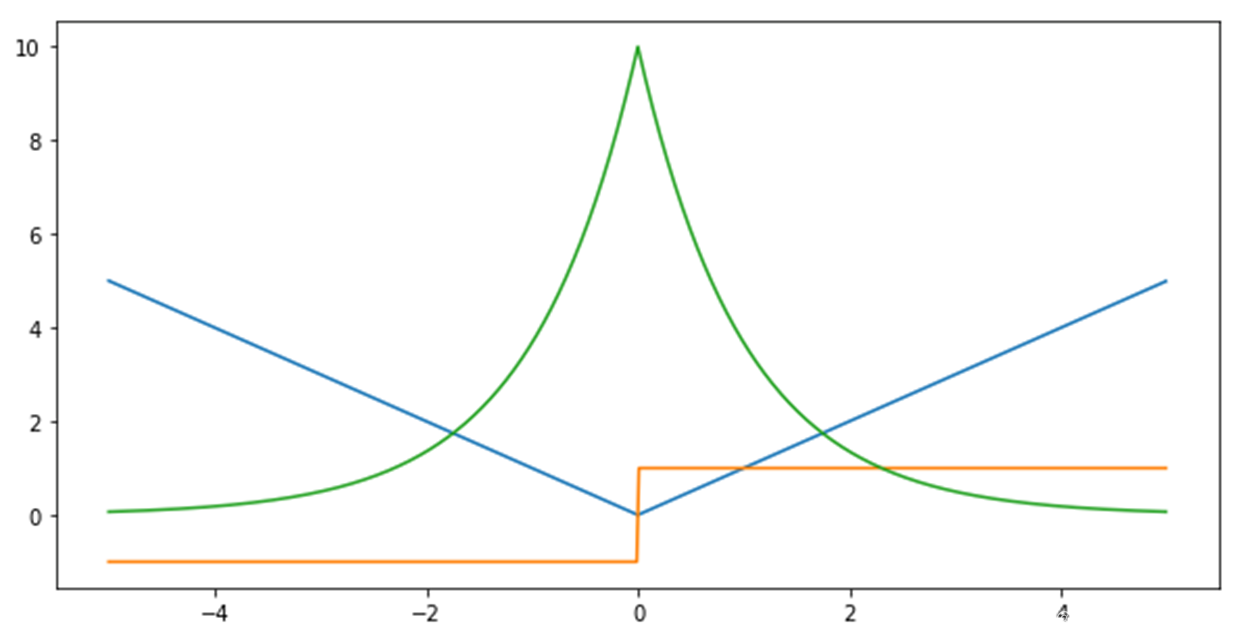
MSE损失函数:
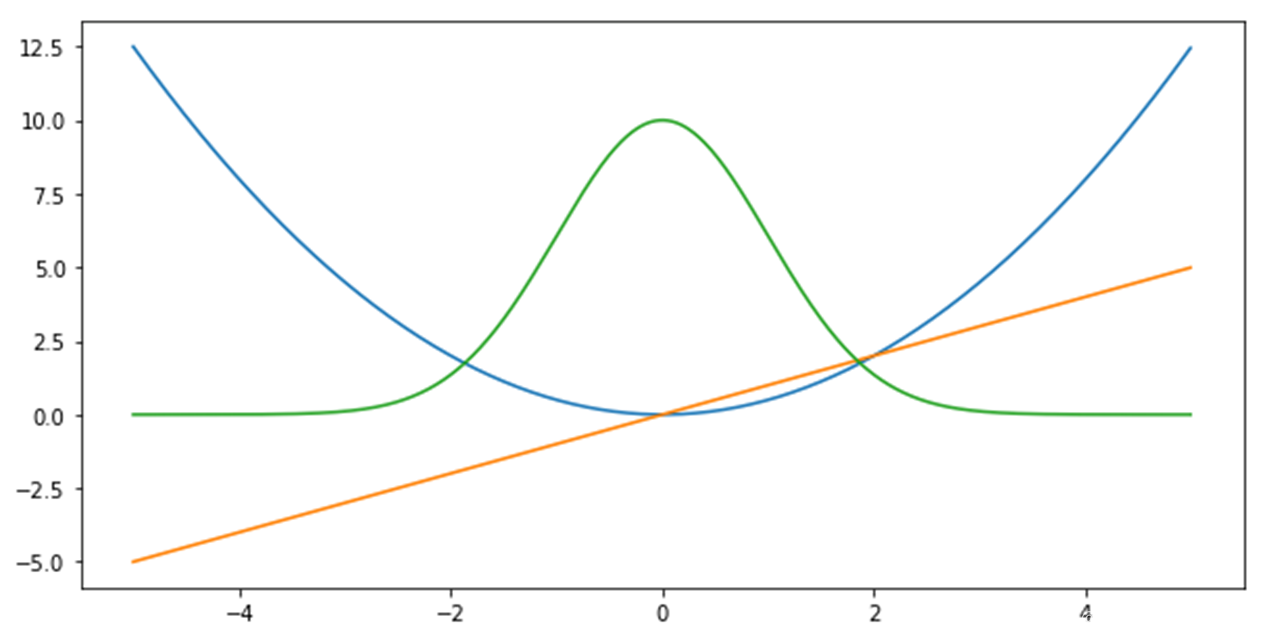
蓝色:损失函数
红色:损失函数导数
绿色:似然估计
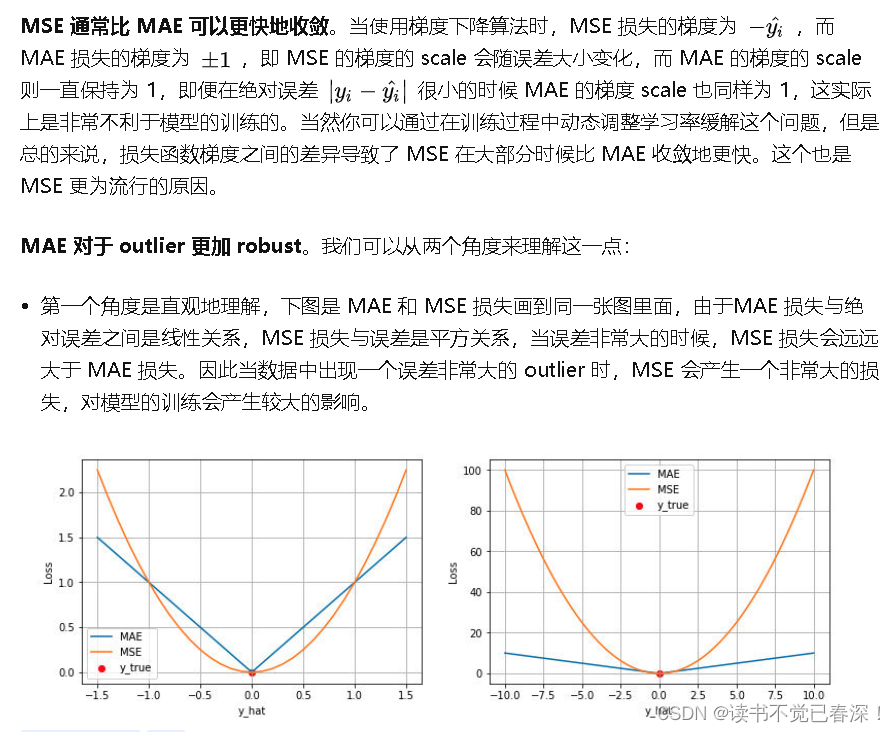
MSE 和 MAE的区别:
- MSE 损失相比 MAE 通常可以更快地收敛,MAE 损失对于 outlier 更加健壮,即更加不易受到 outlier 影响。训练开始时预测误差大,MSE梯度也大,更新更快。到了后期梯度减小,更新慢。MAE来说,即使预测值离真实值很远,梯度也是固定的,不会很大,所以稳定性强。
- MAE在loss=0处不可导(
f
′
(
l
o
s
s
)
∈
[
−
1
,
1
]
f{}'(loss)\in [-1,1]
f′(loss)∈[−1,1]),导数不平滑导致优化到末期可能不那么稳定。
2.2.2 Huber Loss
Huber Loss是一种将 MSE 与 MAE 结合起来,取两者优点的损失函数,也被称作 Smooth Mean Absolute Error Loss 。其原理很简单,就是在误差接近 0 时使用 MSE,误差较大时使用 MAE,公式为:
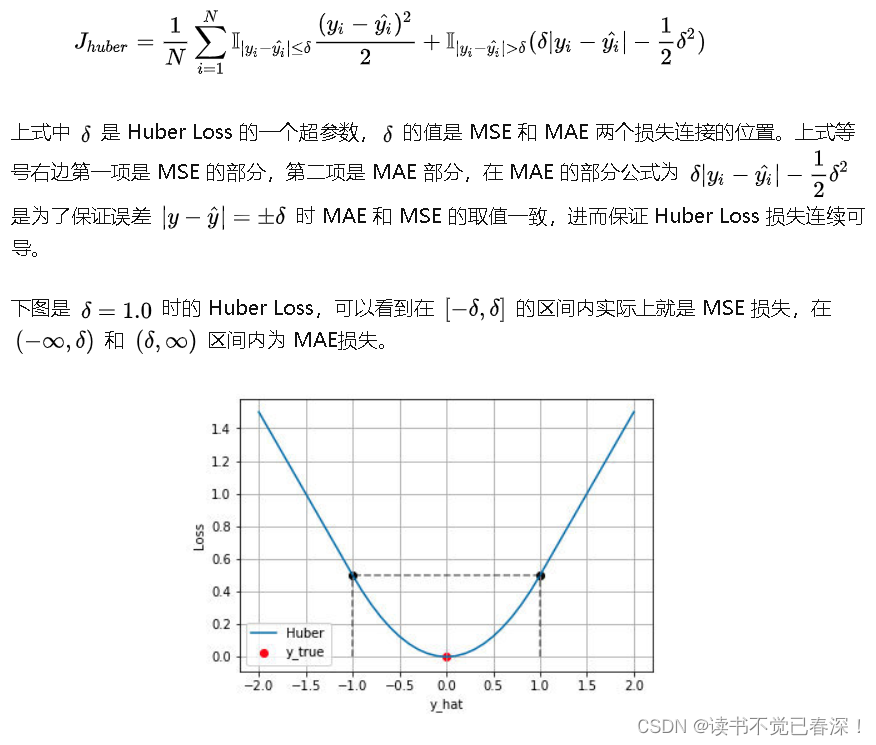
Huber Loss 结合了 MSE和MAE损失,在误差接近0时使用MSE,使损失函数可导并且梯度更加稳定;在误差较大时使用 MAE 可以降低 outlier 的影响,使训练对 outlier 更加健壮。缺点是需要额外地设置一个
δ
\delta
δ超参数(比如取值为1)。
2.2.3 分位数损失 Quantile Loss
分位数回归 Quantile Regression 是一类在实际应用中非常有用的回归算法,通常的回归算法是拟合目标值的期望或者中位数,而分位数回归可以通过给定不同的分位点,拟合目标值的不同分位数。例如我们可以分别拟合出多个分位点,得到一个置信区间,如下图所示(图片来自笔者的一个分位数回归代码 demo Quantile Regression Demo)
其余略
2.2.4 交叉熵损失 Cross Entropy Loss
略,具体看上面链接文章。
2.3 线性回归的抗噪声、抗冗余
噪声对模型的影响:
- 当输入不是一维x而是二维的 [ x 1 , x 2 ] [x_{1,}x_{2}] [x1,x2],其中 x 2 x_{2} x2, 随机产生。 y = w 1 x 1 + w 2 x 2 + w 0 y=w_{1} x_{1}+w_{2} x_{2}+w_{0} y=w1x1+w2x2+w0。训练结果: w 2 = − 0.3424 w_{2}=-0.3424 w2=−0.3424,趋近于0,即对结果没有太大影响。说明线性回归有一定的抗噪声能力。无关的随机输入不会对模型效果产生影响。
- 单纯增加噪声,在样本量足够时,不会对最终结果产生很大影响,只是会增大运算量(所以过拟合时,增大训练样本数量,除了模型见多识广,还可以使噪声的影响趋近于0)
- 样本量不够时,特征中的噪声会对模型产生误导,使模型效果变差
冗余对模型的影响:
- 如果特征出现了冗余,权重会分散到各个冗余维度上。所以不能单纯将权重作为衡量特征重要性的指标。特征权重低,有可能是不重要,有可能是冗余造成的权重稀释。
- 只有在完全线性无关,没有冗余的时候 w i w_{i} wi才是 x i x_{i} xi的权重。而实际过程中并不能完全抗冗余,故 w i w_{i} wi不能完全当做权重来看。对于 y = w 1 x 1 + w 2 x 2 + w 0 y=w_{1} x_{1}+w_{2} x_{2}+w_{0} y=w1x1+w2x2+w0,如果 w 2 w_{2} w2最小,此时并不能拿掉 w 2 x 2 w_{2} x_{2} w2x2项;来降维,因为存在信息分散的情况。
- 噪声是真的没有信息量,而特征重复是因为信息冗余而没有信息量,重复提取特征不会对信息带来任何增量。纯加噪声对mse没有任何伤害,纯加冗余对mse没有帮助,故可以降低提取特征的技巧。
2.4 正则化和过拟合
正则化主要是为了抑制模型的复杂度,防止过拟合,防止w数值过大模型过硬。如果是平滑任务可以使用正则项,根据经验和数据量调整正则化系数。非平滑任务,是否适用机器学习都需要商酌。
训练中,模型分布会逐渐趋向训练集分布。如果没有限制参数的范围,loss会一直减少,模型会不断拟合训练集中所有的点,产生过拟合。
- 从限制参数选择范围的角度来说,为了减小过拟合趋势,可以认为假设参数满足一定的分布,减小参数的选择范围。这种人为选择的参数分布称之为先验分布。范数:向量的长度或距离
-
假设参数的选择服从正态分布,可以得到:
θ t = a r g m a x θ ∑ i l o g P θ ( X i ∣ θ ) P ( θ ) = a r g m i n ∑ i l o g ( f θ ( X i ) − Y i ) 2 + α 2 ∣ ∣ θ ∣ ∣ 2 \theta _{t}=\underset{\theta}{argmax}\sum_{i}log P_{\theta }(X_{i}|\theta)P(\theta)=argmin\sum_{i}log (f_{\theta }(X_{i})-Y_{i})^{2}+\frac{\alpha }{2}||\theta ||^{2} θt=θargmaxi∑logPθ(Xi∣θ)P(θ)=argmini∑log(fθ(Xi)−Yi)2+2α∣∣θ∣∣2
后一项为L2正则化系数,是所有参数的平方和乘以系数 α \alpha α(参数向量的L2范数,对应欧氏距离)。其中, α = σ 2 σ 1 2 \alpha =\frac{\sigma ^{2}}{\sigma _{1}^{2}} α=σ12σ2。正则化系数越大,正则化效果越强,模型更偏向欠拟合区域。反之偏向过拟合区域。调节正则化系数就可以调节模型的过拟合情况。 -
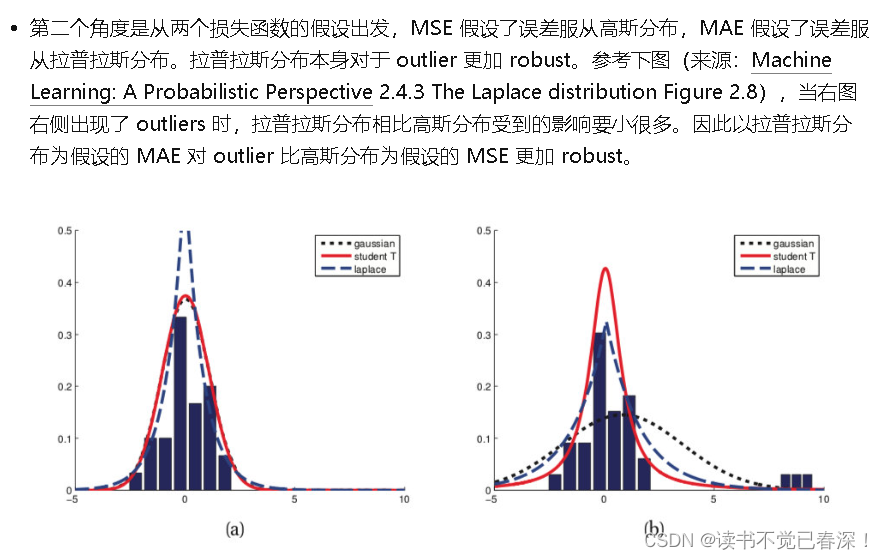
假设参数的选择服从拉普拉斯分布,最后会得到L1正则化项(参数向量的L1范数,对应曼哈顿距离),即所有参数绝对值之和。
θ t = a r g m a x θ ∑ i l o g P θ ( X i ∣ θ ) P ( θ ) = a r g m i n ∑ i l o g ( f θ ( X i ) − Y i ) 2 + α ∣ ∣ θ ∣ ∣ 1 \theta _{t}=\underset{\theta}{argmax}\sum_{i}log P_{\theta }(X_{i}|\theta)P(\theta)=argmin\sum_{i}log (f_{\theta }(X_{i})-Y_{i})^{2}+{\alpha }||\theta ||_{1} θt=θargmaxi∑logPθ(Xi∣θ)P(θ)=argmini∑log(fθ(Xi)−Yi)2+α∣∣θ∣∣1
- 从期望风险、经验风险和结构风险的角度来说:
- 期望风险是模型f(x)关于联合分布P(x,y)的平均损失,学习的目标就是选择期望风险最小的模型,但是联合分布P(x,y)未知,期望损失无法直接求出。所以我们只能求训练集数据的平均损失,称为经验风险或经验损失。我们只能用经验风险来估计期望风险。但是训练样本数目有限,这样直接估计会有偏差,会产生过拟合(模型实际只是拟合训练集),所以需要进行一定的矫正。
- 当模型是条件概率分布,损失函数是对数损失函数的时候,经验风险最小化等价于极大似然估计。
- 结构风险最小化就是为了防止过拟合提出的,结构风险在经验风险的基础上加入代表模型复杂的正则项,或者说是惩罚项,所以结构风险最小化等价于正则化。
- 经验风险是局部概念,针对训练样本损失函数,可以求出。期望风险是全局概念,针对未知测试样本的损失函数,无法求得。结构风险是二者的折中,是经验风险与正则化的加和。
- 当模型是条件概率分布,损失函数是对数损失函数的时候,模型的复杂度由模型的先验概率表示时,结构风险最小化等价于最大后验概率。(如贝叶斯估计的最大后验概率估计)
- 从限制w过大的方面说明:(参数过大包含参数数量过多和数值过大)
- w过大会放大d值,逻辑回归的预测值都接近0或1,模型输出区分度不高,模型太硬,难以选取合适的阈值
- 逻辑回归导数进入饱和区,学习困难
- x的轻微变化乘以一个较大的w,输出变化大。即模型太敏感,不够稳定。我们处理的任务往往是有平滑性的,输入的微小变化不会影响结果的巨大变化。而预测质数这种,数值变化小,结果变化很大的非平滑任务,机器学习的效果很差。
归根结底一句话,训练集数据分布无法完全代表真实数据的分布,所以需要进行调整。正则化项中不包含
w
0
w_{0}
w0,因为对输入x不产生影响。使用L2正则化的逻辑回归称为岭回归。
防止过拟合的其它方法:
- 提前停止:验证集loss不再下降反而上升,可以判断是过拟合,提前停止训练
- dropout:把神经元按照一定概率置为零
- 权重衰减Weight Decay
- 归一化(使异常点不那么异常,待补充)
这些方法本质都是减小参数的变化空间,缩小模型的表示范围,达到训练模型又较好泛化的效果。 - 集成学习:集合多个模型的结果,降低单一模型的过拟合风险
2.5 欠拟合的解决办法
- 添加新特征:现有特征与标签相关性不强的时候,模型容易欠拟合。或者说数据处理不当,比如有一类图片处理有问题。
- 用复杂一点的模型。比如TF-IDF+朴素贝叶斯做文本分类的效果比较差,考虑用复杂一点的模型
- 减小正则化项系数
2.6 泛化误差上界
- 模型对未知数据的误差即为泛化误差,反映了学习方法的泛化能力。泛化误差就是模型的期望风险。
- 学习方法的泛化能力往往通过研究泛化误差的概率上界来进行,称为泛化误差上界。它是样本容量的函数,样本趋近于+∞时,泛化误差上界趋近于0。也是假设空间(输入空间到输出空间映射的集合,包含所有可能的条件概率分布或决策函数)容量的函数,容量越大,模型越南学习,泛化误差上界越大。泛化误差≤训练误差+e。
三、逻辑回归
3.1 概率论
3.1.1 熵
信息论的核心思想是量化数据中的信息内容。
在信息论中,该数值被称为分布
P
P
P的熵(entropy)。可以通过以下方程得到:
H
[
P
]
=
∑
j
−
P
(
j
)
log
P
(
j
)
.
H[P] = \sum_j - P(j) \log P(j).
H[P]=j∑−P(j)logP(j).
信息论的基本定理之一指出,为了对从分布
p
p
p中随机抽取的数据进行编码,我们至少需要
H
[
P
]
H[P]
H[P]“纳特(nat)”对其进行编码。“纳特”相当于比特(bit),但是对数底为
e
e
e而不是2。因此,一个纳特是
1
log
(
2
)
≈
1.44
\frac{1}{\log(2)} \approx 1.44
log(2)1≈1.44比特。
3.1.2 信息量
压缩与预测有什么关系呢?想象一下,我们有一个要压缩的数据流。如果我们很容易预测下一个数据,那么这个数据就很容易压缩。
为什么呢?
举一个极端的例子,假如数据流中的每个数据完全相同,这会是一个非常无聊的数据流。由于它们总是相同的,我们总是知道下一个数据是什么。所以,为了传递数据流的内容,我们不必传输任何信息。也就是说,“下一个数据是xx”这个事件毫无信息量。
但是,如果我们不能完全预测每一个事件,那么我们有时可能会感到"惊异"。克劳德·香农决定用信息量
log
1
P
(
j
)
=
−
log
P
(
j
)
\log \frac{1}{P(j)} = -\log P(j)
logP(j)1=−logP(j)来量化这种惊异程度。在观察一个事件
j
j
j时,并赋予它(主观)概率
P
(
j
)
P(j)
P(j)。当我们赋予一个事件较低的概率时,我们的惊异会更大,该事件的信息量也就更大。
在 3.1.1中定义的熵,是当分配的概率真正匹配数据生成过程时的信息量的期望。
3.2为何逻辑回归使用交叉熵为损失函数
重新审视交叉熵
如果把熵
H
(
P
)
H(P)
H(P)想象为“知道真实概率的人所经历的惊异程度” ,那么什么是交叉熵?
交叉熵从
P
P
P到
Q
Q
Q,记为
H
(
P
,
Q
)
H(P, Q)
H(P,Q)。你可以把交叉熵想象为“主观概率为
Q
Q
Q的观察者在看到根据概率
P
P
P生成的数据时的预期惊异”。
当
P
=
Q
P=Q
P=Q时,交叉熵达到最低。在这种情况下,从
P
P
P到
Q
Q
Q的交叉熵是
H
(
P
,
P
)
=
H
(
P
)
H(P, P)= H(P)
H(P,P)=H(P)。
简而言之,我们可以从两方面来考虑交叉熵分类目标:
- 最大化观测数据的似然;
- 最小化传达标签所需的惊异。
- 从KL散度去理解:
相对熵又称KL散度,如果对于同一个随机变量x 有两个单独的概率分布p(x)和 q(x),可以使用相对熵来衡量这两个分布的差异:
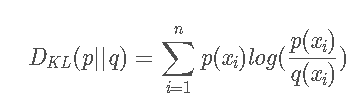
注: D K L D_{KL} DKL越小,表示p(x)和q(x)的分布越近。
在机器学习中,往往用p(x)用来描述真实分布,q(x)用来描述模型预测的分布。计算损失,理应使用相对熵来计算概率分布的差异,然而由相对熵推导出的结果看:

相
对
熵
=
交
叉
熵
−
信
息
熵
相对熵=交叉熵−信息熵
相对熵=交叉熵−信息熵
由于信息熵描述的是消除 p (即真实分布) 的不确定性所需信息量的度量,所以其值应该是最小的、固定的。那么:优化减小相对熵也就是优化交叉熵,所以在机器学习中使用交叉熵就可以了。
考虑y=0和y=1的情况,最终: L o s s = − 1 n ∑ i = 1 n y i l o g ( f i ) + ( 1 − y i ) l o g ( 1 − f i ) Loss=\frac{-1}{n}\sum_{i=1}^{n}y_{i}log(f_{i})+(1-y_{i})log(1-f_{i}) Loss=n−1i=1∑nyilog(fi)+(1−yi)log(1−fi)
- 从极大似然估计的角度可以推导出交叉熵
逻辑回归假设样本服从伯努利分布(0-1分布)设x为特征向量,y为真实的标签。y_是预测值,得出:
y = 1 : P ( y ∣ x ) = y ′ y=1:P(y|x)=y' y=1:P(y∣x)=y′
y = 0 : P ( y ∣ x ) = 1 − y ′ y=0:P(y|x)=1-y' y=0:P(y∣x)=1−y′
两个合并起来写为:
P ( y ∣ x ) = y ′ y ( 1 − y ′ ) 1 − y P(y|x)=y'^{y}(1-y')^{1-y} P(y∣x)=y′y(1−y′)1−y
这个式子被称为似然函数,意思是预测结果靠近或者接近真实值的程度。我们求解模型的目的就是最大化似然函数。为了方便求解,把似然函数两边取对数:
l o g P ( y ∣ x ) = y l o g y ′ + ( 1 − y ) l o g ( 1 − y ′ ) = − L o s s ( y , y ′ ) logP(y|x)=ylogy'+(1-y)log(1-y')=-Loss(y,y') logP(y∣x)=ylogy′+(1−y)log(1−y′)=−Loss(y,y′)
上式中的大写L就是代表损失函数,最大化似然函数也就是最小化损失函数。 LR的损失函数为: 负的对数损失函数
- 从求导的方向考虑(再找时间推一遍)
在梯度计算层面上,交叉熵对参数的偏导不含对sigmoid函数的求导,而均方误差(MSE)等其他则含有sigmoid函数的偏导项。大家知道sigmoid的值很小或者很大时梯度几乎为零,参数几乎就不更新了,w在局部极小值就会停下。这会使得梯度下降算法无法取得有效进展,交叉熵则避免了这一问题。
推导见《速通机器学习》P35
3.3 上采样和下采样
正负样本差异过大时,比如负样本数远大于正样本数,会造成:
- loss主要由负样本决定,w受负样本影响大。比如主要全部预测为负样本,就可以得到一个很小的loss。而我们真正关心的正样本都预测错了
- 训练时每个样本对参数w产生影响,会使分类线往远离自己的方向推来提高预测的概率。如果负类远大于正类,负类力道太大,分类线不再位于两类中间,而是挨着甚至超过正样本,使正样本预测错误,模型泛化能力差。
为了解决样本不平衡的影响,可以采用上采样或下采样:
- 上采样:复制正类样本,使正负样本数量相同
- 下采样:随机抽取部分负类样本为负样本,使正负样本数量相同
实际中采用上采样,保证数据多样性。下采样抛弃部分负样本,数据量减少。正负样本差别特别大的时候,可以两个一起使用
3.4 为什么逻辑函数是这个公式
逻辑函数是从正态分布和贝叶斯公式导出来的。则可以取男性为正样本y=1,女性为负样本y=0。输入一个身高170,如何判断性别。
3.5 线性不可分问题
增加特征维度,对特征进行扩充。线性可分的情况下,loss没有极小值,可以一直减小(所以会加正则项)。线性不可分的情况下,loss是一个抛物线,存在极小值。(所以逻辑回归的loss都有极小值)
四、如何理解AUC
参考:如何理解AUC?
- 正确率指标缺点:容易被类别不平衡所影响(受大类影响)。容易被阈值所影响
- 准确率和召回率缺点:单独看一类预测结果的指标,但被阈值所影响(互相矛盾)
- ROC曲线 和auc值:真正反映了模型的能力,表达了正负样本分数的区分度
- AUC缺点1:仅保序。P=0.51,N=0.49和P=0.8,N=0.2的结果是一样的。但是前一种分类结果区分度不够,稍有扰动就会出错。
- AUC缺点2:无法区分同类别的得分大小,无法区分正样本中像和更像的区别。样本描述情况不够。(只是定性,不够定量)
4.1、关于ROC的几个概念
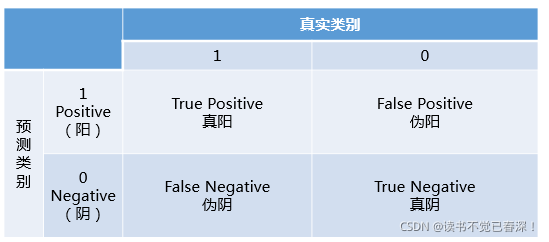
混淆矩阵中有着Positive、Negative、True、False的概念,其意义如下:称预测类别为1的为Positive(阳性),预测类别为0的为Negative(阴性)。预测正确的为True(真),预测错误的为False(伪)。对上述概念进行组合,就产生了如下的混淆矩阵:
| 名称 | 公式 | 意义 |
|---|---|---|
| 准确率(正确率) | a c c u r a c y = ( T P + T N ) ( T P + T N + F P + F N ) \mathbf{accuracy=\frac{(TP+TN)}{(TP+TN+FP+FN)}} accuracy=(TP+TN+FP+FN)(TP+TN) | 所有样本预测对的比例 |
| 精准率-查准率PPV | P r e c i s i o n = T P ( T P + F P ) \mathbf{Precision=\frac{TP}{(TP+FP)}} Precision=(TP+FP)TP | 所有被预测为1的样本中正样本的概率 |
| 召回率-真阳率-查全率-TPR | R e c a l l = T P ( T P + F N ) \mathbf {Recall= \frac{TP}{(TP+FN)}} Recall=(TP+FN)TP | 正样本中被预为1的概率(正样本预测对的比例) |
| 特异度-真阴率 | T N R = T N ( T N + F P ) \mathbf {TNR= \frac{TN}{(TN+FP)}} TNR=(TN+FP)TN | 负样本中被预为0的概率(负样本预测对的比例) |
| 假阳率 | F P R = T P ( T N + F P ) = 1 − 特 异 度 \mathbf {FPR=\frac{TP}{(TN+FP)}=1-特异度} FPR=(TN+FP)TP=1−特异度 | 负样本中预测为1的概率 |
| f1-score | 2 1 / P r e c i s i o n + 1 / R e c a l l = 2 × P r e c i s i o n × R e a c l l P r e c i s i o n + R e c a l l \mathbf {\frac{2}{1/Precision+1/Recall}=2\times \frac{Precision\times Reacll}{Precision+Recall}} 1/Precision+1/Recall2=2×Precision+RecallPrecision×Reacll | 精准率和召回率的平衡点 |
| P-R曲线 | 横轴召回率(真阳率),纵轴精准率 | 刻画精准率和召回率之间的关系 |
| ROC | 横轴假阳率,纵轴真阳率,遍历所有阈值点得到的曲线 | |
| AUC | Area Under ROC Curve,也就是ROC曲线下面的面积 | 同时考虑分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。 |
- 准确率在样本不平衡问题时,其度量效果会产生问题。比如在一个总样本中,1类样本占90%,0类样本占10%,样本严重不平衡,此时我们只需要将全部样本预测为1即可得到高达90%的准确率。
- AUC:同时考虑分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。
- AUC:遍历阈值得到真阳率和假阳率,再与(0,0)、(1,1)连接的曲线下面积。
- 如y=x时,AUC=0.5。
- 全部预测为负类时,真阳率假阳率为0,所有ROC点都为(0,0),连接(0,0)…、(1,1)得AUC=0.5。
- 所有正例概率大于所有负例概率时,所有ROC=(0,1)。连接(0,0)、(0,1)…、(1,1)得AUC=1。
4.2 P-R曲线
-
精准率和召回率是一对矛盾的度量,阈值升高,精准率升高,召回率降低。电商场景中希望把更多商品推送给用户,召回率会提高;金融风险中,银行判断违规客户要求精准度高。P-R曲线刻画精准率和召回率之间的关系,
-
以精准率为y轴,以召回率为x轴,可以画出下面的P-R曲线。两者的关系可以用一个P-R图来展示:
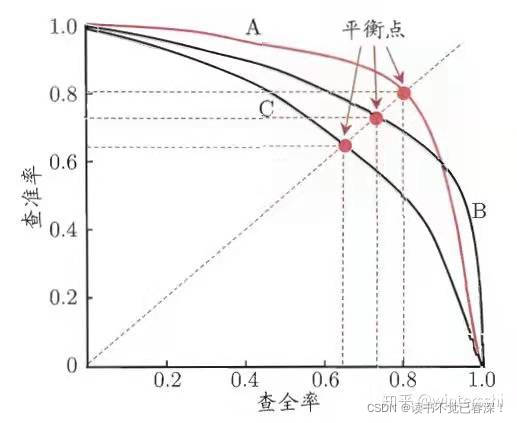
如何理解P-R(查准率-查全率)这条曲线?
拿逻辑回归举例,逻辑回归的输出是一个0到1之间的概率数字。对于阈值为0.5的情况下,我们可以得到相应的一对查准率和查全率。遍历0到1之间所有的阈值,而每个阈值下都对应着一对查准率和查全率,从而我们就得到了这条曲线。
如何找到最好的阈值点呢?这两个指标是一对矛盾体,无法做到双高。图中明显看到,如果其中一个非常高,另一个肯定会非常低。选取合适的阈值点要根据实际需求,比如我们想要高的查全率,那么我们就会牺牲一些查准率,在保证查全率最高的情况下,查准率也不那么低。
4.3 F1分数
通常情况下,精确率和召回率会随着阈值的变化而变化,且互相矛盾。如果想要找到二者之间的一个平衡点,我们就需要一个新的指标:F1分数。F1分数同时考虑了查准率和查全率,让二者同时达到最高。通过选取最高的F1来确定分类阈值,F1公式如下:
1
F
1
=
1
P
r
e
c
i
s
i
o
n
+
1
R
e
c
a
l
l
\frac{1}{F1}=\frac{1}{Precision}+\frac{1}{Recall}
F11=Precision1+Recall1
4.4、ROC/AUC
4.4.1 ROC定义
AUC 的全称是 Area Under ROC Curve,也就是ROC曲线下面的面积。
ROC曲线的横轴是FPR,即False Positive(伪阳率),;纵轴是TPRate,即True Positive Rate(真阳率)。不同的阈值会影响得到的TPRate,FPRate,如果阈值取0.5,那么我们就得到了与之前一样的混淆矩阵。
遍历不同的阈值描点得到整条ROC曲线:依次使用所有预测值作为阈值,得到一系列TPRate,FPRate,描点。然后求面积,即可得到AUC。
当二者相等时,即y=x,如下图:
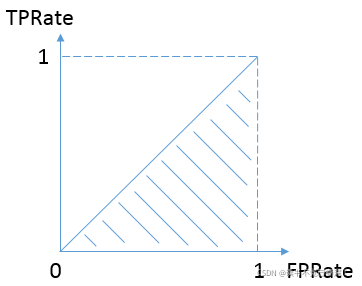
表示的意义是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的。和抛硬币没什么区别。AUC的最小值为0.5
而我们希望分类器达到的效果是:分类器预测正样本为1的概率,要大负样本被预测为1的概率,即真阳率大于假阳率,y>x。因此大部分的ROC曲线长成下面这个样子:
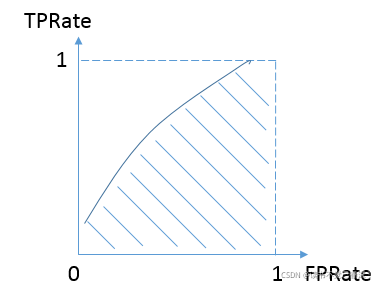
最理想的情况下,既没有真实类别为1而错分为0的样本——TPRate一直为1,也没有真实类别为0而错分为1的样本——FP rate一直为0,AUC为1,这便是AUC的极大值。(在图上是连接(1,1)这个点的正方形)
4.4.2 举例说明ROC/AUC
举个简单的例子。首先对于硬分类器(例如SVM,NB),预测类别为离散标签,对于8个样本的预测情况如下:

得到混淆矩阵如下:
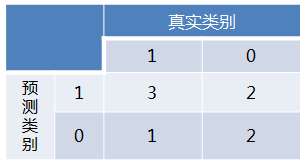
进而算得TPRate=3/4,FPRate=2/4,连接(0,0)(0.5,0.75)和(1,1)三点得到ROC曲线:
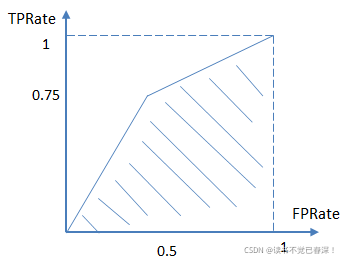
最终得到AUC为0.625。取另一个阈值得到新ROC上的点,可以再次连起来得到新的AUC。
对于LR等预测类别为概率的分类器,依然用上述例子,假设预测结果如下:

这时,需要设置阈值来得到混淆矩阵,遍历不同的阈值描点得到整条ROC曲线,,然后求得AUC。
4.4.3AUC的优势
AUC的计算方法同时考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。
例如在反欺诈场景,设欺诈类样本为正例,正例占比很少(假设0.1%),如果使用准确率评估,把所有的样本预测为负例,便可以获得99.9%的准确率。但是如果使用AUC,把所有样本预测为负例,TPRate和FPRate同时为0(没有Positive),与(0,0) (1,1)连接,得出AUC仅为0.5,成功规避了样本不均匀带来的问题。
4.5、AUC的计算公式
AUC其实也可以这样理解:随机从正样本和负样本中各选一个,分类器对于该正样本打分大于该负样本打分的概率。
假设数据集一共有M个正样本,N个负样本,预测值也就是M+N个。我们将所有样本按照预测值进行从小到大排序,并排序编号由1到M+N。
4.6、ROC/AUC代码
二分类
def binary_class_auc(X, y, model):
param X: 特征
param y: 标签
param model: 训练好的模型
return: roc曲线图
'''
from sklearn import metrics
y_score = model.predict_proba(X)
fpr, tpr, threshold = metrics.roc_curve(y, y_score[:,1])
roc_auc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, label='AUC = %0.3f' % roc_auc)
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r', alpha=.8)
plt.legend(loc='lower right')
plt.show()
binary_class_auc(x_test, y_test, model)
多分类
def mul_class_auc(X, y, model, class_number):
param X: 特征
param y: 标签
param model: 训练好的模型
param class_number: 分类数
return: roc曲线图
'''
from sklearn import metrics
y_score = model.predict_proba(X)
y_one_hot = label_binarize(y, np.arange(class_number))
fpr, tpr, threshold = metrics.roc_curve(y_one_hot.ravel(), y_score.ravel())
roc_auc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, label='AUC = %0.3f' % roc_auc)
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r', alpha=.8)
plt.legend(loc='lower right')
plt.show()
mul_class_auc(x_test, y_test, model, 3)
4.7 sklearn.metrics
模块包括评分函数、性能指标和成对度量和距离计算。
导入:from sklearn import metrics
分类指标
accuracy_score(y_true, y_pre)#精度
log_loss(y_true, y_pred, eps=1e-15, normalize=True, sample_weight=None, labels=None)交叉熵损失函数
auc(x, y, reorder=False)
ROC曲线下的面积;较大的AUC代表了较好的performance。
AUC:roc_auc_score(y_true, y_score, average=‘macro’, sample_weight=None)
f1_score(y_true, y_pred, labels=None, pos_label=1, average=‘binary’, sample_weight=None) F1值
precision_score(y_true, y_pred, labels=None, pos_label=1, average=‘binary’,) 查准率
recall_score(y_true, y_pred, labels=None, pos_label=1, average=‘binary’, sample_weight=None) 查全率
roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=True)
计算ROC曲线的横纵坐标值,TPR,FPR
TPR = TP/(TP+FN) = recall(真正例率,敏感度)
FPR = FP/(FP+TN)(假正例率,1-特异性)
classification_report(y_true, y_pred)#分类结果分析汇总
回归指标
explained_variance_score(y_true, y_pred, sample_weight=None, multioutput=‘uniform_average’)
回归方差(反应自变量与因变量之间的相关程度)
mean_absolute_error(y_true, y_pred, sample_weight=None, multioutput=‘uniform_average’)
平均绝对误差MAE
mean_squared_error(y_true, y_pred, sample_weight=None, multioutput=‘uniform_average’) #均方差MSE
median_absolute_error(y_true, y_pred)
中值绝对误差
r2_score(y_true, y_pred, sample_weight=None, multioutput=‘uniform_average’) #R平方值
五、度量学习
- 传统模型都是一个输入对应一个输出。度量学习是一种空间映射方法,通过神经网络将数据(文字、图片等)映射至共同向量空间。通过数据的向量化,计算不同的样本是否匹配(计算特征向量距离的远近)。
- 向量化不是根据数据提取特征向量,而是根据任务驱动来提取特征。
- 正样本是人工标注的匹配样本,往往是极少数的。负样本是通过随机配对生成。
- 输入 x i 、 x j x_{i}、x_{j} xi、xj通过两个模型分别输入,输出两个向量。最后一层的激活函数一般是tanh,保证值域为(-1,1)。最后计算两个向量额距离。
- x i 、 x j x_{i}、x_{j} xi、xj为同一语义信息空间的数据,比如都是中文时,两个模型可以是同一个,共享参数。(比如word2vec计算文字相似度)。否则必须是两个模型(比如中文和英文、图文匹配等)它们的输出向量哎同一空间内,所以有可比性
- 度量学习只能判断是否相似,和哪一对更相似。但是不能比较哪一对更不相似。




 本文深入解读线性回归的MSE损失与正则化,以及逻辑回归的交叉熵优化。探讨AUC在评估模型性能中的关键作用,包括ROC曲线、F1分数和AUC计算。涵盖了度量学习中的对比损失概念,以及如何在不平衡数据中应用上采样和下采样策略。
本文深入解读线性回归的MSE损失与正则化,以及逻辑回归的交叉熵优化。探讨AUC在评估模型性能中的关键作用,包括ROC曲线、F1分数和AUC计算。涵盖了度量学习中的对比损失概念,以及如何在不平衡数据中应用上采样和下采样策略。

















 1085
1085

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










