【单自由度系统的谐波激励】在时域中研究单自由度系统强迫振动的某些数值方法实现研究（Matlab代码实现）

科研_研学社

于 2024-10-26 11:23:35 发布

阅读量749

点赞数 28

文章标签： matlab 算法人工智能

本文链接：https://blog.csdn.net/qq_57231208/article/details/143250795

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

【单自由度系统的谐波激励】在时域中研究单自由度系统强迫振动的某些数值方法实现研究

摘要
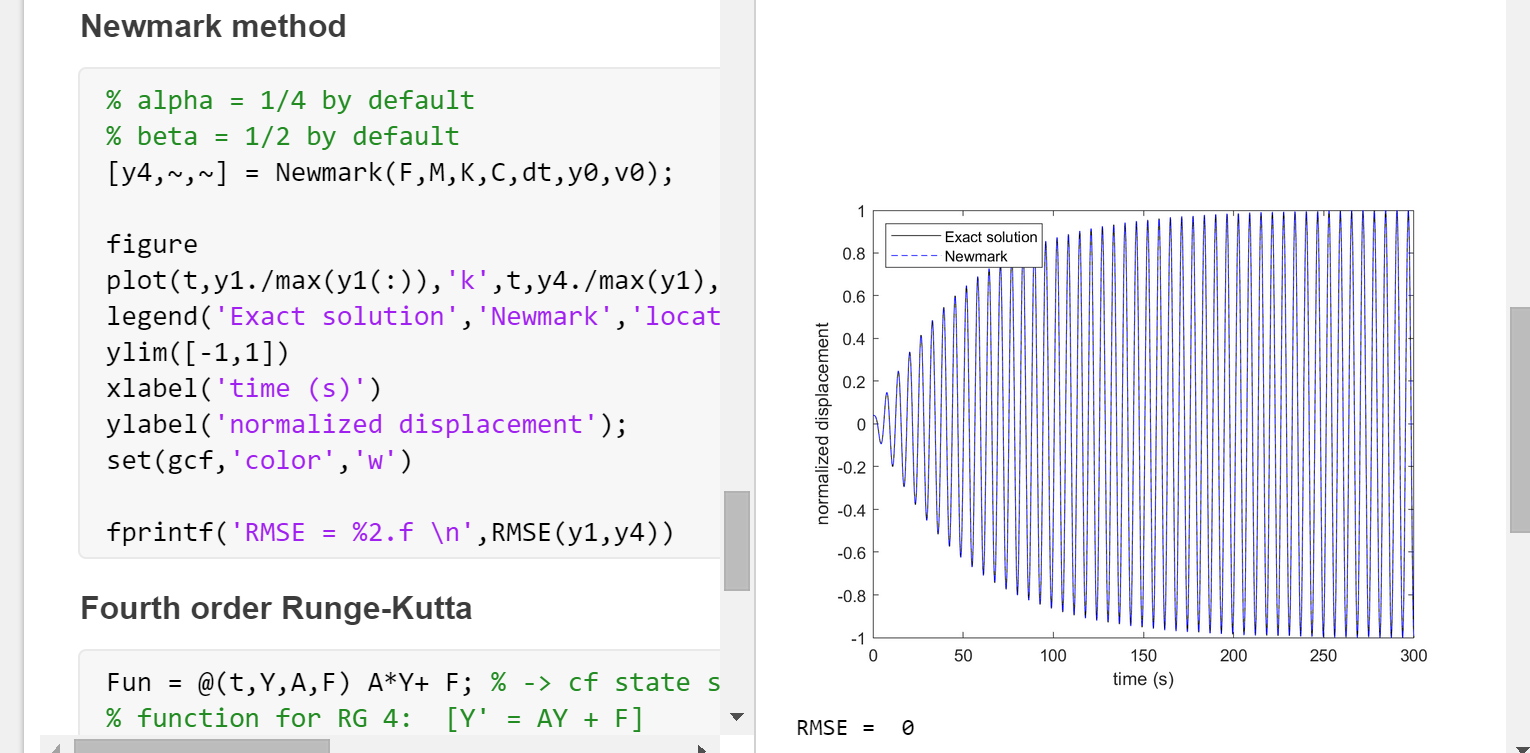
计算了谐和力激励下的阻尼单自由度（SDOF）系统的精确解。将其与Matlab内置函数ode 45、中心差分法、纽马克法和四阶龙格-库塔法提供的数值解进行比较。

函数RK4.m，使用四阶龙格-库塔法对阻尼系统的运动方程进行数值求解
函数Newmark.m，采用纽马克方法对阻尼系统的运动方程进行数值求解
CentDiff.m函数，采用中心差分法对阻尼系统的运动方程进行数值求解

📚2 运行结果

部分代码：

function [x,dx,ddx] = Newmark(F,M,K,C,dt,x0,v0,varargin)

% options: default values
p = inputParser();
p.CaseSensitive = false;
p.addOptional('alpha',1/12);
p.addOptional('beta',1/2);
p.parse(varargin{:});

% shorthen the variables name
alpha = p.Results.alpha ;
beta = p.Results.beta;

% initial acceleration
a0 = M\(F(1)-C.*v0-K.*x0);

N = numel(F);
ddx = [a0,zeros(1,N-1)];
dx = [v0,zeros(1,N-1)];
x = [x0,zeros(1,N-1)];

aDT2 = (alpha.*dt.^2);
aDT = (alpha.*dt);
A = (1./aDT2.*M+beta/aDT*C+K);

for ii=1:N-1,

B1 = F(ii+1)+M.*(1./aDT2*x(ii)+1./aDT*dx(ii)+(1/(2*alpha)-1)*ddx(ii));
B2 = C.*(beta/aDT*x(ii)+(beta/alpha-1).*dx(ii));
B3 = C.*((beta/alpha-2)*dt/2*ddx(ii));

x(ii+1) = A\(B1+B2+B3);
ddx(ii+1)= 1/aDT2.*(x(ii+1)-x(ii))-1/aDT.*dx(ii)-(1/(2*alpha)-1).*ddx(ii);
dx(ii+1)= dx(ii)+(1-beta).*dt*ddx(ii)+beta.*dt*ddx(ii+1);

end