对于机器学习的初学者来说,反向传播算法应该算是碰到的第一个难点。若是能从数学原理上解释清楚算法的做法以及为什么这么做,将使大家对算法的理解更加透彻。因此,本文将对反向传播算法进行阐释并做相对详细的数学推导,希望能帮到大家!
注:本文假定读者已熟悉前向传播过程。
一.符号说明
| 符号 | 说明 |
|---|---|
| 总层次数 | |
| 输出层单元数 | |
| 第 | |
| 第 | |
| 第 |
二.反向传播算法推导
首先明确一点,我们在训练神经网络时,需要运行梯度下降对参数进行迭代,那么我们就需要求出代价函数
对所有的参数
的导数。反向传播算法正是这样一种计算
的方法。它的本质就是计算导数。
我们先来看一下代价函数:
不妨,我们只对单次输入进行推导,输入值: 记:
其中, :输出层中第k个单元的真实值;
:输出层中第k个单元的计算值
1.求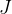 对
对 的导数。
的导数。
先求对
中每个元素的导数,由复合函数的链式求导法则
其中,
因此对
的导数为:
记:
则:
2.求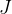 对
对 的导数
的导数
其中,
因此对
的导数为:
记
注意:此处的矩阵与前向传播中的
不同,此处不包含偏置项所对应的参数。(从
对
的形式也可以看出。)
事实上,因为前向传播过程中,第 层的激活值对
层的偏置项没有影响,亦即第
+1层偏置项并不是关于
层的激活值的函数,自然对
层的激活值求导时,并不会出现与
+1层有关的参数。
有了以上的记法,则
3.推广到 对
对 的导数
的导数
类似2中的做法,可以得到:






















 3652
3652











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








