【neural networks and deep learning学习笔记】chapter2 反向传播算法如何工作

红点雷龙XL

已于 2022-05-25 22:02:28 修改

阅读量211

点赞数 1

分类专栏：深度学习文章标签：深度学习神经网络

于 2022-05-25 20:53:04 首次发布

本文链接：https://blog.csdn.net/wentong_Xu/article/details/124972328

版权

深度学习专栏收录该内容

4 篇文章 0 订阅

订阅专栏

在上一章的内容中，学到了如何让神经网络进行梯度下降来进行学习，并最终得到我们想要的结果，那么上一章的主要得知的就是梯度下降时候的两个自由变元的选择，其中Δw,Δb选择对应的代价函数的偏导就可以实现神经网络的正向学习。

那么同样的留下了一个问题，我们如何才能让网络进行高效快速的求偏导呢？

直观方法
代价函数的两个假设
反向传播的四个基本方程
反向传播的基本流程
反向传播代码

直观方法

其中最直观朴素的方法就是从输入层至输出层一级一级的进行求偏导，最中得到结果后传递下去，这样无疑是可行的，毕竟开始设计的神经网络正向学习的目的达到了。

可以想象，这里我们选取到了第一章中举到的例子，其中输入神经元有28*28 784个神经元，通过全连接的方式输入到有15个神经元的隐藏层，也是通过全连接的方式接入输出层的10神经元。

当然这里并没有给出784个输入神经元，其中我们可以看一下有多少个权重和偏置，可以说上图中的每条线就代表存在两层相接的权重，每一个输入层后面的神经元就代表有多少个偏置b。而且这些权重和偏置需要经过至少几轮的计算（我想通过少轮的计算在正常规模的学习中很难将代价函数降到0）。那么就可以发现朴素的求解偏导是极为麻烦的一件事情，至少是较慢的一个过程。

代价函数的两个假设

代价函数的形式可以有多种，比如后续接触到的交叉熵函数等等，这里我们主要讨论一种就可以了。

对于二次代价函数来说：

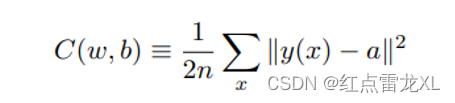
其中n是总的训练数据的量，x是输入数据，y(x)是对应的期望的输出，a (x)是当输入为x时输出层的激活函数的输出。

其中我们很明显的可以看出，当y接近a时候，也就是当网络的输出接近于期望的输出时候，C是约等于0的，当然，相差越大就离0越远，就像上一章学到的那样。

假设1

代价函数可以被写成一个在每个训练样本x上的代价函数的均值。也就是可以把整体的代价函数看成是n个代价函数做的均值。观察二次代价函数就是这样的，比如前面的1/n。

那么这样就可以对每一个训练数据都对代价函数进行求导，在训练的时候是对每一个训练数据，每一次训练就可以调整一轮权值。当前还有一个好处就是可以让代价C于训练的数据量无关，方便后续的随机梯度下降。

假设2

代价可以写成神经网络输出的函数。

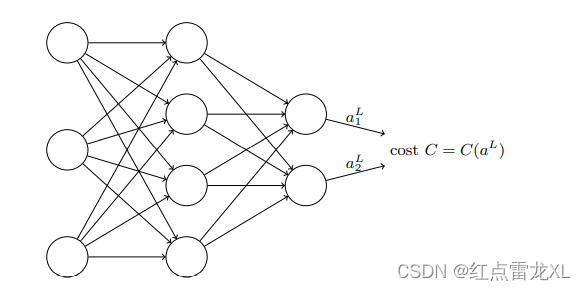
在这个假设下，我们的二次代价函数也就可以写作对于输出的激活值的函数。形式如下：

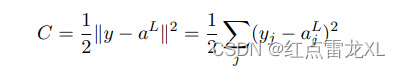
当然，在这个二次代价函数的形式中，可以看到这个函数的输出还依赖期望输出y。对于这里的理解是这样的，其中对于整个网络来说，在学习训练的过程中，我们给定输入x和期望输出y（x），就像在学习过程中我们推导的那样，我们只需要对于两个自由变元Δw,Δb进行约束让网络正向学习就行了，对于网络的实际输入x和y我们认为这是我们输入的不同数据的参数，所以就不需要认为y同样是一个变量了。

Hadamard乘积

在学习的过程中还接触到了一种乘积的形式，称为hadamard乘积，s ⊙ t 。

乘积的基本运算就是向量的对应元素相乘，如下形式

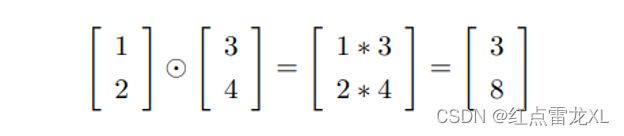
好的矩阵库通常会提供这种乘积的快速实现，在反向传播的时候用起来很方便。

反向传播的四个基本方程

反向传播其实时对权重和偏执的变化影响代价函数过程的理解，最终含义就是计算权重和偏执的代价函数C上的偏导数 $\small \frac{\partial C}{ \partial w_{jk}^l}$ 和 $\small \frac{\partial C}{ \partial b_j^l}$ 。为了计算这些偏导，引入了一个变量 $\delta_j^l$ ，称之为第 $\small l$ 层的第 $\small j$ 个神经元的误差。我们定义误差为： $\small \delta_j^l = \frac{\partial C}{\partial z_j^l}$ 。

下面就是反向传播的四个方程。

反向传播的基本流程

注意：在实践中实现随机梯度下降时候我们是需要小批量数据的循环。

反向传播代码

这里我们也可以通过书中给出的实例看到关于反向传播的具体代码。

    def backprop(self, x, y):
        """Return a tuple ``(nabla_b, nabla_w)`` representing the
        gradient for the cost function C_x.  ``nabla_b`` and
        ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
        to ``self.biases`` and ``self.weights``."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = (self.cost).delta(zs[-1], activations[-1], y)
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in range(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

上面基本上就是我第二章学习的内容，对于个人来说上述的四个方程依然是不懂其中原理的。

学完了高效计算函数偏导的方式后，其实就可以对神经网络训练了，后续第三章学习的就是如何在进行学习的过程中选择一些正确的学习方式，例如解决二次代价函数潜在的问题，过度训练浪费时间问题等等。还有选择一些超参数的方法。

本章的内容可以结合实验进行。