目录
持续更新中...
注意：标题后标星号的为选学内容
1 点火公式
简化计算过程会用到，比如3.1.1.7星形线中的例题
2 定积分的微元法（元素法）
2.1 使用条件
U是所求图形面积
2.2 使用步骤
3 定积分的几何应用
主要就是对微元法的使用
要求：跳过步骤二直接写步骤三
3.1 平面图形的面积
3.1.1 直角坐标系的情形
3.1.1.1 X型
选取x作为积分变量
3.1.1.2 Y型
选x作为积分变量时，上下边界不止一条曲线，较为复杂，此时若选取y作为积分变量好求，择选y作为积分变量
3.1.1.3 双型
既可以视为X型，也可以使用Y型
3.1.1.4 复合：分割型
可以视为两个图形分别运用X型或Y型
关键：找交点定边界
有一些分割点较为含蓄，不如上面的直观：
练习：
3.1.1.5 引入参数型
函数式复杂，计算量都非常大时，可以引入一个公共的变量，用这个变量分别表示x与y
3.1.1.6 模型：摆线
应用：引入参数型
拱数：一拱代表一个三角函数的周期，比如此题，t∈[0, 2π]代表一拱
摆线图形分析：
计算过程：
注意：定积分区间的改变！！
3.1.1.7 模型：星形线
例题：
注意：书本例题中并未给出t的取值范围
3.1.2 极坐标系的情形
3.1.2.1 基本公式
3.1.2.2 练习：双纽线
3.1.2.3 练习：心形线
3.2 立体的体积
3.2.1 旋转体的体积
单侧转时可用的技巧：绕x轴转就求以x为积分变量的图形的面积，然后添π添平方得到体积，如下图：
3.2.1.1 模型：星形线
旋转轴对面是对称的，所以只求一边的面积，再用技巧（添π添平方）
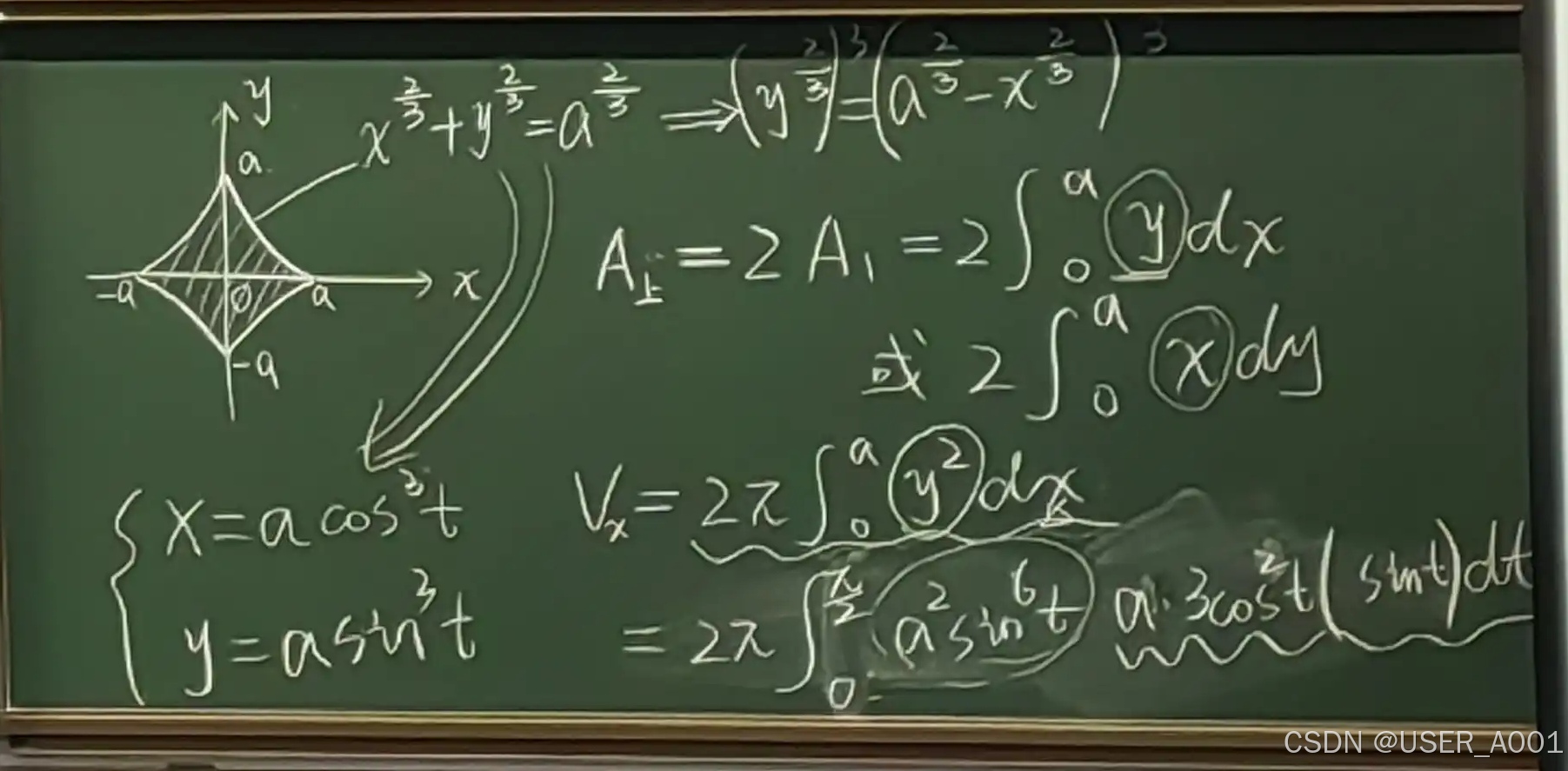
3.2.1.2 模型：摆线
1拱的面积：
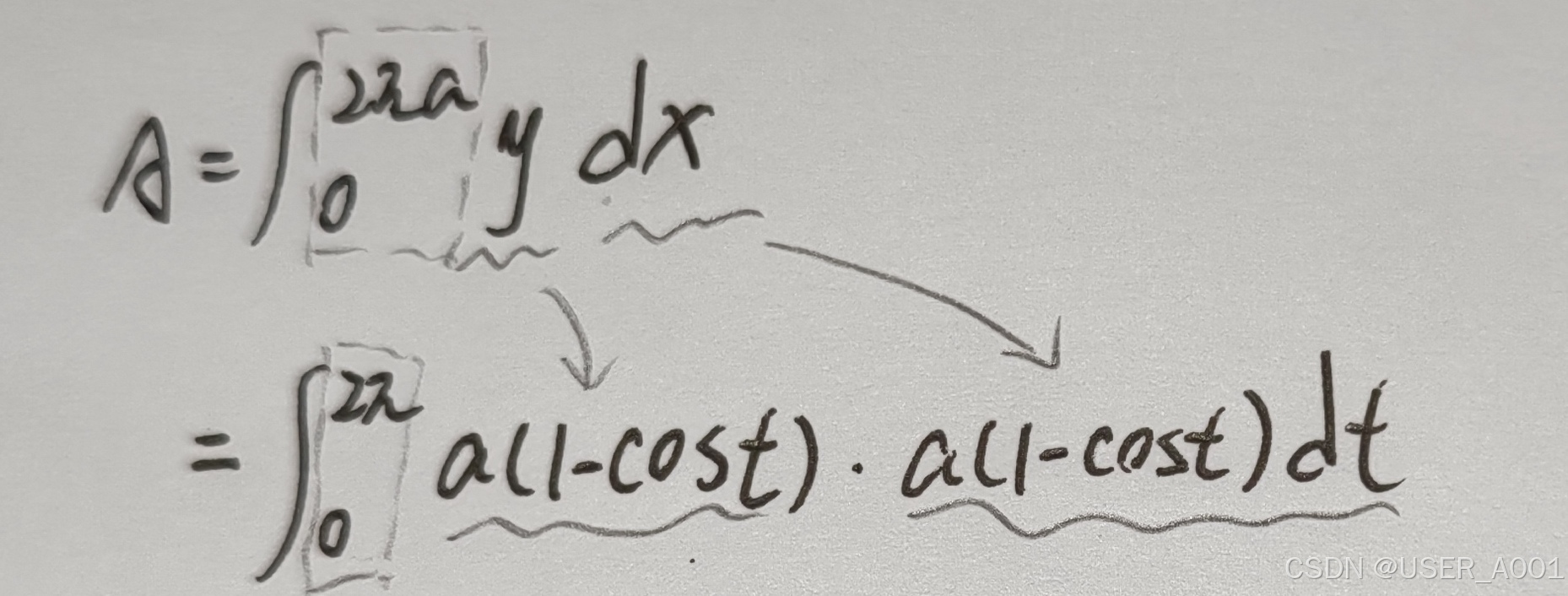
绕X轴
直接添π添平方（注意平方的位置，dt前面由dx转化来的部分不加平方）
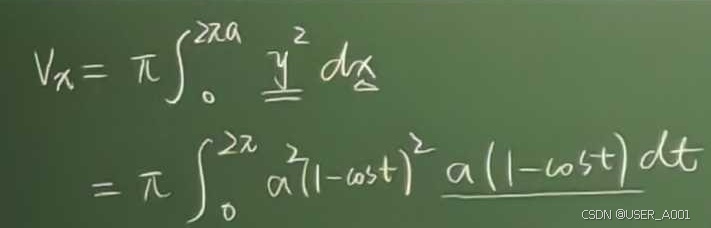
绕Y轴
方法一：普通作差
方法二：作差结论
方法原型
部分结论：
注意：dx本来就小，平方之后更小，所以忽略
* 总的结论：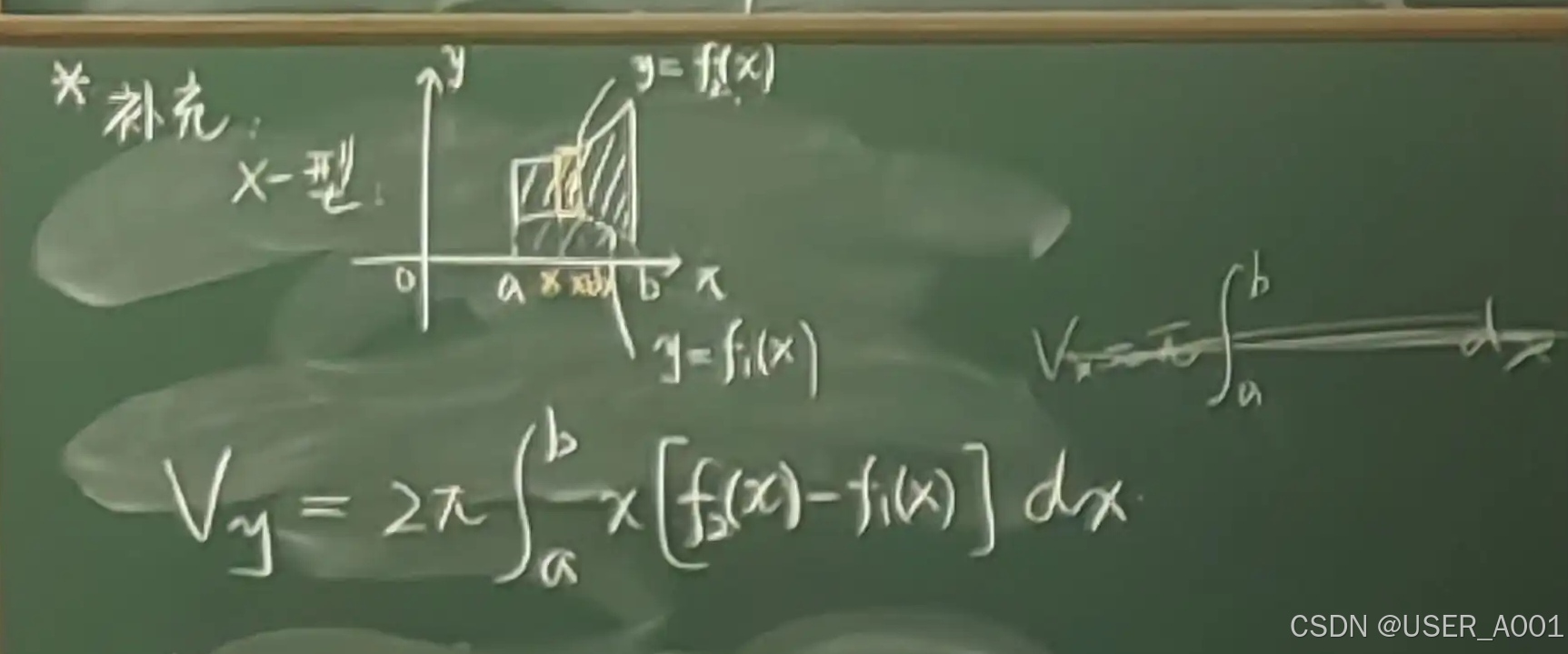 
注意：当f₁(x) = 0时，即为上方"部分结论"
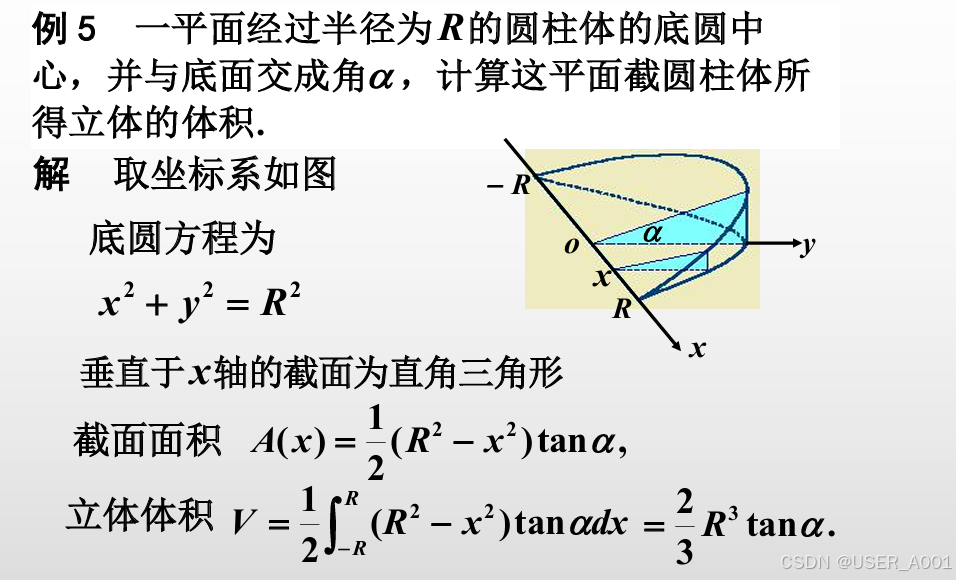
3.2.2 已知平行截面面积的立体的体积 *
例题：
3.3 平行曲线的弧长
3.3.1 基本公式
以下几种情形都基于该公式
3.3.2 直角坐标方程的情形
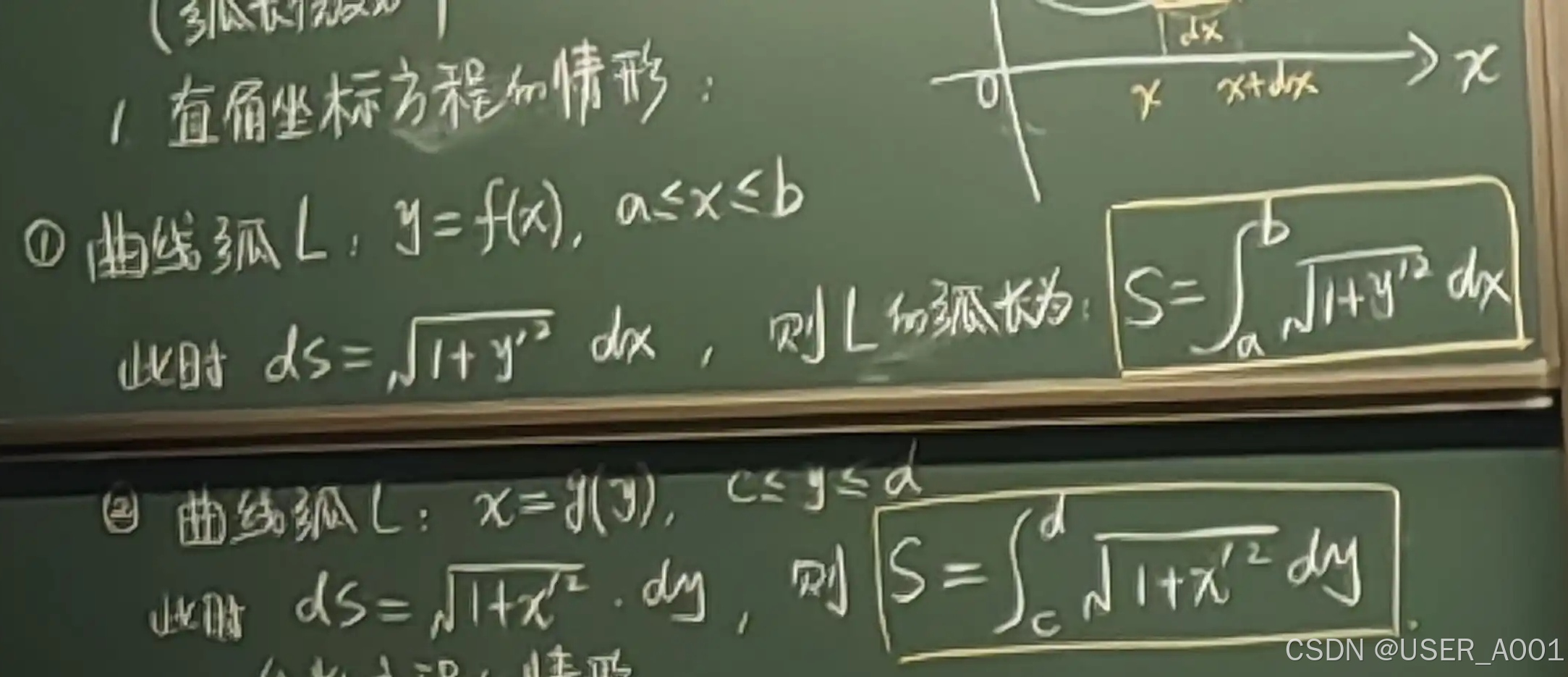
3.3.3 参数方程的情形
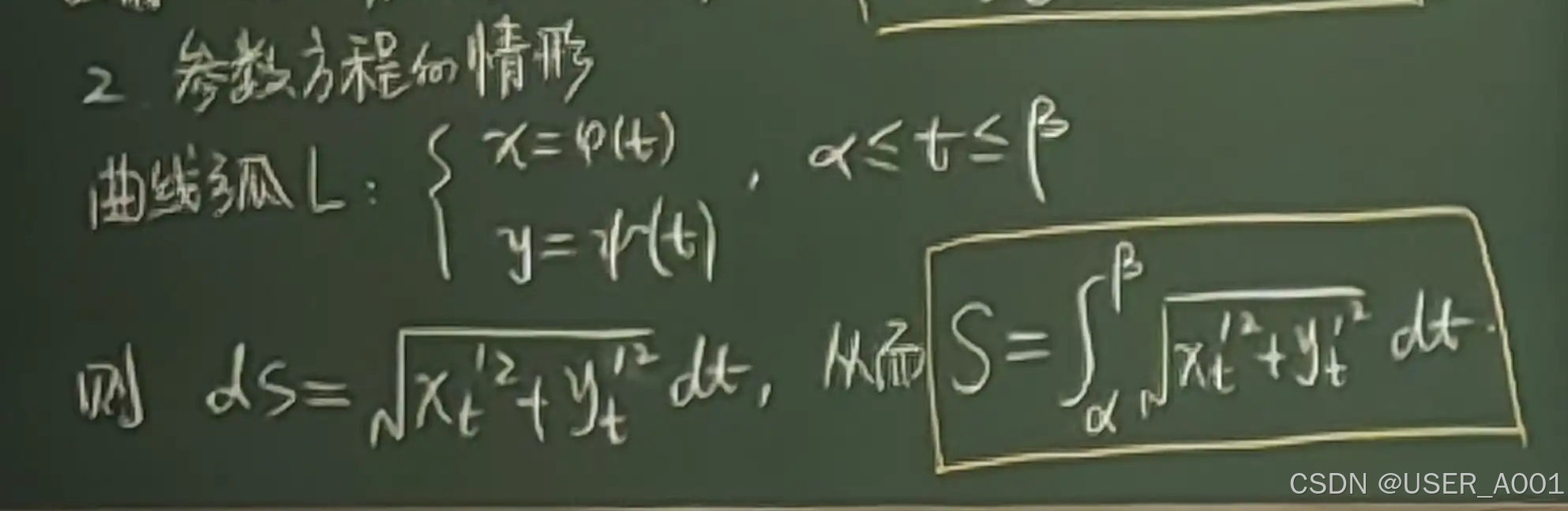
3.3.4 极坐标方程情形
推导过程：
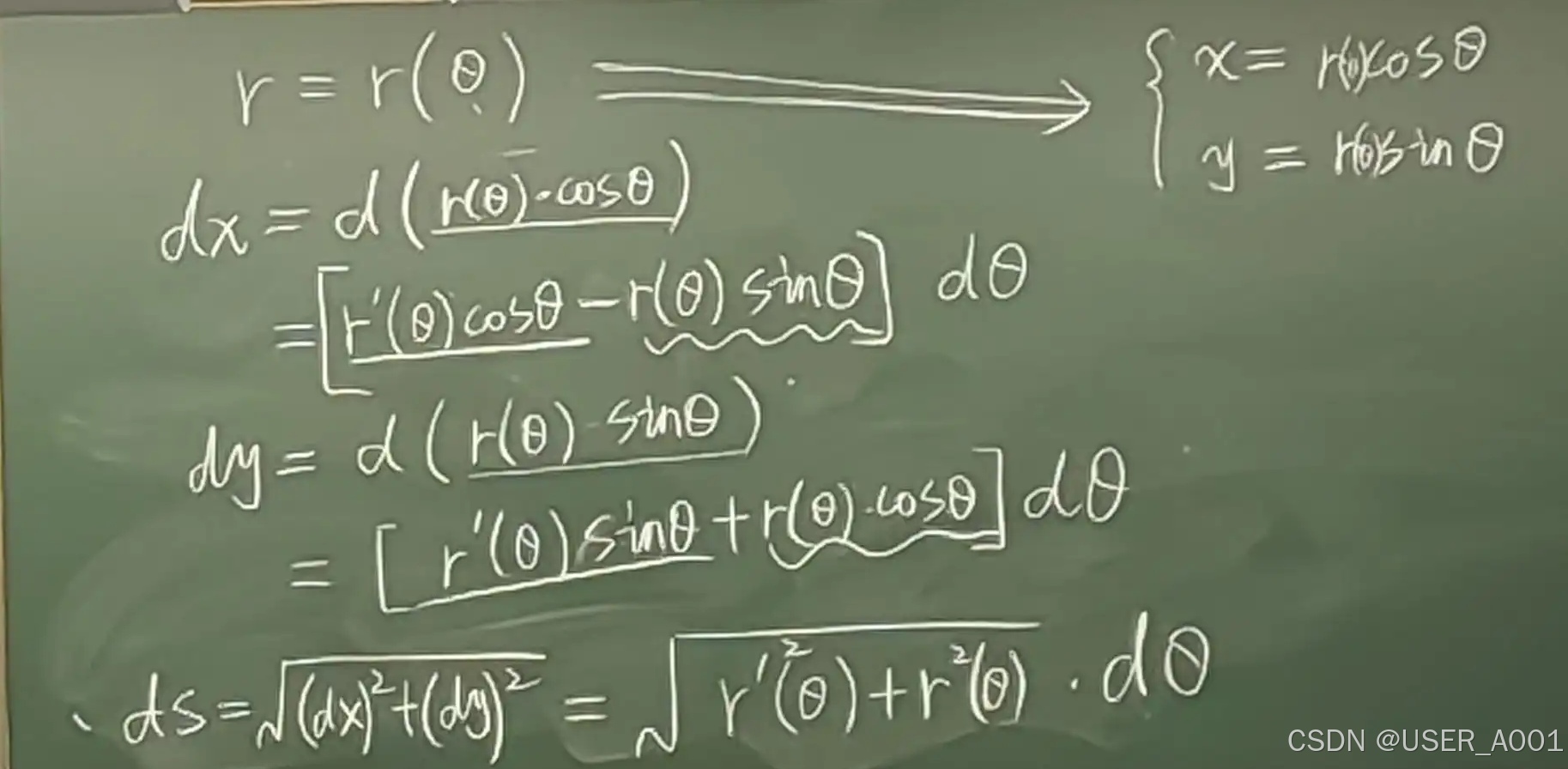
练习：星形线全长
扫一扫
449
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
