Controlling COVID-19 transmission with isolation of influential nodes

abstract

   为了了解任何传染病爆发的传播动态，识别有影响力的节点在复杂的网络中起着至关重要的作用。在大多数传染病暴发中，一些关键节点的活动可以引发疾病在人群中的快速传播。识别并立即隔离那些有影响的节点可以有效阻止疾病传播。本文提出了一种采用新颖公式的相似理想解偏好顺序（TOPSIS）方法来检测复杂社交网络中有影响力和排名靠前的节点，其中涉及对复杂社交网络的结构组织进行分析和研究。网络。在所提出的 TOPSIS 方法中，几种中心性度量已被用作复杂社交网络的多属性。设计了一个新的公式来计算流行病的传播概率，以识别隔离有影响力节点的影响。为了验证所提出方法的鲁棒性，我们对目前用于评估节点重要性的五种节点排序方法进行了全面比较。关键节点可以被认为是个人、社区、集群或特定区域。在两个真实网络中利用易感感染者恢复（SIR）流行病模型来检查节点的传播能力，结果说明了该方法的有效性。我们的研究结果发现，遵循适当的健康协议对有影响力的节点进行隔离或隔离可以在遏制 COVID-19 的传播率方面发挥关键作用。

关键词： 复杂网络 TOPSIS 方法 重要传播者识别 流行病模型 传播概率 节点排序

1. Introduction

   传播过程是一种自然现象，常见于生物、电学、社会、化学等许多领域。复杂网络已被广泛用于确定最有效的节点和基于传播能力的排名[1,2]。与其他节点相比，有影响力的节点在病毒式营销、谣言传播、疾病爆发等许多应用中的复杂网络中发挥着重要作用。然而，选择一组有影响力的节点可能需要考虑节点之间的相互影响，而不是简单地选择具有实质性影响的节点。此外，在传播过程后选择初始节点集以最大化传播规模是非常具有挑战性的。为了分析和控制信息传播过程，复杂网络需要识别有影响力的网络传播[3-5]。有影响力的传播者是在复杂网络中作为传播过程的控制器或最大化者运行的关键节点。例如，流行病学网络通过控制这些有影响力的节点行为来管理病毒传播，从而利用它们作为最大化器来扩展社交网络中的信息传播[6]。在文献中，已经提出了多种索引方法来确定有影响力的网络传播者[7-9]。现实世界由许多复杂的网络组成，包括社交网络、生物网络、研究网络和运输网络。现实世界的复杂网络是不受约束的，通常可以分为无权网络和无向网络。识别和控制此类网络中的信息传播过程对决策活动有重大贡献。它具有市场广告、谣言控制、疾病控制、创新传播等多种功能。由于影响者是信息传播以帮助决策过程的关键参与者，因此有必要识别复杂网络中的影响者[10-15]。

     近年来，复杂网络分析由于其与各种研究问题的高度相关性而得到了广泛的应用和发展。最近，已经开展了各种相关研究来研究复杂网络的重要属性以及它们如何在证据理论和不同决策场景建模中发挥作用[16-20]。叶等人。 [21]采用博弈动力学和网络结构的协同进化研究了多智能体动力学中的群体行为适应性和福利动力学适应性。对复杂网络和基于知识的系统中的有影响力的节点进行排名近年来非常流行，因为这个概念在各个领域都非常有洞察力。刘等人。 [22]提出了一种结合局部和全局信息的广义力学模型来识别复杂网络中的有影响力的节点。在这项工作中，使用了十个真实网络来验证所提出方法的有效性。为了解决几种中心性度量的局限性，Wen 等人。 [23]提出了一种基于分形属性的多局部维度（MLD）来识别复杂网络中的重要传播者。为了证明所提出方法的有效性和合理性，研究中利用了一些现实世界和理论复杂网络。复杂网络在证据理论中有许多实际应用。为了可视化个体之间的关系，Zhao和Deng[24]提出了一种基于证据相似性的证据理论复杂网络模型。在最近的工作[25]中，考虑了节点的结构相似性，并将原始转移矩阵替换为相似性矩阵，以考虑节点与其邻居之间的转移概率不相同的事实。 Yu 等人基于节点排序方法。 [26]引入了一种新颖的重新排序算法，通过信息传播函数来确定复杂网络的一组有影响力的节点。杨等人。 [27]研究了如何基于节点局部中心性和网络嵌入来识别复杂网络中有影响力的传播者。人们从不同的角度提出了几种方法来识别复杂网络中的关键节点。其中，引力模型可以根据局部和路径信息有效地找到重要节点。对此，李等人。 [28]使用广义引力模型来识别复杂网络中有影响力的传播者。纳姆蒂尔萨等人。 [6]提供了基于网络全局结构特性识别有影响力的传播者的最佳方法。 Gupta 和 Mishra [29] 研究了复杂网络中的信息传播，并使用网络结构识别了一组前 N 个有影响力的节点。

   在流行病学网络中，可以通过分析有影响力的节点的行为来控制病毒传播。从任何拓扑位置，都可以通过计算每个节点的传播能力来控制传播过程。随着多个 COVID-19 大规模疫苗接种计划在不同国家展开，COVID-19 的几种强毒变种已开始对新病例激增构成威胁。从COVID-19大流行开始，许多数学建模方法在设计有弹性的公共卫生政策以控制疾病传播方面做出了很大贡献[30-33,42]。然而，有效识别有影响力的传播者仍然是一个有待解决的难题。本文提出了一种新颖的公式相似理想解偏好顺序（TOPSIS）方法，可以有效地识别复杂社交网络中有影响力的传播者，其中涉及对网络结构组织的分析和研究。尽管文献中提供了许多节点排序方法，但实验结果表明，我们提出的方法在各种网络连接结构上优于所有当代方法。我们提出的方法与计算成本较高的更复杂的方法具有竞争力。我们的实验结果发现，我们提出的方法可以从复杂的网络中有效地识别出最具影响力的传播者。由于实际疾病传播率因网络而异，感染概率是了解真实疾病传播情况的一个富有洞察力的参数。尽管很难估计网络的真实感染率，但我们计算了与网络流行阈值相关的疾病传播概率。两个真实的 COVID-19 网络已用于验证所提出的方法在识别和排名有影响力的节点方面的稳健性。最后，与当代方法进行全面比较，以说明所提出方法的有效性。

2. Materials and methods

   对有影响力的个人或组织进行有效且有影响力的识别有助于控制 COVID-19 的传播。在本节中，提出了几种方法来识别随机网络中的重要节点。识别社交或复杂网络中有影响力的传播者是一项重大挑战。为了解决这个问题，本文提出了几种中心性度量，例如特征向量中心性（EC）、度中心性（DC）、介数中心性（BC）和接近中心性（CC）。接下来，提出了 TOPSIS 以及新的修改权重来识别重要且有影响力的节点。

2.1. Node ranking using centrality measure

  在本节中，提出了诸如DC[14]、CC[15]、BC[16]和EC[12]等中心性度量来识别复杂或社交网络内有影响力和重要的节点。从中心节点到所有其他节点的最短距离的倒数和表示接近中心性。因此，紧密中心性得分越高，该节点与其他节点越接近。介数衡量通过节点的最短路径的数量。特征向量中心性是另一种检测重要且有影响力的节点的方法，由 Bonacich 首先提出[17]。在特征向量中心性方法中，节点的重要性和影响力基于邻居的数量及其质量。 DC、CC、BC 和 EC 方法定义如下：

A。度中心性

  节点 i 的度中心性 (DC) 表示为 CD(i)，定义为：

  其中，N为节点总数，i为焦点节点，j代表所有其他节点，xij代表节点i与节点j之间的连接。如果nodei与节点j连接，则xij值为1，否则，它是0。通过最小化中介节点的数量，在二元网络中找到最短路径，并且直接或间接嫁接两个节点的最小连接数定义其长度[14]。二元最短距离定义如下[18],】

  这里，节点 i 和 j 之间的路径上的中介节点的数量由 h 定义。

b.紧密中心性法

  Nodei 的紧密中心性 CC(i) 定义如下：

其中，dij是节点i和节点j之间的距离。

C。介数中心性法

节点 i 的介数中心性 CB(i) 定义为：

参数 pkl、pkl(i) 和 NN−1 ðÞ 2 的定义如下： pkl：节点 k 和节点 l 之间的二进制最短路径数，pkl(i)：经过节点 i 的路径数。 NN−1 ðÞ 2 ：用于标准化介数中心性值。

d.特征向量中心性法

  如果 A 是一个 n × n 相似度矩阵，则节点 i 的特征向量中心性 xi 定义如下：

其中，xi 是属于矩阵 A 最大特征值的归一化特征向量中的第 i 个条目，aij 是相似矩阵 A 的数组，λ 是最大特征值，n 是顶点数。

2.2. Weighted TOPSIS method

  TOPSIS方法[19]是由Hwang和Yoon于1981年开发的[20]。它是社会或复杂网络中的一种排序概念和应用方法。标准TOPSIS方法用于选择同时距负理想解最远和距正理想解最短的解。收益准则最大化和成本准则最小化是正理想解，而收益准则最小化和成本准则最大化是负理想解。

定义 1.2。假设 D = (xmn) 是一个决策矩阵，由标准和替代方案组成。决策矩阵 R = (rij) 可以归一化如下，

加权决策矩阵 A =(vmn) 可以通过将归一化决策矩阵各列中的相关权重相乘得出，如下所示：

其中 wj 是 j 标准的权重。本文提出新的权重如下：

正理想解和负理想解定义如下：

其中，Kb和Kc分别是收益准则集和成本准则集。根据解 A+ 和 A−，我们有，

  解 Si+ 和 Si− 是基于欧几里德距离的分离度量。使用正理想解 Si+ 和负理想解 Si−，相对接近度可以计算为：

所有节点都根据与理想解决方案的相对接近程度进行排名。这意味着有影响力且优先级较高的节点具有较高的 Ci。

2.3. Analysis of time complexity

  时间复杂度涉及计算加权决策矩阵。此步骤的复杂性基于每次迭代。需要与向量进行一次矩阵乘法，其中时间复杂度为 O (n2)，其中 n 是向量的长度。然而，如果稀疏矩阵每行平均有 m 个非零元素，则矩阵与向量的乘法可以在 O(mn) 时间内完成。

2.4. Testing of the proposed method

  在本节中，如图所示的四个图网络。 1-4，来自以前发表的论文[1,34-36]，用于说明中心性度量的应用以及基于与理想解决方案的相对接近度提出的方法。参考文献 [34] 提出了第一个包含 12 个节点和 13 个边的网络。图 1 显示了所提出的网络，其中四个排名靠前的节点以红色突出显示。

  根据图 1 所示的第一张图的连接和未连接节点，该图的邻接矩阵如下：

图 1. 包含 12 个节点和 13 个边的网络 [34]。四个排名靠前的节点以红色突出显示。

因此，图1的决策矩阵D=(xij)可如下获得。

采用表1所示的DC、BC和EC的三个中心性度量来推导决策矩阵。等式。利用式(6)对决策矩阵进行归一化，则归一化后的决策矩阵R=(rij)可推导如下：

这里，T是矩阵R的转置，利用式(8)得到加权决策矩阵A =(vmn)as，

   等式中显示的新权重。利用式（8）求得加权决策矩阵。正理想解 A+ 和负理想解 A− 是使用等式导出的。 （9）和（10），

分离测量 Si+ 和 Si− 使用等式计算。 (11) 和 (12) 分别如下，

  表 2 列出了基于与图 1（图 1）理想解的相对接近程度的节点排名结果。

表 2 根据与图 1 所示图表的理想解决方案的相对接近程度进行节点排名 [34]。

在式(13)中，Ci的值是使用Si−和Si+的值计算的。 Ci 的最大值属于网络中排名最高的节点。如表 2 所示，C9 1⁄4 min i1⁄41, ...,12 Ci fg1⁄40:1732 和 C7 1⁄4 max i1⁄41, ...,12 Ci fg1⁄40:8034 。因此，在图 1 的 12 个排名节点中，节点 8 排名第一，节点 9 排名最后。

  

图 2. 包含 13 个节点和 19 个边的网络 [35]。四个排名靠前的节点以红色突出显示。

图 3. 一个示例网络由 23 个节点和 40 个边组成 [1]。虽然节点23的度数低于节点1，但其影响力可能更高。四个排名靠前的节点以红色突出显示。

图 4. 一个示例网络由 24 个节点和 29 个边组成 [36]。虽然节点23的度数低于节点1，但其影响力可能更高。四个排名靠前的节点以红色突出显示。

基于与图 2-4（图 2-4）理想解决方案的相对接近程度的节点排名如表 3-5 所示。

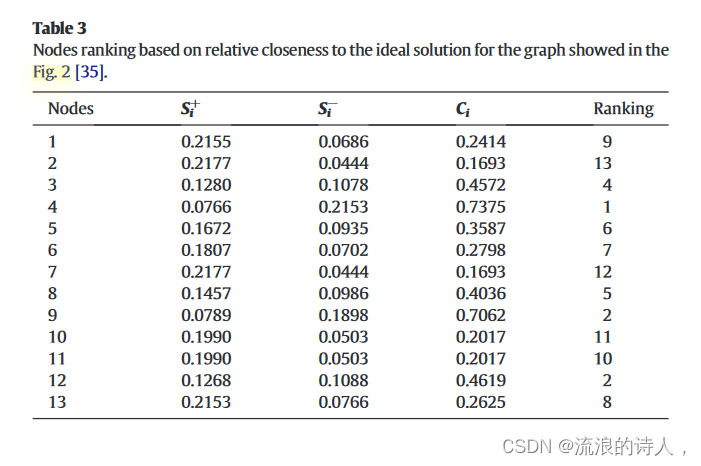
表 3 根据与图 2 所示图表的理想解决方案的相对接近程度进行节点排名 [35]。

表 4 根据与图 3 所示图表的理想解决方案的相对接近程度对节点进行排名 [1]。

表 5 根据与图 4 所示图表的理想解决方案的相对接近程度进行节点排名 [36]。

根据表 3，C2 1⁄4 min i1⁄41, ...,13 Ci fg1⁄4 0:1693 和 C4 1⁄4 max i1⁄41, ...,14 Ci fg1⁄4 0:7375，则，在图 2 的 13 个排名节点中，节点 4 排名第一，节点 2 排名最后。如表 4 所示，C5 1⁄4 min i1⁄41, ...,23 Ci fg1⁄4 0： 1593 和 C1 1⁄4 max i1⁄41, ...,23 Ci fg1⁄4 0:8836，因此在图 3 的 23 个排名节点中，节点 1 排名第一，节点 5 排名最后。表 5 显示，C22 1⁄4 最小 i1⁄41，...,24 Ci fg1⁄4 0:0865 和 C1 1⁄4 最大 i1⁄41，...,24 Ci fg1⁄4 0:7479。因此，在图 4 的 24 个排名节点中，节点 1 排名第一，节点 22 排名最后。

2.5. A new formula for disease spread probability in a complex network

  在本节中，我们研究了隔离受感染影响节点的复杂网络中的疾病传播概率。假设 G 为建议图，N 为总节点数，E 为节点数排名靠前的有影响力的节点，图Gj的流行病传播概率P(Gj)可以定义如下：

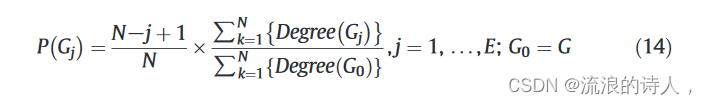
为了说明疾病传播概率在复杂网络中的应用，我们计算删除 2 个排名第一的节点后的传播概率，如下所示：

因此，在包含 12 个节点和 13 个边的复杂网络（见图 1）中，删除前 2 个排名靠前的节点后，流行病传播概率将降低 P(G0) − P(G2)=1− 0.7404 = 0.2596 。

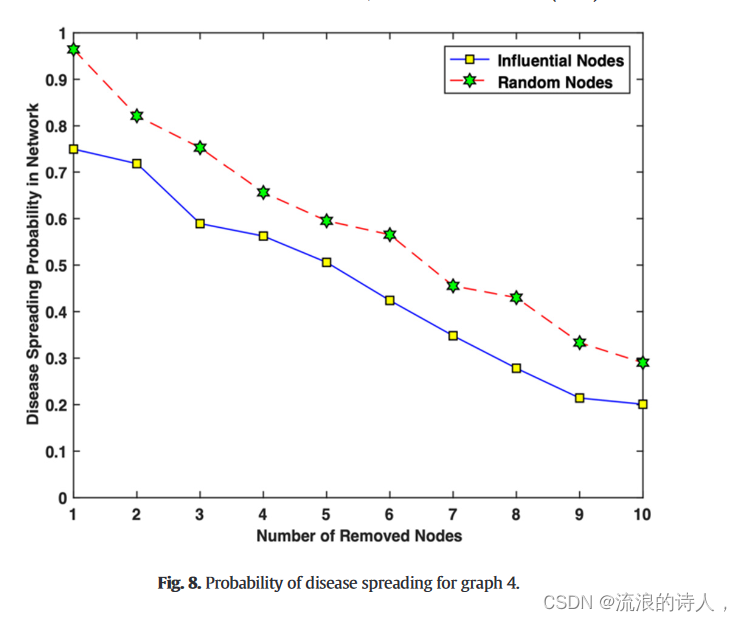
  图5-8示出了图1-4中所示的流行病传播概率的降低。 1-4，通过逐步删除九个受感染的顶级节点。可以看出，通过去除排名靠前的前几个有影响力的节点，流行病传播的概率下降得更快。对于所提出的图网络，假设疾病传播概率等于 1，而无需删除任何节点。结果显示了有效节点在复杂网络中传播流行病的力量。

因此，有影响力的节点隔离可以非常有效地控制包括COVID-19在内的流行性疾病的传播。

2.6. Node ranking performance evaluation with SIR model

  SIR（易感-感染-恢复）模型[37,38]已应用于节点排名性能的评估[39]。排名靠前的节点的传播能力可以使用SIR模型来评估。图9显示了高危人群中流行病传播的SIR模型。

  SIR模型的动态系统可以用数学表示如下：

其中，γ 是感染者中康复者的比率，λ 是感染率，取决于每个伴侣的传播概率（β > 0）、单位时间每个人的伴侣数量（r > 0）以及感染者与性活跃者的比例 IþSþR 如下，

在所提出的模型中，S类中的易感群体或健康节点将以传播率λ被感染。利用初始条件S(0)=S0、I(0)=I0和R(0)=R0系统(15)的解析解如下：

在SIR模型中，S(t)表示易感节点或健康个体的数量，I(t)表示能够将疾病传播给健康个体或易感个体的感染节点或感染个体的数量，R(t) ）是从感染者中康复的人。一个随机易感邻居被每个受感染节点感染，每一步的概率为 λ。在本文中，出于均匀性目的，感染率假设为 λ 1⁄4 λ 1⁄4 0:3，恢复率假设为 γ = 0.05。传播率可以指定节点在网络上疫情传播的影响范围。疾病不仅可以通过受感染的节点传播到其直接邻居，还可以通过中介传播到其高阶邻居。因此，影响节点的检测对于网络流行病的传播具有重要作用。

3. Results and discussion

  本节研究参考文献 [85, 86] 中关于大流行病 COVID-19 的两个网络图。

图10显示了所提出方法的流程图。第一张图显示了葡萄牙的六个地区及其一些联系 [40]。

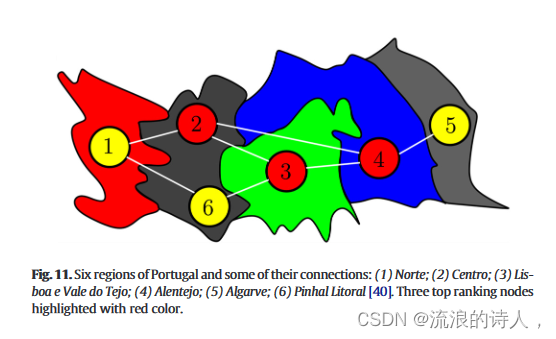
图 11. 葡萄牙的六个地区及其一些联系： (1) 北部； (2) 中心； (3) 里斯本和特茹谷； （4）阿连特茹； (5) 阿尔加维； (6)皮哈尔滨海[40]。三个排名靠前的节点以红色突出显示。

该图的三个排名最高的节点以红色突出显示（图 11）。第二张图显示了希腊 COVID-19 感染的可见性 [41]。

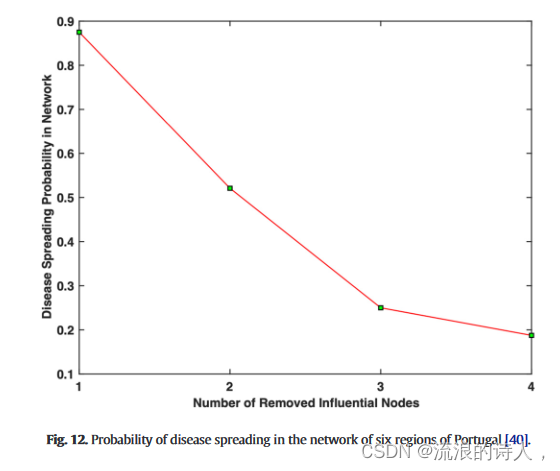
图 12. 葡萄牙六个地区网络中疾病传播的概率 [40]。

排名最高的 9 个节点以红色突出显示（图 12）。根据图 11，Centro、Lisboa e Vale do Tejo 和 Alentejo 地区具有影响力地区。隔离这些地区将减少大流行性 COVID-19 的爆发，并且大流行性疾病传播的可能性会更快地降低。

  在本文中，许多中心性度量及其应用被用于检测有影响力的节点。所有这些方法都有一些限制和缺点，并且都只关注一种中心性度量。信息流对于识别网络中有影响力的节点至关重要。正如几位作者指出的，有必要在具有不同信息的不同网络中采用不同类型的中心性度量[12,14-16]。

3.1. Analysis of Portugal regions

   图11显示了葡萄牙六个地区的图表：（1）北部； (2) 中心； (3) 里斯本和特茹谷； （4）阿连特茹； (5) 阿尔加维； (6)皮哈尔滨海[40]。该图由 6 个节点和 7 个边组成，三个排名靠前的节点以红色突出显示。

表 6 突出显示了按 DC 衡量标准、CC 衡量标准、BC 衡量标准、EC 衡量标准排名靠前的节点，葡萄牙六个地区网络的基本 TOPSIS 方法和建议方法。表 3 显示我们对所提出的方法、基本 TOPSIS 方法和 BC 测量方法得到了相同的结果。葡萄牙6个地区的疾病传播概率如图11所示。如图 12 所示，如果删除三个有效节点，则 COVID-19 传播的概率下降得更快（从 P(G0)=1 下降到 P(G3)= 0.2562）。

  

图 13. 葡萄牙六地区网络节点 4 和节点 2 之间的累计感染数量与时间的关系。

图 13 显示了葡萄牙六个地区网络中节点 4 和节点 2 之间的累计感染数量与时间的关系。从图 13 可以看出，节点 4 感染整个网络节点的速度更快，因此节点 4 的排名高于节点 2。因此，该方法比 DC 方法效果更好。

图 14. 葡萄牙六地区网络节点 4 和节点 5 之间的累计感染数量与时间的关系。

上述网络的节点4和节点5之间的累计感染病例数与时间的关系如图14所示。根据分析，节点4在感染所有网络节点方面表现优于节点5。因此，所提出的方法比 CC 和 EC 方法效果更好。表 6 总结了使用 DC 测量、CC 测量、BC 测量、EC 测量、基本 TOPSIS 方法和针对六个葡萄牙地区网络提出的方法的运行时间顺序为 RTDC < RTEC < RTBC < RTCC < RTTOPSIS 方法 < RTPROPOSED 方法（RT：运行时间） 。

3.2. Analysis of Greece

    图 15. 希腊的 COVID-19 感染可见度 [41]。九个排名靠前的节点以红色突出显示。

图 15 显示了希腊 COVID-19 传播的网络概况 [41]。该网络图由 43 个节点和 107 个边组成，其中 9 个排名靠前的节点以红色突出显示。如图 15 所示，所提出的网络图被分为五个簇，即 Q1 到 Q5。在前九个节点中，排名分别为 5、8、3 和 1 的 9、11、17 和 19 四个节点位于第一集群 Q1 中。 9 个有效节点均不位于第二集群 Q2 中。排名为 5 和 7 的有影响力的节点 26 和 32 分别是分别位于第三和第四集群Q3和Q4，而排名分别为4、2和9的三个节点35、37和42属于第五集群Q5。

  

表 7 总结了按 DC 测量、BC 测量、EC 测量、基本 TOPSIS 方法和希腊 COVID-19 感染可见性网络提出的方法排名前九的节点[41]。使用 DC 测量、CC 测量、BC 测量、EC 测量、基本 TOPSIS 方法和针对九个希腊 COVID-19 传输网络提出的方法的运行时间顺序为 RTBC < RTEC < RTDC < RTCC< RTTOPSIS 方法 < RT 建议方法（RT：运行时间）。去除 9 个影响节点后的希腊 COVID-19 感染可见性网络的疾病传播概率如图 16 所示。

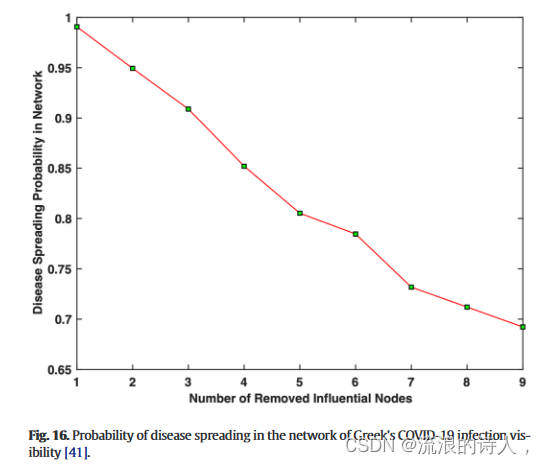
图 16. 希腊 COVID-19 感染可见度网络中疾病传播的概率 [41]。

从图 16 中可以看出，COVID-19 的传播概率下降得更快（从 P 下降）。 (G0)=1toP(G3)=0.8137)，因为五个有效节点被删除。

  

图 17. Greek [41] 网络中节点 19 和节点 37 之间的累计感染数量与时间的关系。

图 17 显示了 Greek 网络中节点 19 和节点 37 之间的累计受感染数量与时间的关系图。它强调了节点 19 比节点 37 更快地感染网络中所有健康节点的事实，因此节点 19 的排名高于节点 37。希腊Covid-19感染网络的节点9和节点32之间的累计感染数量与时间的关系如图18所示。

图 18. Greek [41] 网络中节点 9 和节点 32 之间的累计感染数量与时间的关系。

从结果中我们发现，节点9比节点32更快地感染网络中的所有健康节点，因此节点9的排名高于节点37。

  

图 19. Greek [41] 网络中节点 42 和节点 23 之间的累计感染数量与时间的关系。

图 19 显示了 Greek 网络中节点 42 和节点 23 之间的累计感染数量与时间的关系图。可以看出，节点 42 感染所有网络健康节点的速度比节点 23 快得多，因此节点 42 的排名高于节点 23。希腊网络的节点 37 和节点 17 之间的受感染累积数量与时间的关系如图 20 所示。

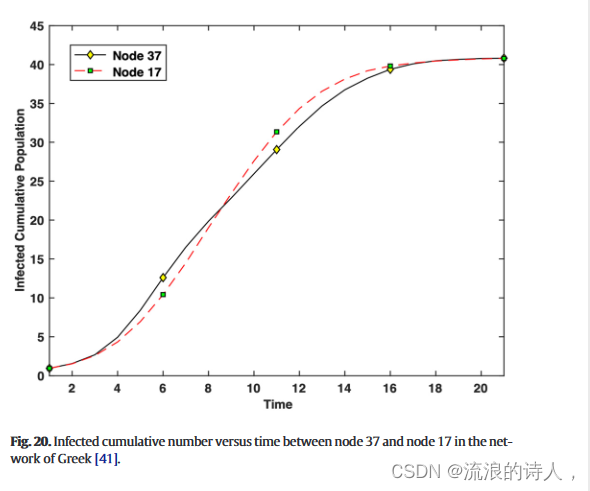
图 20. Greek [41] 网络中节点 37 和节点 17 之间的累计感染数量与时间的关系。

结果图描绘了节点 37 和节点 17 可以以几乎相同的速度和功率感染网络中的所有健康节点。可以看出，在时间1到9之间，节点17比节点37工作得更好，但在时间9到21之间，相反的现象很明显。

图 21. Greek [41] 网络中节点 19 和节点 43 之间的累计感染数量与时间的关系。

图 21 显示了希腊网络节点 19 和节点 43 之间的累积病例数与时间的关系。同样明显的是，节点 19 感染所有网络健康节点的速度比节点 43 快得多

4. Conclusion

   为了在复杂的社交网络中高精度地检测有影响力的节点，提出了一种改进的TOPSIS方法以获得更有效的权重。这项研究展示了如何更有效地检测复杂网络中的有影响力的节点，以控制 COVID-19 在人群中的传播。还使用新提出的公式计算了有影响力节点的传播概率，该公式也说明了关键节点的排名重要性。实验结果表明，移除有影响的节点可以降低 COVID-19 的传播概率。因此，检测 COVID-19 复杂网络中的有影响力的节点对于减缓疾病传播速度可能非常有洞察力。 SIR流行病模型在两个真实的COVID-19传播网络中使用，以验证所提方法的效率。结果表明，与传统方法相比，该方法能够更成功地找到有效节点，且精度更高。