CVPR2024 | EGS-TSSA | 通过精确组稀疏训练实现可迁移结构稀疏对抗攻击

---

论文链接

本文 “Transferable Structural Sparse Adversarial Attack Via Exact Group Sparsity Training” 提出了一种通过精确组稀疏训练生成可迁移结构稀疏对抗扰动的方法，在提升对抗攻击迁移性的同时，使扰动更不易察觉，在多种攻击任务中展现出优异性能。

---

摘要-Abstract

Deep neural networks (DNNs) are vulnerable to highly transferable adversarial attacks. Especially, many studies have shown that sparse attacks pose a significant threat to DNNs on account of their exceptional imperceptibility. Current sparse attack methods mostly limit only the magnitude and number of perturbations while generally overlooking the location of the perturbations, resulting in decreased performances on attack transferability. A subset of studies indicates that perturbations existing in the significant regions with rich classification-relevant features are more effective. Leveraging this insight, we introduce the structural sparsity constraint in the framework of generative models to limit the perturbation positions. To ensure that the perturbations are generated towards classification-relevant regions, we propose an exact group sparsity training method to learn pixellevel and group-level sparsity. For purpose of improving the effectiveness of sparse training, we further put forward masked quantization network and multi-stage optimization algorithm in the training process. Utilizing CNNs as surrogate models, extensive experiments demonstrate that our method has higher transferability in image classification attack compared to state-of-the-art methods at approximately same sparsity levels. In cross-model ViT, object detection, and semantic segmentation attack tasks, we also achieve a better attack success rate.

深度神经网络（DNNs）易受具有高度迁移性的对抗攻击。尤其许多研究表明，稀疏攻击因其极强的不可感知性，对深度神经网络构成重大威胁。当前的稀疏攻击方法大多仅限制扰动的幅度和数量，却普遍忽视扰动的位置，这导致攻击迁移性的性能下降。部分研究指出，存在于具有丰富分类相关特征的重要区域的扰动更为有效。基于这一见解，我们在生成模型的框架中引入结构稀疏性约束，以限制扰动的位置。为确保扰动朝着与分类相关的区域生成，我们提出一种精确组稀疏训练方法，用于学习像素级和组级的稀疏性。为提高稀疏训练的有效性，我们在训练过程中进一步提出掩码量化网络和多阶段优化算法。以卷积神经网络（CNNs）作为代理模型，大量实验表明，在近似相同的稀疏度水平下，我们的方法在图像分类攻击中比最先进的方法具有更高的转移性。在跨模型的视觉Transformer（ViT）、目标检测和语义分割攻击任务中，我们也取得了更高的攻击成功率。

---

引言-Introduction

该部分主要阐述研究背景与动机，指出深度神经网络（DNNs）存在安全隐患，易受对抗攻击，尤其稀疏攻击威胁大，当前稀疏攻击方法有缺陷，进而提出改进方法并说明其优势，具体内容如下：

1. DNNs的安全隐患：DNNs 在计算机视觉任务中表现出色，但在自动驾驶、人脸识别等对安全要求高的系统里，其分类错误会造成严重后果。引入精心设计的不可察觉扰动形成对抗样本（AEs），能轻易使这些系统产生预测错误。AEs 的迁移性使其不仅能欺骗代理模型（白盒攻击），还能影响攻击过程中未遇到的目标模型（黑盒攻击），暴露出 DNNs 的脆弱性。
2. 现有攻击方法的局限：当前多数对抗攻击方法采用 ${\ell }_p$ 范数范式约束扰动生成，如 ${\ell }_{\infty }$ 或 ${\ell }_2$ 约束会产生密集扰动；稀疏对抗攻击虽针对有限像素且成功率高，但许多稀疏攻击技术迁移性低。像可迁移稀疏对抗攻击（TSAA）虽用生成器提升了稀疏攻击的迁移性，却忽略了对扰动位置的结构约束，不同代理模型生成的扰动模式差异大，降低了迁移性，且像素级稀疏约束无法让模型学习结构语义信息。
   
   图1. 不同方法的稀疏扰动分布情况。本图突出展示了我们方法所产生的结构稀疏扰动。与可转移稀疏对抗攻击（TSAA）中呈现的分散分布不同，我们的精确组稀疏可转移结构稀疏攻击（EGS - TSSA）方法有效地将不同威胁模型生成的稀疏扰动集中到了与分类相关的区域。
3. 本文的改进方法及优势：为解决上述问题，本文构建结构稀疏性约束，使模型学习语义信息，生成更具结构化的扰动并统一扰动模式。受研究启发，让扰动尽可能存在于不同模型分类特征重要的重叠区域，以提升稀疏扰动的迁移性。通过定义组特征重要性，引入掩码量化模块，并提出多阶段优化算法进行稀疏训练。还引入新的分析方法验证有效性。文章贡献包括提出精确组稀疏训练方法、构建掩码量化网络、通过实验证明方法在迁移性方面的优势 。

---

相关工作-Related Work

该部分主要介绍了与本文研究相关的四类对抗攻击方法，分析了它们的原理和局限性，为本文方法的提出做了铺垫，具体内容如下：

1. 幅度约束的对抗攻击：这类攻击通过 ${\ell }_{\infty }$ 或 ${\ell }_2$ 范数限制扰动幅度以满足攻击要求。如 Szegedy 等人用 L - BFGS 方法开创该领域，但存在扩展性差、运行慢的问题。FGSM 通过计算梯度符号构建更快的攻击，I - FGSM 和 MI - FGSM 利用迭代和动量进一步增强攻击性能，PGD 攻击能力更强但收敛问题未完全解决。此外，还有通过改进通用对抗扰动（UAP）来提高攻击效率的方法，如Zhang等人训练具有主导特征的数据相关 UAP，GD - UAP 通过最大化卷积激活生成数据无关的 UAP，Cosine - UAP 和 TRM - UAP 分别利用余弦相似性和截断比率最大化来提升转移性。
2. 稀疏约束的对抗攻击：利用 ${\ell }_0$ 或 ${\ell }_1$ 范数限制扰动数量，使生成的扰动足够稀疏。JSMA 利用显著性度量识别对稀疏扰动最有影响的像素，PGD${}_0$通过投影到 ${\ell }_0$ 球上生成稀疏扰动，SparseFool 将 DeepFool 方法扩展到非目标性稀疏攻击，StrAttack 通过交替方向乘子法（ADMM）优化扰动幅度和稀疏性，SAPF 将稀疏扰动分解为连续幅度和二元选择因子来解决混合整数规划问题，Homotopy attack 利用加速近端梯度联合处理稀疏性和扰动边界。然而，这些方法往往资源消耗大。
3. 掩码引导的对抗攻击：通过从语义信息导出的掩码引导来增强扰动生成。Dong等人在图像注意力图的最显著区域生成超像素级扰动，FIA 根据聚合梯度掩码中的正负值分别减少和增加扰动的重要特征，Zhang等人采用 CAM 掩码定义加权余弦相似性来生成跨不同域的可转移扰动，Wei等人通过可学习掩码丢弃特定模型的补丁以减少扰动训练中的过拟合。但这些方法生成的是密集或局部扰动，并非稀疏扰动。
4. 基于生成器的对抗攻击：GAP 利用生成器结构学习从原始图像到对抗样本的映射关系，Mopuri 等人提出利用特定类特征生成通用对抗扰动的生成模型，GreedyFool 采用基于 GAN 的框架生成失真图以创建稀疏扰动，TSAA 利用生成器创建稀疏扰动并专注于提升稀疏攻击的转移性。不过，这些方法普遍缺乏对扰动位置的结构化约束，可能导致转移性下降。

---

方法-Methodology

Preliminary

这部分内容主要介绍了符号表示、稀疏对抗攻击的基本形式、局限性，以及可转移稀疏对抗攻击（TSAA）的相关内容，具体如下：

1. 符号定义与基本概念：定义 $x$ 为原始图像，$y$ 为其真实类别标签，$f(x{)}_k$ 是威胁模型 $f$ 对类别 $k$ 的输出 logit 值，原始良性图像满足 $\arg {\max }_{k}f(x{)}_k=y$. 添加扰动 $\delta$ 生成对抗样本 $x_{adv}=x+\delta$，需满足 $\arg {\max }_{k}f(x_{adv}{)}_k\ne y$. 稀疏对抗攻击通过最小化扰动 $\delta$ 的 ${\ell }_0$ 损失，在保证扰动稀疏且不可感知的同时实现攻击目的，其约束条件包括 $\Vert \delta {\Vert }_{\infty }<ϵ$，目标性攻击与非目标性攻击的约束条件有所不同。
2. 稀疏对抗攻击的局限：由于稀疏对抗样本高度依赖威胁模型，在目标模型上的转移性较差。
3. TSAA介绍：生成模型可提升稀疏对抗样本的迁移性，TSAA 将扰动表示为 $\delta =r\odot m$，其中 $r$ 和 $m$ 分别表示扰动的幅度和位置，由生成网络 $G$（包含编码器 $E$ 和解码器 $D_1$、$D_2$ ）生成。其数学公式为在满足一定约束条件下，最小化包含对抗损失和稀疏性约束的目标函数，对抗损失 $L_{adv}$ 根据攻击类型有不同的计算方式。在实际攻击中，可利用预训练的生成器 $G$ 快速生成对抗样本 $x_{adv}=x+G(x)$.

可迁移结构稀疏攻击-Transferable Structural Sparse Attack

这部分主要提出了可迁移结构稀疏攻击方法，在 TSAA 基础上进行改进，通过引入新的优化问题和结构稀疏性约束，增强对抗攻击在不同目标模型间的迁移性，具体内容如下：

1. TSAA的局限性：TSAA 虽然提高了稀疏攻击在目标模型上的迁移性，但仅依赖基于 ${\ell }_1$ 范数的像素级稀疏性来训练生成网络 $G$，没有考虑结构化语义信息，导致不同代理模型生成的扰动模式差异大，影响了迁移性。
2. 可转移结构稀疏攻击的优化问题：为进一步提升跨不同目标模型的迁移性，文章提出优化问题，在原有的对抗损失基础上增加了结构稀疏性诱导惩罚项 ${\mathcal{L}}_{sparse}(m)$ 来约束扰动位置 $m$，其表达式为 ${\mathcal{L}}_{sparse}(m)={\lambda }_1\Vert m{\Vert }_1+{\lambda }_2\Vert m{\Vert }_{21}^{\mathcal{G}}$. 其中，${\ell }_1$ 范数用于控制像素级的细粒度稀疏性，组 ${\ell }_{21}$ 范数控制组级的粗粒度稀疏性。通过将 $m\in {0,1}^{W\times H}$ 划分为 $P\times Q$ 个大小相等且不重叠的组（预定义步长为 $S$），组 ${\ell }_{21}$ 范数可重写为 $\Vert m{\Vert }_{21}^G={\sum }_{p=1}^P{\sum }_{q=1}^Q{\Vert m_{G_{p,q}}\Vert }_2$，$m_{G_{p,q}}$ 表示第 $(p,q)$ 组中的元素向量。
3. 问题的松弛形式：为解耦两个稀疏性诱导惩罚项之间的优化，引入辅助变量 $P$，并将组 ${\ell }_{21}$ 范数替换为组 ${\ell }_{20}$ 范数以实现精确 $k$ 稀疏性，降低微调稀疏性超参数的计算成本。此时，原问题转化为新的优化形式，结构稀疏性 $m$ 由生成网络 $G$ 和量化网络 $Q$ 共同生成，后续还会引入平滑损失来约束两者关系，此时稀疏惩罚项简化为仅 ${\lambda }_1\Vert m{\Vert }_1$.
   
   图2. 我们所提出的可转移结构稀疏攻击方法的整体框架（上方：生成网络G；下方：掩码量化网络Q）。

精确组稀疏训练-Exact Group Sparsity Training

该部分主要介绍了精确组稀疏训练方法，通过重新改写问题和定义相关概念，实现了在像素级和组级学习结构稀疏性，增强了对抗扰动的转移性，具体内容如下：

1. 精确 $k$ 组稀疏性：为有效求解优化问题，满足基于组 ${\ell }_{20}$ 范数的等式约束，将原问题改写为新的形式。引入组掩码 $c_{G_{p,q}}$，它取值为 $0_{S^2},1_{S^2}$，用于指示 ${\rho }_{G_{p,q}}$ 中 $S^2$ 个元素是否被选择。通过稀疏训练，从总共 $P\times Q$ 个组中找出 $k$ 个最重要的组，对其余组进行修剪，使得 $\Vert \hat{\rho }{\Vert }_{20}^G=k$（$\hat{\rho }=c\odot \rho$ ），以此实现精确 $k$ 组稀疏性。
2. 组特征重要性：为将分类相关语义融入稀疏训练，基于类激活图（如Grad - CAM）提出组特征重要性。对于代理模型选定的中间层，先计算特征重要性 $FI$ ，公式为 $FI=P_O({\sum }_d({\sum }_i{\sum }_{j}Gra{d}_{i,j}^{(d)})\cdot Fea{t}^{(d)})$，其中 $Gra{d}^{(d)}$ 和 $Fea{t}^{(d)}$ 分别表示第 $d$ 个通道的梯度和特征矩阵，$P_O(\cdot )$ 用于将变量上采样到原始空间。在此基础上，定义相对于 $(p,q)$ - 组的组特征重要性 $GFI$ 为 $GF{I}_{p,q}={\Vert F{I}_{{\mathcal{G}}_{p,q}}\Vert }_2$，该值表示每个组 ${\mathcal{G}}_{p,q}$ 的聚合分类相关重要性。通过对 $GFI$ 进行排序，获取前 $k$ 个最大值的索引集 $K=top(GFI,k)$，若 $(p,q)\in K$，则 $c_{{\mathcal{G}}_{p,q}}=1_{S^2}$，否则 $c_{{\mathcal{G}}_{p,q}}=0_{S^2}$。在训练阶段，$GFI$ 引导生成器学习结构化扰动位置以提升转移性；在测试阶段，它将扰动限制在与其他方法一致的稀疏度水平。

掩码量化网络-Masked Quantization Network

该部分主要介绍了掩码量化网络，通过将精确 $k$ 组稀疏性集成到网络中，生成结构稀疏扰动并稳定训练过程，具体内容如下：

1. 掩码量化：标准量化网络只能生成像素级稀疏的扰动，为解决这一问题，文章将精确 $k$ 组稀疏性集成到掩码量化网络 $Q$ 中。基于伯努利分布 $B(p)$ 和组掩码 $c$，网络 $Q$ 生成结构稀疏位置 $m$. 对于解码器 $D_2$的输出 $\rho$，其每个元素 ${\rho }_{ij}$ 依据伯努利分布随机采样进行量化，当采样结果 $X=1$ 时，$m_{ij}={\rho }_{ij}$；当 $X=0$ 时，$m_{ij}$ 由掩码量化函数 $q(\cdot )$ 确定，即当 ${\rho }_{ij}\cdot c_{ij}\le \tau$ 时，$m_{ij}=0$，当 ${\rho }_{ij}\cdot c_{ij}>\tau$ 时，$m_{ij}=1$，其中 $\tau$ 为阈值。这样，在每个训练轮次中，约 $(100\cdot p)\%$ 的元素会通过反向传播进行更新。
2. 掩码平滑损失：由于 $m$ 中部分元素已被量化为 0 或 1，可将其视为伪标签来引导 $\rho$ 的学习。为有效生成结构稀疏性，引入掩码平滑损失，使变量 $\rho$ 和 $m$ 接近。掩码平滑损失有硬损失和软损失两种形式，硬损失 ${\mathcal{L}}_{smooth}^{(hard)}=\Vert c\odot \rho -c\odot m{\Vert }_2^2$ 可在组掩码 $c$ 内学习结构稀疏位置，软损失 ${\mathcal{L}}_{smooth}^{(soft)}=\Vert \rho -c\odot m{\Vert }_2^2$ 可在组掩码 $c$ 外学习结构稀疏位置。此外，该平滑损失还能保证优化过程的收敛，起到正则化的作用，最小化原变量 $m$ 和辅助变量 $\rho$ 之间的差异。

多阶段优化算法-Multi-Stage Optimization Algorithm

该部分主要介绍了多阶段优化算法，通过定义整体损失函数，并采用分阶段优化的策略，解决了结构稀疏性在生成模型中难以有效优化的问题，具体内容如下：

1. 整体损失函数：为将掩码量化网络与精确组稀疏训练相结合，定义了整体损失函数 $\mathcal{L}={\mathcal{L}}_{adv}+{\lambda }_1{\mathcal{L}}_{sparse}+{\lambda }_2{\mathcal{L}}_{smooth}$. 其中，${\mathcal{L}}_{smooth}$ 可以是硬掩码平滑损失或软掩码平滑损失，${\lambda }_1$ 和 ${\lambda }_2$ 是超参数，用于平衡不同损失之间的相对重要性，并调整稀疏性水平。${\mathcal{L}}_{adv}$ 是对抗损失，衡量生成的对抗样本与真实标签之间的差异；${\lambda }_1{\mathcal{L}}_{sparse}$ 用于约束扰动位置的稀疏性；${\lambda }_2{\mathcal{L}}_{smooth}$ 用于使变量 $\rho$ 和 $m$ 接近，保证优化的收敛性。
2. 多阶段优化策略：在初步实验中发现，结构稀疏性在生成模型中难以最小化。如果 ${\lambda }_1$ 设置较大，经过几次训练迭代后，扰动位置的 ${\ell }_1$ 损失会迅速变为零，这是由于不同损失值之间的不平衡导致的；而较小的 ${\lambda }_1$ 又无法生成稀疏扰动，也不能达到与其他方法一致的期望稀疏度水平。
   为解决这一不稳定的训练问题，文章提出多阶段优化算法。在训练的第一阶段，仅在组掩码的温和引导下鼓励模型搜索最脆弱的位置，不对扰动位置施加任何稀疏性约束，即 ${\lambda }_1^{(1)}=0$ 且 ${\lambda }_2^{(1)}>0$；在第二阶段，在更强的组掩码引导下，使用 ${\ell }_1$ 稀疏性约束来生成更稀疏的对抗扰动，即 ${\lambda }_1^{(2)}>0$ 且 ${\lambda }_2^{(2)}>0$（${\lambda }_2^{(2)}\gg {\lambda }_2^{(1)}$）。算法1总结了整个可转移结构稀疏攻击的多阶段优化过程，包括初始化生成网络 $G$，在不同阶段设置不同的超参数进行多次迭代训练，最后返回生成网络 $G$ 的所有参数。
   

---

实验-Experiment

实验设置-Experimental Setting

这部分主要介绍了实验的设置，包括实验所采用的模型、数据集、评估指标、对比方法以及具体的实现细节，确保实验的科学性和结果的可靠性，具体内容如下：

1. 实验模型设置：选择Inception - V3（IncV3）和Resnet50（Res50）作为生成对抗样本时的代理模型，利用它们学习到的映射关系，从原始图像快速生成对应的对抗样本。其中，IncV3 模型要求输入图像裁剪为 299×299，Res50 要求为 224×224。同时，选用 VGG16 和 Densenet161（Dense161）作为目标模型，用于测试对抗样本的攻击效果。
2. 数据集选择：使用广泛应用的 Imagenet 数据集作为训练集。为保证与其他稀疏攻击方法对比的公平性，采用与 TSAA 相同的测试集，即从 Imagenet 数据集的测试集中随机选取 5000 张图像。
3. 评估指标确定：通过测试集中所有对抗样本的平均扰动率来衡量稀疏性。为评估对抗扰动的转移性，采用所有模型上的平均攻击成功率（ASR）作为指标，实验结果均以百分比（%）表示。
4. 对比方法选择：挑选了四种标准的稀疏攻击方法进行对比，分别是 $PG{D}_0$、SparseFool、GreedyFool 和 TSAA。使用这些方法的官方实现，并根据实验需求对其进行微调，使其满足实验设定的稀疏性要求。
5. 实现细节说明：所有实验均基于PyTorch框架，在NVIDIA V100 Tensor Core GPU上进行。对于 C&W 损失，设置 $\kappa =0$ 和二值化阈值 $\tau =0.5$. 针对不同的代理模型，优化组稀疏性的粒度（即步长S），IncV3 的步长优化为 13×13，Res50 的步长优化为 8×8。为解决训练收敛问题，根据扰动大小调整伯努利分布概率 $p$. 通过初步探索性实验，确定选择最有效 $k$ 值为0.6。此外，还对稀疏性超参数 ${\lambda }_1$ 和 ${\lambda }_2$ 进行调整，以适应不同的稀疏性水平。

和SOTA方法比较-Comparison with State-of-the-Art Methods

该部分主要将本文提出的方法 EGS - TSSA 与当前最先进的方法进行对比，从不同 ${\ell }_{\infty }$ 约束下的攻击成功率、扰动模式以及推理速度等方面进行评估，验证了EGS - TSSA在对抗攻击转移性等方面的优势，具体内容如下：

1. 不同 ${\ell }_{\infty }$ 约束下的攻击成功率对比：在不同 ${\ell }_{\infty }$ 约束条件下，评估了对抗扰动的转移性，实验结果展示了白盒和黑盒攻击在不同稀疏性水平下的情况。以 Imagenet 数据集为例，当 ${\ell }_{\infty }=10$ 时，使用 IncV3 作为代理模型，EGS - TSSA 在软约束和硬约束下的平均攻击成功率（ASR）均优于 TSAA，且软约束下 ASR 更高；以 Res50 为代理模型时，EGS - TSSA 的转移性提升也很明显，但在对 Dense161进行黑盒攻击时，其性能不如 TSAA，这是由于 Res50 原始扰动生成模式的改变使其更适合攻击 VGG16。当 ${\ell }_{\infty }=255$ 时，EGS - TSSA 的转移性依然超过TSAA。
   
   表1. 在 ${\ell }_{\infty }=10$ 的扰动幅度约束下，ImageNet数据集上无目标攻击转移性的比较。“*”表示白盒设置，“Average”和“Averagebb”分别表示所有模型的平均攻击成功率（ASR）以及所有黑盒模型的平均攻击成功率（ASR）。
   
   表2. 在 ${\ell }_{\infty }=255$ 的扰动幅度约束下，ImageNet数据集上无目标攻击转移性的比较。“*”表示白盒设置，“Average”和“Averagebb”分别表示所有模型的平均攻击成功率（ASR）以及所有黑盒模型的平均攻击成功率（ASR）。
2. 扰动模式对比：通过对比不同稀疏对抗攻击方法生成的扰动模式发现，EGS - TSSA生成的扰动更具结构化，且更集中于分类目标。与其他方法相比，其能使扰动更有效地作用于关键区域，这有助于提升攻击效果。
   
   图3. 不同稀疏对抗攻击方法的扰动模式对比。与其他方法相比，我们的精确组稀疏可转移结构稀疏攻击（EGS - TSSA）方法生成的扰动明显更加集中，且结构更规整。
3. 推理速度对比：在 IncV3 和 Res50 模型上进行推理速度对比，结果显示从低到高依次为 GreedyFool、PGD${}_0$、SparseFool、EGS - TSSA、TSAA。EGS - TSSA 的推理速度与 TSAA 相近，在实际应用中具有一定优势。

应用结构稀疏攻击-Practical Structural Sparse Attack

这部分主要展示了所提方法在多种实际攻击任务中的有效性，通过对不同目标的攻击实验，对比了本文方法 EGS - TSSA 与 TSAA 的性能，具体内容如下：

1. 对目标标签的攻击：沿用TSAA中 ${\ell }_{\infty }=255$ 的设置，选取 “bubble”（ID：971）作为目标类别进行目标性攻击对比。实验结果表明，以 IncV3 和 Res50 作为代理模型时，EGS - TSSA 的目标性攻击转移性最佳，大幅提高了平均攻击成功率（ASR），展现出该方法在针对特定目标攻击时的优势。
   
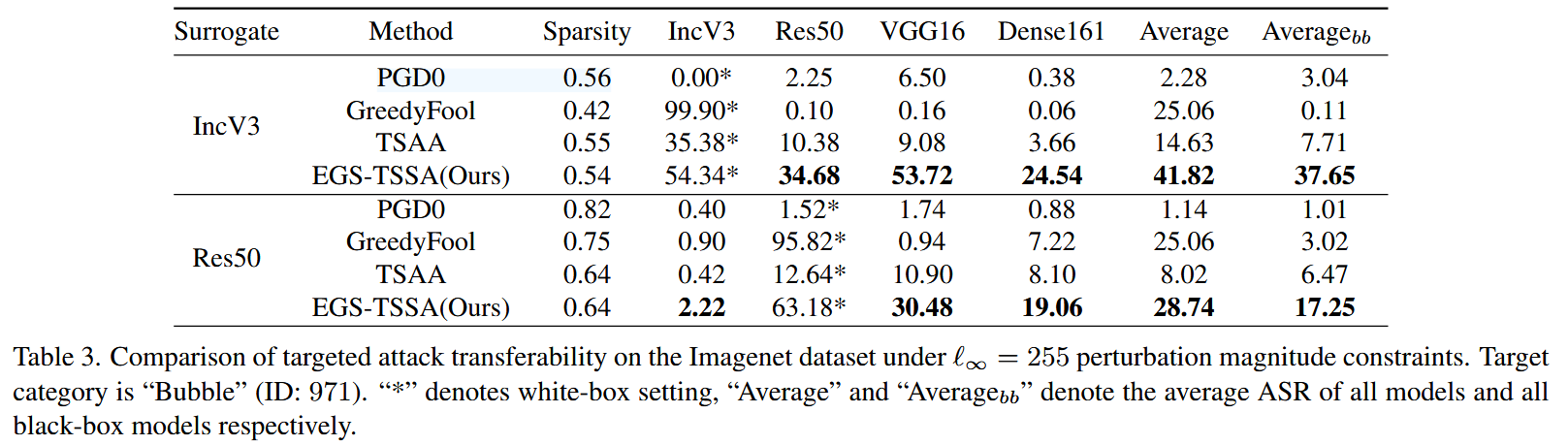
   表3. 在 ${\ell }_{\infty }=255$ 的扰动幅度约束下，在ImageNet数据集上针对性攻击转移性的比较。目标类别是“气泡”（编号：971）。“*”表示白盒设置，“Average”和“Averagebb”分别表示所有模型的平均攻击成功率（ASR）和所有黑盒模型的平均攻击成功率（ASR）。
2. 对ViT的攻击：进一步评估了基于白盒CNN生成的对抗样本对黑盒视觉 Transformer（ViT）模型的攻击性能。使用 IncV3 和 Res50 作为代理模型，在 ${\ell }_{\infty }=255$ 的非目标性攻击设置下，直接利用训练权重进行攻击，结果显示 TSAA 和 EGS - TSSA 的转移性均显著降低。分析认为，这是因为基于 CNN 模型生成的高转移性扰动结构较强且连续，而 ViT 将图像划分为多个补丁，破坏了这种结构。但即便如此，EGS - TSSA 在攻击 ViT 模型时，平均 ASR 仍高于 TSAA，体现出其相对优势。
   
   表4. 各种攻击在视觉Transformer（ViT）模型上的转移性。所有针对ViT模型的实验的评估指标均为攻击成功率（ASR）。
3. 对语义分割的攻击：在非目标性攻击且 ${\ell }_{\infty }=255$ 的设置下，利用预训练的生成器对语义分割任务进行攻击，使用 VOC2012 数据集的验证集作为测试数据，以平均交并比（mIoU）作为评估指标。结果表明，结构稀疏攻击会导致模型分割性能显著下降，且 EGS - TSSA 与 TSAA 在该任务上均使模型性能降低，但未明确表明两者的优劣差异。
   
   表5. 语义分割任务中各种攻击的性能表现。所有语义分割实验的评估指标均为平均交并比（mIoU）。
4. 对目标检测的攻击：利用在非目标性攻击（${\ell }_{\infty }=255$）下训练的生成器攻击目标检测模型，以 COCO 数据集的验证集为测试数据，通过平均精度（AP）和平均召回率（AR）（在 $IoU=[0.5:0.95]$ 上平均）评估模型检测性能。结果显示，EGS - TSSA的结构稀疏扰动使模型检测性能下降更显著，相比 TSAA 在降低目标检测性能方面表现更优，进一步验证了该方法在攻击目标检测模型时的有效性。
   
   表6. 目标检测任务中各种攻击的性能表现。与可转移稀疏对抗攻击（TSAA）相比，我们提出的精确组稀疏可转移结构稀疏攻击（EGS - TSSA）使得目标检测性能出现了更为显著的下降。平均精度（AP）和平均召回率（AR）分别表示平均精确度和平均召回率，所有实验结果均是在交并比（$IoU$）处于 $[0.5:0.95]$ 范围内时取的平均值。

分析稀疏扰动的性质-Analyze the Property of Sparse Perturbation

该部分从稀疏扰动的分布和有效性两个方面进行分析，验证了本文方法 EGS - TSSA 生成的稀疏扰动的特性，进一步说明了该方法的优势，具体内容如下：

1. 稀疏扰动的分布：利用增强的 top - k 模块，依据组特征重要性（GFI）将预定义的 $P\times Q$ 个组划分为10个区域。通过实验对比发现，应用 GFI 引导约束后，IncV3 模型的扰动更集中在分类重要区域；Res50 模型的扰动分布与之前相比发生了明显变化，也更多地集中在分类特征重要的区域。这使得 IncV3 和 Res50 模型的扰动分布在一定程度上实现了统一，表明 EGS - TSSA 能够引导扰动集中在关键区域。
   
   图4. 扰动分布的对比分析。利用选定的10个区域，我们统计了由EGS - TSSA和TSAA生成的扰动情况。很明显，我们的方法使两种代理模型的扰动分布趋于一致。
2. 稀疏扰动的有效性：进一步分析不同区域扰动的攻击成功率（ASR），结果显示由 GFI 约束产生的扰动，越靠近特征重要区域，对整体ASR的贡献越大。从实验结果图中可以看出，EGS - TSSA 方法能使不同模型的扰动更集中在与分类相关的重要区域，这意味着该方法生成的扰动在重要区域具有更高的攻击效率，从而提升了整体的攻击性能。
   
   图5. 各区域扰动的攻击成功率（ASR）。针对图4中每个区域的扰动计算了攻击成功率，结果表明我们的方法在特征重要区域生成的扰动具有更高的攻击成功率。
   
   图6. 不同方法生成的扰动分布。“0 - 0.6”表示基于组特征重要性（GFI）选择扰动区域中最重要的60%，“0.6 - 1”表示剩余的40%区域，“0.4 - 1”表示选择不太重要的60%区域。纵坐标显示了相应区域中扰动的百分比。

---

结论-Conclusion

这部分总结了研究工作，强调了创新点、实现方式及实验验证结果，具体如下：

1. 研究成果：提出一种生成结构稀疏扰动的新方法，该方法增强了扰动的转移性和不可感知性。与传统稀疏攻击不同，更注重扰动位置，以此优化稀疏扰动的结构。
2. 实现方式：通过精确组稀疏训练实现结构稀疏性约束，在学习像素级和组级稀疏性的同时，让扰动更自然地融入分类相关特征。引入掩码量化网络，将精确k组稀疏性集成其中，生成结构稀疏扰动并稳定训练。提出多阶段优化算法，解决生成模型中结构稀疏性难以最小化的问题，确保扰动位置和稀疏性受约束的同时避免扰动消失。
3. 实验验证：大量实验表明，在近似相同的稀疏度水平下，该方法在图像分类攻击中的转移性优于现有方法。在跨模型的 ViT、目标检测和语义分割攻击任务中，也取得了更高的攻击成功率，验证了方法的优越性。